无耦合交叉线高温超导准椭圆函数滤波器

张天良，周立国，羊 恺，陈 鹏，任向阳，侯方焰，杨常林(电子科技大学航空航天学院 成都 611731)



无耦合交叉线高温超导准椭圆函数滤波器

张天良，周立国，羊 恺，陈 鹏，任向阳，侯方焰，杨常林
(电子科技大学航空航天学院 成都 611731)

【摘要】提出了一种用于设计高温超导小型化准椭圆函数滤波器的新型多曲折谐振器结构，在不改变滤波器总体布局的情况下，通过优化谐振器结构来直接实现拓扑逻辑上非相邻谐振器之间的交叉耦合，引入多对传输零点以提高滤波器的带外抑制。既能利于实现滤波器的小型化，也能避免耦合交叉线对加工工艺的特殊要求。利用自拟耦合矩阵，在31.5 mm×15.6 mm，厚度为0.5 mm、介电常数为24的双面YBCO/LaAlO3/YBCO高温超导薄膜上，设计制作了具有3对传输零点的12阶CDMA 2 000高温超导滤波器。在77 K时测得滤波器的中心频率为830 MHz，带宽为10 MHz，带边滚降大于45 dB/MHz，带内插入损耗最优值小于0.4 dB，回波损耗整体优于−11.3 dB，加工测试结果与仿真设计结果基本吻合。

关 键 词滤波器; 高温超导; 小型化; 多曲折谐振器; 传输零点

High Temperature Superconducting Quasi-Elliptic Function Filter Without Cross-Coupled Line

ZHANG Tian-liang, ZHOU Li-guo, YANG Kai, CHEN Peng, REN Xiang-yang, HOU Fang-yan, and YANG Chang-lin
(School of Astronautics and Aeronautics, University of Electronic Science and Technology of China Chengdu 611731)

Abstract This paper presents a group of improved multi-zigzag resonators to design high temperature superconducting (HTS) miniaturization quasi-elliptic filter. With a little change of the filter’s layout, cross-couplings between non-adjacent resonators in topology logic are directly achieved without any cross-coupling line by optimizing the resonator’s structure, and multi-pairs of transmission zeros are introduced to improve out-of-band rejection of filter, which are not only beneficial for filter’s miniaturization, but also avoids the high processing-technical requirement caused by cross-line coupling. By using a self-synthesized coupling matrix, a 12th-order HTS filter is designed with 3 pairs of transmission zeros on a double-sided YBCO/LaAlO3/YBCO high temperature superconducting thin film whose size is 31.5 mm×15.6 mm, thickness is 0.5 mm, and dielectric constant is 24. At 77 K, the filter’s tested center frequency is 830 MHz with a bandwidth of 10 MHz, a band edge roll-off more than 45 dB/MHz, a insert losing less than 0.4 dB and a return losing better than −11.3 dB.

Key words filter; high temperature superconducting; miniaturization; multi-zigzag resonator; transmission zero

当前，移动通信频谱资源变得越来越紧张，通信系统对滤波器的性能要求也越来越高。采用高温超导薄膜设计制作的微带滤波器具有极低的插入损耗、优异的频率选择特性等优点，已被广泛应用于各类通信系统中[1-4]。高温超导滤波器设计时，为了获得更为优异的带外抑制特性，除了尽可能采用小型化单元谐振电路以增加级数外，还广泛采用准椭圆函数响应的电路结构形式[3-11]。

对于高温超导滤波器系统而言，一般是采用制冷机来提供低温环境，为了减小制冷机的热负载，缩短制冷时间，提高制冷效率，要求高温超导器件尺寸越小越好。因此，尽可能采用小型化谐振器并在拓扑逻辑上非相邻谐振器之间增加交叉耦合引入传输零点是很常用的方法，既能减小滤波器的尺寸又能提高滤波器的带外抑制。CQ(cascaded quadruplet)结构是引入传输零点的一种比较成熟的结构，每一组CQ单元可以引入一对传输零点[8-11]。但如果用耦合交叉线来实现非相邻谐振器之间的交叉耦合，会使电路对光刻工艺要求相对较高。为此，本文提出新的改进型多曲折谐振器结构，并合理布局谐振器的相对位置来构造CQ单元，引入多对传输零点来提高滤波器带外抑制，同时无需使用耦合交叉线可减小对光刻加工工艺的要求。最后，采用多曲折谐振器并结合自行综合的耦合矩阵，设计制作了用于CDMA 2 000的12阶高温超导滤波器。

1 12阶准椭圆函数滤波器耦合系数的综合

本文设计的滤波器中心频率为830 MHz，带宽为10 MHz。结合自行研究的滤波器耦合系数综合方法[12]，综合了一组12阶滤波器的耦合系数，详见表1。其中mij代表第i级与第j级谐振器间的耦合系数，对应的拓扑结构见图1，图中每一个圆圈代表一个谐振器，圆圈内数字代表谐振器的编号，实线代表相邻谐振器之间的耦合，虚线代表非相邻谐振器之间的交叉耦合，S和L分别代表输入和输出。

表1　各谐振器间的耦合系数

利用表1的耦合系数，可以获得12阶准椭圆函数滤波器的理想频率响应曲线，如图2所示。

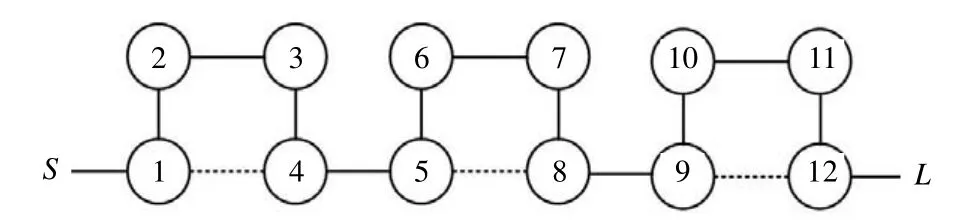
图1　12阶准椭圆函数滤波器拓扑结构

图2　12阶准椭圆函数滤波器的理想频率响应曲线

2 多曲折线半波长谐振器

在设计微带线滤波器时，常采用半波长谐振器作为基本谐振单元。为了尽可能减小器件尺寸，已经构造出了多种形式的小型化半波长微带线谐振器，图3所示是几种常见且使用比较灵活的多曲折线谐振器[9,11,13]。

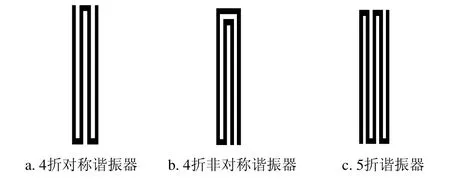
图3　几种常见的谐振器

本文将图3a所示的谐振器变形为图4a所示的谐振器；将图3b所示的谐振器变形为图4b所示的谐振器。然后利用图4a、图4b和图3c的3种谐振器构造出图5所示的两种CQ单元，图5中字母代表谐振器编号。

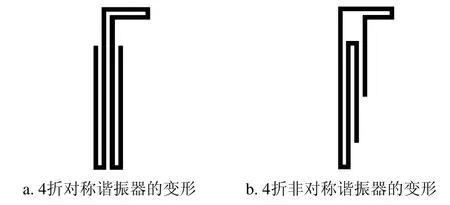
图4　变形后的谐振器

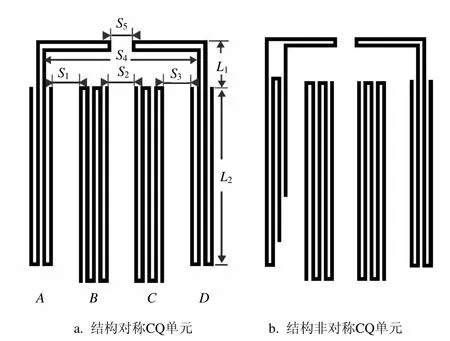
图5　两种CQ单元

图5a中，谐振器A与谐振器B之间、谐振器B与谐振器C之间、谐振器C与谐振器D之间均为电容耦合。在设计A与D之间的耦合时，充分利用A和D的中部区域，保证谐振器之间距离S5在满足工艺最低缝隙宽度条件下，获取较大的耦合[13]。而且此时A与D之间的耦合为磁场耦合，正好和B与C之间电场耦合的耦合极性相反，从而可产生一对传输零点。此外，图5a中谐振器A与谐振器C(谐振器B与谐振器D)之间的耦合很弱。这样，既避免了使用耦合交叉线来实现A与D之间的交叉耦合，也避免了CQ单元中不必要的交叉耦合。同时，考虑到本文设计的滤波器相对带宽较小，如果采用输入、输出传输线与谐振器直接相连的方式来获取外耦合，则需要尽可能把最边侧的谐振器中部区域放在最外侧，因此在保证各谐振器之间耦合属性不变的前提下，将图5a中外侧的一个谐振器替换为图4b所示的谐振器，并构造出图5b的CQ单元。

3 高温超导滤波器的仿真设计

本文采用表1中各级谐振器间的耦合系数指导滤波器物理电路的设计，采用介电常数为24，厚度为0.5 mm的LaAlO3基片。为了设计方便，首先分别对3个CQ谐振单元进行单独设计，然后再进行各个CQ单元之间的耦合设计。

在设计图5a所示的CQ单元时，所有谐振器线宽和谐振器内部缝隙宽度均设置为0.1 mm。首先通过全波仿真软件仿真获得图6a所示S2与kBC之间的关系，S2为图5a中谐振器B与谐振器C之间的耦合间距，kBC为谐振器B与谐振器C之间的耦合系数。再根据表1中对应的耦合系数即可确定S2的初值SBC，并保持不变。然后把图5a中谐振器端头到顶部的距离L1设置为2.4 mm，设置为较大值的目的是尽可能避免谐振器A与C(B与D)之间不必要的交叉耦合。再将谐振器A和B的最右侧对齐，考虑到谐振器A与B之间和谐振器B与C之间的耦合系数比较接近，因此在把谐振器A与谐振器B之间的间距S1设置为和前述SBC相等的值，进行A与B之间的耦合仿真，S1与kAB的关系如图6b所示，kAB为图5a中谐振器A与B之间的耦合系数。仿真过程中谐振器A和B虽然结构不同，但需要保证它们的谐振频率相同。同理，根据表1中对应的耦合系数可确定S1的初值SAB以及谐振器C与D之间的间距S3的初值SCD。在S1、S2、S3和L1的初值都确定后，谐振器A和D的相对位置就已经确定下来，即S4已经确定。然后通过改变谐振器A与D之间的耦合距离S5来改变它们之间的耦合系数kAD，S5与耦合系数kAD之间的关系如图6c所示。在改变S5的时候不能改变S4，只能通过同步调节谐振器中L2的值来保持谐振器的谐振频率不变。

当完成所有CQ单元后，即可仿真各个CQ单元之间的耦合距离，从而完成整个电路初值的搭建。通过微调各个谐振器的尺寸及各耦合距离S的大小，优化后最终完成整个高温超导滤波器平面电路设计，如图7所示，电路尺寸为31.5 mm×15.6 mm。在进行电路优化时，尽可能保持所有谐振器的顶端位置不变，只调节下端的位置以降低微调的复杂性，也便于降低电路后期封装的难度。全波分析得到的频率响应曲线如图8所示。和图2对比可以得出，滤波器的仿真设计值与理论值吻合较好。

图7　高温超导滤波器平面拓扑结构

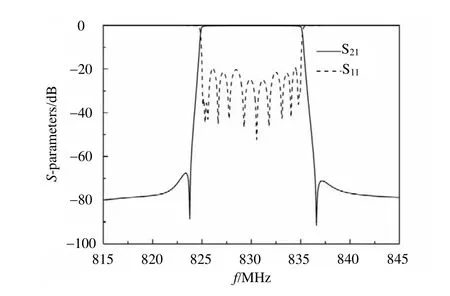
图8　高温超导小型化准椭圆函数滤波器仿真结果

4 高温超导滤波器的制作与测试

本文采用YBCO/LaAlO3/YBCO高温超导薄膜，厚度为0.5 mm，介电常数为24，加工的实物如图9所示。高温超导滤波器采用半导体平面精细加工技术—离子束刻蚀工艺制作。采用矢量网络分析仪Agilent 8720ET对设计制作完成的滤波器进行测试，最终的测试结果曲线如图10所示。在77 K时，超导滤波器实测中心频率为830 MHz，带宽约10 MHz，带边滚降大于45 dB/MHz，通带内的插损最优值小于0.4 dB，通带内中心区域60%范围内回波损耗优于−12.5 dB，但通带两端小区域回波损耗不够理想，最差值为−11.3 dB，造成部分频点的插损较大，通带内最大插损值在825.43 MHz附近为1.23 dB。

图9　高温超导准椭圆函数滤波器实物照片

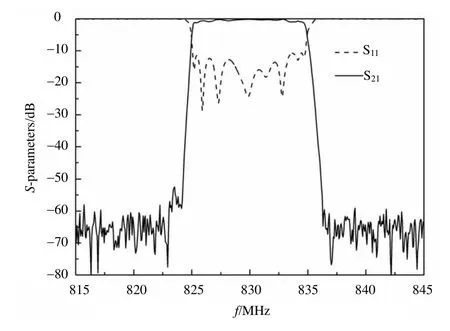
图10　高温超导小型化准椭圆函数滤波器测试结果

5 结 束 语

本文在不引入耦合交叉线的前提下，通过合理改变谐振器的结构来直接实现非相邻谐振器之间的交叉耦合，引入3对传输零点提高了滤波器的带外抑制。既实现了滤波器的小型化设计，也避免了使用耦合交叉线，降低了电路对加工工艺的要求。利用该方法完成了含有3个CQ单元的高温超导滤波器仿真设计和加工，测试结果与理论响应基本符合。这种通过合理改变谐振器结构引入非相邻谐振器之间交叉耦合的方法，为下一步设计更高阶小型化高选择性准椭圆函数滤波器提供了保障。

参 考 文 献

[1] SUN L, HE Y. Research progress of high temperature superconducting filter in China[J]. IEEE Transactions on Applied Superconductivity, 2014, 24(5): 1-8.

[2] SAITO A, TESHIMA H, OBARA H, et al. Design and performance of transmit filters using HTS bulk resonators for IMT-advanced applications[J]. IEEE Transactions on Applied Superconductivity, 2007, 17(2): 886-889.

[3] HONG J S, LANCASTER M J, JEDAMZIK D, et al. On the performance of HTS microstrip quasi-elliptic function filters for mobile communications application[J]. IEEE Transactions on Microwave Theory and Techniques, 2000, 48(7): 1240-1246.

[4] ZHANG G, HUANG F, LANCASTER M J. Superconducting spiral filters with quasi-elliptic characteristic for radio astronomy[J]. IEEE Transactions on Microwave Theory and Techniques, 2005, 53(3): 947-951.

[5] TSUZUKI G, YE S, BERKOWITZ S. Ultra-selective 22-pole 10-transmission zero superconducting bandpass filter surpasses 50-pole Chebyshev filter[J]. IEEE Transactions on Microwave Theory and Techniques, 2002, 50(12): 2924-2929.

[6] ZUO T, YAN S, ZHAO X, et al. The design of a linear phase superconducting filter with quasi-elliptic response[J]. Superconductor Science and Technology, 2008, 21(6): 065018.

[7] ZHANG T, YANG K, ZHANG Y, et al. Parallel-coupled linear-phase superconducting filter[J]. Chinese Science Bulletin, 2014, 59(16): 1925-1928.

[8] HONG J S, MCERLEAN E P, KARYAMAPUDI B. Highorder superconducting filter with group delay equalization[C]// Microwave Symposium Digest, 2005 IEEE MTT-S International. [S.l.]: IEEE, 2005.

[9] GAO L, SUN L, LI F, et al. 8-GHz narrowband hightemperature superconducting filter with high selectivity and flat group delay[J]. IEEE Transactions on Microwave Theory and Techniques, 2009, 57(7): 1767-1773.

[10] YU T, LI C, LI F, et al. A novel quasi-elliptic HTS filter with group-delay equalization using compact quasi-lumped element resonators in VHF band[J]. IEEE Transactions on Applied Superconductivity, 2009, 19(2): 69-75.

[11] 张天良, 羊恺, 孔根升, 等. 高温超导小型化交叉线自均衡线性相位滤波器[J]. 科学通报, 2010(15): 1453-1458. ZHANG Tian-liang, YANG Kai, KONG Gen-sheng, et al. Miniature linear-phase superconducting filter with group delay equalization[J]. Chinese Sci Bull, 2010(15): 1453-1458.

[12] 张天良. 高性能高温超导线性相位滤波器的研究[D]. 成都: 电子科技大学, 2009. ZHANG Tian-liang. Research of HTSC linear-phase filters[D]. Chengdu: University of Electronic Science and Technology of China, 2009.

[13] HONG J S, LANCASTER M J. Couplings of microstrip square open-loop resonators for cross-coupled planar microwave filters[J]. IEEE Transactions on Microwave Theory and Techniques, 1996, 44(11): 2099-2109.

编 辑 税 红

作者简介：张天良(1976 − )，男，博士，副教授，主要从事高温超导微波电子学方面的研究.

基金项目：国家自然科学基金(61471094)

收稿日期：2015 − 04 − 16；修回日期：2015 − 09 − 22

中图分类号TN713

文献标志码A

doi:10.3969/j.issn.1001-0548.2016.01.003