基于外区抑制与马尔可夫模型的轮廓检测

闫 超，张建州，姜正茂(. 四川大学计算机学院 成都 60065；. 成都国翼电子技术有限公司 成都 60045)



基于外区抑制与马尔可夫模型的轮廓检测

闫 超1，张建州1，姜正茂2
(1. 四川大学计算机学院 成都 610065；2. 成都国翼电子技术有限公司 成都 610045)

【摘要】轮廓检测是目标识别的重要前提，为解决复杂纹理自然场景下目标轮廓难以有效检测的问题，该文提出一种新的计算方法。首先，利用旋转不变滤波器快速实现外区抑制；其次，通过集合运算整合不同抑制水平的抑制后响应，得到边缘图；最后，建立基于马尔可夫随机场的轮廓概率模型，赋予每个边缘点一个概率值，选择概率较高的边缘点即得到最终的轮廓输出。定性和定量分析表明，相对于现有算法，新算法的轮廓检测性能显著提升，并具有更好的鲁棒性。

关 键 词轮廓检测; 轮廓概率; 马尔可夫随机场; 旋转不变滤波器; 外区抑制

Contour Detection Based on Surround Inhibition and Markov Model

YAN Chao1, ZHANG Jian-zhou1, and JIANG Zheng-mao2
(1. College of Computer Science, Sichuan University Chengdu 610065; 2. Chengdu Goldwin Electronics Technology Co. LTD Chengdu 610045)

Abstract Contour detection plays an important role in object recognition. In order to detect effectively the target contour with complex textures in natural scenes, a new method of contour detection is proposed in this paper. In the algorithm, the surround inhibition is realized fastly by steerable filters; the multi-inhibited responses are integrated to form an edge map under the rules of set operations, and finally, according to the theory of Markov random field, a model of contour probability is presented to give each edge point a probability and form the output of contour by thresholding the probability map. Qualitative and quantitative analysis shows that the proposed method increases the performance signifacantly and get a better result of robustness, compared with existing methods.

Key words contour detection; contour probability; markov random field; steerable filters; surround suppression

轮廓检测广泛应用于机器视觉相关的任务中，诸如目标识别、形状分析等[1-2]。鉴于此，人们已经提出了大量的轮廓检测算法。部分算法是基于灰度差分的[3]，还有一部分则是基于机器学习[4]、模糊推理[5]和活动轮廓[6]的。尽管如此，轮廓检测仍然面临着众多困难，远未得到彻底的解决。

生理学研究[7]证实，人类视觉系统存在着外区抑制特性，它可以减弱视神经元对纹理性边缘的响应，但对独立的轮廓不起作用。文献[7]首次提出了基于外区抑制特性的仿生轮廓检测方法，其主要思想是利用两个不同尺度的高斯函数作差分得到抑制滤波器，然后对梯度幅值作卷积，再由梯度幅值减去卷积结果即获得轮廓显著图。由于上述算法存在自抑制现象，不能很好地保护弱轮廓。文献[8-10]提出一系列的改进措施，取得了明显的效果，但计算复杂度却呈指数级增长。

为满足实时性要求，文献[11]引入Hermite-Gauss函数，并给出一种统一的闭型分解框架[12]，用于实现不同阶数的旋转不变滤波器(steerable filters)。具体而言，旋转不变滤波器是一组固定基函数的线性组合，角度信息分离到组合系数中。因此，选择一组旋转不变滤波器作为外区抑制核函数时，只需要少数几个低阶基函数对图像作卷积，即可得到任意角度的外区抑制量，不仅避免了自抑制现象，且计算复杂度大大降低。不过，该算法还存在如下缺陷：1) 组合方法过于简单，导致纹理性边缘去除的不彻底，且造成部分轮廓的丢失；2) 弱轮廓保护机制不健全，由于弱轮廓长度很短，接近于噪声边缘的长度，所以根据长度判断噪声边缘，也会误判弱轮廓。

针对上述缺陷，本文提出基于集合运算的组合方式，用于整合不同抑制水平的边缘响应；同时，根据马尔可夫随机场理论建立图像的轮廓概率模型，用于去除噪声边缘和保护弱轮廓。

1 仿生轮廓计算原理

1.1 高斯梯度与外区抑制

令I( x , y )表示一幅灰度图像，其高斯梯度定义为：

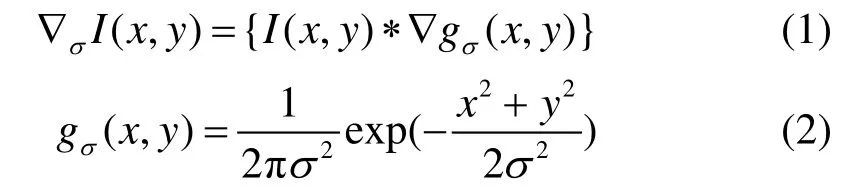
外区抑制需要用到一组不同方向的滤波器，其生成函数定义为：

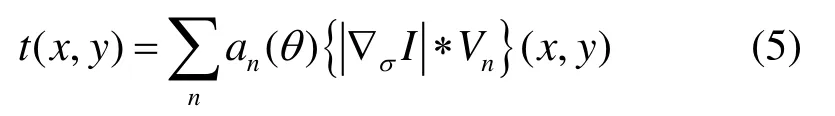
式中，θ表示梯度方向。

如图1所示，点A嵌入在纹理边缘中，其外区抑制量大于零，经过抑制后点A就会消失；而点B位于孤立边缘上，其外区抑制量等于零，经过抑制后点B保持不变。因此，外区抑制可以抑制纹理性边缘，进而保护孤立的目标轮廓。

为抑制纹理性边缘，可将梯度幅值减去抑制量，得到抑制后响应：

式中，λ称为抑制水平。由于纹理性边缘对应的抑制量一般较大，而轮廓对应的抑制量一般较小，因此，从响应中提取目标轮廓将变得较为容易。

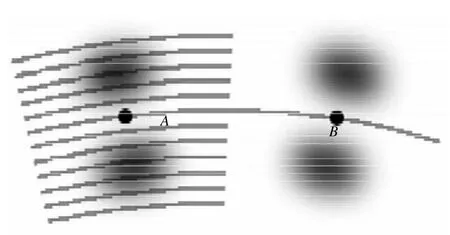
图1　纹理点和孤立点的外区抑制

1.2 非极大值抑制与迟滞阈值

式中，Card表示求取集合中非零元素的个数；M表示响应点总数。式(7)表明强轮廓像素至少包含前pM个最大响应点。取，响应中小于lT的点被看作是噪声点予以舍弃。位于两个阈值之间的弱轮廓点，如果能够连接到强轮廓上则予以保留；否则舍弃。

2 改进的仿生轮廓检测算法

由式(6)可知，当抑制水平λ取值较小时，可以较好的保护目标轮廓，但不能充分的抑制纹理性边缘；相反，当抑制水平取值较大时，虽然能够充分的抑制纹理性边缘，但目标轮廓也会有所丢失(自然场景下轮廓抑制量虽然很小，但并不等于零)。为解决上述问题，同时进一步提高轮廓检测性能，本文提出一种新的仿生轮廓检测算法。

2.1 算法框架

仿生轮廓检测算法流程图如图2所示。首先，计算图像I( x , y )的高斯梯度，并利用式(3)得到外区抑制量，通过不同抑制水平后作用于梯度幅值上，获得抑制后响应；接着，对各级响应分别进行后处理操作，得到边缘集合；然后，计算所有边缘集合的交集和并集，并以交集作为种子点在并集中选择强边缘；最后，根据马尔可夫随机场理论建立轮廓概率图，二值化概率图即得到最终的轮廓输出。

图2　仿生轮廓检测算法流程图

2.2 基于集合运算的多水平组合方法

图3显示的是不同抑制水平kλ作用下的二值图像显然，随着kλ取值的逐渐变大，轮廓点和噪声点都会有所减少，但噪声点的减少速度大于轮廓点的减少速度。对于图像点(x , y )，它在所有中出现的次数决定了它属于强边缘的程度。一般来说，孤立点或者轮廓点出现的次数要多于噪声点出现的次数。因此，可将强边缘和弱边缘分别定义为的交集和并集：

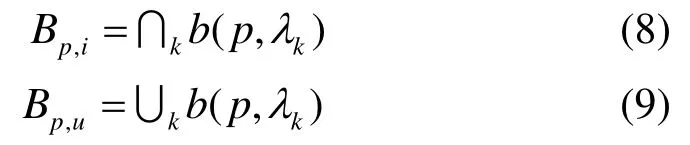
式中，交集Bp, i表示在所有中都出现的图像点集合；并集Bp, u表示在中至少出现一次的图像点集合。

图3　不同　λk取值下的?

集合运算结果如图4所示，交集包含有大量不连续的轮廓片段，而并集则同时包含有完整的轮廓和噪声边缘。为筛选出完整的轮廓并排除噪声边缘，本文以交集作为种子轮廓，然后遍历并集中所有的弱边缘Eu，如弱边缘Eu与种子轮廓有部分像素点发生重叠，则将弱边缘Eu加入到组合结果b( p , c )中，有：

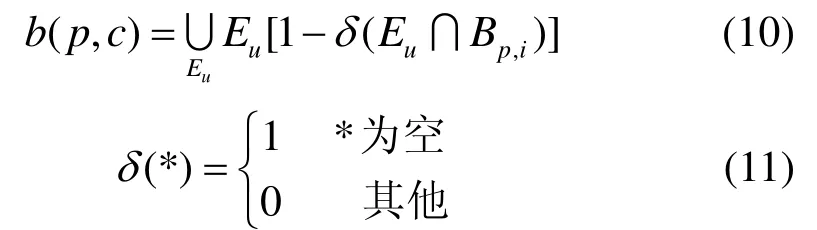
组合结果b( p , c )去除了大部分噪声边缘，同时保留了较为完整的轮廓，如图4c所示。

图4　集合运算结果

2.3 基于马尔可夫随机场的轮廓概率模型

组合结果b( p , c )中还存在着一些噪声边缘，需要进一步的排除，如图5所示，其中e1是噪声边缘，而e2是轮廓片段，它们长度一致，但位置不同。如果直接去除长度较短的边缘，那么e1和e2都会被排除，这不是人们所希望的。为保留e2，去除e1，本文提出一种基于马尔可夫随机场的轮廓判断机制。马尔可夫随机场描述了图像中像素点之间的空间相关性，设是一随机场，N =是其邻域系，若满足[14]：

则称X是关于N的马尔可夫随机场。式(12)表明随机变量Xi, j的条件概率分布只取决于它的邻域系统。将图像看作马尔可夫随机场，建立图像概率模型，则图像中任一像素点的概率(属于轮廓的可能性)都可以通过该点的邻域来进行计算。具体而言，对于b( p , c )中每条轮廓e，其轮廓概率定义为：

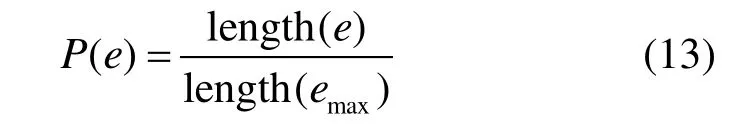
式中，emax表示b( p , c )中的最长轮廓；length(*)表示求取轮廓长度。有了轮廓概率，则轮廓点概率可定义为：

其中，

图5　伪轮廓排除示意图

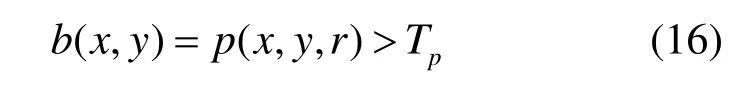
3 实验结果及分析

实验平台为CPU E6600，2 G内存，Windows7 SP1操作系统，Matlab2013a仿真软件。实验图像采用标准测试库共40幅自然图像(带有真实轮廓)。为保证实验结果对比的公平性，各算法的通用参数将采用相同的取值，其他参数则使用相关文献给出的标准值，具体设置如下：

3.1 实验结果

图6是各算法的轮廓检测结果。

图6　各算法的轮廓检测结果

图6中第1行图像由大象轮廓、山脉脊线和草木纹理组成，用于测试算法对一般性轮廓和纹理的感知能力；第2行图像中人造提篮具有很强的规则性纹理，而自然纹理则呈现出较强的随机性分布，用于测试算法对不同纹理分布的鉴别能力；第3行图像是一群拥有花斑纹理的袋狼，它们完全嵌入在草原纹理中，用于验证算法对动物自身纹理的抑制能力；第4行图像包含汽车前轮和人造路面，轮胎纹理和路面纹理都可看作是噪声纹理，可用于验证算法的降噪能力。

Canny算子[13]的检测结果如图6b所示，由于没有考虑空间点之间的互相作用，导致其无法分离出目标轮廓和纹理性边缘；DOG算子[7]的检测结果如图6c所示，由于其滤波器呈圆环型结构，会产生自抑制现象，因此，DOG算子的理论意义大于实际应用；图6d为文献[11](简称SF算法)的检测结果，由于引入了旋转不变滤波器，成功避免了自抑制现象，在抑制纹理和保护轮廓方面取得了一定的成效，但该算法的组合方法缺乏理论支撑，且没有对残留的噪声边缘作处理，所以还有一定的改进空间；图6e为本文算法的检测结果，该文算法在抑制纹理、保护弱轮廓以及去除噪声等方面都明显优于其他算法。

3.2 参数鲁棒性分析

为便于定量分析，定义轮廓检测性能[11]为：

其中：

式中，DC表示算法检测到的轮廓点集；GT表示真实轮廓点集；Card函数用于计算集合点数；dGT( x )表示轮廓点x到GT的最小欧式距离；d0用于平衡DC 和GT之间的差异(取值为2)。式(17)将F的取值限定于(0,1]区间上，F反映了算法检测出来的轮廓和真实轮廓之间的接近程度，其取值越大，则算法的轮廓检测性能就越好。算法性能采用40幅图像的平均轮廓检测性能来衡量。

算法中最为重要的两个参数分别是尺度σ和分位数p。σ决定着抑制滤波器的大小，其值越大，抑制程度也就越强。而p决定了边缘点保留的数量，其值越大，则最终轮廓点数量也会增大。

当σ保持不变，p发生变化时，各算法的平均检测性能如图7所示。当p取值趋于零时，输出的轮廓点(即DC)数量也会减少，由式(11)可知，F也会跟着变小；当p逐渐变大时，轮廓点集DC亦随之增加，则轮廓检测性能也会变大；当p过大时，轮廓点集会包含有大量的纹理性边缘，故轮廓检测性能呈现出下降趋势。从图7可知，多数情况下，本文算法的轮廓检测性能都明显优于其他3种算法。由于p接近零时，大部分弱轮廓被舍弃，而强轮廓在各个算法中都会被保留，因此，本文算法的轮廓检测性能略有下降。但在实际应用中，分位数p的这种极端取值情况一般不予考虑。

图7　分位数p对检测性能的影响

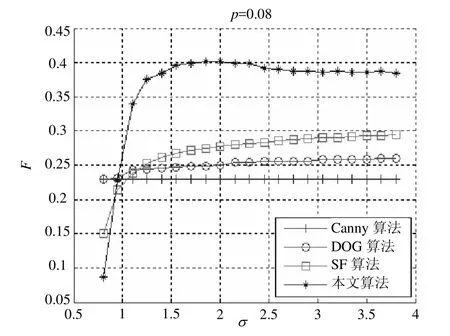
图8　尺度σ对检测性能的影响

当p保持不变，σ发生变化时，各算法的平均检测性能如图8所示，当σ取值较小时，外区抑制滤波器尺寸会变得很小，以至于无法有效抑制纹理性边缘，所以仿生轮廓检测算法的性能都呈现出快速下降的趋势；当σ>1时，抑制滤波器开始发挥作用，算法的轮廓检测性能亦随之上升。若σ取值过大，则抑制滤波器的尺寸也变大，会导致过高的时间复杂度，而性能F却提升不明显，因此σ的取值不宜过大。由图8可知，正常情况下，本文算法检测性能都高于其他3种算法。

综上所述，本文算法在轮廓检测性能方面得到了明显的提升，同时对参数也具有良好的适应性。

4 结 束 语

外区抑制现象是生物视觉系统的基本特性之一，利用这种特性可以实现纹理抑制和轮廓提取。相对于现有算法，本文提出的组合方法和轮廓概率模型很好地解决了强纹理去除和弱轮廓保护之间的矛盾。随后，大量的定性分析和定量分析都证实了本文算法的有效性。然而，生物视觉系统是极其复杂的，除了利用灰度梯度信息之外，还能够整合颜色信息与形状信息等，如何更好地模拟生物视觉系统将是下一步的研究方向。

参 考 文 献

[1] LEORDEANU M, SUKTHANKAR R, SMINCHISESCU C. Generalized boundaries from multiple image interpretations [J]. Pattern Analysis and Machine, 2014, 36(7): 1312-1324.

[2] LUI L M, ZENG Wei, YAU S T, et al. Shape analysis of planar multiply-connected objects using conformal welding[J]. Pattern Analysis and Machine, 2014, 36(7): 1384-1401.

[3] LIM D H, JANG S J. Comparison of two-sample tests for edge detection in noisy images[J]. Journal of the Royal Statistical Society, 2002, 51(1): 21-30.

[4] MARTIN D R, FOWLKES C, MALIK J. Learning to detect natural image boundaries using local brightness, color, and texture cues[J]. Pattern Analysis and Machine Intelligence, 2004, 26(5): 530-549.

[5] 沈志熙, 代东林, 赵凯. 基于多特征分步模糊推理的边缘检测算法[J]. 电子科技大学学报, 2014, 43(3): 381-387. SHEN Zhi-xi, DAI Dong-lin, ZHAO Kai. Edge detection based on multi-features and step-by-step fuzzy inference[J]. Journal of University of Electronic Science and Technology of China , 2014, 43(3): 381-387.

[6] LI H, YEZZI A J. Local or global minima: Flexible dualfront active contours[J]. Pattern Analysis and Machine Intelligence, 2007, 29(1): 1-14.

[7] GRIGORESCU C, PETKOV N, WESTENBERG M A. Contour detection based on nonclassical receptive field inhibition[J]. Image Processing, 2003, 12(7): 729-739.

[8] PAPARI G, CAMPISI P, PETKOV N, et al. A biologically motivated multiresolution approach to contour detection[J]. Journal on Advances in Signal Processing, 2007(1), doi: 10.1155/2007/71828.

[9] PAPARI G, CAMPISI P, PETKOV N. Contour detection by multiresolution surround inhibition[C]//IEEE International Conference on Image Processing. Atlanta GA, USA: IEEE, 2006: 749-752.

[10] 闫超, 张建州. 多水平外区抑制的轮廓检测[J]. 中国图象图形学报, 2012, 17(6): 664-670. YAN Chao, ZHANG Jian-zhou. Contour detection based on multilevel inhibition[J]. Journal of Image and Graphics, 2012, 17(6): 664-670.

[11] PAPARI G, PETKOV N. An improved model for surround suppression by steerable filters and multilevel inhibition with application to contour detection[J]. Pattern Recognition, 2010, 44(9): doi:10.1016/j.patcog.2010.08. 013.

[12] PAPARI G, CAMPISI P, PETKOV N. New families of fourier eigenfunctions for steerable filtering[J]. IEEE Transactions on Image Processing, 2012, 21(6): 2931-2943.

[13] CANNY J F. A computational approach to edge detection[J]. Pattern Analysis and Machine Intelligence, 1986, 8(6): 679-698.

[12] XU X M, QIAO Y L. Dynamic textures segmentation based on Markov random field[C]//Second International Conference on Instrumentation, Measurement, Computer, Communication and Control. [S.l.]: IEEE, 2012: 940-943.

编 辑 叶 芳

作者简介：闫超(1985 − )，男，博士生，主要从事计算机视觉方面的研究.

收稿日期：2014 − 08 − 10；修回日期： 2015 − 09 − 25

中图分类号TP391

文献标志码A

doi:10.3969/j.issn.1001-0548.2016.01.023