“讲道理”的课堂：生动与深刻的完美演绎———以罗鸣亮老师的课堂教学为例

郑梅春

一、出其不意，感受课堂灵动之美

数学课堂教学是师生之间交往互动与共同发展的过程，在这个过程中教师需要创设意料之外的惊奇，让学生在常规处质疑，在本质中思考，激发学生主动学习的兴趣，让数学学习变得更为生动有趣，让课堂教学充满“出其不意”的惊喜。

例如，罗老师在执教《小数的意义》一课时，从数数入手，让学生明白正方形卡片涂色部分不满“1”时，用小数表示得先把卡片平均分成十份，看取几份就是零点几。紧接着，罗老师又借助信封，和学生玩起了“信封猜小数”的游戏。

师：我们再来猜一猜，如果老师信封里的正方形，涂色的有4块，你们猜是哪个小数？

生：0.4。

师：一定？

生：肯定！

罗老师慢慢从信封抽出了卡片。（如图1所示）

图1　

图2

生：老师，你错了。

师：老师哪错了？

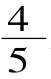
师：那还能用小数表示吗？生1：不能。

生2：可以的，只要把这5份中的每一份再平均分成2份，变成10份，那么涂色部分就成了8份，是0.8。（如图2所示）

师：还想继续猜小数吗？要什么提示？

生：要提示平均分成10份，并且知道取了几份。

师：好！就按照你们想的来，确定平均分成10份，但涂色要比8份多。

生：0.9。生：1.0。

师：还有吗？生：没有了。

老师故意慢慢地把信封里的卡片抽出来。学生看到露出图3顶端部分，都大声高呼到“0.9”。

师：为什么是0.9？

生：因为把卡片平均分成了10份，涂了其中的9份，所以是0.9。

师：一定吗？

生：一定！

老师把卡片完整地抽出来，学生一片哗然。随后，便是一阵热烈的回应。

图3　

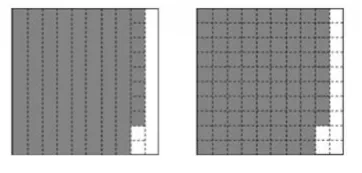
图4

生：老师，你又骗人，不是0.9！

师：不是0.9，那该用哪个小数表示呢？

生1：要把那个0.1再平均分成10份。

生2：就要把这个正方形平均分成100份。

师：为什么还要再平均分？

生3：因为不够0.1，所以要再平均分成十份，才知道是多少。

生4：老师，我猜有可能是0.87……

在学生们争先恐后的猜测中，罗老师分别再把卡片用课件做了如图4所示的平均分。学生都得到了0.88这个答案，并说出了自己的想法。

在让学生用“信封猜小数”的环节中，教师创设了平均分成5份的这一意外，让学生经历了从不能用小数表示到想出办法用小数表示这一思维变化过程，深刻认识了小数是十进制分数的这一本质。接着在认识两位小数时又出其不意地设置了悬疑，让学生误猜0.9，从而引出两位小数产生的必要性。整个教学过程，学生从肯定猜测到自我否定到最后的寻求办法解决问题，都围绕着小数的本质进行讲道理，课堂充满思维和智慧的撞击，学生的学习兴致盎然。

二、追本溯源，领略思维深刻之美

郑毓信教授认为：“优秀教师的特色不应局限于教学方法或模式，也应体现其对教学内容的深刻理解，反映他对学习和教学活动本质的深入思考。”对数学教师来说，在教学中，不但要向学生展示既定的数学知识，还必须能够解释其中的道理：为什么要认识它？它是怎么产生的？对概念、公式、定理等不能满足于形式上的理解，而要明白其来龙去脉、知识串联，既要重视其内涵，也要把握其外延；对数量之间或形体之间的逻辑关系要建立整体的认识，联通各知识之间的关系，正确把握数学知识之间的因果关系。

例如，罗老师在执教《近似数》一课创设了猜“摩托车价格”的活动：

师：老师买了一辆摩托车的价格大约是8000元，猜猜，摩托车的价格实际是多少？猜对了就可以获得独家赞助的摩托车卡片一张。

生：可能8001。

生：8002。

生：7999。

师：还有吗？这个价格好猜吗？有没有好一点的办法？

（教师出示如下“数轴”，让学生把猜测的摩托车价格标在数轴上）

生：我写的是 8200，在8000前面一点。

生：我写的是 7999，比8000少，在8000的后面一点。

生：我写的是8000左右。

师：左右？什么意思？请到前面来表达你的想法。

（这名学生上去把7000和9000之间都用粉笔涂上了，如下图。

全班同学都笑了，此时，教师不置可否，拿出四张卡片）

师：我把摩托车价格写在牌子上，千位可能是几？

生：7或者 8。

师：如果千位是7，那百位可能是几？

生：百位可能是0～9。

生：百位可能是5～9。

此时，前面那名涂色的学生站起来了，说了如下一段话：

生：百位应该是等于500或大于500的近似数。老师，我要上黑板擦掉一些。

说完就噌噌噌地跑上去，把原来画的图擦掉一部分（如下图）。然后开始讲道理：

生：要大于7500的才能约等于 8000。因为 7499靠近7000,7500后面的数才靠近8000，所以7000～7500这里的数不能要。（学生掌声）

生：老师，我还要把8500后面的擦掉（又跑上去擦掉）。因为8500后面的数更靠近9000，那就变成约等于9000了。

师：对了，数学是讲道理的，这就是为什么要“四舍五入”的道理。

学生这一自悟说理的过程，我们看到了学生原先对近似数区间的感知是不清晰的，他们知道用“四舍五入”的方法来求近似数，而对为什么要“四舍五入”却是懵懂的。罗老师根据学生的认知特点，借助数轴的直观，学生通过辨析、讨论，加深了对近似数的认知。学生在讲理过程中，逐步明晰近似数是与实际接近的数，规定“四舍五入”是因为其与实际的准确数更为接近，让学生对于近似数能表示一个区间有了更丰富、更清晰的认识。我们可以看到，学生的思维在追溯“为什么四舍五入”的过程中逐步走向深刻。

三、推理探究，感悟数学理性之美

著名教育家苏霍姆林斯基说：“在我们每个人的内心深处，都有一个根深蒂固的愿望，那就是希望自己是一个发现者、探究者，而在儿童的内心深处，这种愿望尤其强烈。”在教学中，要充分调动学生内心深处的探究欲望，在分析验证中去感受数学推理所带来的成功喜悦。

罗老师《探究 2、3、5倍数特征的道理》一课，让我们深刻领略到，学生在推理探究过程中从内心所焕发出来的对数学学科的喜爱。

问题：为什么判断一个数是不是5的倍数只要看个位数，其他数位都不用看？

师：先独立思考，再同桌交流。

生：双数个5相加个位是0，单数个5相加个位是5，自然数能分成两类，一类是单数，一类是双数，所以答案末尾必须是0或 5。

生：我和我的同桌有一种想法，就是一个奇数乘以5，它的个位一定是5；一个偶数乘以5，它的个位一定是0。

生：我有补充，如果去掉个位的话，末尾就是0，末尾为0的一定是5的倍数，所以只要看个位是不是5的倍数就行了。

师：谁听懂了他的想法？

生：他的意思是，不管多大的一个数，去掉个位余下的数一定是整十数，再加个位上的5或者是0，这样的一个数肯定是5的倍数。

师：（在计数器的十位上拨1）是不是5的倍数？（是）为什么？

生：因为它表示1个十，一个十是5的倍数。

师：（将计数器藏在桌底下）我在十位上拨，还是不是5的倍数？（是）你们没看到，怎么还能肯定？

生：因为每个十都是由2个5组成的，无论十位上拨几个十都是5的倍数。

师：我在百位上拨，还是5的倍数吗？（是）为什么？

生：100里面有10个十，十是可以被5整除的，10个十除以5等于20，百位表示的是有几个百，不管几个百都是5的倍数。

师：猜猜接下来我会在哪一位上拨？

生：千位。

师：对不起，你们都猜错了。我为什么不在千位上拨了？

生：因为千位跟百位、十位都一样。1000是由10个一百组成，而一百是5的倍数，所以千位不管是几都是5的倍数。

师：（将计数器藏在桌底下）我在个位上拨，还是5的倍数吗？

生：不确定。

师：现在为什么不确定？

生：假如你拨了1个，就不是5的倍数；在个位拨5才是5的倍数。

生：现在我明白了为什么判断是不是5的倍数只看个位，其他数位不用看的道理了。

师：5的道理是这样，想想5的道理和哪个数是一样的？

生：和2是一样的，个位上是 0，2，4，6，8 的数，都是 2 的倍数。

师：为什么只看个位呢？

生：10是5个 2，100是 50个2，1000是500个2。个位上只有 2，4，6，8 是 2 的倍数，3 和5都不是2的倍数。

师：那3的倍数，为什么要看各位上数的和？

生：因为3的倍数的个位是不确定的，可能是0，可能是1，可能是2……所以不能只看个位，得总体来看。

师：为什么个位不确定？为什么要总体来看呢？

生：因为10不能被3整除，还有余数，所以每个数位都要看。

师：那为什么判断3的倍数又要把各个数位上的数加起来呢？你们能试着研究吗？

……

推理可以分成合情推理与演绎推理，其中合情推理包括归纳推理与类比推理，本节课，罗老师让学生自主探究，把推理方法应用得淋漓尽致。5的倍数为什么只看个位，学生从举例入手，从十位不用看类推到百位、千位等都不用看的道理，从而归纳出5的倍数只看个位的道理。而从5的道理又类比迁移推理到2为什么也只看个位，3却要看各个数位。整个过程，学生不断地调动思维进行讲理，在比较、判断中，逐步推理出判断数的倍数特征背后潜在的道理。在判断3的倍数为什么要计算各个数位之和，更是把演绎推理和合情推理有效结合，让学生真正喜爱上了探究，以至于在课的最后，学生发出如此的感慨：“我觉得平时我们上数学课老师直接教我们方法，这节课我们是寻找为什么要这样做。刨根问底，总结方法。”“这一节课不知道有没有改变其他人，但至少改变了我，颠覆了我对数学的理解。学习数学不是简单地记住公式就可以了。”学生在这节课上，充分感受到了数学理性的魅力。

郑毓信教授提出：数学教育主要应当促使学生更为积极地去进行思考，并能通过数学学习学会思维，特别是能逐步学会想得更深、更合理、更清晰、更全面。从罗老师的课堂我们看到了：让学生在寻求数学本质的过程中明晰数学道理，真正让数学课走向“深刻”和“生动”，这样的“讲道理”课堂，正是我们学生所喜爱的、教师所追求的精彩课堂！