《认识面积》教学的重构与思考

龚斌斌

【教学内容】

什么是面积呢？2011版新教材中取消了原来“物体的表面或封闭图形的大小就是它们的面积”的定义，取而代之的是“某件物品表面的大小就是某件物品表面的面积”这样的描述，这里的“大小”不是有的大、有的小“相差”的意思，而是“每个面各有确定的大小”的意思。面的大小可以通过测量得到，测量是将一个待测的量和一个公认的标准量进行比较的过程，这个标准量就是“面积单位”。基于这样的思考，笔者对教材中提供的学习材料进行了整合与优化，在核心概念的深度、广度和贯通度上做文章，让学生真正把“面积”学懂、学活、学透。

一、导学材料结构化——从“面”到全面

结构化材料就是从数学知识结构和学生的数学认知结构出发设计和组织的学习材料，以完善和发展学生原有数学认知结构为目的。即教师要从数学知识体系高度“结构化”的特点和学生认知结构的形成、发展规律出发，站在整体、系统和结构的高度把握学习材料，提高学生原有认知结构的可利用性、稳定性与清晰性，为新知识融入已有的认知结构创造条件。

【案例描述】

师：能用“面”字组词吗？

生：面包、面条、表面、上面、桌面……

教师根据学生的组词，分类介绍“面”在字典里的几种意思，提示“表面”的含义。

师：你觉得表面是什么样的？

生：平的、各种形状的，不是内部的、光滑的、弯曲的……

师：能举个例子和大家说明吗？

生：黑板面是平的；练习本的表面是长方形的，我这块橡皮的表面是小鸭形的；文具盒的表面就是文具盒外面这里，不是放铅笔的里面；玻璃窗表面是光滑的，墙面就点粗糙了；球的表面是这样弯曲着的……

师：马上在身边找两样物体摸一摸它的表面，说说表面在哪里，是怎样的？

师：谁愿意介绍数学书的表面？

生：这一圈都是数学书的表面。

生：我知道上面这个面叫封面，下面这个面叫封底，还有左面这个面……

生：我还知道数学书上、下、左、右、前、后一共有6个面。

生：它们都是长方形的。

师：同学们不只找到了数学书的表面，还发现了它不同方向上的表面。这里的四个面，我们也可以叫它的侧面。（教师边摸各方向的面边说）

课始导学的学习材料就一个“面”字，却唤起了学生对“面”“表面”的原有认知结构中的知识点，如平面、曲面、各种形状的面。在描述各种面的样子时，又生成很多新的学习材料，这些新材料成为学生明晰表面概念的一个个“生长点”，表面的数学含义逐步纳入到学生的认知结构中。最值得一提的，从数学书的表面介绍中，理清了学生原有认知中的几个误区：一是简单地认为表面就是外面；二是对表面的单一性认识，认为向上的面才是表面。一个“面”字、一本数学书，两个简单的学习素材恰到好处地把握了学生思维的发展点，全面地认识了“面”。

二、研学材料数学化——从“比“到对比

《数学课程标准》中指出：数学教学是数学活动的教学。这个过程中要引导学生用一种新的思维方式进行一种思维活动，而不是简单的程序操作。这就需要教师提供有效的学习材料，利于学生通过观察、比较、类比、归纳找出事物的共性和规律，形成数学的抽象和概括，对数学有本质的领悟，逐步形成数学化观念。

1.比出大小。

【案例描述】

师：数学书的封面和它的这个侧面哪个大？

生：封面大。

师：像这样说（数学书的封）面比（数学书的侧）面大。

师：说说理由？

生：封面是这么一大块长方形，侧面只是这么一小条长方形，所以……

师：一眼就看出来了是吗？

生：封面和侧面的两个长方形都是一样的长，封面宽一些，侧面细一些，所以……

生：用我的封面和同桌的侧面比一比，就知道了（边说边比）。

师：大家想到了观察、重叠这些不同的方法来比出数学书封面和侧面的大小。数学上“物体表面的大小，就是物体表面的面积”（板书）。数学化地比它们的大小怎么说？

生：（数学书封面）的面积比（数学书侧面）的面积大。

师：选面前的两样物体，比比它们表面的面积，像这样说一说。

教师在此环节中仍然采用数学书作为学习材料，在比较封面和侧面的大小时，不只让学生说出比的结果，还追问“说说理由”，让学生经历数学化的过程，体会可以通过观察、重叠或测量等比出大小。

2.比出异同。

【案例描述】

师：生活中的物体表面都有面积，那我们学过的平面图形有面积吗？

课件呈现：

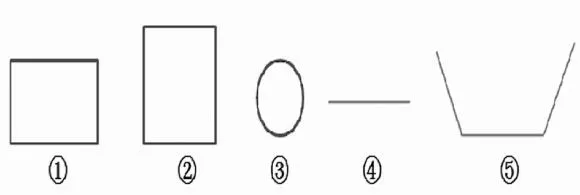
生：④号和⑤号图形没有面积。

师：为什么没有面积？

生：④号是一条线段，它只有长度；⑤号图形没有围起来，所以没有面积。

师：他对④号线段的解释怎么样？好！我们把它请出去（隐去④号）。

师：他说⑤号图形没围起来就没有面积是什么意思？

生：没围起来就没有面，⑤号也只有三条边的长度。

师：你们听懂了吗？用电脑画图时，给⑤号图形涂颜色会发生什么情况？

生：整个屏幕都被涂上了。

师：是呀，所以只有封闭图形才有面积（板书），我们把⑤号也请出去（隐去⑤号）那①号、②号、③号图形都有面积吗？它们还有什么？

生：还有长度。

生：是周长。

师：这些封闭图形既有面积，又有周长？怎么在图上表示出来？

生：（屏幕前比划）涂满色的这块大小就是这个图形的面积（电脑及时演示涂色）；这外面一圈的线的长度就是这个图形的周长（电脑及时演示描线）。

师：它们三个图形谁的面积大？

生：圆的最小。

一份辨析式的学习材料，既揭示了封闭图形也有面积，也在学生的辩论分析中发现不封闭的图形只能量出长度，而封闭图形有周长也有面积。同时，通过学生现场涂、画，体会周长与面积的不同，也隐含着周长是长度可量，面积也可量。

3.比出矛盾。

【案例描述】

师：周长能用尺子量出来大小，面积怎么量？比如说我们的课桌面，它的面积多大？

生：也用尺量。

师：怎么量？

生：……

师：说不清楚是吗？能不能选一个工具来量，比如说数学书？

生：能！看看桌面能摆几本数学书。

师：那别的工具也行吗？（生:能）下面各小组成员合作，选择一样工具来量课桌面的面积，说说课桌面大约是（）个（）面。

（学生活动后组织汇报：12个信封面、10本练习本、5本数学书、6个信封面……）

师：你们量的都是教室的课桌面？你们的课桌都一样大？这是怎么回事？（指着板书上的汇报情况）

生：我们用的工具不一样。

师：那这两组同学都用的是信封，怎么也不一样？（两个小组的同学连忙举起各自的信封）原来两个信封工具也不一样，那对这次测量你们有什么想说的？

生：随便找工具不行，得用一样的工具。

师：就是得有一个标准才行，是吗？

面积可量对学生来说不难理解，只是怎么量没有方法。本次活动的学习材料仍然是就近取材，一个是课桌，一个是装学具的信封，还有就是学生自己的学习用品。面对老师提出的用自选的工具量一量的办法，学生最初没有过多的思考，但是数据汇报出来的同时，引发了学生的认知冲突。在认知矛盾中学生明确地提出要用一样的工具，也就是统一测量的标准才行。这样的安排比教材中小精灵提出的“可以用一种图形作单位来量”要求更具体，让学生自己经历了数学建构、解构、重构的过程。

4.比出优劣。

【案例描述】

师：信封里为各组准备了一样的标准图形，请你们量出剩下这两个图形的面积。

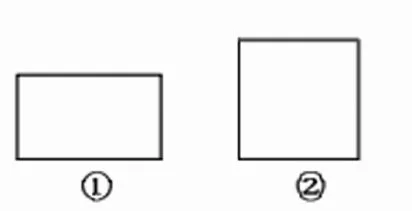
生：我们是用小正方形量的，长方形是8个小正方形，正方形是9个小正方形；

生：我们是用圆形量的，长方形摆了8个圆形，正方形摆了9个圆形；

生：我们是用三角形量的……

师：现在全班出现了三种标准，我们把它们都请上来，（屏幕投影）大家讨论讨论，哪个标准作面积的“尺子”最合适呢？

生：正方形的能铺满，另外两种图形都有空余，那就不是它的面积了。圆形摆起来不方便，三角形还能两个拼着摆……

教师仍选用教材提供的三种图形素材，但为每组只提供了一种图形，全班进行对比分析，各组在应用材料时就发现了自己的图形标准的优劣，明确了选择图形标准时，既要铺满要量的表面，还要拼摆方便的道理。

三、固学材料层次化——从“思”到反思

每节课上的巩固练习是让学生从“会”过渡到“熟”;再由“熟”过渡到“活”的一个过程。好的练习材料，能引起学生思考的同时促进学生的反思学习，往往会收到事半功倍的效果。

材料一：

图片材料（由课件依次展示）：

问题材料：（1）这个图形有面积吗？面积是多大？（2）提供方格图后，能表示它的面积了吗？（3）变个魔术，黑色图形的面积是16个方格，面积变大了吗？

材料二：

画一画：画一个与下图面积一样的图形，想一想：他们的面积为什么相同？

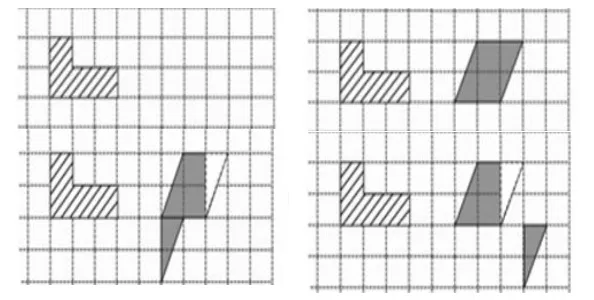
面积作为量与计量范畴的教学内容，在本课教学中有三方面的问题：一是量什么？度量的对象可以是桌面、书面、黑板面、地面等；二是用什么量？学生对面积单位的选择经历了从非标准单位到标准单位的过程；三是怎么量？面积单位要铺满所度量的对象。三个问题呈螺旋形递进，学生的思维也要螺旋上升，才能对面积的“面”和“大小”有深入的认知。由上述两份学习材料可以看出，一幅L形图贯穿了全部的练习，可以说是一材多用，小“材”大用。通过材料一的练习，学生经历了“量什么？用什么量？怎么量？”的思考过程，问题（3）又将学生的思考推向质疑，推向反思，反思中面积的概念得以重构。材料二中有一个重要的画等积图形的活动，该活动又将“量”的知识深化，学生又要经历“画什么？用什么画？怎么画”的思考过程，思考时又要不断倒退一步，反思自己的操作，反思前面的思考，形状变了、摆放形式变了……可面积不变，面积守恒的思想无需定义就已经深入学生的头脑中了。

“材料引起学习，材料引起活动”。不同材料的选择与使用、材料的不同组织与呈现，往往会影响学生的数学经历和感悟，甚至影响学生对数学知识的理解和数学能力的形成。因此，我们每一位教师要不断提高自己的数学素养，提高自己对学习材料的理解和把握能力，课前精心设计教学和选择学习材料，思考和挖掘每一个学习材料的教育价值，课中把握材料生成，使学习材料的作用得到充分发挥。只要我们牵好学习材料之手，整体把握，精心梳理，智慧引领，定能让小“材”大用!