STFT与WVD在地震波时频分析中的应用
2016-04-01刘希康丁志峰李媛崔仁胜1中国天津300180中国地震局第一监测中心2中国北京100081中国地震局地球物理研究所3中国北京100036中国地震局地震预测研究所
刘希康丁志峰李 媛崔仁胜1)中国天津300180中国地震局第一监测中心2)中国北京100081中国地震局地球物理研究所3)中国北京100036中国地震局地震预测研究所
STFT与WVD在地震波时频分析中的应用
刘希康1), 2)丁志峰2)李 媛1)崔仁胜3)
1)中国天津300180中国地震局第一监测中心2)中国北京100081中国地震局地球物理研究所3)中国北京100036中国地震局地震预测研究所
摘要地震波是一种非平稳信号,传统的傅里叶变换已不适用,时频分析方法能在时间—频率域给出非平稳信号不同时刻的频率分布特征。Wigner-Ville分布(WVD)对非平稳信号具有较好的时频聚集性,但因其为双线性变换,会产生严重的交叉干扰项。短时傅里叶变换(STFT)是一种线性变换,不存在交叉项干扰,但时频聚集性较差。考虑到二者优点,在对地震波进行时频分析时,采用短时傅里叶变换和Wigner-Ville分布的联合算法,既有效抑制了Wigner-Ville分布交叉项干扰,又保持了较高的时频聚集性。通过3种方法,对模拟信号和实际数据处理结果进行对比分析,发现联合算法对获取地震波信号的时频特征和纵波到时检测,具有更好效果。
关键词短时傅里叶变换;Wigner-Ville分布;时频分析;地震波谱
E-mail:xikangliu@126.com,电话:15501065900
本文收到日期:2015-11-02
0 引言
根据信号的统计特征,将信号分为平稳信号和非平稳信,各统计量(如频率、相关函数、功率谱等)随时间变化的信号为非平稳信号(张帆等,2006)。传统的傅里叶变换,对信号的表征要么完全是时间域,要么完全是频率域,不能分析信号中频率随时间的变化关系。因此,傅里叶变换无法表述信号的时间—频率局域性质,而此性质恰是非平稳信号的根本性质。
时频分析或称时频分布,是描述信号频率随时间变化的方法,采用时间—频率联合表示信号,将一维时域信号映射到二维时频平面,在时频域内对信号进行分析,全面观测信号的时间—频率联合特征,同时掌握信号的时域及频域信息(赵淑红,2010;刘希康等,2013)。
短时傅里叶变换(short-time Fourier transform,STFT)是一种线性变换,对多分量的非平稳信号不会产生交叉干扰项,但由于采用固定窗,使得时间和频率分辨率难以同时达到最优,时频分辨率较差。Wigner-Ville分布(Wigner-Ville distribution,WVD)具有理论上的最高时频分辨率和许多优良的数学性质(王见等,2013),但因其为双线性变换,对多分量的非平稳信号存在严重交叉项干扰。因此,可以通过某种算法,将STFT 与WVD关联起来,即STFT与WVD的联合算法,在不失去WVD良好时频聚集性的情况下,消除交叉项干扰,得到同时具有较好时频聚集性且无交叉项的地震波谱图,提高地震波时频分析的可读性。目前,二者联合表示方法主要是,利用短时傅里叶变换线性变换无交叉项的特性,抑制Wigner-Ville分布交叉项干扰。吕宙等(2009)主要应用于航天电子对抗雷达线性调频信号检测研究;赵淑红(2010)利用二者直接相乘方法,提取模拟线性调频地震波信号的瞬时频率;王见等(2013)利用二者联合方法进行机械转轮故障检测研究。本文利用二者联合表示方法,用于地震波时频分析和纵波到时检测。
1 算法原理
1.1 WVD的定义
假设实际信号x(t)的解析信号为s(t),其WVD定义为
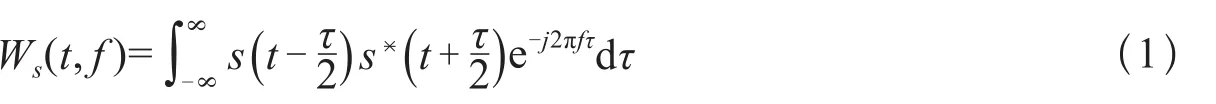
WVD是一种双线性变换,不满足叠加原理。对于2个分量的信号:x(t) = x1(t)+x2(t),其WVD结果为

其中,信号自项为Wx1、Wx2,而交叉干扰项为Wx1x2。WVD的交叉干扰项是无法避免的,严重影响区分信号项和交叉项,多分量信号交叉项干扰更为复杂、严重。
图1(a)所示为包含4个高斯元信号的时域信号,采样率为1 Hz,振幅均为1。在32 s处,两个高斯元信号频率中心分别为0.15 Hz和0.35 Hz,持续时间20 s;在96 s处,两个高斯元信号频率中心分别为0.15 Hz和0.35 Hz,持续时间也为20 s。图1(b)为该信号的WVD分布,可以看出其具有明显的交叉干扰项,无法分辨原信号分量和交叉干扰项。
因而,为了减小交叉项干扰,对设计不同核函数提出很多方法,例如:伪Wigner-Ville分布(PWVD)、平滑Wigner-Ville分布(SWVD)、Born-Jordan分布、Choi-Williams分布(CWD),等等(赵淑红,2010;刘希康等,2013),统称为Cohen类时频分布。

1.2 STFT及其谱
信号x(t)的STFT定义为

由于信号x(t)乘以一个短窗函数w(t)等价于在分析时间点t附近的取一个切片,所以短时傅里叶变换可以理解为信号x(t)在时间点t附近的傅里叶变换,即“局部频谱”(胡昌华等,2002;吕宙等2009)。
由定义可知,短时傅里叶变换是一种线性变换,对多分量信号来说,不存在交叉项。由不确定原理可知,短时傅里叶变换(短时傅里叶变换英文缩写STFT,为了描述连贯采用中文全称)的时间分辨率和频率分辨率不可能同时变小,其时宽—带宽乘积存在一个下限,短时傅里叶变换的时频聚集性由此受到限制。由于高斯窗函数达到时宽—带宽积的下界(科恩,2000),因此本文进行短时傅里叶变换使用高斯窗函数。
WVD是一种二次型变换,为了与WVD对比,一般使用短时傅里叶变换谱。短时傅里叶变换谱的定义为STFT模的平方

图1(c)为上述高斯元信号的短时傅里叶变换谱。与图1(b)相比,短时傅里叶变换谱无交叉干扰项,但时间频率分布范围较宽,时频聚集性比WVD差得多。
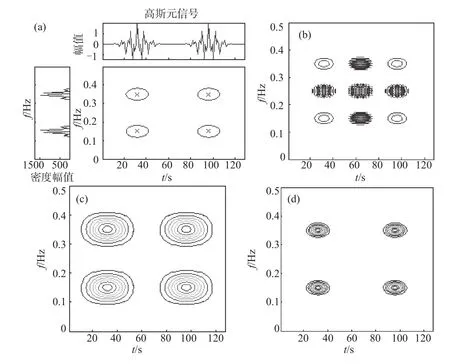
图1 四分量高斯元信号、能量谱密度及其时频分布(a)高斯元信号能量谱密度及其理论时频;(b)信号(a)的WVD分布;(c)信号(a)的STFT谱分布;(d)信号(a)的STFT谱和Wigner-Ville联合方法分布Fig.1 Signal of 4 Gauss atoms, energy density and the time-frequency diagrams
1.3 STFT与WVD的联合算法
从STFT和WVD各自优缺点出发,可以得出,由于STFT是线性变换,不存在交叉干扰项,能够正确反映信号的各分量信息,但时频聚集性不好,分辨率较低;对于WVD,具有很好的时频聚集性及较高时频分辨率,但存在严重交叉干扰项。因此,可以对二者进行联合计算,结合二者优点,可得到既不含交叉干扰项而时频分辨率又高的分布。
当得到信号的STFT谱和WVD后,二者联合算法可定义(王见等,2013)为


式(6)为取STFT谱和WVD中数值较小者,按此处理,将WVD中有交叉项部分用相应STFT谱中的数值代替,以达到消除交叉项的目的。式(7)中c为STFT谱的交叉项消除阈值。当STFT谱的值小于该阈值时,返回0;如果大于该阈值,则返回1。WVD中有交叉项对应STFT谱部分的数值肯定小于该阈值,用数字0与WVD相乘以消除交叉项。式(8)中“·”代表矩阵的点乘,α、β称为幂调节系数。该式的作用是增强两变换数值较大部分而消弱有交叉项部分。一般随着α、β的增大,STFT和WVD联合变换的时频聚集性会提高,在实际应用中,需灵活调试α、β取值,以免丢失某些有用信息。式(8)较式(6)、式(7)结果更加理想,使用更为灵活。
图1(d)为STFT谱和WVD联合算法对图1(a)信号的处理结果,可以看出,该方法既克服短时傅里叶变换固定时频分辨率的缺陷,又在消除WVD交叉项干扰的同时保留了良好的时频聚集性,与信号的理论频率保持一致,具有较高的时间—频率分辨率。
2 资料处理结果
2.1 地震波谱时频分析
以2013年9月4日莆田ML4.8地震为例,选取福州日溪地震台(FZRX)南北向分量记录进行地震波谱时频分析。台站距震中约102 km,采用CMG-3ESP型宽频带地震仪,采样频率100 Hz。
由于联合算法对计算机内存需求较高,为降低计算量,截取2013年9月4日06时23 分39秒至2013年9月4日06时24分29秒,时长为50 s的地震波形进行时频分析(假设截取波形开始时刻为0秒)[图2(a)],能量谱密度见图2(b),可以发现,其能量主要集中在小于5 Hz的频率范围内,少部分在5—10 Hz,说明该记录为低于5 Hz频率成分为主的地震波。图2(c)为莆田ML4.8地震波形的Wigner-Ville分布,能够较好反映该地震波的时频分布特征,频率和能量谱密度分布一致,15 s前后横波到达,能量达到最强,由于纵波能量相对较弱,时频域内纵波未达到最大幅值的5%以上,图中没有很好地显示出来。另外,由于地震波的非平稳特性,受噪声和自项相互干扰等影响,不难发现,时频图像存在较多干扰成分,与有用信息混合在一起。

图2 福州日溪地震台(FZRX)南北向记录及其能量谱密度和Wigner-Ville分布(a)南北向记录波形;(b)能量谱密度;(c)Wigner-Ville分布Fig.2 Energy density and Wigner-Ville distribution of FZRX Seismic Station NS component waveform record
2.2 纵波到时检测
为清楚验证STFT和WVD联合方法对提取地震波波谱时频特征和纵波到时检测的有效性,截取上述地震台站记录2013年9月4日06时23分39秒至2013年9月4日06时23分54秒,包含P波前后共15 s的三分量波形进行分析(假设波形开始时刻为0秒),图3(a)从左向右依次为N、E、U三方向,虚竖线表示P波初动时刻,在该时段内,初动时间读取为3.85 s。

图3 P波三分量记录波形及其不同时频分布(a)三分量P波记录波形;(b)STFT谱和Wigner-Ville联合方法时频分布;(c)Wigner-Ville分布;(d)STFT谱Fig.3 Three component of P waveform and various time-frequency distribution diagrams
图3(b)为利用二者联合算法,由式(8)所得结果,幂调节系数取α = 1.5,β = 1,可以发现,联合算法的时频聚集性较好,同时消除了交叉项干扰,地震记录频率范围主要集中在1—5 Hz,少量分布在5—10 Hz,在P波初动时刻前后能量较强,且P波频率成分和分布形态在三方向上具有较好的一致性,具有从低频向高频变化的明显趋势。
图3(c)为三方向的STFT谱,选取高斯窗函数长度为129,结果显示,因没有交叉项干扰,STFT谱具有较清晰的时频分布图,但是其时频聚集性明显较差,各时刻频率分布散乱,分辨率较差,不能有效判读P波初动时刻,频率成分主要在0—10 Hz。
图3(d)为三方向的Wigner-Ville分布,可以看出,其能量主要集中在5 Hz以下,并且有从低频向高频变化的趋势,能够判读P波初动时间,且与该时段内波形记录文件读取到的P波到时一致,为3.85 s,这也为精确检测P波初动时刻提供了一种方法,但整体看由于噪声干扰和交叉项干扰,有效信号被淹没,存在虚假高频信息,时频分辨率并不理想。
通过以上结果对比可以发现,STFT和WVD联合算法既保留了STFT的线性变换没有交叉干扰项的特性,又保留了WVD的时频高分辨特性,具有较好的时频分布特性,且可以通过灵活调整幂调节系数,根据实际需要得到待分析波形的不同时频分布形态。根据波形读取的P波初动和利用联合方法得到的P波初动时刻一致,说明该方法对P波初动精确检测具有良好效果。
3 结论
本文通过对模拟信号和实际地震记录处理分析,对比STFT谱、Wigner-Ville分布及联合方法的处理结果,得出以下结论。
(1)实际应用发现,短时傅里叶变换受窗口大小影响,时窗太大会导致时间分辨率降低,时窗太小,频率分辨率较低(赵淑红,2010),时间分辨率和频率分辨率不能同时达到最优,窗口大小及类型的选取需结合实际资料,考虑处理目的和要求。
(2)Wigner-Ville分布不包含任何窗函数,可以达到最高的时频分辨率,但存在严重的交叉干扰项,交叉项干扰程度与资料自身所包含的频率成分有关,对实际资料来说,由于频率成分复杂,自项、噪声、干扰项相互叠加,时频分辨率更差。
(3)利用STFT谱和Wigner-Ville分布联合表示方法,对模拟信号和实际数据进行处理可知,此方法结合STFT和WVD的优点,既抑制了WVD交叉项干扰,又保留了时频高分辨率特性,能够精确表示地震波的波谱特征,并检测P波初动时刻。另外,可以根据实际数据处理需要,通过选择合适的窗函数、时窗长度及幂调节系数,在一定程度上灵活显示待分析信号的时频分布特征。
(4)较高、较好分辨率的时频分析方法在爆破识别(沈萍等,1999)、纵波到时检测(邹文等,2006)、工程抗震参数设计(魏来等,2007)等方面均具有重要的研究意义和应用前景。
参考文献
胡昌华,周涛,夏启兵,等. 基于Matlab的系统分析与设计——时频分析[M].西安电子科技大学出版社,2002:2-24.
刘希康. 精密可控震源信号提取新方法研究[D].北京:中国地震局地震预测研究所,2013:4-6.
吕宙. 基于STFT的Wigner-Ville分布交叉项抑制[J]. 航天电子对抗,2009,26(3):27-29.
沈萍,郑治真. 瞬态谱在地震与核爆识别中的应用[J]. 地球物理学报,1999,42(2):233-240.
魏来,刘马群,李奎. 信号分析方法及其在地震波处理中的应用[J]. 洛阳大学学报,2007,22(4):69-73.
王见,李金同,卢华玲,等. 采用STFT-Wigner变换抑制Wigner-Ville分布交叉项[J]. 重庆大学学报,2013,36(8):15-25.
张帆,钟羽云,朱新云,等. 时频分析方法及地震波谱研究中的应用[J]. 地震地磁观测与研究,2006,27(4):17-22.
张鑫,赵拥军. 基于短时傅里叶变换和Wigner-Ville分布的联合变换[J]. 电子对抗,2008,3:39-42.
赵淑红. 短时傅里叶变换与Wigner-Ville分布联合确定地震信号瞬时频率[J]. 西安科技大学学报,2010,30(4):447-450.
邹文,陈爱萍,顾汉明,等. S变换初至拾取技术及其在复杂山区中的应用[J]. 石油天然气学报,2006,28(2):63-65.
[美]科恩著. 白居宪译. 时—频分析:理论与应用[M]. 西安交通大学出版社,2000:35-40.
Application of short -time Fourier transform and Wigner -Ville distribution in time -frequency analysis of seismic wave
Liu Xikang1), 2),Ding Zhifeng2),Li Yuan1)and Cui Rensheng3)
1) First Crust Monitoring and Application Center, China Earthquake Administration, Tianjin 300180,China 2) Institute of Geophysics, China Earthquake Administration, Beijing 100081, China 3) Institute of Earthquake Science, China Earthquake Administration, Beijing 100036, China
Abstract
Seismic signal is a kind of non-stable signal, which can’t be analyzed suitably by classical Fourier analysis. Time-frequency analysis can analyze non-stationary signal in time-frequency domain and show out the distribution characteristics. WVD has perfect time-frequency concentration, but because it is a bilinear transformation, the existence of cross-terms is inevitable. STFT is linear transformation, has no cross-terms, but affected by the window size,it has bad time-frequency concentration. Based on the advantage of these two methods, we propose to obtain the time-frequency distribution by the combined method. This method can suppress the cross-term interference in WVD effectively, while keeping the excellent timefrequency concentration. By calculating simulation signal and actual data, the comparison result of STFT, WVD and the combined method indicates that the combination method is most suitable for computing the time-frequency distribution characteristics of earthquake waveform signal and more effective to detect the arrive time of P-waves.
Key words:short-time Fourier transformSTFT),Wigner-Ville distributionWVD),timefrequency analysis,earthquake spectrum
doi:10. 3969/j. issn. 1003-3246. 2016. 01. 003
基金项目:中国地震局“三结合”(No.163303),科技部公益性行业科研专项“中国地震科学台阵探测——南北地震带北段”(No.201308011),中国地震局第一监测中心主任基金项目(FMC2015005)
作者简介:刘希康(1988—),男,助理工程师,在读博士研究生,主要从事地震观测技术等研究工作。
