MATLAB在洪水过程同频率放大计算中的应用

2016-04-01陆泳舟

东北水利水电 2016年9期

关键词：洪量过程线洪峰

陆泳舟

（上海勘测设计研究院有限公司，上海200434）

MATLAB在洪水过程同频率放大计算中的应用

陆泳舟

（上海勘测设计研究院有限公司，上海200434）

在设计洪水过程线计算中，同频率放大法是最常用的方法之一，但该法在计算中因为各时段流量放大倍比不一致，放大后需要多次人工修整，耗时较多且易造成过程线过度变形。为了使计算结果更客观，过程更高效，可以利用MATLAB软件的计算工具，通过程序优化计算，得到与典型洪水过程形态差异最小的设计洪水过程。本文以南亚地区某大型水库设计洪水为例，阐述MATLAB程序最优化算法工具在设计洪水过程同频率放大计算中的应用方法。

洪水过程；同频率；MATLAB；最优化；水利信息化

1 问题的提出

在水利规划设计中，由设计洪峰、设计洪量推求设计洪水过程线是最常见的计算工作。对于小流域，一般根据设计暴雨过程及地貌单位线计算出设计洪水过程；而对于大流域，则要根据设计洪峰和设计洪量，并选取邻近站点的一场实测洪水过程（即典型洪水），对其进行缩放。洪水过程缩放一般分为同倍比缩放和同频率缩放两种计算方法，前者主要用于峰量关系好及多峰形的河流，计算也相对简单，只要将典型洪水中各时刻的流量乘以“峰比”或“量比”即可；后者常用于峰量关系一般的河流，尤其是调洪作用大的水库，由于峰比和量比不相等，计算量也相对较大，会出现两大问题：

1）放大后的设计洪水过程线与典型洪水过程线往往有较大差异，选取典型的意义被弱化。

2）洪量由多时段控制，计算后，时段间节点处容易出现不连续的情况，需要人为修匀，人为主观性强且耗时多。

因此，针对同频率放大法，需要寻求一种更高效的计算方法，使得结果尽可能保持典型洪水的形状，且减小人为因素的影响。

2 MATLAB的计算优势

MATLAB是美国Mathworks公司开发的一款商业数学软件，可以用于矩阵计算、统计与优化分析、绘制函数和数据、实现算法等，在工程计算、控制设计等领域广为使用，可在Win XP，Win7，Unix等多种系统环境下运行。较之常用的VB、C++程序语言，MATLAB程序有如下优势：

1）对界面的要求低，用户不需要像VB程序设计那样编辑窗体、输入、输出文件链接指令，只需要在命令窗口输入数学语言即可。

2）丰富的内部函数，程序自带有大量的数学计算公式，比如线性插值、求解微分方程、最优化求解等计算，可直接实现，而VB、C++等程序语言只能识别最基本的四则运算符号，编程势必需要用户添加大量的中间变量，代码繁琐且容易出错。

3）具备强大的绘图功能，其本身带有很多用于绘图的库函数，简单易用，可用简单的语句直接将数学结果进行图像表达；而VB、C++等程序语言需要用户编写绘图代码，工作量较大。

因此，在水文水资源学科领域的计算中，MATLAB出色的计算功能被逐渐重视，在流域汇流参数率定、暴雨公式参数拟合等计算都已经被使用。

3 实例分析

3.1 设计洪水和典型洪水

1）设计洪水

以南亚地区某大流域中一座防洪水库为例，该水库集水面积约2.5万km2，洪水调节作用明显。水库上下游附近各有一个水文站，两站都具有超过40年实测资料，因此根据上下游站的实测资料比拟计算坝址处年设计洪峰和设计洪量。计算得2000年一遇设计标准下，年最大洪峰26 031 m3/s，年最大24 h设计洪量15.014亿m3，年最大3 d设计洪量32.438亿m3。

2）典型洪水

根据本工程设计需要，需计算坝址年最大3 d设计洪水过程线。本次计算选择坝址下游水文站1992年汛期的一场特大洪水作为典型洪水，最大流量14 730 m3/s，位于全过程72 h中的第20 h，最大24 h洪量10亿m3，最大3 d洪量18.71亿m3，洪水过程见图1。

图1 典型洪水过程线图

3.2 同频率缩放计算

根据典型值和设计值计算得，洪峰倍比为1.767，最大24 h、最大3 d洪量放大倍比分别为1.501和2.00，将典型洪水过程放大，得到设计洪水过程线见图2。由图2可见，因为各时段的放大倍比不相同，在时段交界点处洪水过程出现波折起伏，不能保持单峰形状，洪水过程较之典型洪水发生了很大改变。按照传统的水文计算，针对此类情况只能人为修匀洪水过程线，处理之后再计算相应的相应的洪量，若与设计值差距较大，则继续修正。整个计算需反复多次，过程耗时很长，而且计算结果主观性强，会因计算者的不同而产生不同的结果。

图2 典型洪水放大结果图

3.3 MATLAB程序求算

3.3.1 程序语言

MATLAB程序可以直接解决数学中的最优化计算：

目标函数：minf（x）

程序调用格式为 [X，fmin，flag，num]=fmincon（Fobj，x0，A，B，Aeq，Beq，x1，xu），其中Fobj为目标函数，x0为初始值，A，B，Aeq，Beq均为矩阵格式。

3.3.2 工程运用

设计洪水过程的计算可以等价为一种最优化计算的数学模型，各参数表达如下：

1）目标函数。

放大后的设计洪水与典型洪水曲线线型差异达到最小化，即各段斜率差异总和最小，见式2。

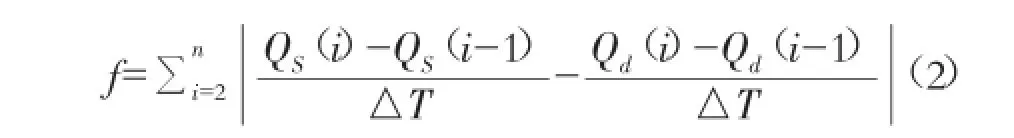
式中：f——目标函数值；n——时刻点总数，14；QS——设计洪水各时刻流量值，m3/s；Qd——典型洪水各时刻流量值，m3/s；△T——时段步长，h。

2）自变量：典型洪水各时刻流量及时段步长。

Qd——典型洪水各时刻流量值，m3/s；△T——时段步长，此次取6。

3）约束条件

洪峰、洪量数值等于设计值；且洪水呈单峰形状；洪峰出现时间与典型洪水一致，即位于第20 h，见式（3）～（7）。

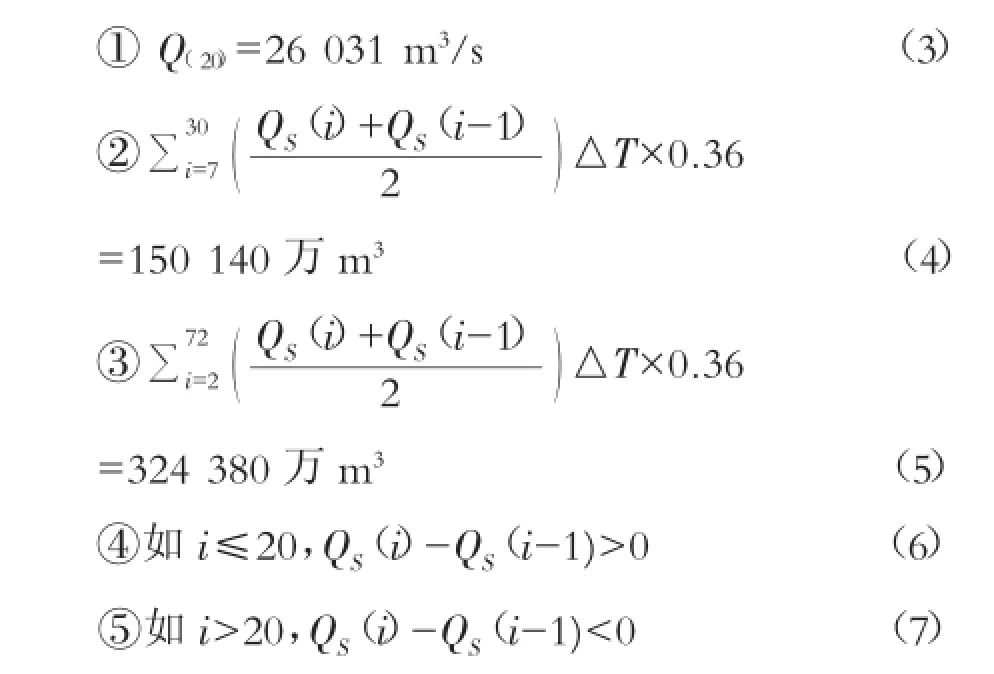
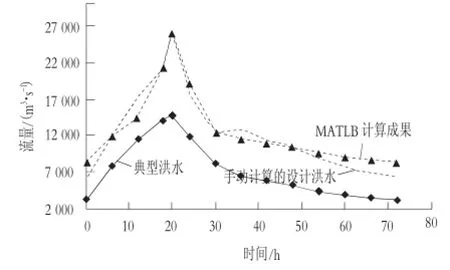
图3 MATLAB计算所得设计洪水过程线

综上所述，洪水同频率缩放的问题已经概化成一个有约束条件的最优化求解数学模型。（3）（4）（5）成等式约束，（6）（7）立形成不等式约束，如3.3.1中所述，经MATLAB最优化工具计算，得各时刻QS值。计算结果如图3所示。与3.2节计算结果相比，MATLAB计算所得设计洪水过程形状更接近于典型洪水，成果优于前者。谨、高效，可广泛用于水利规划设计工作。