基于LCC的配电网开关优化配置研究

郝　培李辰蕊史金刚

（1.石家庄市科技合作与创新平台中心 2.国网青海省电力公司西宁供电公司）



基于LCC的配电网开关优化配置研究

郝培1李辰蕊2史金刚2

（1.石家庄市科技合作与创新平台中心 2.国网青海省电力公司西宁供电公司）

摘要：在市场环境下，电力企业面临更多竞争压力，配电网规划方案全寿命周期经济性变得越来越重要。本文基于全寿命周期成本（Life Cycle Cost，LCC）理论建立了配电网开关优化配置模型，模型考虑了配电网开关优化配置方案的初始投资、全寿命周期运行维护成本及停电损失成本等。该模型兼顾了配电网开关优化配置方案全寿命周期的经济性和可靠性，使得配电网开关优化配置投资和可靠性收益达到最佳平衡，提高了配电网投资的收益能力。利用寻优能率较强的改进遗传算法对配电网开关优化配置模型进行了求解，并用实例证明了本文模型和算法的有效性和实用性。

关键词：配电网；全寿命周期成本；开关优化配置；改进遗传算法

0 引言

用户对供电可靠性的要求越来越高，在配电馈线上配置一定数量的开关设备是提高配电网供电可靠性的有效措施之一。配电网开关优化配置以成本-效益分析原理为基础，通过确定馈线上断路器、隔离开关等开关设备的最佳位置和数量提高系统的供电可靠性。增加配电网中开关设备的数量意味着供电部门需要额外增加投资和维护费用，怎样既能保证供电可靠性，又能获得较好的经济效益，是配电网建设中一个重要的问题。长期以来很多学者对这一问题做了很多研究[1-7]。文献[1]指出了开关优化配置的重点和难点，以及如何提高计算效率。文献[2]提出了关于配电网开关配置的改进遗传算法。文献[3]提出了一种关于配电网开关优化配置的免疫算法。文献[4]提出了一种关于配电网开关优化配置的人工鱼群算法。文献[5]提出了一种将二分法应用于配电网开关优化配置。文献[7]根据动态规划的优化原则，建立了馈线分段开关的配置模型，采用改进的分步最优法求解，实现了配电网开关优化配置。以上方法从不同的角度研究了配电网开关优化配置，取得了不错的效果。但上述方法未考虑规划方案的全寿命周期成本。

配电网具有系统性、长期性的特点，从长远观点看，配电网开关的运行成本、维护成本、停电损失成本有时会大于其建设成本，而且先期建设成本的多少对未来运营成本、维护成本和停电损失成本的多少会产生很大的影响，因此有必要从配电网建设的全寿命周期角度进行配电网开关优化配置。

本论文将全寿命周期成本理论应用到配电网开关优化配置中来。考虑了配电网开关优化配置方案的初始投资、全寿命周期运行维护成本及停电损失成本等，建立了可兼顾配电网开关优化配置方案全寿命周期经济性和可靠性的配电网开关优化配置模型。由于配电网开关优化配置是一个离散的、非线性、多目标组合优化问题。论文结合配电网开关优化配置特点，提出了一种改进遗传算法用于配电网开关优化配置模型求解。用Visual Studio2010开发了配电网开关优化配置程序，实例证明了本文模型和算法的有效性和适用性。

1 基于LCC的配电网开关优化配置模型

本文从全寿命周期成本角度考虑，以配电网开关优化配置方案全寿命周期成本等年值最小为目标函数，建立了配电网开关优化配置数学模型

minLCC=C1+CO+CM+CF（1）

式中，C1为配电网开关设备初始投资成本等年值；CO为配电网年度运行损耗成本；CM指配电网开关设备年度检修维护成本；CF为配电网年度停电损失成本。

各成本的详细计算公式如下：

（1）开关设备初始投资等年值C1

开关设备初始投资包括设备购置成本和建设安装成本，安装建设成本通常取设备购置成本的某一比例，即

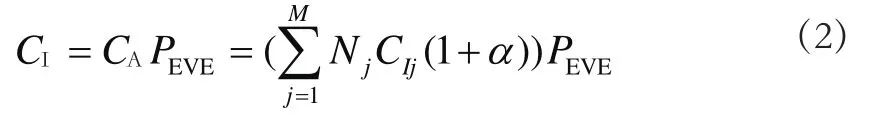
式中，CA为开关设备总投资；PEVE为等年值折算系数，PEVE=r(1+r)n/( (1+r)n-1)，n为设备寿命周期，r为社会折现率；M为开关类型数(如分段开关、联络开关等)；Nj为第j种开关安装台数；CIj为第j种开关价格；α为验建筑工程费和安装工程费系数，根据实际经验本文α 取20％。

（2）配电网年度运行成本CO

年度运行成本主要指配电网年度网损成本。联络开关的安装位置不同，会使系统运行在不同的辐射网状态，系统运行损耗也会不同。如图2所示，联络开关安装在支路23和安装在支路10时，该配网就运行在不同的辐射网状态，其运行损耗是不同的。配电网年度运行成本的计算公式如下

式中，∆P为最大负荷损耗功率，通过配网潮流计算得到；τMAX为年最大损耗小时数；η为趸入电价，元/年。

（3）开关设备年度检修维护成本CM

根据配电网运行实际情况，检修维护成本通常取其配网初始投资的某一百分比，该值需根据实际运行经验确定，本文取初始投资2％，即

（4）年度停电损失成本CF

停电损失是指由于配电系统停电而对用户造成的损失和电力部门售电收益损失。停电损失的计算主要与以下几个因素有关：停电发生的时间、停电持续时间、停电频率和用户负荷性质。用户损失计算采用修正产电比法（通过对各类型质用户的调研数据统计得到），计算公式如下

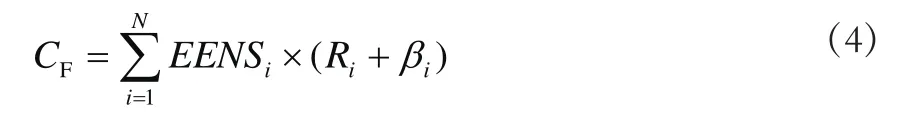
式中，N为该配网负荷点数；EENSi为负荷点i年度电量不足期望值，kWh；Ri为节点i的产电比，元/kWh，不同类型用户的单位停电容量对应的产电比如表1第4列所示；β为供电公司的售电利润，由于供电公司对不同类型负荷执行不同的电价，因此不同类型负荷对应的售电利润也不同，如表1第4列所示。

（5）配网开关优化配置约束条件

式中，Vi为配网节点i的节点电压，Vmin和Vmax为节点电压允许的最大值和最小值；Ij为支路j实际传送电流，Ijmax为支路j最大载流量。

2 适用于开关优化配置的改进遗传算法

遗传算法（Genetic Algorithm，GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，传统GA进行开关优化配置模型求解时，存在求解速度慢、易早熟等问题。若在初始解编码和进化策略过程中，结合配电网开关优化配置的实际情况，引入更多的启发策略能显著减小解的搜索空间，提高算法的寻优能力。

2.1 开关优化配置改进遗传算法启发策略

结合配电网开关优化配置的实际情况，本文提出的启发策略如下：

1）设定合理的开关数量，本文取3～7台；若存在分段开关，则分段开关和联络开关数量比例范围为6:1～2:1；

2）从电源点开始，离电源点越远的支路安装联络开关的概率越大，反之越小，服从正太分布；

3）在寻优过程中若出现环状配电网，需要配置联络开关来解环（联络开关数量小于等于1），解环过程采用策略2）。

2.2 遗传算法的实现过程

1）改进二进制编码

配电网开关配置优化问题实际上就是要进行开关位置和类型的选择。线路中所有可选的位置最终只有三种状态，编码表达式如下

式中，xi=0、xi=1、xi=2分别表示支路i不安装开关、安装分段开关、安装联络开关；n为支路数。

2）开关优化配置求解流程

一个完整的遗传算法应包括以下几个方面：参数选取、编码、遗传操作、适应度评价。配电网开关优化配置的遗传算法求解流程如图1所示。

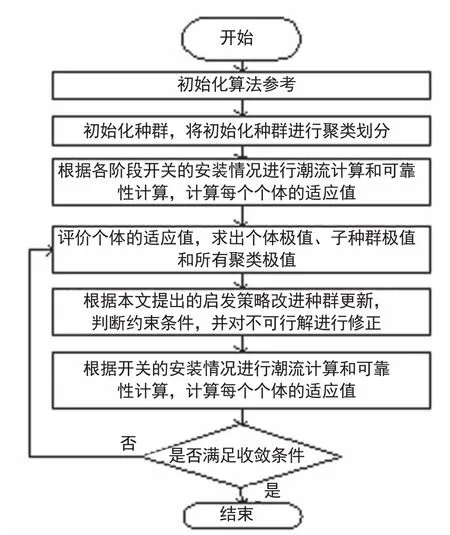
图1　开关优化配置求解流程图

3 算例分析

采用IEEE RBTS-5系统[7]的F1、F2两条主馈线进行开关优化配置，配电网主接线图如图2所示。

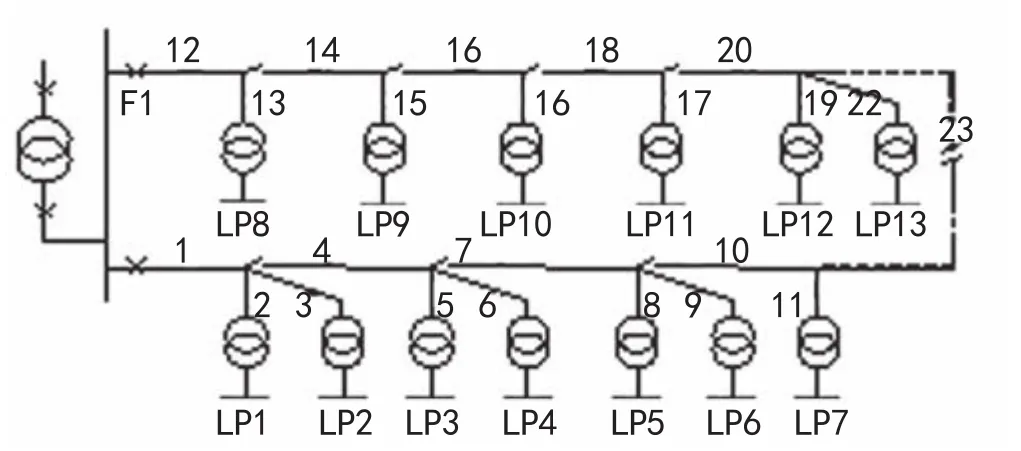
图2　IEEE RBTS-5馈线F1、F2主接线图

图2中各负荷点负荷数据如表1所示，主馈线线路电阻0.299Ω/km，电抗0.096Ω/km，分支馈线线路电阻0.622Ω/km，电抗0.113Ω/km，各支路长度如表2所示。线路的年平均故障率取0.04次/km，平均修复时间取30小时/次，开关倒闸操作时间20分/次，开关投资20000元/台，设备规划使用年限是20年。贴现率取8％，趸入电价取0.45元/kWh。改进遗传算法初始种群数60，交叉和变异操作时的系数分别为0.6和0.02，最大迭代次数100。利用本文建立的基于LCC的配电网开关优化配置模型和改进遗传算对图2所示配电网进行开关配置优化计算，优化结果如表3方案3所示。最优方案的开关配置为：在支路7和支路18安装分段开关，在支路23安装联络开关。

为了体现出本文所提方法的优点，分别与图2所示的配置7个分段开关和1个联络开关方案（LCC成本见表3方案1）和不配置分段和联络开关方案（LCC成本见表3方案2）两种情况进行对比，各方案全寿命周期成本数据如表3所示。

表1　各负荷点用户数据

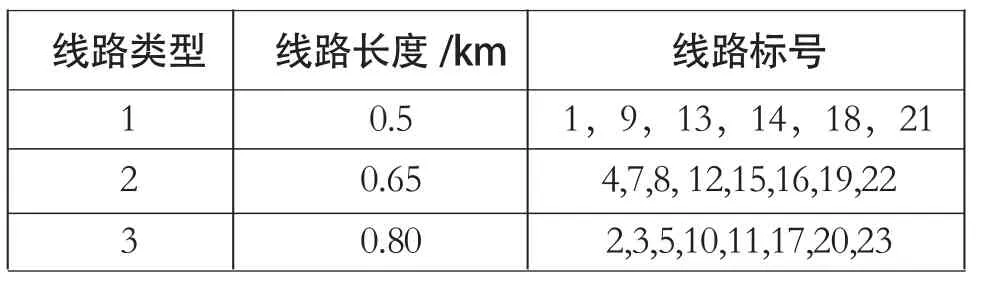
表2　线路类型及长度

表3　不同开关配置方案LCC成本明细表 （单位：元）

由表3数据可以看出，方案3为最优开关配置方案，具有最小的年度LCC成本。另外，由表3还可以看出初始投资低的方案（方案2）不是全寿命周期经济性最优的方案，因为其后期的停电成本较高。而一味追求可靠性的高初始投资的方案也不是全寿命周期经济性最优的方案，因为安装较多的开关设备不仅初始投资大，而且后期的运维费用也高。利用本文方法得到的方案3取得了初始投资、运维成本与停电损失成本的折中，是全寿命周期经济性最优的开关配置方案。

4 结束语

本文基于全寿命周期成本理论，提出了一种以配电网全寿命周期年度综合费用最低为目标的配电网开关优化配置方法，利用改进遗传算法对目标函数进行求解。通过对IEEE RBTS-5配网开关优化配置实例结果分析，得出如下结论：

1）基于LCC理论建立的配电网开关优化配置模型有效折中了初始投资成本、运行维护成本与停电损失成本，有效平衡了配网开关设备投资与配网可靠性的关系，具有更好的经济性。

2）由规划方案LCC结果可以看出，配电工程运营阶段成本（维护成本、运行成本、停电成本）占很大比重，基于LCC方法的规划结果更科学、合理，具有较高的实用价值。

参考文献：

[1] 谢开贵,刘柏私,赵渊,等.配电网开关优化配置的动态规划算法[J].中国电机工程学报, 2005(6): 25-17.

[2] 王峻峰,谢开贵,周家启.配电网开关优化配置的改进遗传算法[J].电网技术, 2005(10): 29-19.

[3] 谢开贵,周家启.基于免疫算法的配电网开关优化配置模型[J].电力系统自动化, 2003(3):27-15.

[4] 程晓荣,张秋亮, 智慧,等.基于人工鱼群算法的配电网开关优化配置[J].华东电力，2008(1):36-1.

[5] 葛少云,李建芳,张宝贵.基于二分法的配电网分段开关优化配置[J].电网技术, 2007(7):31-13.

[6] 沈晓东,刘俊勇,孙毅.改进的分步最优法在配电网开关配置中的应用[J].电力自动化设备, 2003, 23(12): 9-12.

[7] Allan RN, Billinton R, Sjarief I, et al. A reliability test System for education purposes-basic distribution system data and results[J]. IEE Trans. on Power System, 1991, 6(2): 813-820.

收稿日期：（2015-12-03）