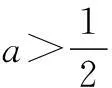不可忽视的非等价转化解题



不可忽视的非等价转化解题

甘志国

(北京市丰台区二中，100071)

等价转化思想是一种重要的数学思想.在解题中的作用往往体现在化复杂为简单、化陌生为熟悉,并且通过等价转化得到的结果是不需要检验的.

但在数学解题中,有很多情形不易、不宜、甚至是不可能进行等价转化(比如,解超越方程、解超越不等式、由递推式数列通项公式等等),这时只有“退而求其次”,可以考虑用非等价转化的方法来解题.常见的方法有“先必要后充分”和“先充分后必要”.

下面通过例题的解答来阐述这两种解题方法.

一、先必要后充分

分析若用等价转化来求解,就要对f(-x)=-f(x)等价变形,再由恒等关系式求出正常数a的取值范围.其中的运算量较大且复杂.

用“先必要后充分”的方法，只要注意奇函数的定义域关于原点对称,由f(x)的定义域是(-∞,log2a)∪(log2a,+∞),立即得到f(x)为奇函数的必要条件是log2a=0,a=1.

验证后易知当a=1时,函数f(x)是奇函数，所以所求a的取值范围是{1}.

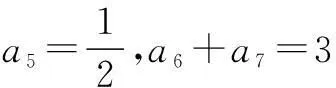
可得a1+a2+…+an>a1a2…an,即

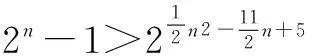
①

接下来如用等价转化则不易求出其解集，这里可先用不等式适当放缩找出①成立的必要条件，再验证极端情形求出n的最大值.

由①可得

n≤12.

易验证n=12时① 成立(即212-1>11成立),所以，满足题设的最大正整数n的值为12.

例3(2012年全国高考题)设函数f(x)=ex-ax-2.

(1)求f(x)的单调区间;

(2)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.

解(1)减区间是(-∞,lna),增区间是(lna,+∞).

(2)由题设可得xex-kex+k+1>0(x>0)恒成立.

接下来,若再进行等价转化(比如分离常数后求相应函数的最值),可能不易解决(因为求最值时需要求导函数的零点,很可能求不出来).但我们可以运用“先必要后充分”的方法来求解.

下面验证k=2时成立:

设g(x)=xex-2ex+3(x>0),则

g′(x)=(x-1)ex(x>0).

易见g(x)min=g(1)=3-e>0.

所以，所求k的最大值是2.

例4设f(x)=a2lnx-x2+ax(a>0).

(1)求函数f(x)的单调区间;

(2)求使e-1≤f(x)≤e2对x∈[1,e]恒成立的实数a的取值范围(其中e为自然对数的底).

解(1)可得

当x变化时,f′(x),f(x)的变化情况如下表所示:

x(0,a)a(a,+∞)f'(x)+0-f(x)↗极大值↘

所以，函数f(x)的单调增区间是(0,a),减区间是(a,+∞).

(2)若对题设“e-1≤f(x)≤e2对x∈[1,e]恒成立”进行等价转化,则须求出函数f(x)在区间[1,e]上的最大值和最小值,就须对参数a进行分类讨论,解法会很复杂.

但我们可以运用“先必要后充分”的方法来求解.

由题设,可得f(1)=a-1≥e-1,a≥e.

再由函数f(x)在[1,e]上递增,所以

e-1≤f(x)≤e2对x∈[1,e]恒成立

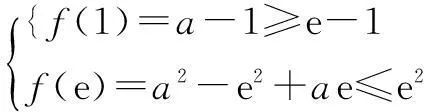
⟺a=e,

所以，所求实数a的取值范围是{e}.

例5(2013年全国高考题)已知函数f(x)=x2+ax+b,g(x)=ex(cx+d).若曲线y=f(x)和y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.

(1)求a,b,c,d的值;

(2)若x≥-2时,f(x)≤kg(x),求k的取值范围.

解(1)a=4,b=c=d=2(过程略).

(2)若对题设“当x≥-2时,f(x)≤kg(x)恒成立”进行等价转化,则需分离常数并分类讨论,求相应函数的最大值或最小值,过程会较复杂.

但我们可以运用“先必要后充分”的方法来求解.

由(1)知

f(x)=x2+4x+2,g(x)=(2x+2)ex.

由x=-2时f(x)≤kg(x)成立,得k≤e2；由x=0时f(x)≤kg(x)成立,可得k≥1.

所以，题设即为“x≥-2时h(x)=2kex(x+1)-x2-4x-2≥0(1≤k≤e2)恒成立”.

因h′(x)=2(x+2)(kex-1),令h′(x)=0,得x=-lnk(1≤k≤e2).

进而还可得:函数h(x)(x≥-2)的最小值h(-lnk)=(2-lnk)lnk≥0,所以所求k的取值范围是[1,e2].

二、 “先充分后必要”

下面谈谈用导数求解一类参数取值范围问题的好方法——“先充分后必要”.

例6(2006年全国高考题)设函数f(x)=(x+1)ln(x+1).若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.

解设g(x)=f(x)-ax=(x+1)ln(x+1)-ax(x≥0),原题设即g(x)≥g(0)=0(x≥0)恒成立.

当g(x)(x≥0)是增函数即g′(x)≥0(x≥0)恒成立时满足题设.

因g′(x)=ln(x+1)+1-a(x≥0),且g′(x)(x≥0)是增函数,所以当g′(0)=1-a≥0，即a≤1时满足题设.

当a>1时,得g′(x)的零点为ea-1-1,且当x∈(0,ea-1-1)时,g′(x)<0,即g′(x)在(0,ea-1-1)上是减函数,得g(x)

所以，所求a的取值范围是(-∞,1].

评注例6这种题型——“用导数求解一类参数取值范围问题”在高考题中很常见,其解答方法——“先充分后必要”也是一种容易掌握的好方法;而用“常规”的等价转化即分离常数法后再求相应函数的最值却难以求解.

下面再举两例谈谈这种题型及其解法.

题设即g(x)>g(0)=0(0

当g(x)(00恒成立，也即k≤2时满足题设.

综上，所求k的最大值为2.

例8(2010年全国高考题)设函数f(x)=ex-1-x-ax2,若当x≥0时,f(x)≥0,求a的取值范围.

解题设即f(x)≥f(0)=0(x≥0)恒成立.

所以，当f(x)(x≥0)是增函数，即f′(x)≥0(x≥0)恒成立时满足题设.

因f′(x)=ex-1-2ax，f′(0)=0,

所以，当f′(x)(x≥0)是增函数，即f″(x)≥0(x≥0)恒成立时满足题设.