解题巧用特殊值 柳暗花明有捷径
2016-03-30马俊,李青林
○高考之窗○
解题巧用特殊值柳暗花明有捷径
马俊李青林
(湖北省武汉市华中科技大学附属中学,430074)
在高三数学复习中,解题技巧和解题策略是学生要着重培养的能力.对于不少试题,求解时运用特殊值法常常是一个不错的选择,它往往会给我们带来惊喜.虽然学生对这个方法并不陌生,但很多学生在特殊值法的运用上却没有较深的认识,甚至还存在一定的误区.为此,笔者对特殊值法的运用进行了整理,与各位读者共享.
一、细心寻差异,特值定选项
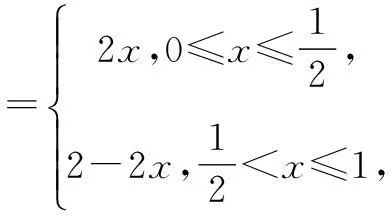
(A)2n-1(B)2n-1
(C)2n(D)n2
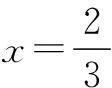
评注这是一道创新题,属于高考中常见的题型,n如果用常规方法来处理,不仅小题大做,而且相当困难.但是细心的学生通过观察选项可以发现n=1时可以判断C选项是否正确,而n=2时A,B,D选项均不相同,因此n只需取1和2便能得出结果.
二、条件特殊化,解题有方法
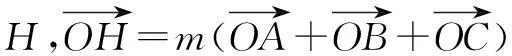
(A)-1(B)1(C)-2(D)2
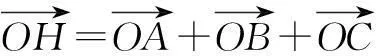
评注如果使用常规方法,选取一般三角形,显然外心与垂心位置的确定就是一个难点,因此将条件特殊化后,外心和垂心的位置也具有了特殊性,分析起来十分容易.这里还可以思考一下,为什么不取等边三角形这个特殊的情况.
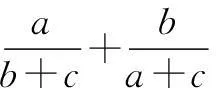
解不妨设∆ABC是等边三角形,结果为1.
评注这种思路往往适用于选择题及答案具有唯一确定性的填空题.当所给的条件具有一般性的时候,可以尝试着将条件特殊化来进行解答.不仅可以避免一些分类的讨论,也可以使用特殊情况下所具有的一些结论和性质来解题,快速得出结果.
三、特值引猜想,理清解题思路
例4已知函数f(x)=ex,x∈R.
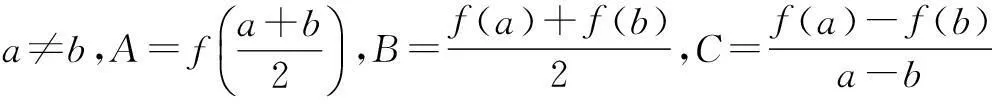
解不妨设a=0,b=1,则
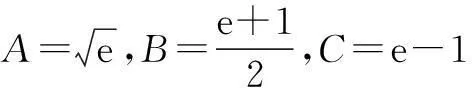
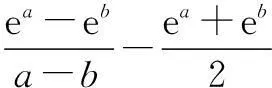
2(ea-b-1)-(a-b)(ea-b+1)<0.
设x=a-b>0,即证
F(x)=2(ex-1)-x(ex+1)<0
在x∈(0,+∞)时恒成立.
又F′(x)=ex-1-xex.
设t(x)=ex-1-xex,则
t′(x)=-xex<0,
故t(x) 即F(x)在x∈(0,+∞)上是减函数,所以F(x) 同理可证A 评注此题考查的是函数的的凹凸性与斜率之间大小的比较,显然在大小关系已知的情况下去证明,不仅目标明确,并且可以避免一些不需要证明. 分析如何探明点T的位置是本题求解的关键.若直线m的斜率不存在,则以AB为直径的圆为 x2+y2=1; ① 若直线m的斜率为0,此时以AB为直径的圆为 ② 由①,②联立知,若点T存在,则其坐标只能是(0,1). (18k2+9)x2-12kx-16=0, 评注通过对一些特殊值或是特殊情况的分析,寻找规律或是解题目标,然后提出猜想,最后对猜想进行证明.特别是与数学归纳法综合时,这种思路的价值体现得更为明显. 四、特值缩范围,巧妙扔包袱 解由题意,得 评注用分类讨论的常规思想解答这道题时较为复杂.上面用特殊值法有效地缩小了a的范围,减少分类讨论的情况,扔掉了一个繁、杂的“大包袱”,并且“猜”的这个特殊值x=1可以说是恰到好处.x=1是如何“猜”出来的呢,x=1不仅好算,而且g′(1)=0具有的特殊性也是学生能够体会到的. (1)解关于x的不等式 (2)若常数k是正整数,当x>0时, 恒成立,求k的最大值. 解(1)略. (x+1)ln(x+1)+1-2x>0 恒成立. 令g(x)=(x+1)ln(x+1)+1-2x,则 g′(x)=ln(x+1)-1. 当x∈(0,e-1)时,g′(x)<0;当x∈(e-1,+∞)时,g′(x)>0, 故g(x)≥g(e-1)=3-e>0,所以正整数k的最大值为3. 评注在一些恒成立问题求参数范围的题型中,由于参数的范围过大,导致分类讨论十分复杂.这时可以尝试使用特殊值法寻找恒成立问题的必要条件,从而缩小参数的范围,降低解题难度. 此外,在部分学生心中存在着特殊值法只能做小题的误区,这是因为对特殊值法的理解不够深刻.完成大题时,特殊值法求解出来的是必要条件,不能直接用来得出结果或是结论,必须在其基础上进行充分性的证明.因此,只有体会了“大题小做”的思想,对特殊值法才会有一个更深的认识. 特殊值法的好与妙是学生所能认同的,但特殊值法绝不是仅仅通过几个特殊的数或特殊的条件来解题的方法,必须上升到数学思想的层面上去认识他,才能够在实际使用给我们带来柳暗花明的惊喜.