数学“微课”初探——以“导数的概念”一课为例
2016-03-30王强
数学“微课”初探
——以“导数的概念”一课为例
王强
(江苏省常州市第二中学,213003)
微课,又名微课程,是相对常规课来说的一种微小的课程.授课时间一般控制在5-10分钟,用以讲授单一知识点或突破某个教学问题.在我国,微课的概念是由胡铁生率先提出的,在他看来,“微课”是按照新课程标准及教学实践要求,以教学视频为主要载体,反映教师在课堂教学过程中针对某个知识点或教学环节而开展教与学活动的各种教学资源的有机组合.微课的制作不存在技术上的壁垒,决定微课的成败应该是教学设计.微课面对的对象是学生个体,因而微课的教学设计要立足于满足学生个性化学习的需要.
本节微课是(苏教版)高中数学选修2-2第一章1.1.2瞬时变化率——导数的内容,主要介绍导数的概念.本文从微引入、微探究、微例题、微小结四个方面,设计了导数的概念这节微课,阐述了怎样借助信息技术设计数学微课,优化课堂效率.
一、教学需求分析
1. 适用对象分析
适用对象是已经学习了平均变化率和了解物理上的平均速度和瞬时速度的高二学生.学生已经学习了平均变化率,这节课在探究中要求平均速度的问题难度不大,于是笔者设计了直接用Excel表格的批量计算功能进行计算.因为上节课学生接触了曲线上一点处的切线,体会了以直代曲的逼近方法,与本节课当时间间隔很短,所以利用平均速度估计瞬时速度的方法,有效化解了这节课的难点.
2. 学习内容分析
导数的概念是(苏教版)高中数学选修2-2第一章1.1.2瞬时变化率——导数中的内容.本节书上设置了3个部分,一是曲线上一点处的切线;二是瞬时速度与瞬时加速度;三是导数. 课本上是在学生学习了物理的平均速度和瞬时速度的背景下,以及前节课所学的平均变化率基础上,从跳水问题出发通过用平均速度估计瞬时速度;利用从特殊到一般的研究方法,将一般的速度问题推广到变化率问题,从而得到瞬时变化率即导数的概念,为以后更好地研究导数的几何意义和导数的应用奠定基础.
3.教学目标分析
(1)课标要求分析
通过对大量实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,知道瞬时变化率就是导数,体会导数的思想及其内涵.
(2)三维教学目标分析
知识与技能:通过实例的分析,经历由平均速度过渡到瞬时速度的过程,了解导数概念的实际背景,理解导数的概念.
过程与方法:通过导数概念的形成过程,体验逼近、类比、从特殊到一般的数学思想方法.
情感、态度与价值观:通过研究实际的跳水问题,培养学生数学的应用意识,增强学习数学的兴趣.
(3)教学重、难点分析
重点:导数概念的形成,导数内涵的理解
难点:在平均变化率的基础上去探求瞬时变化率,深刻理解导数的内涵.
4.教学方法分析
(1)教法分析
通过研究某区间上的平均速度→Δt取比较小的值时的平均速度→观察发现平均速度趋近于一个常数→将结论推广→瞬时变化率→导数的概念.
(2)学法分析
在教师的指导下,通过认真观察分析数据,发现规律,利用特殊到一般的方法进行推广.
(3)教学用具分析
整节课借助多媒体进行辅助教学,首先借助田亮奥运会夺金的跳水视频引入,激发大家的兴趣;过程中在平均速度的计算上借助了Excel进行处理,节省时间.
二、教学设计
1.创设情境
微课题目是《导数的概念》,首先请欣赏田亮悉尼奥运会10 m高台跳水的精彩瞬间.
在10 m高台跳水运动中,假设某运动员相对水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
h(t)=-4.9t2+6.5t+10.
问题1计算运动员在1≤t≤1.1这段时间里的平均速度,
问题2如何通过平均速度来求运动员的瞬时速度呢?如t=1 s时刻的瞬时速度?
我们容易想到为了使平均速度更好地表示瞬时速度,应该使时间间隔尽量小.
从跳水问题出发去计算平均速度,并提出如何通过平均速度求瞬时速度.在学生讨论交流基础上,提出:当时间间隔很小的时候,平均速度就会逼近瞬时速度.
设计意图从跳水问题出发去计算平均速度,并提出如何通过平均速度求瞬时速度;在学生讨论交流基础上,提出:当时间间隔很小的时候,平均速度就会逼近瞬时速度.
2.概念形成


教师借助Excel展示计算结果如下:
表1:时间t从大于1的一边趋近于1时

时间区间Δt平均速度[1,1.1]0.1-3.79[1,1.01]0.01-3.349[1,1.001]0.001-3.3049[1,1.0001]0.0001-3.30049[1,1.00001]0.00001-3.300049[1,1.000001]0.000001-3.3000049[1,1.0000001]0.0000001-3.300000486[1,1.00000001]0.00000001-3.299999918[1,1.000000001]0.000000001-3.300000273
设计意图学生对概念的认识需要借助大量的直观数据,通过Excel的批量计算功能让学生直观感受时间从左边或右边逼近1s时,平均速度有怎样的变化趋,从而化解这节课的难点.
表2:时间t从小于1的一边趋近于1时

时间区间Δt平均速度[0.9,1]-0.1-2.81[0.09,1]-0.01-3.251[0.009,1]-0.001-3.2951[0.0009,1]-0.0001-3.29951[0.00009,1]-0.00001-3.299951[0.000009,1]-0.000001-3.2999951[0.0000009,1]-0.0000001-3.299999509[0.00000009,1]-0.00000001-3.300000095[0.000000009,1]-0.000000001-3.300000273
问:当Δt趋近于0时,平均速度有怎样的变化趋势?
小结:当Δt趋近于0时,平均速度趋近于常数-3.3.这个常数可作为运动员在t=1s时刻的瞬时速度.
问题4一般地,运动员在某个时刻t0的瞬时速度如何表示呢?

设计意图通过类比来定义t0时刻的瞬时速度,体现了特殊到一般的思维方法.
问题5瞬时速度可以看成位移对于时间的瞬时变化率.如果将高台跳水问题中的函数用f(x)来表示,那么函数f(x)在x=x0处的瞬时变化率如何表示呢?


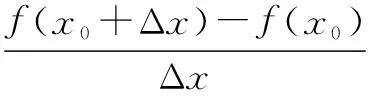
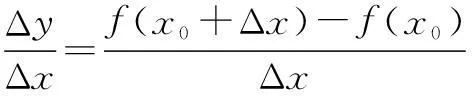
设计意图引导学生舍弃具体问题的实际意义,抽象得到导数定义.由浅入深,帮助学生完成了思维的飞跃.
3.巩固应用
例利用导数的定义求f(x)=x2+2在x=1处的导数.

设计意图发展学生的应用意识,进一步加深对导数概念的理解及应用.
4.归纳小结
(1)知识概念:
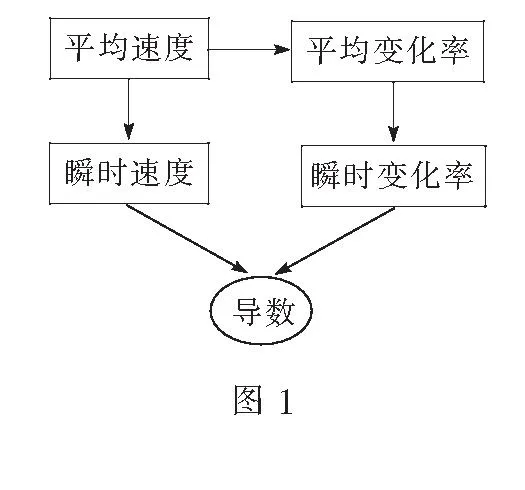
(2)思想方法:逼近、类比,从特殊到一般.
设计意图不仅仅总结知识,更重要的是总结数学思想方法.
三、学习指导
自学视频的基础上能够解决两个问题:一是导数的概念是如何形成的?用了什么数学思想方法?(具体的可参考归纳小结).二是如何利用导数的定义求给定函数在某点的导数.在看懂微课例题的基础上,尝试解决下面的练习.
练习(满足个性化学习的需求):
(1)求下列函数在已知点处的导数:
(i)y=3x+1,x=3;(ii)y=x2,x=a;

(2) 航天飞机发射后的一段时间内,第t(s)时的高度h(t)=5t3+30t2+45t+4,其中h的单位为m,t的单位为s.
(i)h(0),h(1)分别表示什么?
(ii)求第1s内的平均速度;
(iii)求第1 s末的瞬时速度?
(iv)经过多长时间,飞机的速度可达到75 m/s?
四、配套学习资料(介绍导数发展史)
大约在1629年,数学家费马研究了作曲线的切线和求函数极值的方法;1637年左右,他写一篇手稿《求最大值与最小值的方法》.在作切线时,他构造了差分f(A+E)-f(A),发现的因子E就是我们所说的导数f′(A).
17世纪生产力的发展推动了自然科学和技术的发展,在前人创造性研究的基础上,大数学家牛顿 、莱布尼茨从不同的角度开始系统地研究微积分.牛顿的微积分理论被称为“流数术”,他称变量为流量,称变量的变化率为流数,相当于我们所说的导数.牛顿的有关“流数术”的主要著作是《求曲边形面积》、《运用无穷多项方程的计算法》和《流数术和无穷级数》.流数理论的实质概括为:他的重点在于一个变量的函数而不在于多变量的方程;在于自变量的变化与函数的变化的比的构成;在于决定这个比当变化趋于零时的极限.

1823年,柯西在他的《无穷小分析概论》中定义导数:如果函数y=f(x)在变量x的两个给定的界限之间保持连续,并且我们为这样的变量指定一个包含在这两个不同界限之间的值,那么是使变量得到一个无穷小增量.19世纪60年代以后,魏尔斯特拉斯创造了ε-δ语言,对微积分中出现的各种类型的极限重加表达,导数的定义也就获得了今天常见的形式.
五、制作技术介绍
(1)Excel填充柄用法:把鼠标挪到单元格右下角,当鼠标变成十字时,按住往下或往右拖动,就可以将单元格往下填充,或往右填充,实现批量计算的功能.
(2)如何利用Camtasia Studio 截视频时出现只有声音没有图像的问题的解决方法:右击电脑桌面的属性,点设置,点高级,点疑难解答,然后将硬件加速调到无,然后就可以用直接打开Camtasia Studio的录制屏幕功能截屏了,此时会既有声音,也有图像.
(本文系江苏省教育科学“十二·五”规划2015年度课题“e学习环境下高中课堂教学变革的实践研究”(课题编号:D/2015/02/038)的阶段性研究成果)
