浅议高考数学第二轮复习——以一道课本习题的深入探究为例



浅议高考数学第二轮复习
——以一道课本习题的深入探究为例

兰声波

(四川省沐川中学校 ，614599)

高考数学第二轮复习的目的是:

(1)巩固.把巩固基础知识、基本技能、基本方法、基本经验放在首位,形成扎实的基础.

(2)完善.进一步完善知识体系,着意于数学思想与方法的明朗化,进一步认识和挖掘知识之间相互交融后所产生的“生成性知识”,并强化其教学,实现更高层次的系统化.

(3)综合.适当增强知识的联接点,题目的综合性和灵活性,以达到培养综合能力的要求．

下面，笔者给出人教版高中数学必修1第25页第3题:

函数f(x)=[x],[x]表示函数值不超过x的最大整数.例如:[-3.5]=-4,[2.1]=2,当x∈[-2.5,3)时,写出函数f(x)的解析式,并作出函数的图象.

(1)巩固.由学生再做这道习题,复习分段函数,培养基本作图的能力．

作出图象(如图1).

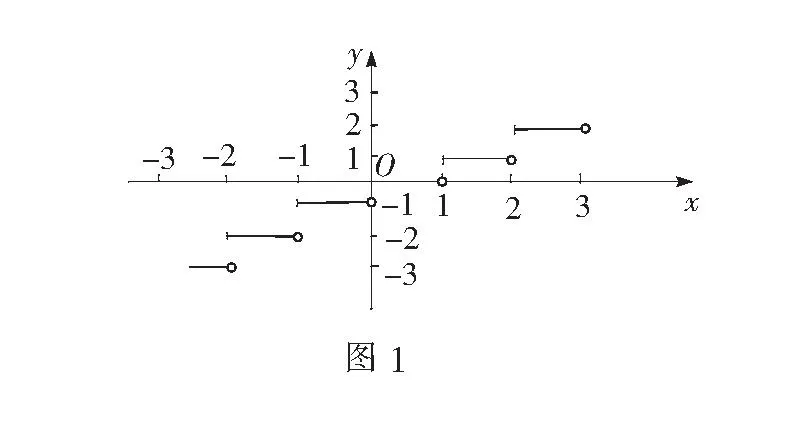
(2)完善.由学生完成以下问题,从而深刻理解“取整”函数及其变化的性质、特点．

问题1若[x+1]=3，求x的取值范围.

解∵[x+1]=3,∴3≤x+1,

∴2≤x<3.

问题2[x1]>[x2]是x1>x2的()条件.

(A)充分不必要

(B)必要不充分

(C)充要

(D)既不能充分也不必要

问题3定义:f(x)={x}=x-[x],画出f(x)={x}的图象,结合图象回答f(x)的值域、最小正周期、单调递增区间并计算f(2015.3)+f(-15.3).

作出图象(如图2)，解答.

(3)综合.把“取整”函数与直线、数列、二项式定理联系起来,使知识“立体化”培养学生思维的灵活性,发散性．

问题4设函数

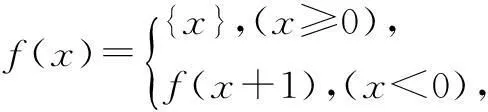
且方程f(x)=kx+2k(k>0)仅有三个不同的实数根,求k的取值范围.

解设y=f(x)和y=g(x)=k(x+2)(k>0).

∵方程f(x)=kx+2k(k>0)仅有三个不同的实数根，

∴直线g(x)=k(x+2)与y=f(x)的图象仅有三个交点,

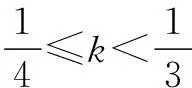
解设区间[i-1,i)内f(x)的值域的元素个数为bi,i∈N*.

当x∈[0,1)时，f(x)=0,∴b1=1；

当x∈[1,2)时，f(x)=[x·1]=1,∴b2=1；

当x∈[2,3)时，f(x)=[2x]， 而2x∈[4,6),∴f(x)∈{4、5},∴b3=2,

以此类推，

x∈[n-1,n)时，bn=n-1.

∴当x∈[0，n)时,

an=1+2+3+…+n-1

当且仅当n=8时取“=”，即

+…+

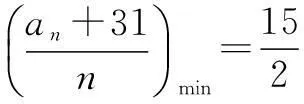
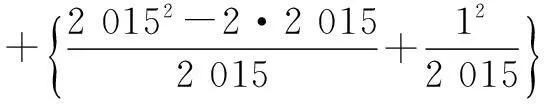
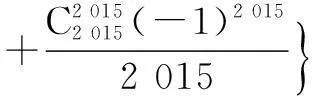
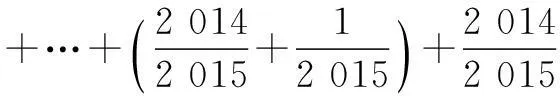
由以上的分析可见,教师在教学中,要注意深入钻研教材,研究课本例题、习题、引导学生回归教材.对课本例、习题进行研究、探讨,充分发挥课本的功能,从而提高学生的解题能力,培养学生的数学思维和创新意识．