动车运用所调车作业计划编制优化
2016-03-30郭小乐黎浩东陈胜波刘星材
郭小乐,宋 瑞,黎浩东,陈胜波,刘星材
(北京交通大学 交通运输学院,北京 100044)
动车运用所调车作业计划决定了动车运用所内动车组各项检修作业的起始、终止时刻以及占用的作业线。合理的动车运用所调车作业计划可以避免或减少动车组因等待而造成的延误,从而尽量避免动车组因不能及时完成维修作业而对动车组运用计划造成影响。
部分学者对于该问题及相关问题进行了研究。文献[1]以股道联通关系、股道时空占用相容性等为约束,以减少关键线区占用时间和调车路径费用为优化目标建立优化模型,运用最大最小蚁群算法进行求解。文献[2]针对动车运用所存车线运用方案进行了研究,以给定动车组占用存车线时间为前提,以提高存车线利用率和减少调车作业走行距离为优化目标,以列位占用相容性条件为约束建立优化模型,运用模拟退火算法求解模型。文献[3—6]研究了车站股道的运用问题,多以资源的时空占用相容性为约束,以列车对股道的占用情况为决策变量,采用启发式算法对模型进行求解。文献[7—12]研究了车间作业调度(Job Shop Scheduling)问题,均采用智能算法进行求解。目前针对动车运用所调车作业计划编制问题,在各项作业的执行顺序不确定的情况下综合考虑各类作业线运用方法的研究还比较少,实际工作中的调车作业计划多为人工编制,如果动车运用所内的动车组数量较多,人工编制调车作业计划的方法将难以满足作业要求。
本文针对动车运用所调车作业计划编制问题,以作业线数目、动车组数目以及动车组执行各项作业的顺序和占用作业线的时间为约束条件,以动车运用所内动车组总延误时间最小为目标函数,建立动车运用所调车作业计划编制优化模型,设计求解该模型的微进化算法及启发式规则;并用算例验证模型和算法的有效性和正确性。
1 动车运用所调车作业计划编制问题描述
解决动车运用所调车作业计划编制问题就是如何在动车运用所各类作业线数量一定的情况下,合理安排动车组的各项检修作业,优化作业流程。
动车运用所调车作业计划编制问题与工厂车间的作业调度问题相似。可以将等待作业的动车组看作等待进行加工的工件,将作业看作机器。但是与车间调度问题不同的是,动车组执行作业的次序是不确定的,在各种类型作业线上停留的时间也是不确定的,并且动车组为完成某项作业必须始终处于某类作业线上,而车间调度问题中的工件则不必始终处于某台机器上。
以尽头式布局的动车运用所的一级修调车作业计划编制问题为例,一级修包括检修、清洗、转线、存车4项作业,该种情形下动车组完成各项作业的顺序不定,其中检修和清洗2项作业是必须执行的,转线作业可与其他3项作业中的任一项合并,存车作业只有在以下4种情况下需要执行。
(1)动车组到达动车运用所时检修线、清洗线全部被占用;
(2)动车组完成检修作业而要进行清洗作业时,清洗线全部被占用;
(3)动车组完成清洗作业而要进行检修作业时,检修线全部被占用;
(4)动车组完成检修、清洗作业的时刻早于规定的离开动车运用所的时刻。
所以动车组在存车线上的停留时间并不确定。而且当动车组完成检修作业或清洗作业但无法转线时(如尚未执行作业的作业线全部被占用),动车组必须在当前作业线上等待转线,所以动车组在检修线和清洗线上的停留时间也不确定。
2 动车运用所调车作业计划编制优化模型
以动车运用所的一级修调车作业计划编制问题为例,构建动车运用所调车作业计划编制优化模型。
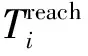
对于动车运用所调车作业计划的编制问题,需要决策的变量如下。
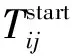

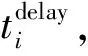
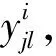
根据上述分析,以最小化动车运用所内所有动车组的总延误时间T为目标函数,构建如下动车运用所内调车作业计划编制优化模型。
(1)
s.t.
i=1,2,…,n;j=1,2,…,m;f∈Fj
(2)
i=1,2,…,n;j=1,2,…,m
(3)
i=1,2,…,n;j=1,2,…,m
(4)
i,k=1,2,…,n;j=1,2,…,m;f∈Fj
(5)
i=1,2,…n;j,l=1,2,…,m
(6)
j=1,2,…,m
(7)
(8)
i=1,2,…,n;j=1,2,…,m
(9)
i=1,2,…,n;l=1,2,…,m
(10)
i=1,2,…,n;j=1,2,…,m
(11)
i,k=1,2,…,n;j,l=1,2,…,m
(12)
模型中的约束条件:式(2)为作业线f上的动车组维修顺序约束;式(3)为动车组Di执行各项作业的顺序约束;式(4)为动车组Di完成作业Yj的开始、结束时刻关系约束;式(5)为不同动车组在作业线f上的作业时间关系约束,即如果动车组Dk紧随动车组Di在作业线f上作业,则动车组Dk执行作业Yj的开始时刻不早于动车组Di执行作业Yj的结束时刻;式(6)为动车组Di执行不同作业的作业时间关系约束,即对于动车组Di,如果作业Yl紧跟在作业Yj之后,则动车组Di执行作业Yl的开始时刻不早于动车组Di执行作业Yj的结束时刻;式(7)为作业线数量约束;式(8)为动车组数量约束;式(9)为最晚完工时刻约束;式(10)为各非虚拟动车组执行各非虚拟作业所用时间约束;式(11)为作业最早开始时刻约束。
3 模型求解算法
通过以上对动车运用所调车作业计划编制问题的分析可知,编制1个完整的动车运用所调车作业计划需要解决以下2个问题。
(1)确定每列动车组执行每项作业的起、止时刻。
(2)确定每列动车组执行每项作业需要占用的作业线。
因此对应地将模型分2个阶段求解:第1阶段,采用微进化算法求解每列动车组执行每项作业的起、止时刻,进而通过计算该列动车组执行最后一项作业的结束时刻与动车运用所运用计划规定的出所时刻之差求得该列动车组的延误时间,最终求得全部动车组的总延误时间;第2阶段,采用启发式规则求解每列动车组执行各项作业所占用的作业线。
微进化算法是一种新型智能优化算法,它模拟的是生物种群中的个体向种群中的优秀个体学习的过程,并且该算法涉及的参数较少,便于实现,可以有效求解各动车组执行各项作业的起止时刻。已经有学者将微进化算法应用于函数优化问题[13]和实际工程问题[14],取得了良好效果。
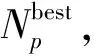
(13)
式中:θ是一个服从期望为0、标准差为δ的正态分布的随机数。
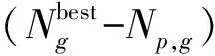
3.1 个体编码方式
需要说明以下几点。
(1)由于列车从到达动车所到离开动车所始终处于3项作业中某一项作业的作业线上,所以下一项作业的作业开始时刻与上一项作业的作业结束时刻相同。
(2)3项作业的开始时刻中必须有1项作业的开始时刻与列车到达动车所的时刻相同。
(3)所有作业的结束时刻必须不早于动车组运用计划规定的最晚完工时刻。
(4)检修作业和清洗作业的作业时间均不能小于其标准作业时间。
3.2 作业起、止时刻方案的可行性判断
由于图1所示的编码方式无法保证调车计划中某一时刻每条作业线上至多停放1列动车组,即不能确保调车作业计划是可行的,因此引入“时段”的概念。“时段”为某开始时刻和某结束时刻之间的一段时间。对于某项作业,如果有2列动车组执行该项作业的时段存在重叠部分,则说明在该重叠部分表示的时段内这2列动车组在同时执行该项作业,如图2所示。
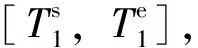
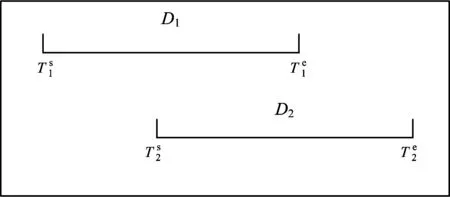
图2 时段
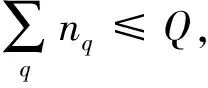
Step 1:初始化。定义变量K=0。令动车组索引i=1。
Step 2:对于动车组Di,定义时段ti=[Ts,Te],Ts和Te分别为动车组Di执行该项作业的开始与结束时刻。
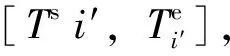
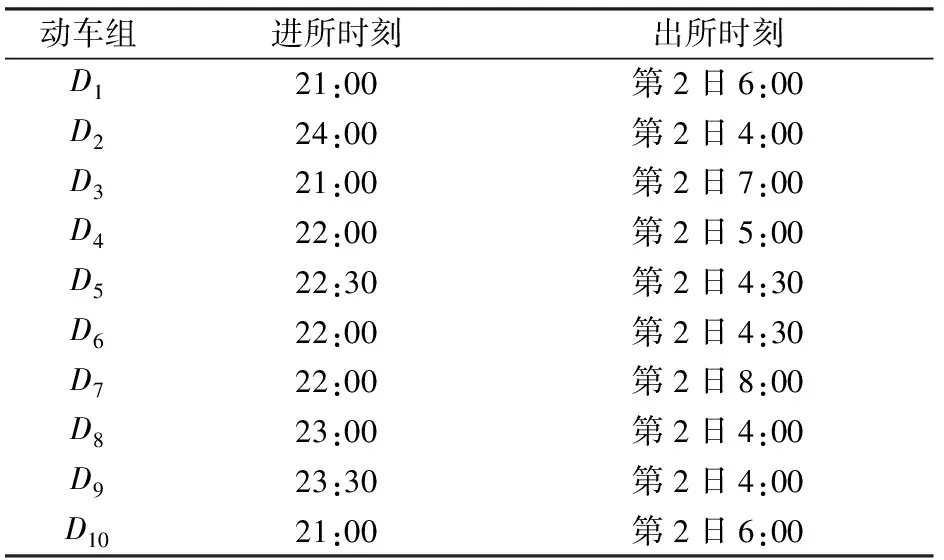
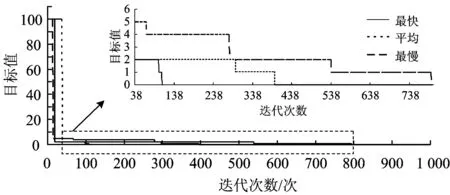
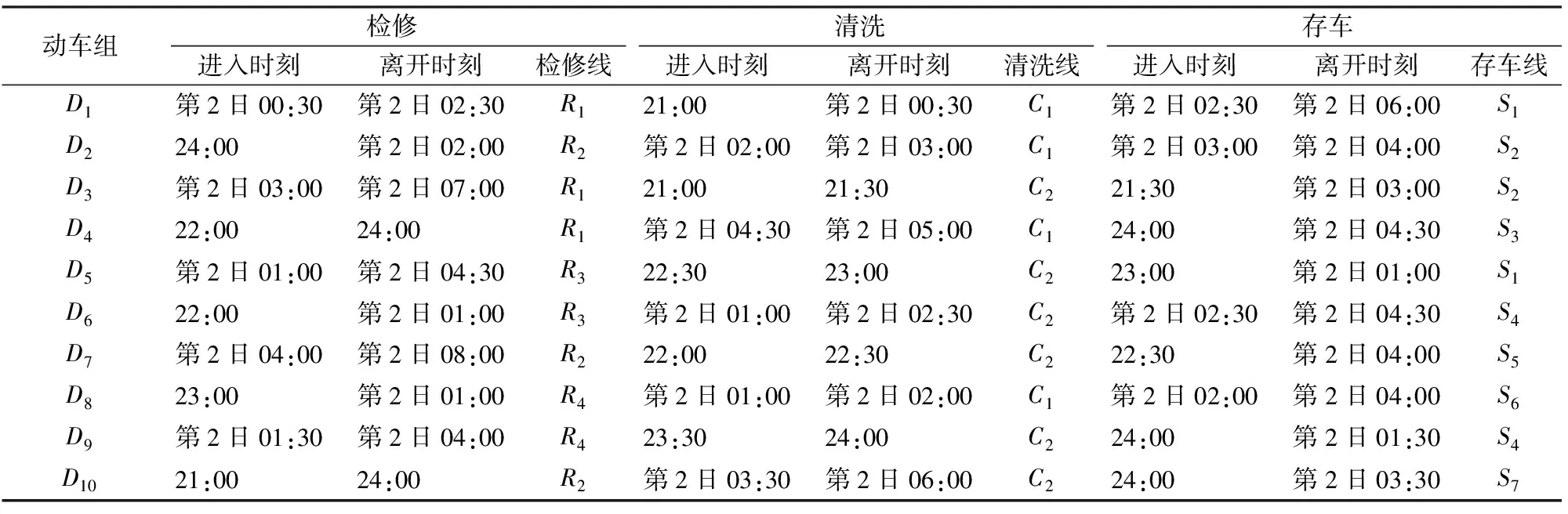
Step 4:如果i′ 按照上述规则分别检查检修、清洗和存车3项作业中是否存在重叠的时段,若对于每项作业,同时执行该作业的动车组数均不超过作业线数目Q,则该作业起止时刻方案是可行的,进而通过计算该列动车组执行最后一项作业的结束时刻与动车运用所运用计划规定的出所时刻之差得到该列动车组的延误时间,最终求得全部动车组的总延误时间。计算过程中,允许不可行解的存在。对于不可行解,给予其一定的惩罚值。 采用式(14)更新个体状态: (14) 个体状态更新后,如果3项作业中没有任何1项作业的开始时刻与动车组的到达时刻相同,则随机选择1项作业,令其开始时刻与动车组的到达时刻相同。 作业起止时刻方案和总延误时间计算步骤如下。 Step 1:初始化。令g=0,确定种群规模Z和最大迭代次数,初始化种群,得到每列动车组的作业顺序及各作业起止时刻的初始方案。 Step 3:种群进化。对于第g代种群,按照式(14)更新种群中每个个体的状态,产生第g+1代种群。需要说明的是,更新状态后,个体中各动车组3项作业的开始时刻必须有1项作业的开始时刻与列车到达动车所的时刻相同。 作业线分配算法实际上是一组规则,按照这组规则,可以在保证无多列动车组同时占用某条作业线的前提下确定每列动车组执行各项作业所占用的作业线。具体算法步骤如下。 Step 1:初始化。对于某项作业,如果属于该项作业的作业线数目为Q,则定义Q个集合L1,L2,…,LQ。令i=0,j=1。 Step 2:令i=i+1。转Step 5。 Step 3:令j=j+1。 Step 4:对于动车组Di,检查该动车组执行该项作业的时段是否与Lj中已存在的动车组执行该项作业的时段存在重叠部分,如果不存在重叠部分,则将动车组Di放入Lj,转Step 2,否则转Step 3。 Step 5:检查是否已将所有动车组放入集合中,如果所有动车组都已放入集合中,则输出1个调车作业计划,终止算法;否则转Step 4。 假设某动车运用所为尽头式布局,共有4条检修线(R1-R4),2条清洗线(C1和C2)和10条存车线(S1-S10)。检修作业时间标准为2.0 h,清洗作业时间标准为0.5 h[1]。动车组运用计划见表1。 采用建立的模型和给出的算法,选取不同参数对算法进行测试。结果表明,种群规模Z在200~800范围内调整,正态分布随机数θ的标准差δ在0.7~1.0范围内调整,算法均能收敛至相同的最优解。 选取收敛至最优解所需运算时间最小的参数为:种群规模Z=200,最大迭代次数G=1 000,正态分布随机数θ的标准差δ=0.95,替换不可行个体的替换概率P=0.6。经过10次测算,收敛至最优解的平均计算时间为9.12 s。算法迭代图如图3所示。 表1 某动车运用所运用计划 图3 算法迭代图 图3给出了算法的最快、最慢和平均搜索过程,其中右上图是第38代至第800代的局部放大图。最小延误为0,最快在第108代收敛至最优解,最慢在第794代收敛至最优解。最终计算结果见表2。 表2 调车作业计划 由上可知,本文提出的模型与算法可以在较短时间内求得动车运用所调车作业计划的最优解,实现动车运用所内动车组总延误时间的最小(本算例中为0)。 在测试过程中,可以求得目标函数值相同(均为0,即总延误时间为0)的不同调车作业计划,这说明动车运用所调车作业计划存在多样性,不是唯一的。 本文以动车运用所内所有动车组的总延误时间最小为目标函数,以作业线数目、动车组数目以及动车组执行各项作业的顺序和占用作业线的时间为约束条件,构建了动车运用所调车作业计划优化模型,并用微进化算法和作业线分配算法对模型进行求解,通过迭代逐步得到了问题的最优解。算例的计算结果表明,通过该模型及算法可以实现动车运用所调车作业计划的自动编制,验证了模型及算法的有效性。 实际工作中,部分动车运用所的作业线为二列位设计,即1条作业线可以容纳1列长编组动车组或2列短编组动车组。对于这种情况,编制动车运用所调车作业计划还需要考虑动车组的长短编组因素,如何在构建模型时考虑动车组的长短编组情况将是今后研究的一个重点。 [1]王忠凯,史天运,张惟皎,等. 动车运用所调车作业计划优化编制模型与算法[J]. 铁道学报,2013,35(8):1-9. (WANG Zhongkai, SHI Tianyun, ZHANG Weijiao, et al. Model and Algorithm for Optimized Formulation of Scheduled Shunting Operation Plans of Electric Multiple Units Depots [J]. Journal of the China Railway Society, 2013, 35(8):1-9. in Chinese) [2]张惟皎,史天运,陈彦. 动车运用所存车线运用方案优化模型与算法[J]. 中国铁道科学,2013,34(1):121-125. (ZHANG Weijiao, SHI Tianyun, CHEN Yan. Optimization Model and Algorithm for the Operation Plan of the Stabling Track at EMU Running Shed [J]. China Railway Science, 2013, 34(1):121-125. in Chinese) [3]张英贵,雷定猷,刘明翔. 铁路车站股道运用排序模型与算法[J]. 中国铁道科学,2010,31(2):96-100. (ZHANG Yinggui, LEI Dingyou, LIU Mingxiang. Scheduling Model and Algorithm for Track Application in Railway Station [J]. China Railway Science, 2010, 31(2):96-100. in Chinese) [4]史峰,陈彦,秦进,等.铁路客运站到发线运用和接发车进路排列方案综合优化[J].中国铁道科学,2009,30(6):108-113. (SHI Feng, CHEN Yan, QIN Jin, et al. Comprehensive Optimization of Arrival-Departure Track Utilization and Inbound-Outbound Route Assignment in Railway Passenger Station [J]. China Railway Science, 2009, 30(6): 108-113. in Chinese) [5]CHEN Dingjun, NI Shaoquan, LI Chengbing, et al. Study on the Optimization Model of Utilization Scheme of Railway Passenger Station Tracks Based on an Improved ACO Algorithm [C]//Second International Conference on Intelligent Computation Technology and Automation. Changsha: IEEE, 2009:415-418. [6]吕红霞,何大可,陈韬. 基于蚁群算法的客运站到发线运用计划编制方法[J]. 西南交通大学学报,2008,43(2):153-158. (LÜ Hongxia, HE Dake, CHEN Tao. Method of Arrival and Departure Tracks Utilization Plan in Railroad Passenger Station Based on Ant Colony Algorithm [J]. Journal of Southwest Jiaotong University, 2008, 43(2):153-158. in Chinese) [7]SHEN Liji. A Tabu Search Algorithm for the Job Shop Problem with Sequence Dependent Setup Times [J]. Computers & Industrial Engineering, 2014, 78: 95-106. [8]HUANG X W, ZHAO X Y, MA X L. An Improved Genetic Algorithm for Job-Shop Scheduling Problem with Process Sequence Flexibility [J]. International Journal of Simulation Modelling, 2014, 13(4): 510-522. [9]MEERAN S,MORSHED S. A Hybrid Genetic Tabu Search Algorithm for Solving Job Shop Scheduling Problems: A Case Study [J]. Journal of Intelligent Manufacturing, 2012, 23:1063-1078. [10]GIOVANNI L D E, PEZZELLA F. An Improved Genetic Algorithm for the Distributed and Flexible Job-Shop Scheduling Problem [J]. European Journal of Operational Research, 2010, 200: 395-408. [11]CHANDRASEKARAN M, ASOKAN P, KUMANAN S, et al. Solving Job Shop Scheduling Problems Using Artificial Immune System [J]. The International Journal of Advanced Manufacturing Technology, 2006, 31:580-593. [12]PONNAMBALAM S G, ARAVINDAN P, RAJESH S V. A Tabu Search Algorithm for Job Shop Scheduling [J]. The International Journal of Advanced Manufacturing Technology, 2000, 16:765-771. [13]许小健,查日兴. 一种新型群体智能优化算法——微进化算法[J]. 厦门理工学院学报,2010,18(3):38-42. (XU Xiaojian, ZHA Rixing. Microevolution Algorithm: a New Swarm Intelligent Optimization [J]. Journal of Xiamen University of Technology, 2010, 18(3):38-42. in Chinese) [14]彭汝发,许小健. 用微进化算法反演岩石蠕变模型非定常参数[J]. 长江科学院院报,2011,28(6):50-54. (PENG Rufa, XU Xiaojian. Microevolution Algorithm for Inversion of Non-Stationary Parameters in Rock Creep Model [J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(6):50-54. in Chinese)3.3 个体状态的更新方式

3.4 作业起止时刻方案和总延误时间计算方法
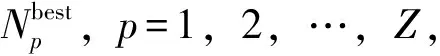
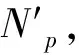
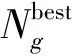
3.5 作业线分配算法
4 算例分析
5 结 语
