浮置板轨道动力响应分析的广义波数法
2016-03-30刘维宁马龙祥姜博龙王文斌
刘维宁,马龙祥,姜博龙,王文斌
(1.北京交通大学 土木建筑工程学院,北京 100044;2.西南交通大学 土木工程学院,四川 成都 610031;3.西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031;4.中国铁道科学研究院 城市轨道交通中心,北京 100081)
近年来,浮置板轨道由于良好的减振性能,在轨道交通领域得到了广泛的应用。对其动力特性及减振性能的研究也成了众多业内研究人士关注的热点[1-8]。
目前,对该轨道的主要研究方法有解析法、有限元法和模态数值法。较为典型的研究有:翟婉明院士[9]将轨道板作为支承于连续分布的线性弹簧和线性阻尼上的有限长自由梁,将钢轨作为离散弹性点支承的欧拉梁,运用模态叠加技术,在时域内建立了车辆与板式轨道耦合的动力学数值模型,分析了轨道系统在不平顺激励下的动力特性;XIANG Jun等学者[10]根据弹性系统动力学总势能不变原理及形成系统矩阵的“对号入座”法则,建立了列车—浮置板轨道系统的竖向振动有限元模型,分析了不平顺激励下列车引起浮置板轨道的动力响应;吴川等学者[11]针对短型浮置板轨道,运用傅氏变换的方法,建立相应解析模型对其隔振性能进行分析;李增光等[12]将浮置板考虑为有限长梁,将扣件和隔振器视为离散的弹簧阻尼元件,提出浮置板轨道的动柔度计算方法,并分析了其隔振性能。
然而,现有绝大多数关于浮置板轨道动态特性的力学模型均需要将钢轨与多块分段的轨道板进行耦合计算,致使模型计算的时耗成本巨大。为提高模型计算效率,文献[13]提出将板式轨道作为一种周期性的无限长结构,运用移动谐振荷载作用下周期结构响应的性质,将无限轨道响应问题的求解映射在1块浮置板所对应的轨道结构之内进行,给出了求解浮置板轨道在移动谐振荷载作用下其动力响应的解析解法。在此基础上,文献[14]进一步引入钢轨数学模态,提出了求解移动荷载作用下浮置板轨道动力响应的频域快速数值算法。该算法同样只需在1块浮置板所对应的轨道结构范围内进行钢轨和浮置板的耦合计算,即可求得无限长轨道的动力响应。但文献[13—14]给出的高效算法只适用于移动谐振荷载激励下的情况,不适用固定谐振荷载激励下的情况。鉴于此,本文开展固定谐振荷载激励下浮置板轨道动力响应求解方法的研究。
1 浮置板轨道力学模型
将浮置板轨道视为以轨道板板长为1个周期的周期性无限长轨道结构[13](可称为无限—周期轨道结构),建立图1所示的轨道模型。其中,1块完整轨道板所对应的轨道范围称为特征周期。在模型中,钢轨被模拟为无限长欧拉梁,按扣件间距被离散支承在一系列有限长的浮置轨道板上,而这个有限长的浮置轨道板被模拟为按隔振器间距离散支承在固定基础上的欧拉梁,扣件和隔振器被模拟为弹簧阻尼元件。模型忽略浮置轨道板之间的几何间隙,将坐标原点O取在某相邻2块轨道板的交接处。模型中轨道参数的物理量约定如下:钢轨的抗弯模量为ErIr,线密度为mr;扣件刚度为kr,阻尼为cr,间距为dr;浮置轨道板长为L,抗弯模量为EsIs,线密度为ms;隔振器刚度为ks,阻尼为cs,间距为ds;钢轨和浮置板的位移响应分别为ur和us,且均以竖直向下为正方向。

图1 无限—周期浮置板轨道
2 浮置板轨道动力响应分析的广义波数法
由于固定荷载可视为移动速度为0的特殊移动荷载,因此先从研究速度为v(≠0)的简谐移动荷载F(t)=eiωlt作用下浮置板轨道的动力响应入手。无限—周期浮置板轨道的频域位移响应在空间上呈周期性的特点,满足[12]
(1)
(2)

利用式(1)和式(2),使用文献[14]的“频域快速数值算法”可求解移动谐振荷载引发的轨道结构动力响应。“频域快速数值算法”首先是对图1所示的坐标在x=0到x=L的特征周期范围内浮置板轨道结构的动力响应进行求解,而后再以式(1)和式(2)的周期性关系将该范围的响应进行拓展,以求得无限长轨道的动力响应。但在该算法的求解过程中,荷载移动速度v会始终出现在分母上,无法直接令v=0使移动荷载退化为固定荷载,致使该算法无法用于求解固定谐振荷载作用下轨道的动力响应。
为了解决这个问题,对“频域快速数值算法”进行拓展,引入广义波数β=(ω-ωl)/v,并沿用“频域快速数值算法”的思路,将特征周期x=0到x=L范围内的轨道结构从无限轨道结构中取出并单独进行研究,但对相应的动力控制方程和边界条件方程做广义波数替换,即
动力控制方程:

(3)
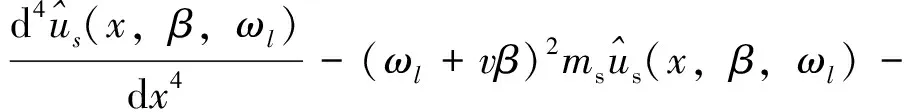
(4)
边界条件:
j=0,1,2,3
(5)
j=2,3
(6)
式中:x0为t=0时刻荷载位置;Nr和Ns分别为特征周期范围内钢轨支点和浮置板支点的个数;xrj及xsj分别为特征周期范围内第j个钢轨支点及板下第j个浮置板支点的坐标;δ()为Dirac函数。
(7)
(8)
将式(8)写成傅里叶级数形式,即
(9)
式中: ei(ξn-β)x为钢轨的数学模态[12];Cn(β,ωl)为对应钢轨数学模态的模态振型坐标,其是包含广义波数及激振频率的未知函数。
实际计算中钢轨数学模态可对称取有限项,即
(10)
式中:2N+1为纳入计算的钢轨数学模态数,将其记为NR。
浮置板位移可用自由欧拉梁的模态叠加表示为
(11)
式中:Xp(x)为自由欧拉梁的第p阶模态振型函数,其计算参见文献[7];Tp(β,ωl)为相应模态的振型坐标;NMS为使得其对应的模态频率大于分析需要的最高频率的模态数。
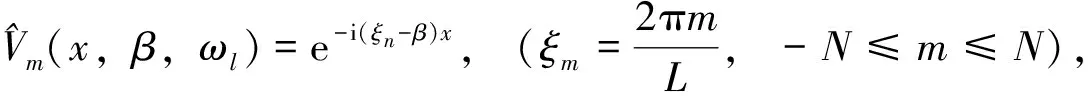
[ErIrL(ξn-β)4-(ωl+vβ)2mrL]Cn(β,ωl)+
(12)

p=1~NMS
(13)
A(β,ωl)c(β,ωl)=P(β,ωl)Leiβx0/v
(14)
其中,c(β,ωl)={C-N(β,ωl),C-N+1(β,ωl),…,CN(β,ωl),T1(β,ωl),…,TNMS(β,ωl)}T
式中:c(β,ωl)为各模态振型坐标组成的向量;A(β,ωl)为(NR+NMS)×(NR+NMS)阶方阵;P(β,ωl)为(NR+NMS)×1阶向量, 且其第j行值如下式。
(15)
式(14)中c(β,ωl)是未知的,A(β,ωl)和P(β,ωl)为已知, 由于P(β,ωl)的取值与β及ωl均无关,下文为了方便将其简写成P。
解式(14)可得
(16)


e-inβLB(β,ωl)c(β,ωl)=
(17)
B(β,ωl)=


A(β,ωl)-1Peivβtdβ]eiωlt
(18)
上式即为谐振荷载以速度v移动时,轨道结构的时域位移响应解。在上式中令v→0,即可得到固定位置谐振荷载(荷载作用点x0)作用下轨道结构的时域位移响应
A(β,ωl)-1Pdβ]eiωlt
(19)
式(19)表明:在固定谐振荷载作用下,浮置板式轨道结构的时域稳态响应也是简谐的,且响应幅值为

(20)
Le-iβ(nL-x0)B(β,ωl)A(β,ωl)-1P。
3 计算分析
运用上节推导的广义波数法,研究固定位置谐振荷载作用下浮置板轨道动力响应随荷载频率的变化特性,即幅频特性。浮置板轨道的计算参数按北京地铁5号线某区段钢弹簧浮置板轨道的参数取值,具体见表1。其中,钢轨和浮置板的损耗因子ηr和ηs是反映材料自身阻尼的参数,在模型计算中仅需用Er(1+i)和Es(1+i)替换Er及Es。计算的分析频率上限取为1 000 Hz。

表1 浮置板轨道参数
注:以上轨道参数均对应于两股钢轨


图2 不同钢轨数学模态阶数下的模
考虑固定谐振荷载F(t)=eiωlt作用于浮置板中部位置对应的钢轨处,研究图4所示轨道纵向荷载激励点A、距激励点L/4(7.5 m)处B、距激励点L/2(15 m)处C、距激励点3L/4(22.5 m)处D以及距激励点L(1个完整板长30 m)处E的动力响应(各个监测点处的钢轨和浮置板响应一并研究)。其中,C在2块轨道板交接处,将交接处的2个板端分别记为C-和C+。

图的模
图5给出了由本文广义波数法计算得到的A—E处钢轨及浮置板的幅频响应曲线。图6给出了钢轨和浮置板A—E处的幅频衰减规律。为了对本文方法进行验证,在图5(a)中同时给出了由动柔度方法[12]计算得到的A处幅频响应曲线。

图4 浮置板轨道所受激励及响应拾振点位置




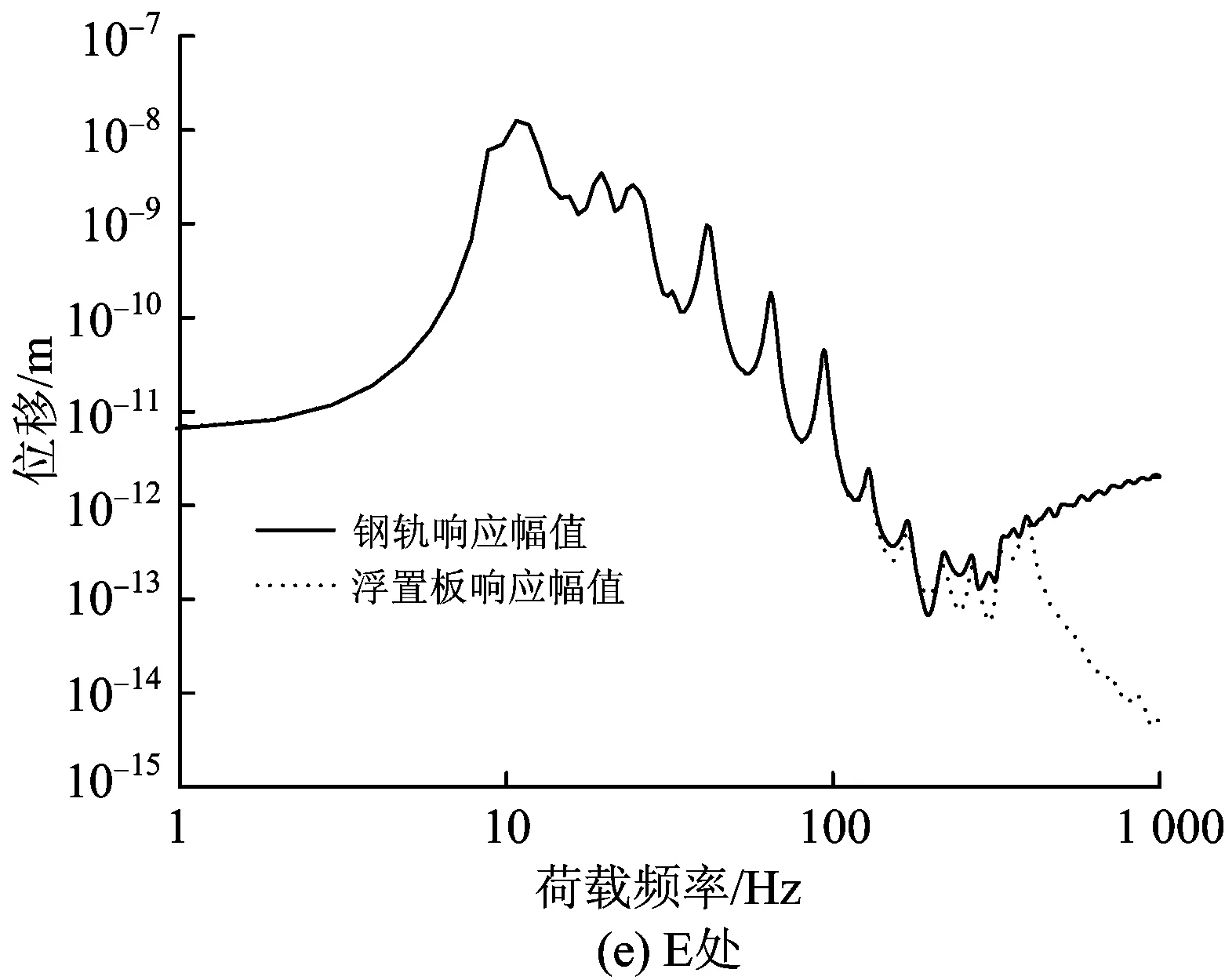
图5 A—E点的幅频特性
从图5(a)中可见:
(1)2种方法计算得到的轨道幅频响应曲线吻合得较好,从而验证了本文方法的正确性。


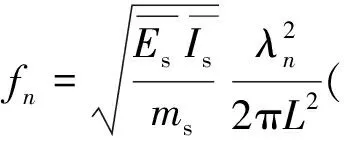

图6 浮置板轨道幅频特性沿轨道纵向的变化
由图5和图6可以看出固定位置激励下轨道不同位置动力特性的变化。
(1)在荷载激励点A处,钢轨和浮置板的振动幅值只在频率小于15 Hz的荷载作用下相差不大,然而在离荷载激励点较远的其他点(B,D,E,板端C除外),钢轨和浮置板在1个更宽频段,小于200 Hz频段(接近由钢轨及扣件所构成的上部体系的固有频率)内的荷载作用下呈现出几乎相同的振幅。
(2)浮置板轨道存在板端效应:在板端C处,钢轨与浮置板在振动上具有比B,D,E等其他非激励点更大的差异,且在某些频段(如20~300 Hz频段)荷载激励下,浮置板在板端C-处的响应甚至会出现大于该点钢轨响应的情况(见图5(c));当振动沿轨道纵向传播时,一些频段(如15~27及45~70 Hz频段)荷载激励引发浮置板在板端C-处的响应也会出现大于离激励点更近点B的情况(见图6(b)),即浮置板在板端处的响应会出现放大现象。
(3)由于浮置板的不连续性,振动从激励所在轨道板对应的轨道范围传递到其他轨道板对应的轨道范围时,将产生明显衰减(见图6)。
(4)频段0~8 Hz及频段40~1 000 Hz内荷载引发的振动沿浮置板轨道纵向衰减明显,而频段8~40 Hz内荷载引发的振动沿轨道纵向的衰减相对缓慢(见图6)。
4 结 论
(1)本文提出了固定谐振荷载作用下浮置板轨道动力响应求解的广义波数方法。该方法将固定荷载视作速度为0的移动荷载,可将无限轨道动力响应问题的求解映射在1个周期范围内进行,具有较高的计算效率。通过与其他模型计算值的比较,验证了该方法的正确性和准确性。
(2)浮置板轨道存在明显的板端效应,即在固定位置激励引发的振动沿轨道纵向传播时,浮置板在板端处的响应往往会出现放大现象,甚至会出现大于该处钢轨响应的情况。
(3)在不同频率荷载引发的振动沿浮置板轨道纵向的衰减上,频段0~8 Hz及频段40~1 000 Hz内荷载引发的振动衰减明显,而频段8~40 Hz内荷载引发的振动衰减相对缓慢。
[1]丁德云,刘维宁,李克飞,等. 钢弹簧浮置板轨道参数研究[J]. 中国铁道科学,2011, 32(1):30-35.
(DING Deyun, LIU Weining, LI Kefei, et al. Parametric Study of the Steel Spring Floating Slab Track[J]. China Railway Science,2011, 32(1):30-35. in Chinese)
[2]LOMBAERT G, DEGRANDE G, Vanhauwere B, et a1. The Control of Ground-Borne Vibration from Railway Traffic by Means of Continuous Floating Slabs[J]. Journal of Sound and Vibration, 2006, 297(3/4/5): 946-961.
[3]CUI F, CHEW C H. The Effectiveness of Floating Slab Track System—PartⅠ. Receptance Methods[J].Applied Acoustics, 2000, 61(4): 441-453.
[4]WILSON G P, SAURENMAN H J, NELSON J T. Control of Ground-Borne Noise and Vibration[J].Journal of Sound and Vibration,1983, 87(2): 339-350.
[5]HUSSEIN M F M, HUNT H E M.Modelling of Floating-Slab Tracks with Continuous Slabs under Oscillating Moving Loads[J].Journal of Sound and Vibration, 2006, 297 (1/2): 37-54.
[6]KUO C M, HUANG C H, CHEN Y Y.Vibration Characteristics of Floating Slab Track[J].Journal of Sound and Vibration,2008, 317(3/4/5):1017-1034.
[7]王澜,宣言,万家,等. 浮置板式轨道结构隔振效果仿真研究[J]. 中国铁道科学, 2005, 26(6): 48-52.
(WANG Lan, XUAN Yan, WAN Jia, et al. The Simulation Research on the Vibration Insulation Performance of the Floating Slab Track Structure[J]. China Railway Science,2005, 26(6): 48-52.in Chinese)
[8]周萌,韦凯,周顺华,等. 轨道型式对地铁与建筑物共建结构振动响应的影响[J]. 中国铁道科学, 2011, 32(2): 33-40.
(ZHOU Meng, WEI Kai, ZHOU Shunhua, et al. Influence of Different Track Types on the Vibration Response of the Jointly-Built Structure of Subway and the Buildings[J]. China Railway Science,2011, 32(2): 33-40.in Chinese)
[9]翟婉明. 车辆—轨道耦合动力学[M].3版. 北京: 科学出版社, 2007.
(ZHAI Wanming. Vehicle-Track Coupling Dynamics[M]. 3rd ed.Beijing: Science Press, 2007. in Chinese)
[10]XIANG J, HE D, ZENG Q Y.Analysis Theory of Spatial Vibration of High-Speed Train and Slab Track System[J].Journal of Central South University of Techno1ogy,2008, 15(1):121-126. in Chinese)
[11]吴川,刘学文,黄醒春. 短型浮置板轨道系统隔振性能研究[J]. 振动与冲击, 2008, 27(8):74-76,101,113.
(WU Chuan, LIU Xuewen, HUANG Xingchun. Study on Effectiveness of Short Floating Slab Track System[J].Journal of Vibration and Shock,2008, 27(8):74-76,101,113. in Chinese)
[12]李增光, 吴天行. 浮置板轨道动柔度计算方法及隔振性能研究[J]. 振动工程学报, 2007, 20(3): 207-212.
(LI Zengguang, WU Tianxing. Study on the Vibration Isolation Performance of Floating Slab Track Using Dynamic Receptance Method[J]. Journal of Vibration Engineering, 2007, 20(3): 207-212. in Chinese)
[13]马龙祥,刘维宁,刘卫丰.移动谐振荷载作用下浮置板轨道的动力响应[J]. 工程力学,2012,29(12):334-341.
(MA Longxiang, LIU Weining, LIU Weifeng. Dynamic Response of Floating Slab Track Due to a Harmonic Moving Load[J]. Engineering Mechanics, 2012,29(12):334-341. in Chinese)
[14]马龙祥,刘维宁,李克飞.移动荷载作用下浮置板轨道振动响应的频域快速数值算法[J]. 铁道学报,2014,36(2):86-94.
(MA Longxiang, LIU Weining, LI Kefei. Fast Numerical Algorithm of Floating Slab Track Vibration Response Under Moving Loads in the Frequency Domain[J]. Journal of the China Railway Society, 2014,36(2):86-94. in Chinese)
