动车组轴箱弹簧多响应稳健优化设计方法

李永华，董少迪

(大连交通大学 交通运输工程学院，辽宁 大连　116028)

目前，车辆轴箱弹簧优化设计的研究主要集中在优化模型和优化算法两方面。

在优化模型方面，孙剑萍等[1]、王红等[2]提出了基于模糊数学和可靠性优化设计理论的优化模型，在保证弹簧轻量化的同时实现了弹簧防共振性、静强度、疲劳强度的优化；商跃进等[3]利用系统工程方法建立了变刚度弹簧组的优化模型，在使弹簧轻量化的同时，分析了对减振装置中楔块形状的影响程度。但上述优化模型极少考虑弹簧的簧条直径、弹簧中径、工作圈数、剪切模量及密度等影响因素发生波动时对弹簧的质量、刚度和自然频率等质量特性的影响。为了使弹簧的质量特性对这些影响因素的变化不敏感，商跃进等[4]又提出了机车轴箱弹簧的稳健优化设计方法，但所建立的优化模型仅考虑了弹簧的单个质量特性对弹簧稳健性设计的影响，未考虑影响因素变化情况下弹簧的刚度、自然频率、质量等多个弹簧质量特性的稳健性。为了保证弹簧的各质量特性对弹簧的簧条直径、弹簧中径、工作圈数、剪切模量及密度等影响因素的波动不敏感，实现弹簧的多个质量特性的稳健性，有必要对动车组轴箱弹簧进行多响应稳健优化方法的研究。

在优化算法方面，韩锟等[5-6]提出1种遗传算法与蚁群算法结合的混合算法，使其能快速、准确实现全局优化解，但遗传算法易陷入局部最优，蚁群算法又有收敛速度慢的缺点。

为避免这些缺点，学者们提出了可以解决全局最优、高效准确的优化算法和多响应稳健优化方法[7-11]，如改进的广义距离函数法[7]、满意度函数法[8]、新的D-optimal试验设计方法[9]、均方误差法[10]等，以及Yadav等[11]提出如何权衡多个具有相关性的质量特性，对多个具有相互冲突的质量特性进行了优化研究。这些研究主要关注多响应稳健优化的理论及方法，但未进行实际应用研究。并且在优化时无法准确把握设计者的偏好。物理规划法具有灵活度高、计算简便、把握实际等优点，能有效地处理多目标问题，可准确地把握设计者的偏好，有效地权衡各质量特性的稳健性，从实际出发解决动车组轴箱弹簧多响应特性的稳健性问题。

本文在考虑动车组轴箱弹簧的簧条直径、弹簧中径、工作圈数等可控因素及剪切模量、密度等不可控因素及其相互关系的基础上，根据物理规划法的偏好函数权衡动车组轴箱弹簧各质量特性(质量、刚度、自然频率)的稳健性，把握设计者的满意度，构建多响应稳健优化模型，从而获得稳健优化解，并与传统解进行对比分析。

1　动车组轴箱弹簧多响应稳健优化模型

稳健性要求产品的质量特性值对影响因素的干扰不敏感[12]。在设计弹簧中考虑的影响因素主要有簧条直径、弹簧中径、工作圈数、剪切模量及密度等，这些影响因素会造成弹簧质量、刚度和自然频率等质量特性的波动。信噪比是衡量弹簧稳健性的评价指标，其值越大则表示弹簧质量波动越小，即质量特性偏离目标值的程度越小，弹簧越具有较高的稳健性。本文采用信噪比的方法[13]度量弹簧的多质量特性对影响因素变化的波动，通过计算各质量特性的信噪比值，并拟合成信噪比函数，使其达到最大化，以保证多响应质量特性的稳健性。另外，由于不同设计师对于轴箱弹簧的设计变量选取有不同的偏好，这会影响弹簧的多响应质量特性。因此，本文利用物理规划法[14]的偏好函数对各质量特性进行满意度划分，从实际出发，高效、简便地权衡弹簧中的各质量特性，以解决同时实现多个质量特性稳健性的问题。

1.1　质量特性值的信噪比

常用的信噪比主要有3种类型[13]，分别如下。

(1)具有望目特性质量特性的信噪比SN1。当动车组轴箱弹簧的质量特性值y有1个确定不为零的目标值，则

(1)

(2)具有望小特性质量特性的信噪比SN2。当动车组轴箱弹簧的质量特性值y不取负值，且越小越好，目标值为零，则

(2)

式中：yq为弹簧在第q次试验的质量特性值。

(3)具有望大特性质量特性的信噪比SN3。当动车组轴箱弹簧的质量特性值y不取负值，且越大越好，目标值为零时最差，则

(3)

1.2　物理规划法

物理规划法是一种处理多目标优化设计的有效方法，主要应用偏好函数反映设计者的满意度[15]。偏好函数是一种为实现设计者要求的定量定性的描述，一般可分极小型、极大型、趋于某范围型、趋于某目标型4种类型，每种类型又由“软”型和“硬”型2种情况组成[16]。为实现动车组轴箱弹簧中各质量特性的稳健性，一般要求其质量特性的信噪比值越大越好，故采用极大型软偏好函数描述，该函数将其5个分曲线段分别进行拟合[17]，如图1所示。图中：i为设计目标的个数，i=1,2,…,t；yi为第i个设计目标的质量特性值；yik为第i个设计目标的质量特性值在第k段的区间边界值，k=1，2，…，5；fk为第k段的区间边界偏好值；fik为第i个设计目标质量特性值在第k段的区间偏好函数。

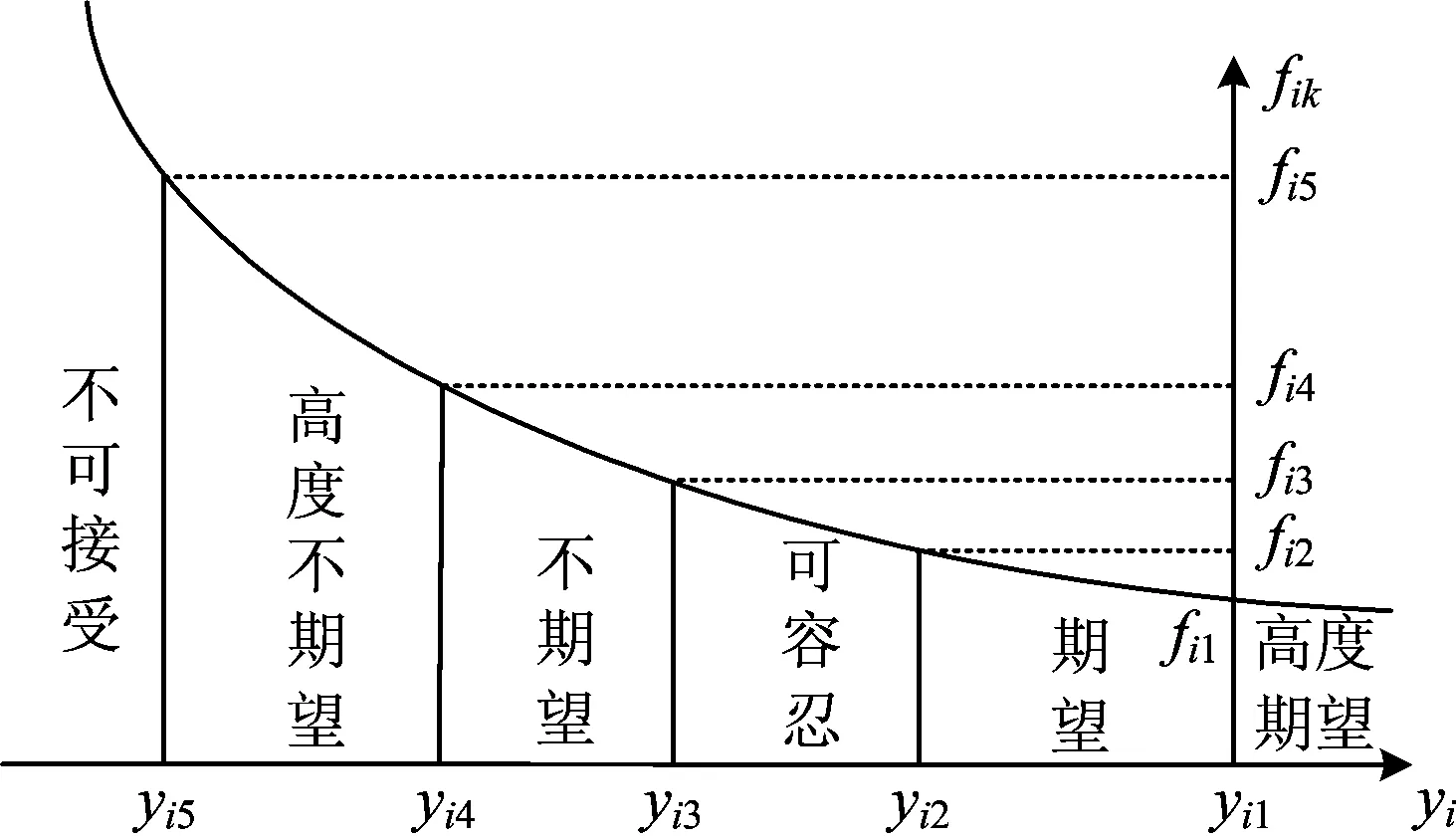
图1　极大型软偏好函数

极大型软偏好函数的拟合曲线表达式为

(4)

c(yi(k-1)-yi)+dk=2，3，…，5

(5)

其中，

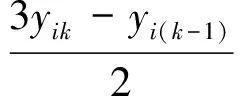
综合所有设计目标的偏好函数，得出总偏好函数fv为

(6)

其中，

X=(x1,x2,x3)

式中：X为动车组轴箱弹簧设计变量的向量，其中x1为簧条直径，x2为弹簧中径，x3为工作圈数；fik[yi(X)]为包含动车组轴箱弹簧设计变量X的第i个设计目标质量特性在第k段的偏好函数。

1.3　多响应稳健优化模型建立

结合信噪比与物理规划法得出动车组轴箱弹簧各质量特性信噪比函数的总偏好函数，并将其作为目标函数，给出相应的约束条件，构建基于物理规划法的动车组轴箱弹簧多响应稳健优化模型。

(7)

s.t.

ySNH-i(X)≥ySNH-iL(X)

gj(X)≤0

XL≤X≤XU

式中：H代表信噪比的望目特性、望小特性和望大特性，H=1,2,3；fik[ySNH-i(X)]为第i个设计目标的质量特性的信噪比函数ySNH-i(X)在第k段的偏好函数；ySNH-iL(X)为第i个设计目标的质量特性的信噪比函数的最小值；gj(X)为轴箱弹簧的不等式约束，j为约束条件的个数，j=1,2,…,l；XU和XL分别为设计变量X的上、下界。

2　动车组轴箱弹簧多响应稳健优化流程

动车组轴箱弹簧多响应稳健优化流程如图2所示。

动车组轴箱弹簧多响应稳健优化的主要步骤如下。

步骤1：分析影响因素。确定影响动车组轴箱弹簧稳健性的影响因素，并按可控影响因素与不可控影响因素分类；再根据弹簧的设计要求确定其水平值。

步骤2：确定弹簧的质量特性。在动车组轴箱弹簧多响应稳健优化设计中，以自然频率、刚度和质量等为质量特性，进一步分析各质量特性的信噪比特性并选择相应的信噪比函数。

图2　多响应稳健优化流程图

步骤3：建立多响应稳健优化模型。首先确定动车组轴箱弹簧的设计变量，并采用正交试验设计方法列出正交表，计算得出动车组轴箱弹簧的各质量特性值及相应的信噪比值；然后根据物理规划法构建信噪比的偏好函数，以及基于动车组轴箱弹簧各质量特性的信噪比值拟合得到其多响应质量特性的信噪比函数，再根据设计者的偏好构建各偏好函数；若某些偏好函数不能满足设计的要求，则需要重新根据物理规划法的偏好结构建立偏好函数，若满足设计要求，则对各偏好函数进行整合，构建总偏好函数，并以此作为设计目标；最后以轴箱弹簧自身参数为边界条件，以强度、静挠度等为约束条件，构建动车组轴箱弹簧的多响应稳健优化模型。

步骤4：求解优化模型。运用ISIGHT平台中的拉丁超立方试验设计抽样方法进行采点抽样，结合多岛遗传算法对模型进行组合优化求解，高效、准确、快速地找出优化模型的全局稳健性最优解。

3　实例分析

某型动车组中的某辆动车[18]，其定员为100人，定员质量为56 t，其轴箱弹簧装置的具体参数见表1。

3.1　分析影响因素

在对动车组轴箱弹簧进行优化设计时，选取簧条直径x1、弹簧中径x2、工作圈数x3为可控因素，选取轴箱弹簧的剪切模量z1和密度z2为不可控因素，其具体参数的水平值见表2。

表1　某型动车组轴箱弹簧装置参数表

表2　轴箱弹簧的影响因素及其参数的水平值

3.2　确定质量特性

在动车组轴箱弹簧多响应稳健优化设计中，以自然频率、刚度和质量为多响应质量特性，计算其质量特性值。

自然频率在一定范围内具有望大特性，其质量特性值y1为

(8)

刚度具有望目特性，其质量特性值y2为

(9)

质量具有望小特性，其质量特性值y3为

(10)

因此，计算动车组轴箱弹簧自然频率、刚度和质量的信噪比时应分别采用式(3)、式(1)和式(2)。

3.3　建立多响应稳健优化模型

正交试验设计中需考虑3个设计变量(可控因素)与假设的交互作用，故可采用正交表L18(21×37)，同时试验还受到2个三水平噪声因子(不可控因素)的影响，每个试验组合需执行3次，则计算轴箱弹簧的内、外簧的质量特性值共进行108次试验。根据轴箱弹簧各质量特性的要求，按信噪比公式可计算出各质量特性值的信噪比值，见表3。

根据表3数据，应用MATLAB软件中的最小二乘法，可拟合出动车组轴箱弹簧内簧的各质量特性信噪比函数为

(11)

(12)

(13)

同理，拟合得出动车组轴箱弹簧外簧的各质量特性信噪比函数为

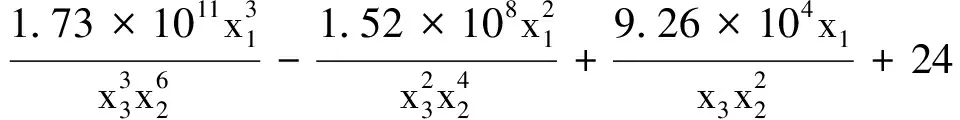
(14)

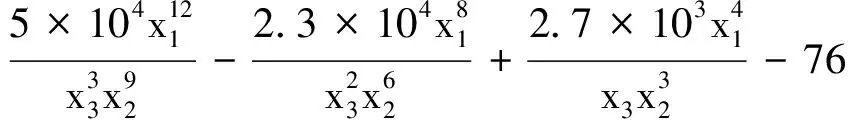
(15)

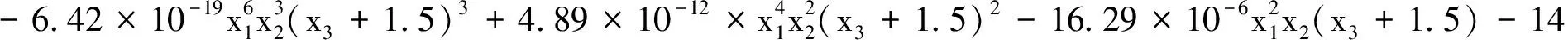
(16)

表3　内、外簧的质量特性值及信噪比值

将上述得出的各信噪比函数作为新的响应，根据各自的偏好函数，得出信噪比函数的总偏好，结合动车组轴箱弹簧的性能约束与边界约束，利用文中所提方法构建动车组轴箱弹簧的多响应稳健优化模型为

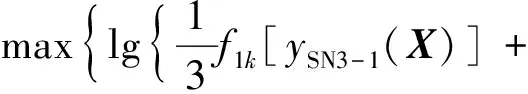
(17)

s.t.

ySN3-1(X)≥38.01(内簧)，

ySN3-1(X)≥38.13(外簧)

ySN1-2(X)≥4.94(内簧)，

ySN1-2(X)≥3.96(外簧)

ySN2-3(X)≥-23.18(内簧)，

ySN2-3(X)≥-31.95(外簧)

g2=3.5x2≥h0

mL≤m≤mU

x1L≤x1≤x1U

x2L≤x2≤x2U

x3L≤x3≤x3U

其中，

Pmax=Pv(1+Kvd)

h0=(x3+1)x1+fmax

式中：fmax为弹簧最大静挠度，mm；Pv为作用在弹簧上的垂向静载荷，kN；Pmax为作用在弹簧上的最大垂向载荷，kN；Kvd为弹簧动载荷系数；C为弹簧曲度系数；h0为弹簧自由高度，mm；τ-1为剪切许用应力，MPa；m为弹簧的旋绕比；mU和mL分别为旋绕比m的上限和下限，分别取7和4；x1U和x1L分别为簧条直径x1的上限和下限，内簧分别取31和21 mm，外簧分别取46和36 mm；x2U和x2L分别为弹簧中径x2的上限和下限，内簧分别取153和133 mm，外簧分别取230和210 mm；x3U和x3L为工作圈数x3的上限和下限，内簧分别取4.9圈和3.9圈，外簧分别取3.4圈和2.4圈。

3.4　稳健优化模型求解及结果分析

运用ISIGHT软件中拉丁超立方试验设计抽样方法进行采点抽样，结合多岛遗传算法对式(17)进行组合优化[19]求解，并将其优化解(简称稳健优化解)与传统优化解进行对比，计算结果见表4。图3为动车组轴箱弹簧各质量特性稳健性优化前后的概率密度曲线。

从表4可知：得到的稳健优化组合并不是正交试验设计中的水平组合，而是通过物理规划法得到的具有极大信噪比值的水平组合，并且优化后的自然频率和弹簧刚度的信噪比值在设计者偏好函数的期望区间内，优化后的重量则在设计者可容忍的区间内。

从图3可知：得到的稳健优化解减少了质量特性的方差波动，从而降低了不可控因素的干扰，使轴箱弹簧的自然频率、刚度、质量等质量特性具有稳健性。

表4　稳健优化解与传统优化解的对比

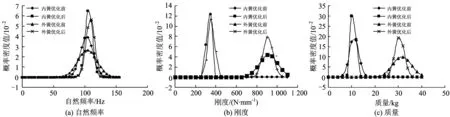
图3　内、外簧各质量特性稳健优化前后的概率密度曲线图

4　结　语

(1)在考虑可控因素与不可控因素的相互关系的基础上，提出1种基于信噪比和物理规划法的多响应稳健优化方法。其中，信噪比指标可评价稳健性，物理规划法可高效地处理多个响应优化问题，结合信噪比与物理规划法能够有效解决多响应稳健性优化问题，从而构建出轴箱弹簧的多响应稳健性优化模型。

(2)为高效、快速地获得高精度的全局最优解，本文充分利用组合优化算法拉丁超立方抽象的全局性和多岛遗传算法高效准确的特点，对轴箱弹簧的多响应稳健优化模型进行求解，所得到的全局稳健性最优解，不仅满足了设计者的要求，而且提高了使其信噪比值，减小了各质量特性值的方差波动范围，进而降低了弹簧各质量特性对影响因素的敏感性，从而实现了动车组轴箱弹簧多个质量特性的稳健性。

(3)对动车组轴箱弹簧的优化实例研究表明，该方法在优化动车组轴箱弹簧各质量特性的同时，实现了其各质量特性的稳健性，保证了动车组运行的平顺性与安全性，与传统优化方法的对比也验证了本文方法的有效性，并可进一步推广到动车组其他复杂零部件的多响应稳健优化设计中。

[1]孙剑萍, 罗意平. 基于模糊熵的柴油机气门弹簧的可靠性优化设计[J]. 机械设计, 2014, 31(6):37-42.

(SUN Jianping, LUO Yiping. Reliability Optimization Design Based on Fuzzy Entropy about Valve Springs of Diesel Engine [J]. Journal of Machine Design, 2014, 31(6): 37-42. in Chinese)

[2]王红, 汤劲松, 刘万选. 基于模糊理论的车辆变刚度弹簧组可靠性优化设计[J]. 西南交通大学学报，2014, 49(5): 837-841.

(WANG Hong, TANG Jinsong, LIU Wanxuan. Reliability Optimization Design of Vehicle Variable Stiffness Spring Assembly by Fuzzy Theory [J]. Journal of Southwest Jiaotong University, 2014,49(5):837-841. in Chinese)

[3]商跃进, 王红. 变刚度弹簧组系统优化设计[J]. 铁道学报, 2006, 28(6): 51-54.

(SHANG Yuejin, WANG Hong. Optimized Design of Variable-Stiffness Spring Combinations System[J]. Journal of the China Railway Society, 2006, 28(6): 51-54. in Chinese)

[4]商跃进. 轨道车辆零部件稳健性优化设计[J]. 内燃机车, 2011(8): 19-21，45.

(SHANG Yuejin. Robustness Optimization Design of Components for Railway Vehicle[J]. Diesel Locomotive, 2011(8): 19-21，45. in Chinese)

[5]韩锟, 潘迪夫. 基于混合算法的机车二系弹簧载荷调整优化方法[J]. 中国铁道科学, 2006, 27(2):88-92.

(HAN Kun, PAN Difu. Optimization Model for Adjustment of Locomotive Secondary Spring Load Based on Hybrid Algorithm[J]. China Railway Science, 2006, 27(2):88-92. in Chinese)

[6]潘迪夫, 黎航, 韩锟. 基于遗传算法的机车二系支承载荷调整优化方法[J]. 中国铁道科学, 2005, 26(3): 83-87.

(PAN Difu, LI Hang, HAN Kun. Optimization Model of Locomotive Secondary Spring Load Adjustment Based on Genetic Algorithm[J]. China Railway Science, 2005, 26(3): 83-87. in Chinese)

[7]HE Z, ZHU P F, PARK S H. A Robust Desirability Function Method for Multi-Response Surface Optimization Considering Model Uncertainty[J]. European Journal of Operational Research, 2012, 221(1): 241-247.

[8]何桢, 王晶, 李湧范. 基于改进的距离函数法的多响应稳健参数设计[J]. 天津大学学报, 2010, 43(7): 644-648.

(HE Zhen, WANG Jing, LI Yongfan. An Improved Generalized Distance Function Approach to Multi-Response Robust Parameter Design [J]. Journal of Tianjin University, 2010, 43(7): 644-648. in Chinese)

[9]KOVACH J, CHO B R. A D-Optimal Design Approach to Constrained Multi Response Robust Design with Prioritized Mean and Variance Considerations[J]. Computers & Industrial Engineering, 2009, 57(1): 237-245.

[10]KÖKSOY O. A Nonlinear Programming Solution to Robust Multi-Response Quality Problem[J]. Applied Mathematics and Computation, 2008, 196(2): 603-612.

[11]YADAV O P, THAMBIDORAI G, NEPAL B, et al. A Robust Framework for Multi-Response Surface Optimization Methodology[J]. Quality and Reliability Engineering International, 2014, 30(2): 301-311.

[12]YUE R X. Model-Robust Designs in Multi Response Situations[J]. Statistics & Probability Letters, 2002, 58(4): 369-379.

[13]SHARMA NARESH K, CUDNEY ELIZABETH A. Signal-to-Noise Ratio for Operating Window Using Unified Methodology[J]. Concurrent Engineering Research and Applications, 2009, 17(3), 173-181.

[14]李永华, 宋彦明. 基于物理规划的起重机主梁稳健优化设计[J]. 机械设计与研究, 2006, 22(5): 78-81.

(LI Yonghua, SONG Yanming. Robust Optimization of the Main Girder in Crane Based on Physical Programming[J]. Machine Design and Research, 2006, 22(5): 78-81. in Chinese)

[15]REYNOSO-MEZA G, SANCHIS J, BLASCO X, et al. Physical Programming for Preference Driven Evolutionary Multi-Objective Optimization[J]. Applied Soft Computing, 2014，24: 341-362.

[16]MESSAC A, ISMAIL-YAHAYA A. Multi-Objective Robust Design Using Physical Programming[J]. Structural and Multidisciplinary Optimization, 2002, 23(5): 357-371.

[17]刘莉, 邢超, 龙腾. 基于物理规划的弹道多目标优化[J]. 北京理工大学学报, 2013, 33(4): 357-362.

(LIU Li, XING Chao, LONG Teng. Study of Multi-Objective Trajectory Optimization Based on Physical Programming[J]. Transactions of Beijing Institute of Technology, 2013, 33(4): 357-362. in Chinese)

[18]宁晓丹, 孙保卫, 商跃进，等. CRH2动车组轴箱弹簧疲劳试验方案研究[J]. 长江大学学报：自然科学版, 2008, 5(3): 258-259.

(NING Xiaodan, SUN Baowei, SHANG Yuejin, et al. Research on the Fatigue Test Project of Axle Box Springs Used for CRH2Multiple Units[J]. Journal of Yangtze University：Natural Science Edition, 2008, 5(3): 258-259. in Chinese)

[19]薛红军, 李云锋. 结构优化设计的组合优化策略[J]. 机械强度, 2013, 35(3): 278-282.

(XUE Hongjun, LI Yunfeng. Integrated Optimization Strategy in Structure Optimization Design[J]. Journal of Mechanical Strength, 2013, 35(3): 278-282. in Chinese)