基于改进粒子群算法的牵引供电系统多目标优化设计
2016-03-30陈民武许臣友黄文勋孙小凯
陈民武,许臣友,黄文勋,邱 璐,孙小凯
(1.西南交通大学 电气工程学院,四川 成都 610031;2.中铁第一勘察设计院集团有限公司,陕西 西安 710043)
传统的牵引供电系统设计过于依赖设计人员的专业经验,主要供电设施数量和位置的确定易受主观因素影响,并且由于有限方案的比选也缺乏全局寻优能力,难以保证设计容量的最优[1]。近年来,国内多个铁路设计部门先后引进了国际公认的牵引供电系统设计软件,例如德国SIGNON公司的ELBAS/WEBANET和IFB公司的OpenPowerNet软件,利用牵引负荷过程仿真手段,动态计算系统内潮流分布,计算精度和效率均优于之前广泛采用的平均运量法和概率统计法。但上述商业软件的核心算法不公开,且仅能对给定的设计方案进行计算和分析,同样不具备方案自动寻优能力。
随着国内外高速和重载铁路的快速发展,针对牵引供电系统建模和仿真的研究也较多[2-5]。但这些研究均未涉及实际供电系统的优化问题。文献[6]在已知全线牵引能耗分布的前提下提出了供电系统优化设计的基本思路,针对给定优化目标推导了严格的解析表达式;但实际线路的供电节点多,加之模型的复杂性给求最优解带来了一定困难。群智能算法的研究为解决复杂寻优问题提供了有效途径,并已经在电力系统的无功优化、负荷预测和经济运行等领域取得了成功应用[7-8]。因此,解决实际工程问题的寻优方法可以建立在相关数学模型和群智能算法的基础上,充分利用计算机强大的计算能力,使得结果不断地沿着改善方案自动进行,最终收敛于最优方案,其分析比较的范围也是人工选优不可比拟的。
本文将群智能算法和车—网耦合系统交互仿真相结合,开展牵引供电系统多目标优化设计研究,并结合实际工程算例验证优化模型和算法的正确性及有效性。
1 基于车—网耦合系统交互仿真的牵引供电系统多目标优化模型
1.1 车—网耦合系统模型以及潮流分布计算算法
基于多导体传输线理论构建适用于各种牵引供电方式的牵引网分布参数等效模型,将在线列车、牵引变电所(AT供电方式下含AT所和分区所)以及其他与牵引网横向连接的电气设备等效为分割切面模型。利用牵引变电所三相—两相电气量通用变换关系,构建牵引变电所数学模型[1]。当前高速和重载铁路推广采用自耦变压器(AT)供电方式,该供电方式下供电臂链式车—网耦合系统模型如图1所示。

图1 AT供电方式下车—网耦合系统供电臂链式网络模型
结合AT供电方式下车—网耦合系统供电臂链式网络模型,可以得到统一的节点导纳矩阵Y[2-3]。与电力系统其他电气设备的负荷特性不同,电力机车(含动车组)是时间—空间移动负荷,随着它在不同时刻的分布位置不同,牵引供电系统的拓扑结构也会发生变化,上述系统的链式网络结构和导纳矩阵也是时变的。在设计阶段,根据运行组织计划安排,可以得到任意仿真时间步长T对应全线列车位置。结合线路条件和机车特性,通过牵引计算得到电力机车在当前位置的取用功率,假设有功功率为P,无功功率为Q,则机车初始电流I(0)为
(1)
式中:U(0)为列车对应切面上接触网与钢轨之间的初始电压;j为虚数单位;*表示求复数的共轭。
在建立车—网耦合系统仿真模型的基础上,对应已知牵引供电系统设施数目和位置,通过交互迭代计算,可以求解牵引负荷过程的潮流分布,从而得到第i个牵引变电所的计算容量Si和全线牵引变电所计算容量之和,即全线总容量Ssub。负荷潮流分布计算时的迭代算法流程如图2所示。
按照图2所示的迭代算法流程,前期研究已经完成了上述牵引计算和供电计算仿真平台,并在国内多条高速铁路和重载铁路牵引供电系统设计中加以应用,与ELBAS/WEBANET软件对比,计算结果基本一致,达到了工程设计要求[3,9]。
1.2 牵引供电系统多目标优化模型
AT供电方式下牵引变电所普遍采用2台中抽式单相变压器构造Vx接线[10]。假设某电气化复线区段牵引供电系统初始设计方案中包含NTS个牵引变电所,以全线总容量Ssub和平均有功功率损耗Ploss均最小为优化目标,以牵引变电所、AT所和分区所的数量NTS,NAT,NSP及其位置LTS,LAT,LSP为优化变量(其中LTS,LAT,LSP分别为长度是NTS,NAT,NSP的一维数组),通过调整上述变量的取值,反复进行负荷潮流分布计算,进而得到各个牵引变电所馈线电流的大小,最终决定各个牵引变电所输出的功率以及整个系统的功率损失。
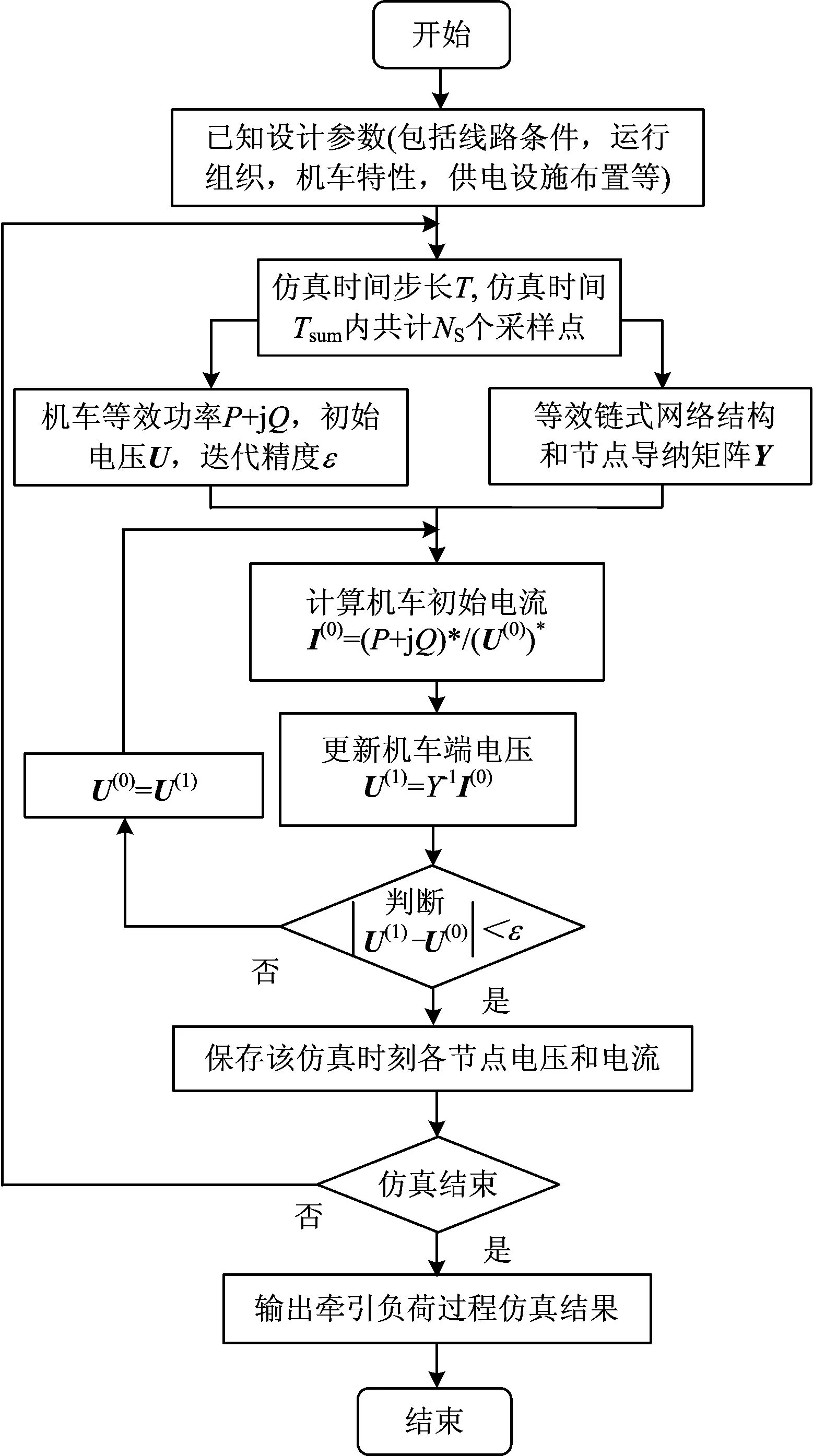
图2 迭代算法流程图
以牵引供电系统主要设计原则为约束条件,以Ssub和Ploss最小为优化目标[11],则牵引供电系统的多目标优化模型可以表示为
(2)
f2=minPloss
(3)
s.t.
ULmin≤ULk≤ULmax
NTS,NAT,NSP≠0
LTS∈A
LAT∈B
LSP∈C
式中:NS为采样点数;Pih为仿真时刻h下牵引变电所i输出的有功功率;K为在线列车数目;PLkh为仿真时刻h下电力机车k的有功功率;Tsum为仿真时间;ULk为电力机车k端的接触网对地电压;A,B和C分别为牵引变电所、AT所和分区所所址位置的可选值域,且根据实际设计需要,还可以补充其他约束条件;ULmin和ULmax分别为机车牵引特性对ULk的限值要求。
在车—网耦合系统模型中,调整优化变量NTS,NAT,NSP和LTS,LAT,LSP的取值,在改变牵引供电设施布置和供电臂长度的同时,也改变了牵引供电系统负荷潮流分布和机车位置的接触网对地电压ULk。在优化过程中如果ULk超出了上述限值要求,则将对应的牵引供电系统设计方案排除。
2 基于Pareto熵的混沌多目标粒子群优化算法
2.1 多目标粒子群优化算法
在1.2节优化模型中,D维优化变量x=(NTS,NAT,NSP,LTS,LAT,LSP)T,其中维数D=NTS+NAT+NSP+3,目标向量F=(f1,f2)T=(minSsub, minPloss)T。将上述最小多目标优化问题描述为
F(x)=(f1(x),f2(x))T
(4)
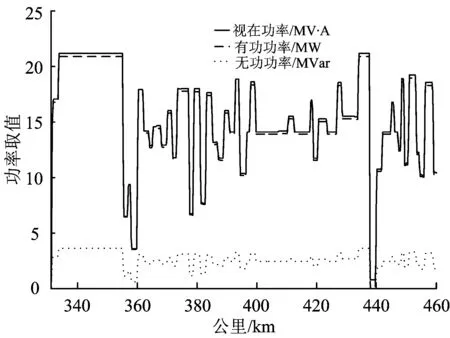
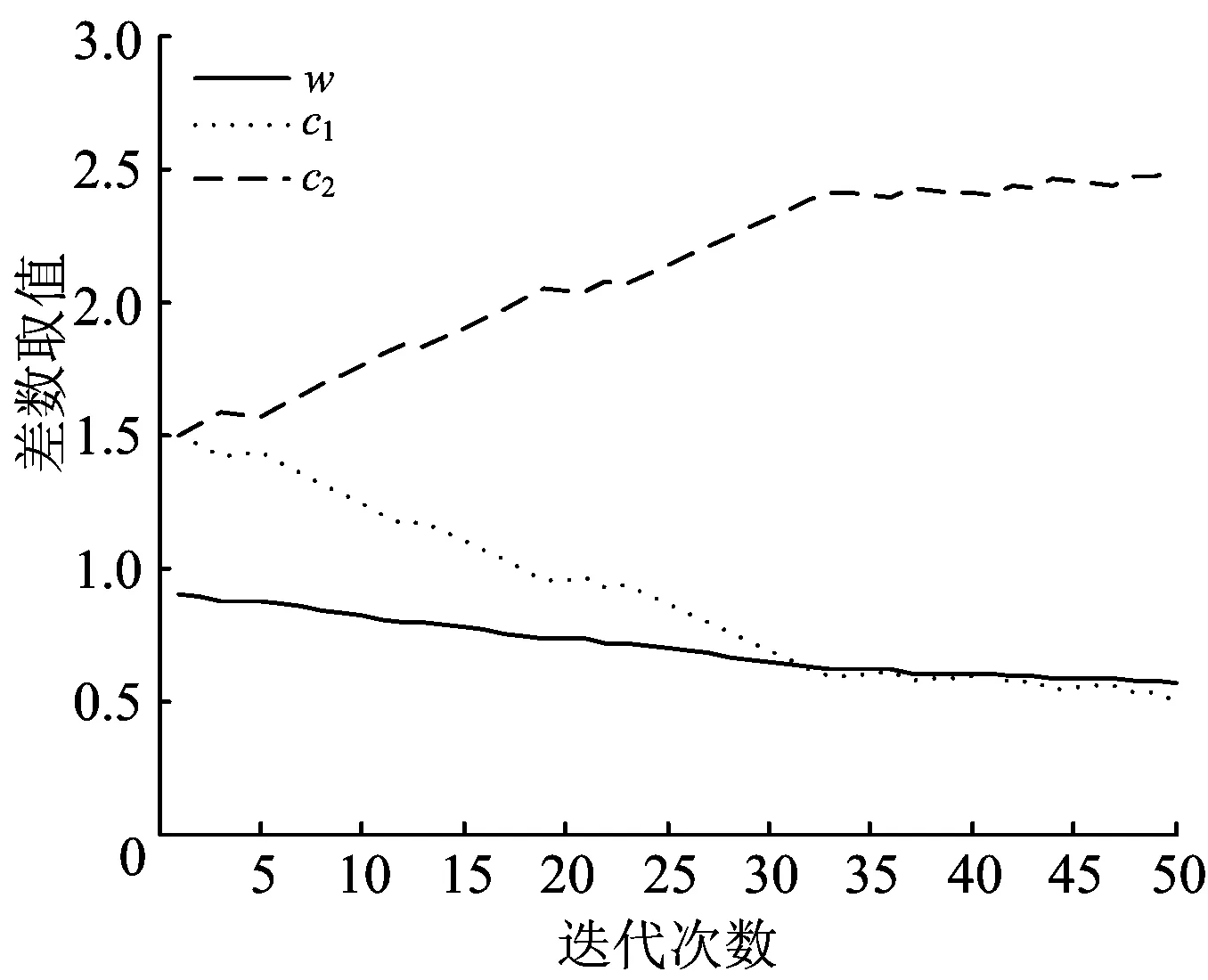
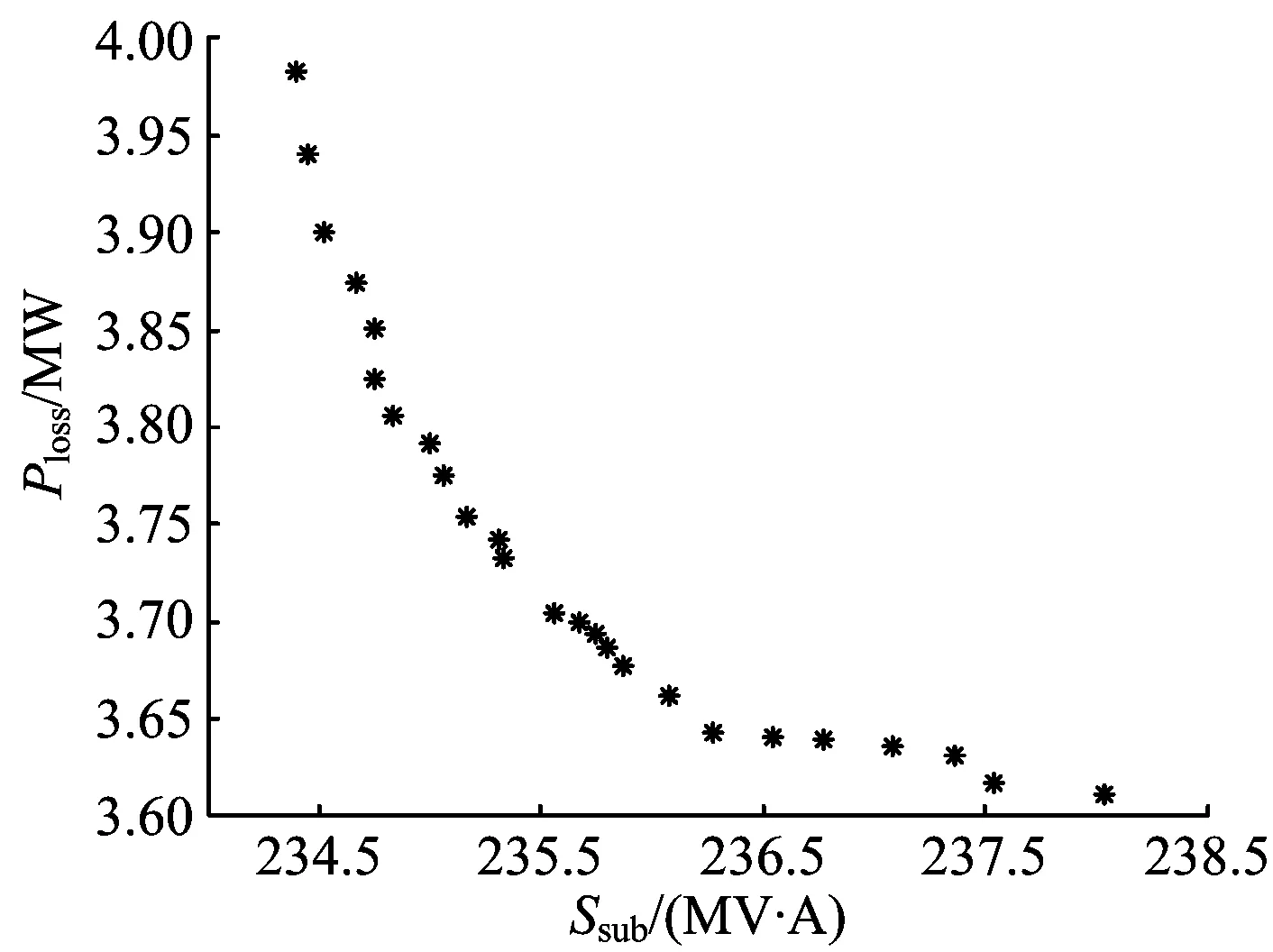
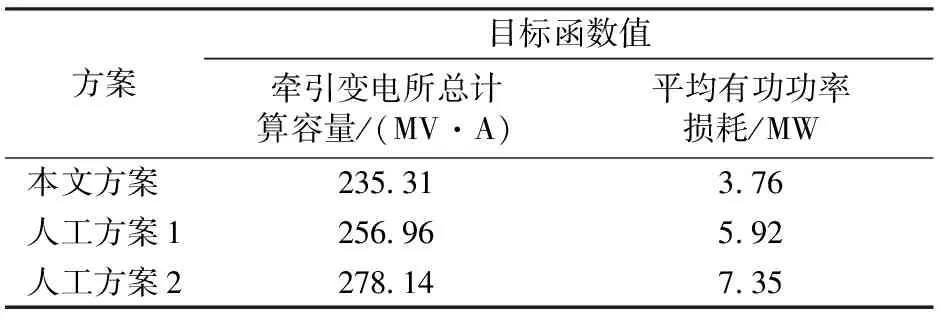
多目标优化问题中的各个目标往往是相互对抗的,大多数情况下各个目标同时达到最优值的可能性比较小,只能是这些目标函数之间的折中解,这就需要引入Pareto占优的概念。设优化变量集合中任意2个D维优化变量x1和x2,当满足l=1,2,fl(x1) (5) 式中:t为迭代次数;w为惯性权重系数,w≥0;b1和b2为在[0,1]上均匀分布的随机数;pBestz表示第z个粒子在第t次迭代时的个体最优位置;c1,c2为学习因子(或称加速因子)。 2.2.1Pareto熵及进化状态检测 熵是微观状态均匀性和多样性的一种度量,表示系统的无序程度。储存在外部档案中的Pareto解的分布均匀性可以由Pareto熵来反映,Pareto熵间接地表征了Pareto前沿解的多样性状态,前后2次迭代熵的变化(差熵)反映了Pareto前沿重新分布的情况,从而通过差熵可以推断种群的进化状态,如收敛状态、多样化状态和停滞状态,通过状态反馈信息动态的调整进化策略,平衡种群的开采和开发能力。Pareto熵的求解见文献[14]。 定义相邻2次迭代的差熵为 ΔE(t)=E(t)-E(t-1) (6) 式中:E为Pareto解的熵;ΔE为差熵。 2.2.2引入个性化混沌因子的自适应进化策略 粒子群优化算法可以通过进化状态反馈信息,动态调整惯性权重系数w和学习因子c1,c2以平衡算法的全局和局部搜索能力。利用混沌序列的遍历性提出自适应调整进化策略。 首先,对每个粒子引入个性化混沌因子γ(t)=μ(z)γ(t-1)(1-γ(t-1)),γ(0)∈rand(0,1),μ(z)∈rand(3.75, 4],通过混沌序列可以提高算法的个性化遍历能力[15]。利用种群收敛状态和差熵对其所有运动参数进行混沌扰动,建立如下调整关系。 1)个性化混沌局部学习因子 c1(t)= (7) 2)个性化混沌全局学习因子 c2(t)= (8) 3)个性化混沌惯性系数 w(t)= (9) 式中:Stepw,Stepc1和Stepc2分别为w,c1和c2的调节步长,分别等于对应参数区间长度除以最大迭代次数。所有参数限制在预先确定的区间内,若超出边界,则取边界值。 2.2.3自适应变异操作 (10) 变异概率计算公式为 (11) 式中:Tmax为最大迭代次数。 可见,当Pareto熵E(t)减小(即群多样性下降)时变异概率ρm增大,需要扩大搜索空间,以避免陷入局部极值。 将基于Pareto熵的混沌多目标粒子群优化算法与牵引供电系统优化模型相结合,确定优化变量为全线牵引变电所、分区所和AT所的数目和位置,进而由潮流计算得到对应的供电容量需求。首先,在优化变量可行域范围内初始化,生成1个粒子群,粒子初始速度是在速度范围内的1组随机数。然后,代入车—网耦合系统交互仿真平台,计算潮流分布和优化目标函数值。在迭代计算过程中,采用近似Pareto分布熵及差熵评估种群的进化状态,并以此作为反馈信息,动态跟踪和调节进化策略和变异算子,利用混沌扰动对变量进行调整。通过协调多个目标函数之间的关系,计算满足约束条件的Pareto解集。具体优化过程如图3所示。 图3 牵引供电系统优化流程图 为了进一步确定最优方案,应用模糊隶属度函数评价每个Pareto解中各个目标函数对应的隶属度,定义模糊隶属度函数如式(12)所示。 (12) 对于Pareto解集中每个解,应用式(13)求其对应的满意度值,将满意度值最大的解所对应的设计方案记为最优方案。 (13) 式中:Ψd为第d个Pareto解的满意度值;G为外部档案最大容量。 以某高速铁路牵引供电系统的优化设计为例,主要设计原则和技术条件如下:①外部电源电压等级220 kV;②复线区段,公里标DK 331.2—DK460.6,全长129.4 km;③供电臂采用全并联供电方式设计,在供电臂末端分区所、供电臂中部AT所实现并联;④牵引变压器采用Vx接线方式;⑤重联机车类型为CRH3型动车组;⑥牵引网持续最高电压为27.5 kV、短时最高电压为29 kV、最低电压正常供电时不低于20 kV;⑦运行组织近期按照4 min追踪运行。根据线路条件和机车运行特性,得到单车牵引负荷曲线计算结果如图4所示。 图4 单车牵引负荷曲线 此外,以牵引变电所、AT所和分区所的位置作为多目标粒子群优化算法中的优化变量,全线牵引变电所、分区所和AT所的选址受多种实际因素影响。为了避免设计方案无法实施,比如受线路平纵面、外部电源方案或者设备运输及生活便利等条件限制,某些位置不能或者不宜作为所址等,可以通过修改优化模型中所址值域A,B和C,在全局寻优过程中自动避开。 结合本文算例,基于Pareto熵的混沌多目标粒子群优化算法主要参数取值如下:最大迭代次数Tmax=50,种群规模N=20,外部档案最大容量G=25,学习因子c1max=c2max=2.5,c1min=c2min=0.5,学习因子c1和c2的初值均取1.5,wmax=0.9,wmin=0.4,惯性权重系数w初值取0.9。在迭代过程中,基于Pareto熵的混沌自适应参数调整策略如图5所示。由图5可见,在迭代初期取相对较大的w,c1和相对较小的c2,使得粒子较均匀地分布到搜索空间中去,以增加粒子群的多样性和较强的开发能力,避免早熟;随着迭代次数的增加w,c1逐渐减小,c2逐渐增大,粒子群处于收敛状态,不断地跳出局部极值向全局极值靠拢;迭代后期的w,c1和c2趋于平稳,迭代处于多样化状态,种群具有较大开采能力,局部搜索能力增强。 图5 自适应参数调整策略曲线 最终得到Pareto解集在目标空间中的分布情况,如图6所示。 图6 Pareto前沿 由图6可见,Pareto前沿具有相当直观的均匀性,体现了算法既兼顾收敛性又不失多样性的特征,说明了基于Pareto熵的混沌自适应参数调整策略是有效的。通过模糊隶属度函数评价每个Pareto解,求出每个解的满意度值,选出满意度值最大的解作为最优方案,见表1。表中牵引变电所、分区所和AT所的最佳位置以线路公里标表示。 表1 满意优化方案中供电设施布局 为了验证上述优化方案的正确性和有效性,由牵引供电专业设计人员采用ELBAS/WEBANET软件(人工方案1)和传统的供电计算方法(人工方案2),分别独立给出牵引供电设计方案,3种方法的计算结果对比情况见表2。由于牵引变电所均采用中抽式单相变压器构成Vx接线方式,因此每个供电臂计算容量对应单相变压器原边绕组容量。表中Smax代表负荷过程中最大容量需求,Srms代表负荷过程对应的均方根值容量。由表2可见,利用多目标寻优模型,调整牵引变电所、分区所和AT所的布局,使得各供电臂的牵引负荷均衡性更好。以牵引变电所s1的供电区间为例,方案差异较大的原因分析如下。 (1)该区间位于山区长大坡道范围内,机车牵引特性决定了其持续满功率运行,如图4中牵引负荷曲线所示。为了保证接触网对地电压的约束条件,需要牵引供电系统提供足够的供电能力。因此,该牵引变电所内单相变压器的计算容量显著偏大。 (2)该区段桥隧比例较大,限制了各类型供电设施的设所条件。设计人员仅能依赖专业经验和主观判断,手动调整供电设施布置方案,缺乏可行域内全局搜索能力。优化算法则以目标函数满意度最大为收敛条件,通过不断调整优化变量的取值,沿着改善供电方案目标函数的趋势自动迭代。 不同设计方案在主要目标函数上也存在一定差异,对比结果见表3。由表3可见,满意优化方案中全线牵引变电所总计算容量最小,基于仿真计算软件得到的结果居中,传统手工供电计算方法得到的结果偏大。此外,满意优化方案中牵引供电系统的平均有功损耗也较小。造成上述差异的原因分析如下。 (1)既有牵引供电系统仿真计算软件仅能开展牵引负荷过程模拟,不具备设计寻优能力。本文通过将供电仿真与智能优化相结合,充分利用计算机强大的计算和高效的搜索能力,实现了多目标函数下的满意优化设计。 (2)传统供电计算方法一般取区间平均带电电流描述单车牵引负荷特性,在给定设所数目及所址的前提下计算供电容量,通过对有限供电方案的反复校核和比选,最终确定牵引供电方案。虽然简化了计算过程,但降低了计算精度,从而在一定程度上放大了供电容量需求和平均功耗。 表2 多种设计方案各变电所供电容量对比 表3 多种设计方案目标函数值对比 通过上述工程算例的分析,验证了本文提出的牵引供电系统多目标优化方法的正确性和有效性, 增强了最终方案的技术经济性。 以牵引供电系统主要设计原则作为约束条件,以全线总容量最小和平均有功功率损耗最小为目标函数,建立了牵引供电系统多目标优化模型。提出了基于Pareto熵的混沌多目标粒子群优化算法,结合模糊隶属度函数计算,使得目标函数尽可能达到最优,得到满意的优化设计方案。结合实际工程算例,对比既有设计方法,验证了上述模型和算法的正确性及有效性。 实际工程设计中除了技术和经济因素外,还需考虑社会因素和环境因素。在本文研究的基础上可以调整优化变量的可行域及约束条件,进一步完善多目标优化数学模型,提高寻优算法的效率,更好地满足电气化铁路牵引供电系统精细化设计的要求。 [1]陈民武,李群湛,智慧,等.牵引供电系统设计方案的综合评判[J].高电压技术,2010,36(2): 525-530. (CHEN Minwu,LI Qunzhan,ZHI Hui,et al.Comprehensive Evaluation for Design Scheme of Traction Power Supply System[J].High Voltage Engineering,2010,36(2):525-530. in Chinese) [2]BATTISTELLI L,PAGANO M,PROTO D.2×25-kV 50Hz High-Speed Traction Power System:Short-Circuit Modeling[J].IEEE Transactions on Power Delivery,2011,26(3):1459-1466. [3]吴命利.牵引供电系统电气参数与数学模型研究[D].北京:北京交通大学,2006. [4]陈宏伟,耿光超,江全元.电气化铁路牵引供电系统车网耦合的潮流计算方法[J].电力系统自动化,2012,36(3):76-80,110. (CHEN Hongwei, GENG Guangchao, JIANG Quanyuan. Power Flow Algorithm for Traction Power Supply System of Electric Railway Based on Locomotive and Network Coupling[J]. Automation of Electric Power Systems, 2012, 36(3): 76-80,110.in Chinese) [5]胡海涛,何正友,王江峰,等.基于车网耦合的高速铁路牵引网潮流计算[J].中国电机工程学报,2012, 32(19):101-108. (HU Haitao,HE Zhengyou,WANG Jiangfeng,et al.Power Flow Calculation of High-Speed Railway Traction Network Based on Train-Network Coupling Systems[J].Proceedings of the CSEE,2012,32 (19): 101-108. in Chinese) [6]宫衍圣.牵引供电系统优化设计技术的应用研究[D].成都:西南交通大学,2002. [7]汤庆峰,刘念,张建华,等.基于EMD-KELM-EKF与参数优选的用户侧微电网短期负荷预测方法[J].电网技术,2014,38(10):2691-2699. (TANG Qingfeng,LIU Nian,ZHANG Jianhua,et al.A Short-Term Load Forecasting Method for Micro-Grid Based on EMD-KELM-EKF and Parameter Optimization[J].Power System Technology,2014,38(10): 2691-2699. in Chinese) [8]沈玉明,胡博,谢开贵,等.计及储能寿命损耗的孤立微电网最优经济运行[J].电网技术,2014,38(9):2371-2378. (SHEN Yuming,HU Bo,XIE Kaigui,et al.Optimal Economic Operation of Isolated Microgrid Considering Battery Life Loss[J].Power System Technology, 2014, 38(9): 2371-2378. in Chinese) [9]陈民武.电气化铁路电能质量预测与对策分析研究[R].西安:中铁第一勘察设计院集团有限公司,2012. [10]陈民武, 尚国旭, 智慧, 等. 高速铁路牵引变压器容量与配置方案优化研究[J].中国铁道科学, 2013, 34(5):70-75. (CHEN Minwu, SHANG Guoxu, ZHI Hui, et al. Optimization on the Capacity and Configuration Scheme for Traction Transformer of High Speed Railway [J]. China Railway Science, 2013, 34(5):70-75. in Chinese) [11]中华人民共和国铁道部.TB 10009—2005 铁路电力牵引供电设计规范[S].北京:中国铁道出版社,2005. [12]刘文颖,谢昶,文晶,等.基于小生境多目标粒子群算法的输电网检修计划优化[J].中国电机工程学报,2013,33(4):141-148. (LIU Wenying,XIE Chang,WEN Jing,et al.Optimization of Transmission Network Maintenance Scheduling Based on Niche Multi-Objective Particle Swarm Algorithm[J].Proceedings of the CSEE,2013,33(4):141-148. in Chinese) [13]赵晶晶,李新,彭怡,等.基于粒子群优化算法的配电网重构和分布式电源注入功率综合优化算法[J].电网技术,2009,33(17):162-166. (ZHAO Jingjing,LI Xin,PENG Yi,et al.A Comprehensive Optimization Algorithm for Injection Power of Distributed Generation and Distribution Network Reconfiguration Based on Particle Swarm Optimization[J].Power System Technology,2009,33(17): 162-166. in Chinese) [14]胡旺,GARY G YEN,张鑫.基于Pareto熵的多目标粒子群优化算法[J].软件学报, 2014,25(5):1025-1050. (HU Wang,GARY G YEN,ZHANG Xin.Multiobjective Particle Swarm Optimization Based on Pareto Entropy[J].Journal of Software,2014,25(5): 1025-1050. in Chinese) [15]周孝法,陈陈,杨帆,等.基于自适应混沌粒子群优化算法的多馈入直流输电系统优化协调直流调制[J].电工技术学报,2009,24(4): 193-201. (ZHOU Xiaofa,CHEN Chen,YANG Fan,et al.Optimal Coordinated HVDC Modulation Based on Adaptive Chaos Particle Swarm Optimization Algorithm in Multi-Infeed HVDC Transmission System[J].Transactions of China Electrotechnical Society,2009,24(4): 193-201. in Chinese)
2.2 自适应混沌粒子群优化算法

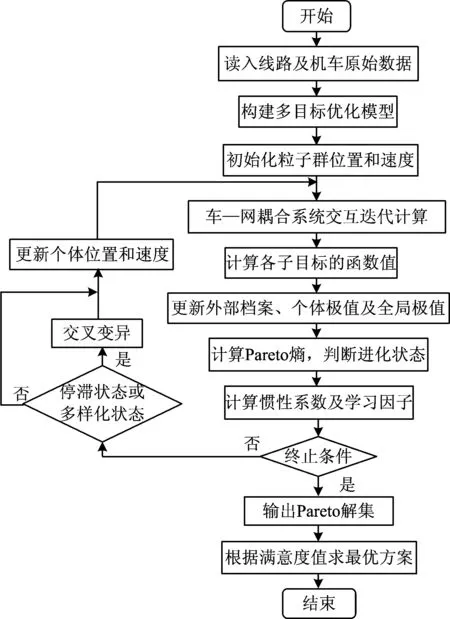
3 基于改进粒子群算法的牵引供电系统多目标优化过程
4 算例分析


5 结 语
