高速铁路隧道二次衬砌的变形特性与极限承载能力

孙　毅，张顶立，于富才，王剑晨，黄　俊

(1.北京交通大学 城市地下工程教育部重点实验室，北京　100044；2.北京城建集团有限责任公司，北京　100088；3.苏交科集团股份有限公司，江苏 南京　210017)

目前铁路隧道二次衬砌的设计仍主要根据围岩级别和地形条件，采用破损阶段法进行衬砌结构验算，再通过工程类比，并结合施工条件等确定设计参数，其本质仍延续了传统铁路隧道的设计理念，与新奥法理念还有不少差距。

现阶段关于隧道二次衬砌的研究主要集中在支护时机、结构优化、裂缝以及可靠度分析等方面[1-3]，其研究成果为研究高速铁路隧道二次衬砌的变形特性与极限承载能力打下了坚实的基础。同时，相关学者[4-6]认为，对岩性较好、完整性高的Ⅱ和Ⅲ级围岩、二次衬砌并非是必选项，可以视具体情况只做锚喷支护或单层衬砌，而对于相对破碎的Ⅳ，Ⅴ和Ⅵ级围岩，将二次衬砌“减薄”也是可行的。但是这些研究对“减薄”的论证依据不充分，其中二次衬砌的承载特点如何，其承载能力究竟有多大，钢筋和混凝土材料的性能如何发挥等等，都没有给出具体的答案。

因此，本文通过分析TB10003—2005《铁路隧道设计规范》[7](以下简称《规范》)的局限性，以Ⅴ级围岩，350 km·h-1速度的高速铁路隧道(简称为350 km·h-1—Ⅴ级隧道)为例，采用MIDAS—NX软件，建立“拟地层—结构”模型，通过研究二次衬砌的变形特性和极限承载能力，对上述问题进行解析。

1　现行《规范》科研应用的局限性

《规范》对现阶段各项设计工作的指导意义毋庸置疑。但随着认识的深入与研究手段的进步，《规范》在极限条件下的科研应用出现了一定的局限性。

1.1　拱状混凝土衬砌的特殊边界条件

现行《规范》中关于二次衬砌结构的力学模型及其内力平衡方程，基本移植了工民建中钢筋混凝土受压构件(梁、板、柱)的，这样的移植实际上忽略了如图1所示的隧道二次衬砌构件与工民建受压构件的边界条件差异。

由图1不难看出：在隧道二次衬砌构件中，围岩起到了“荷载边界”的作用，构件的变形趋势是由接触压力P、轴向力N、弯矩M共同决定的；而工民建受压构件模型并不存在这样的边界条件，构件的变形趋势是由轴向力N和弯矩M共同决定的；隧道二次衬砌构件中有一部分区域处于三轴受压的应力状态，而工民建受压构件则接近于无侧限的单轴受力状态。由此可见，隧道二次衬砌构件的受力状态实际上要优于工民建受压构件。

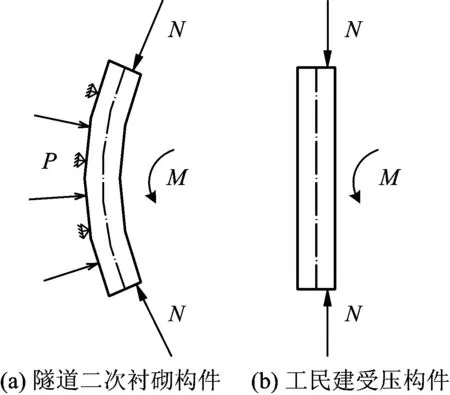
图1　隧道二次衬砌构件与工民建受压构件的边界条件示意图

工民建受压构件的平衡方程是由轴向力N平衡和弯矩M平衡2个等式构成的，采用单轴抗压和抗拉强度基本可以满足求解方程的需求。而对于隧道二次衬砌构件，若同样应用单轴抗拉和抗压强度求解其平衡方程，显然难以与其受力状态相适应，并且结果偏大。另一方面，从已有的研究成果[8-9]易知，混凝土材料的单轴抗压强度远低于三轴抗压强度，换而言之，隧道二次衬砌结构对混凝土材料强度的利用率更高。

1.2　二次衬砌结构破坏的判定

现行《规范》判断二次衬砌结构的破坏，本质上是采用单一截面的平衡条件与安全系数的组合进行的。事实上，完整的隧道二次衬砌拱形结构可以视为三次超静定无铰拱结构。当其中一部分发生破坏出现塑性铰时，则转换为两铰拱，此时结构变为一次超静定体系；再产生一个塑性铰，衬砌结构进入三铰拱阶段，这时的结构仍为静定体系；但若发生进一步的破坏，产生更多的塑性铰，结构将变为不稳定的机构，即结构进入破坏的临界状态，随时可以发生大变形。如图2所示。可见拱结构的破坏并非一蹴而就，而是逐渐发展形成的。

张素磊[10]等通过实测数据统计与模型试验进一步印证了：拱形结构(厚壁)的破坏并非是单一界面的破坏造成的，甚至在多界面发生断裂时仍可以保持拱状形态而不坍塌。

因此，判断隧道二次衬砌结构破坏的临界状态时，不能仅依靠单一界面，这样过于“安全”，应以加载过程中二次衬砌结构快速变形阶段作为标准才更为合理；此外，这时收敛计算会失效，各项数据结果跳跃明显，以此作为判据也十分直观。

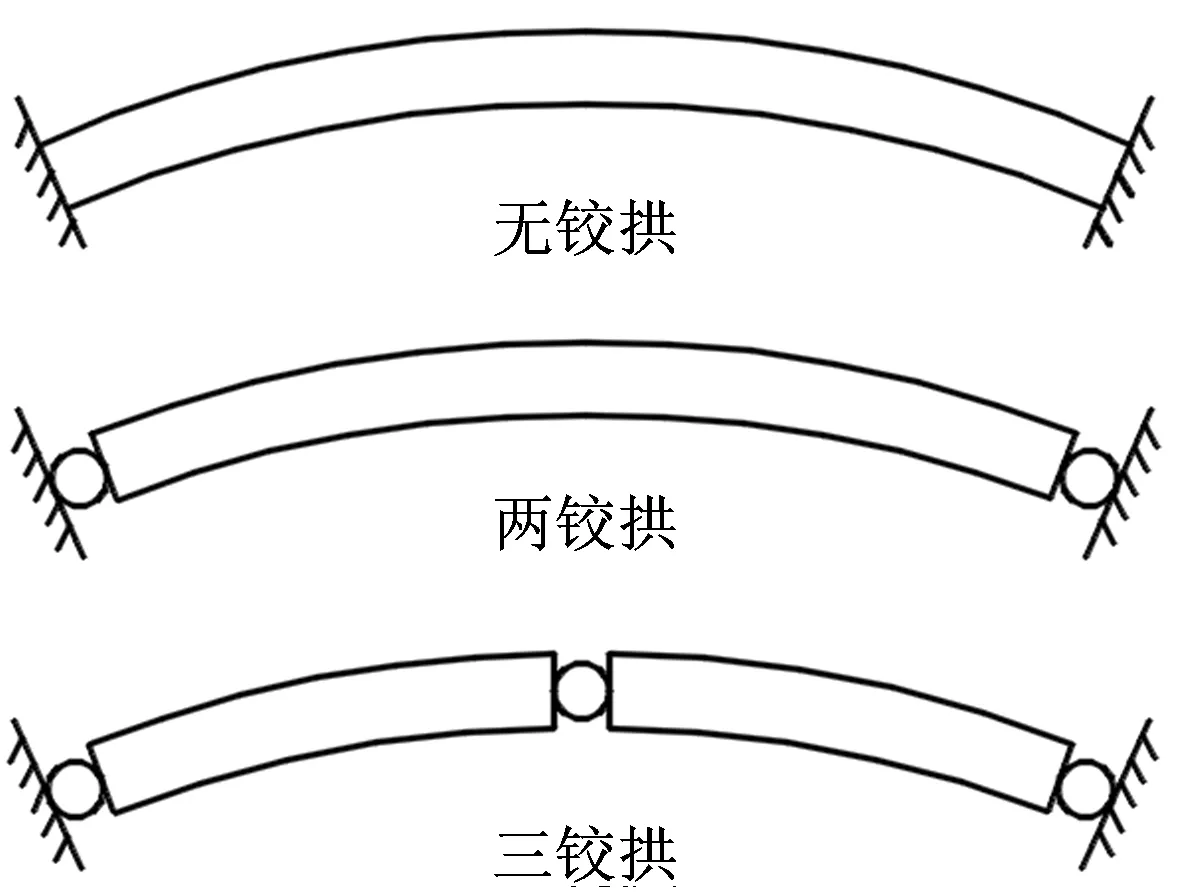
图2　拱形构件破坏发展示意图

2　“拟地层—结构”模型的建立与参数选取

2.1　模型的建立

考量二次衬砌极限承载能力离不开对其受载模式的准确描述。衬砌结构的受载模式不仅取决于自身的几何形式，更要受到初始地应力条件的影响以及其加、卸载方式的限制，如何真实地还原衬砌结构在围岩中的受载状态，已成为衬砌结构模拟计算的关键问题之一。

从郑颖人等[11]的研究中不难看出，软土隧道与岩质隧道荷载分布是不同的，尤其在拱顶处甚至出现了相反的规律，软土隧道上方形成了应力集中，岩质隧道上方的竖向应力反而减小，这是由于围岩的物理力学参数(特别是围岩的弹性模量、内聚力和内摩擦角)不同，在隧道上方形成了卸荷拱。也就是说荷载结构法并不能很好地反映隧道衬砌的受载状态。相对而言，地层结构法能更好地体现衬砌的受载状态，其先进性在于反映出了地下结构工程与围岩的相互作用，不足之处在于对岩土体本身性质的一些参数选取始终难以令人信服，因此在实际工程中运用也很少，仅作为设计参考使用[12]。

从本质上讲，上述2种方法都是为了营造较为真实的围岩应力状态。而本文重点研究的是二次衬砌结构的变形和破坏，围岩的响应并不在研究范畴之内。在此前提下，可以只把围岩模型当做加载过程中的传力工具，在加载阶段将其设置为理想弹塑性体，相关参数取值参考《规范》中Ⅴ级围岩的描述(弹性模量E=1.2 GPa，泊松比ν=0.4，黏聚力c=0.1 MPa，内摩擦角φ=24°)，通过应力边界设置初始地应力，不考虑岩石的容重参数；在开挖洞室释放应力阶段，再将围岩设置为弹性体，弹性模量E参考Ⅴ级围岩的抗力系数(K=120 MPa)重新进行设置。

以上操作既避免了围岩弹塑性带来的影响，又较为真实地反映了围岩对隧道二次衬砌结构的荷载和约束作用，很好地集合了“荷载结构法”与“地层结构法”的优点。现将这种加、卸载方式下的模型定义为：拟地层—结构模型。

采用MIDAS—NX软件实现建模与计算。断面参考350 km·h-1—Ⅴ级隧道。数值模型的长宽边界分别为120 m×120 m，洞室位于中心，厚度方向取1 m。右、下部为位移边界；左、上部为荷载边界。接触单元为无厚度的二维单元，主要用于监测二次衬砌单元的受力状况，不承担荷载。岩土体与二次衬砌(C30混凝土)采用实体单元。由此建立的三维数值模型如图3所示。

图3　数值模型示意图

二次衬砌的配筋细节如图4所示，其中环向主筋φ22@200、纵向钢筋φ14@250、径向构造筋φ8。主筋采用HRB335螺纹钢，纵筋和构造钢筋采用HPB235圆钢。

图4　模型中钢筋空间布置图

采用建立的“拟地层—结构”模型进行数值模拟的具体计算步骤为：①模型边界位移约束+施加外荷载；②位移清零；③撤除外荷载+锁定边界；④开挖洞室轮廓+施作衬砌结构；⑤观测变形及破坏现象。特别需要说明的是，在步骤④中，模型右、下部仍为位移边界，而左、上部也变为了位移边界，并进行锁定。

一般情况下，若采用全荷载(对称加载)直接约束的模式进行模拟，往往会出现单元刚度矩阵奇异的现象，其原因是模型整体在无位移约束的前提下，将在不平衡力的驱使下发生刚体位移；因此必须对模型施加一定的位移约束，而施加位移约束后衬砌模型位移一般就包含了模型整体压缩和卸载变形这2个量，在提取数据时难以区分，常常导致衬砌变形结果过大。而本文建立的上述模型，在后处理的计算中只保留了衬砌卸载变形部分，很好地避免了这一问题。

2.2　侧压力系数的变化范围

在二次衬砌结构形式确定的前提下，侧压力系数集中体现了初始地应力的分布特点，对变形结果起到了决定性作用。童景盛等[13]通过对国内外多条隧道侧压力的量测得出结论：不论是石质还是土质隧道，其侧向压力均是比较大的，侧压力系数基本都在0.6～1.0之间。关宝树[14]等统计了日本、欧美等其他地区的大量测量数据，总结了侧压力系数与埋深的关系，认为侧压力系数可能在0.4～2.0之间变化，在大多数深埋场合(埋深大于50 m)侧压力系数为1.0。徐干成等[15]认为：侧压力系数一般为0.8～3.0，大部分在0.8～1.2之间。但也有地震、冲击矿压(岩爆)、构造运动等极端条件下水平应力急剧增大的情况[17]。综上所述，本文取侧压力系数λ=0.1，0.2，0.3，…，2.0，3.0，5.0，8.0，10.0，共计24个数值，并由此划分为24个工况。

2.3　摩尔库伦强度准则下的混凝土强度参数

二次衬砌结构采用摩尔库伦本构模型，目前《规范》仅提供了混凝土材料的单轴强度，为了得到不同混凝土材料的摩尔库伦强度参数，则需要利用这些数据进行转换。

首先应明确的是理论上破坏面(failure surface)和屈服面(yield surface)是不同的，混凝土试件在高静水压力作用下会发生相当的塑性变形，表现为屈服，但没有破坏。而工程上又常将二者等同，其原因是工程结构不容许有很大的塑性变形，且混凝土等材料的屈服点不够明确，但破坏点非常明确，因此可以借用破坏准则近似判断屈服。

就强度包络线形式而言，主要有摩尔库仑斜直线和莫尔抛物线两类。不同的岩石、土和混凝土结构，据其不同的受力状态，具有不同的破坏模式。一般土体和较软弱岩石(如泥岩、页岩等)的强度包络线近似于二次抛物线形；混凝土和较坚硬的脆性岩石以剪切破坏或张拉破坏为主，强度包络线呈斜直线型[17-18]，如图5所示。图5中：σ为切应力；τ为剪应力；σc为混凝土单轴抗压强度；σt为混凝土单轴抗拉强度。

在图5中有

(1)

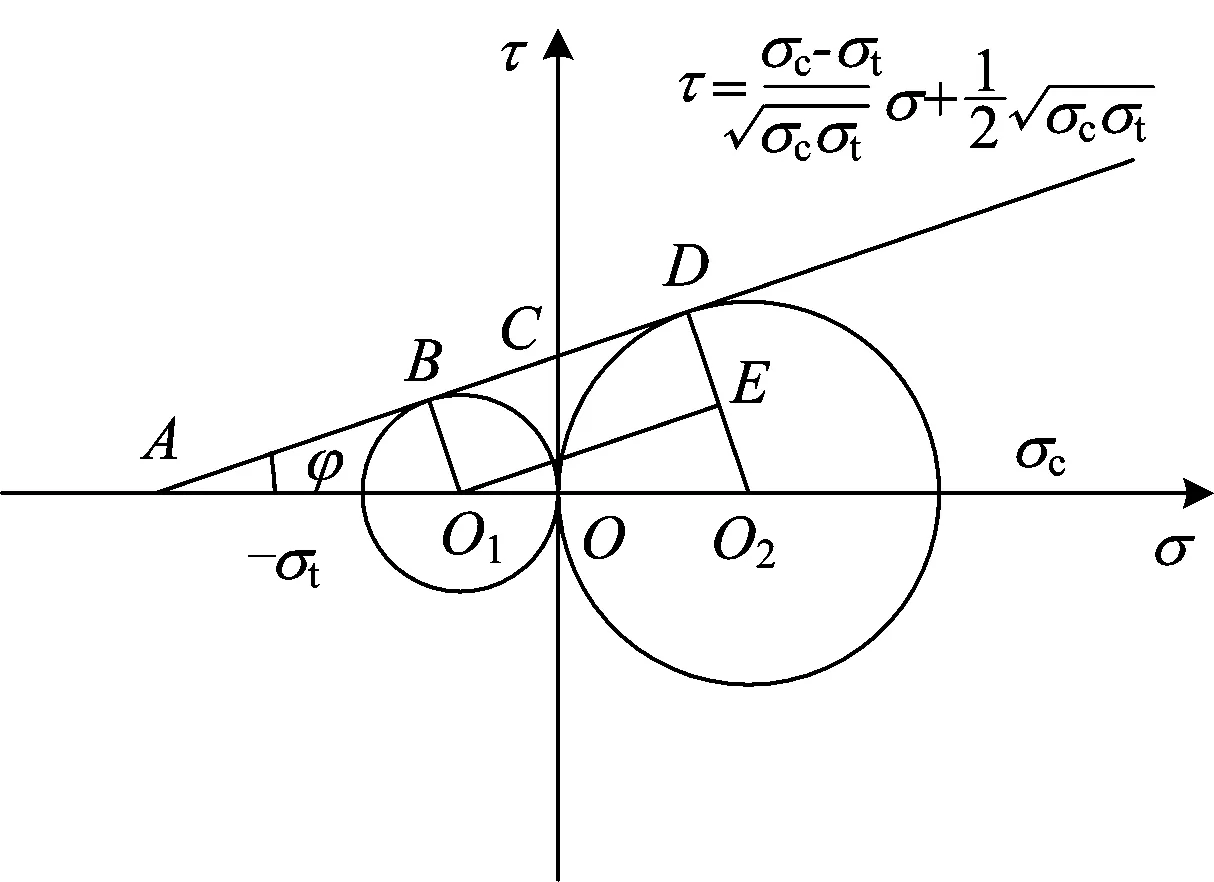
图5　斜直线型摩尔库伦破坏准则

根据Rt△O1EO2≌Rt△ADO2可知

(2)

(3)

则斜直线方程可以表述为

(4)

根据式(1)—式(4)可得

(5)

(6)

利用《规范》提供的混凝土单轴抗压强度σc和抗拉强度σt的标准值，采用式(5)和式(6)可换算得到不同标号混凝土的内摩擦角φ和黏聚力c，见表1。

表1　混凝土强度参数换算表

3　数值试验结果分析

3.1　隧道二次衬砌结构的变形特性、受力特性

由模拟结果可知，破坏临界状态(收敛计算模式失效状态)时，在不同的侧压力系数条件下，二次衬砌结构的变形模式差异很大，随着侧压力系数的逐渐增大，二次衬砌结构变形模式为由 “扁平”逐渐到“直立”。这里选取变形模式发生突变的3种工况(λ=0.8，2.0，5.0)时的洞形，以及第1工况(λ=0.1)和第24工况(λ=10.0)时的洞形、原始洞形绘制成图6。

图6　临界破坏状态下二次衬砌结构的洞形

将模拟结果与原始洞形比较可知：当侧压力系数λ<0.8时，二次衬砌结构变形模式为“竖向压缩+横向扩张”；当0.8≤λ<2.0时，二次衬砌结构变形模式为“整体压缩”；当λ≥2.0时，二次衬砌结构变形模式为“竖向扩张+横向压缩”，但此时竖向扩张集中在拱顶部分，仰拱仍处于压缩收敛状态，待λ>5.0时，仰拱也会出现纵向扩张的现象。

二次衬砌结构的变形连续性较强，但不同的区域又存在着不同的变形和受力特点，为了方便分析，根据三圆制图法将该二次衬砌结构整个断面的曲率分为如图7所示的4个部分。

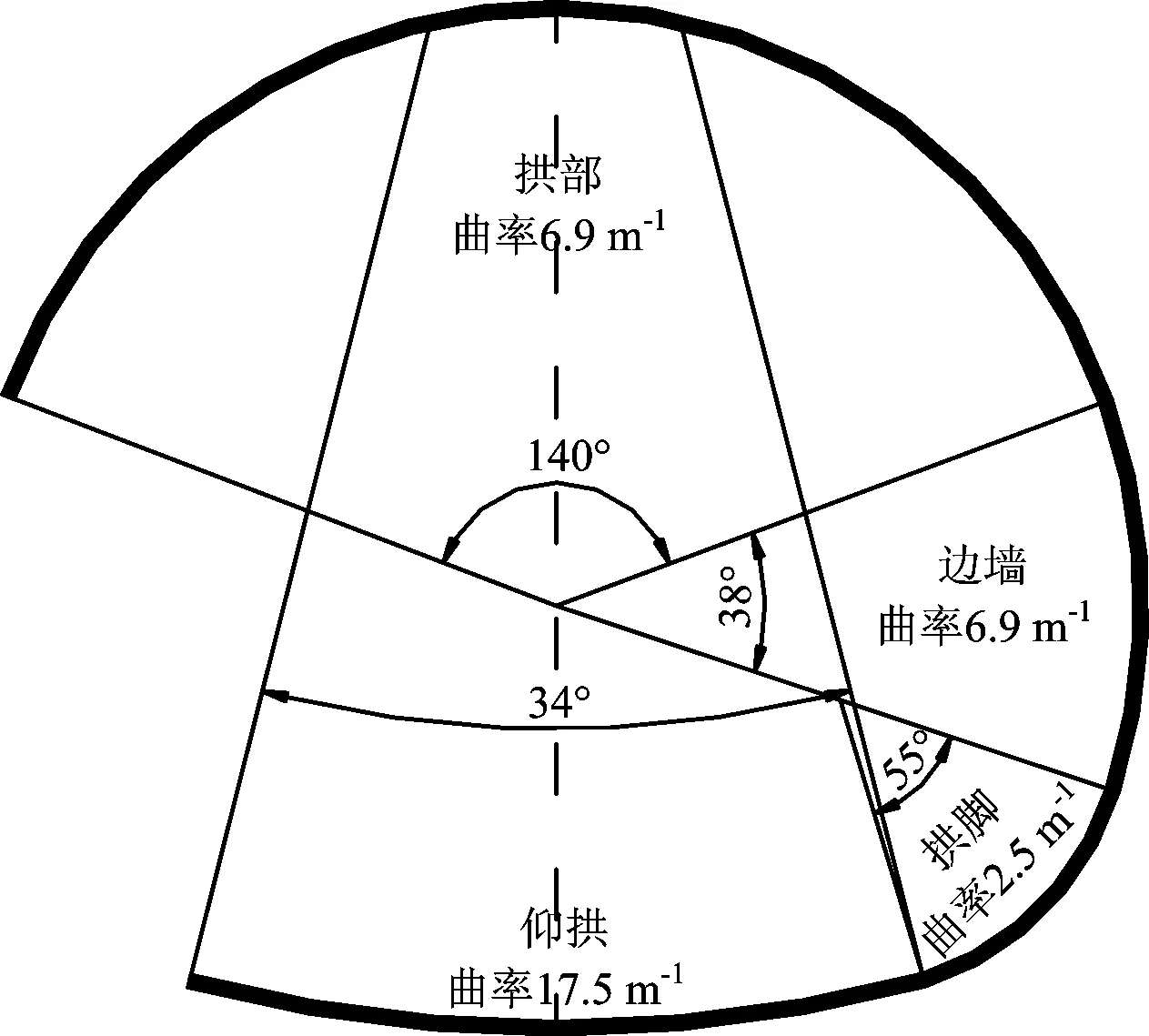
图7　二次衬砌原始曲率

根据铁木辛柯梁理论易知：拱形结构的曲率变化可以反映出厚壁拱结构的内外侧受力特点。因此，将临界破坏状态时不同工况条件下该二次衬砌由拱顶至仰拱的曲率列于表2。

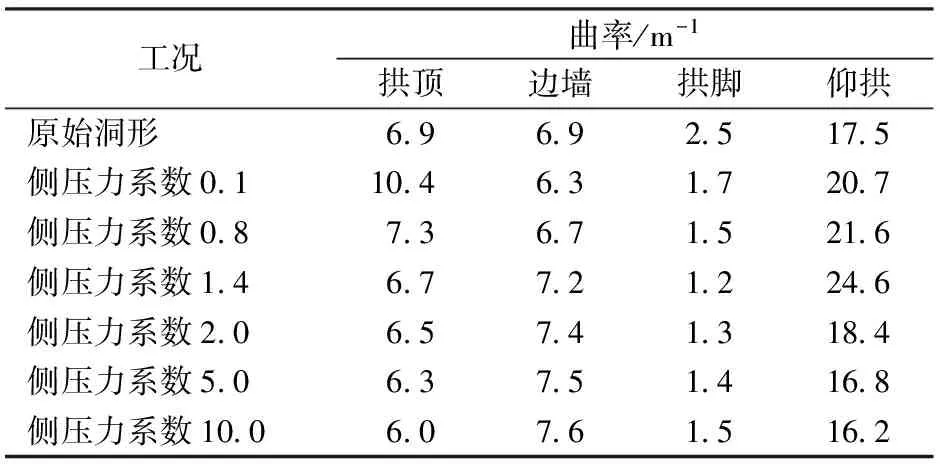
表2　临界破坏状态时二次衬砌的曲率变化

分析图7和表2可得如下结论。

λ=0.8时，二次衬砌结构的两侧超出原始界线，拱顶与仰拱侵入原始界线；拱腰和边墙以内侧受压、外侧受拉为主；拱顶与仰拱以内侧受拉、外侧受压为主。

λ=2.0时，二次衬砌结构的两侧、仰拱均侵入原始界线，拱顶与原始界线齐平；拱腰和边墙以内侧受拉、外侧受压为主；拱顶与仰拱以内侧受压、外侧受拉为主。

λ=5.0时，二次衬砌结构的两侧侵入原始界线，拱顶超出原始界线，仰拱与原始界线齐平；拱腰和边墙以内侧受拉、外侧受压为主；拱顶与仰拱以内侧受压、外侧受拉为主。

对于其余工况，其二次衬砌结构的变形和受力均在上面3个工况所分隔开的区域内连续变化，在此不再赘述。

3.2　二次衬砌结构塑性区发展特点

塑性区的出现与发展显示了二次衬砌结构的薄弱环节，因此是施工监测、补强加固的关键区域。在二次衬砌的受载变形过程中，随着侧压力系数的逐渐增加，塑性区的产生区域及发展方向分为以下3个阶段。

(1)在低侧压力系数(0.1≤λ<0.8)下，随着荷载的增加，首先在拱脚出现塑性区，并主要是压剪塑性；然后塑性区向上扩展，结构内侧以压剪塑性为主、外侧以张拉塑性为主，在拱顶内侧亦出现了张拉塑性区；最后，在结构接近破坏时，仰拱产生了一定量的内压外拉的塑性区，先前产生的各种塑性区也有了不同程度的发展。其代表性的演化规律如图8(a)所示。

(2)在高侧压力系数(0.8≤λ<2.0)下，随着荷载的增加，首先在拱脚与拱腰内侧出现塑性区，其中拱脚为压剪塑性，拱腰内侧为张拉塑性；然后，拱腰以及边墙部分的塑性区得到了一定的发展，此时结构内侧以张拉塑性为主，外侧以压剪塑性为主，这与图8(a)恰好相反，在拱顶外侧亦出现了张拉塑性区；最后，在结构接近破坏时，仰拱产生了内压、外拉的塑性区，先前产生的各种塑性区也有不同程度的发展。其代表性的演化规律如图8(b)所示。

(3)在超高侧压力系数(λ≥2.0)下，随着荷载的增加，首先在拱顶出现塑性区，以压剪塑性为主但范围较小，拱脚紧随其后，以内侧压剪塑性为主并伴随少量外侧张拉塑性区；然后，边墙、拱腰内侧及拱脚外侧均出现了大量的张拉塑性区；最后，在结构接近破坏时，仰拱产生了内压、外拉的少量塑性区，先前产生的各种塑性区也有了不同程度的发展。其代表性的演化规律如图8(c)所示。

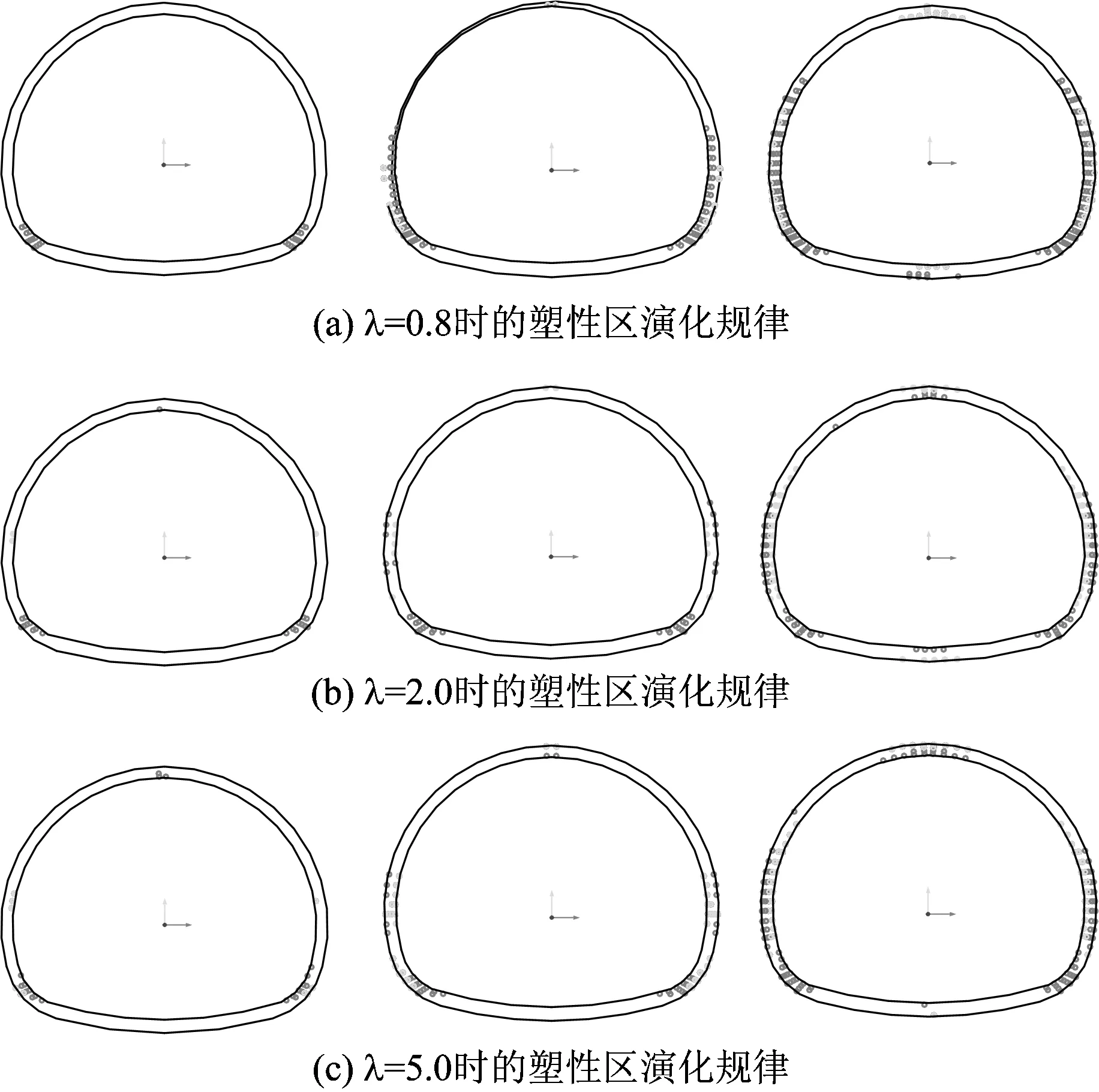
注：○代表受拉屈服，●代表受压屈服。

在二次衬砌结构受载达到极限状态时统计拉、压塑性区的面积可知：塑性区面积沿隧道环向(拱顶、拱腰+拱墙、拱脚)的分布比例约为2∶5∶3，而塑性区往往会连通成为塑性铰，最终形成实际工程中的张拉裂缝或压碎裂缝[19]。本文认为拱脚处塑性区面积的比例大于拱顶处，这与既有的研究结论略有不同，既有的研究资料中很少提及这一现象，大都认为拱顶和边墙处产生的塑性区大于拱脚处。如文献[20—21]通过实测统计，认为拱顶处的裂缝占了更大的比例。产生这一现象的主要原因是实际工程中拱顶处受到注模工艺的影响，接触不实的情况大量存在,文献[22—24]也认为不良受力状态会影响拱顶处的受力[22-24]，出现裂缝的概率将随之加大。出现这种现象的主要原因归结起来有以下3点。

(1)隧道的水沟、电槽等附属结构覆盖在隧道二次衬砌拱脚之上，隐藏了拱脚裂缝，直接观察和雷达探测都难以发现。

(2)整浇轨道板、仰拱及其回填层的存在能够增加隧道仰拱的整体刚度与自重，同时减小了仰拱的隆起量，改善了二次衬砌拱脚的受力状态，从而减少了塑性区。

(3)超挖隧道的拱脚外部回填层联合初期支护可以形成一个坚实的隅角结构，进而缓解了二次衬砌在拱脚处应力集中的问题，同样可以减少塑性区数量。

3.3　二次衬砌结构极限承载能力的评价

事实上，二次衬砌结构的极限承载能力并不能用1个确定的荷载值表征。从数值试验结果看，二次衬砌结构在破坏的临界状态下，其周围的荷载是很复杂的，准确地说应该是与二次衬砌形状相关的一圈闭合荷载函数。这与圆形洞室理想状态下开挖后得到的弹性解不同，也与荷载结构法中垂直压力+水平荷载的组合形式不同。

二次衬砌结构的破坏临界状态可以用多种参数进行描述，而且参数越多越接近真实，但受到测量手段的限制，参数的数量不可能太多。为了方便实际工程的应用，本文提出基于3组参数的二次衬砌结构破坏临界状态包络曲线，用于判断二次衬砌结构是否达到破坏临界状态。这3组参数为衬砌单元的剪应力τ、接触压应力p(围岩和初支复合体对二次衬砌的压力)和径向位移u。

破坏临界状态下不同侧压力系数时衬砌单元的平均剪应力和平均接触压应力如图9所示。

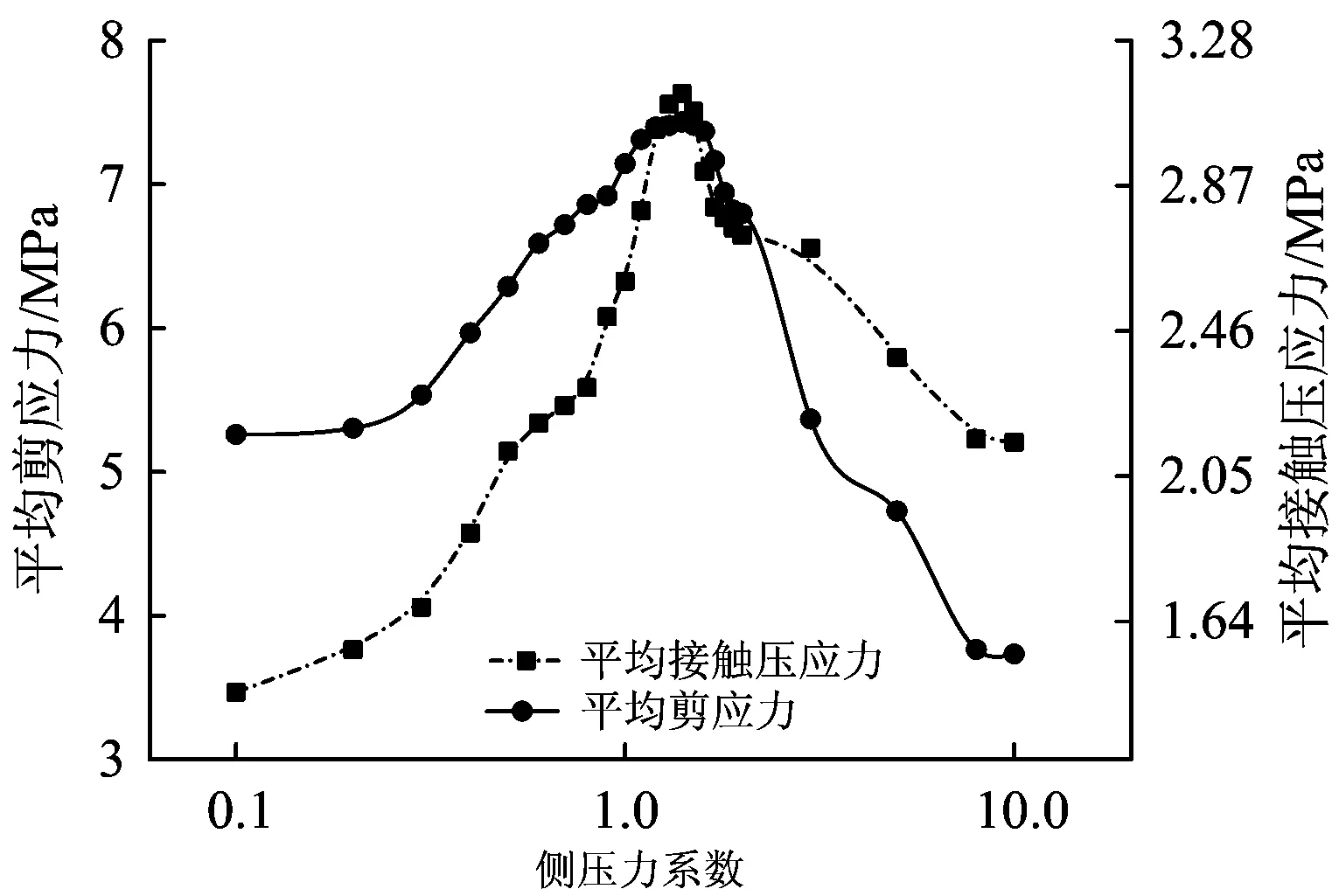
图9　破坏临界状态下不同侧压力系数时衬砌单元的平均剪应力和平均接触压应力

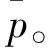
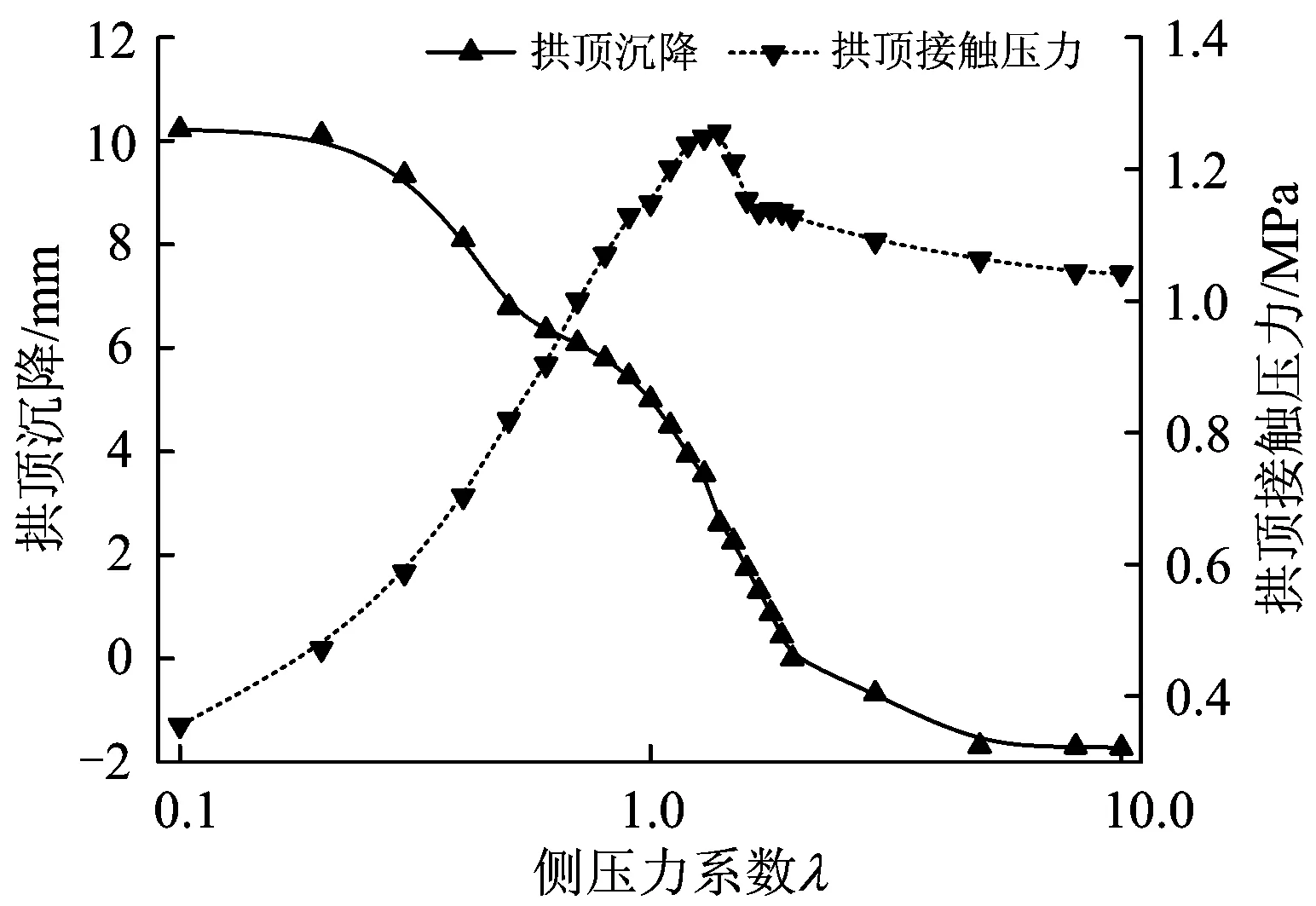
图10　破坏临界状态下不同侧压力系数时拱顶的沉降及其接触压应力

从图10中的拱顶沉降曲线可以看出：随着侧压力系数的增加，在λ=2.0附近，拱顶沉降由正值转为负值，即当侧压力系数达到2.0以后，拱顶不再下沉而是逐渐向上隆起。这样的变形对于拱顶存在空洞的衬砌结构而言是极为不利的，特别容易产生内侧压缩、外侧张拉的裂缝[25]，应该引起注意。

综上分析可以得出，对于高速铁路隧道350 km·h-1—Ⅴ级断面的二次衬砌，只有在λ=1.4时，其承载能力才达到最大，而不同于通常的深埋圆形隧道是在λ=1.0时其承载能力达到最大。因此可以认为：只有断面形式、侧压力系数达到合理的匹配才能充分发挥衬砌结构的承载能力，或者说才有可能出现真正的承载极限状态。

3.4　钢筋的存在对隧道二次衬砌承载能力的影响

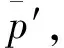
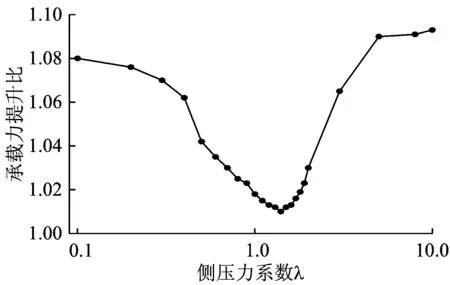
图11　在不同侧压力系数下钢筋对隧道二次衬砌结构承载力的提升比

由图11可以看出：无论何种侧压力系数下，钢筋都能够一定程度地提升二次衬砌结构的承载能力；但当侧压力系数达到λ=1.4左右时，钢筋对二次衬砌结构承载能力的影响最小，侧压力系数愈远离λ=1.4，钢筋的作用愈加明显，曲线整体呈现“V”字形。

以侧压力系数λ=2.0工况为例，分析钢筋对衬砌单元第一主应力与第三主应力的影响，如图12所示。由图12可以得出：拱腰至拱脚外侧的平均第一主应力(压)提高了6%，内侧的第一主应力(拉)降低了18%；而各位置平均第三主应力(压)提高了不到3%，说明钢筋的存在主要影响衬砌单元的第一主应力(拉)；这是因为通过钢筋对衬砌结构受拉区的约束，改善了衬砌结构的受压区状态，进而提高了初砌结构整体的承载性能。

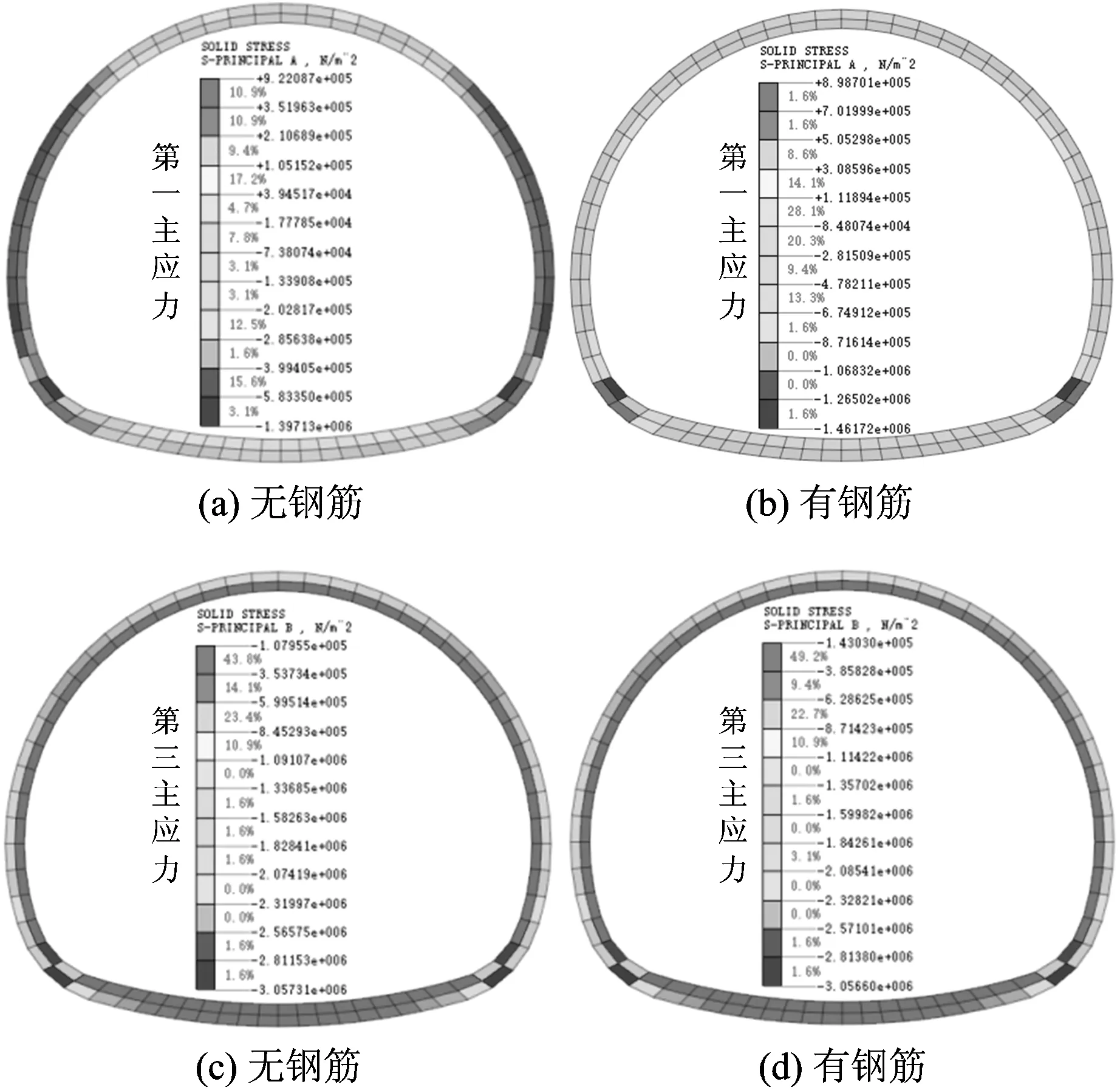
图12　λ=2时钢筋对主应力的影响

结合图3不难得出：加入钢筋后，衬砌单元的应力圆通过缩小直径的方式远离了破坏临界状态线，从而可能获得了更大的承载；此外，钢筋对衬砌单元应力的均匀化分布也起到了一定的促进作用，这也使得局部应力集中的现象得到了改善，从而减少了因塑性区连通引起失稳的可能性。

由此可以解释图11中反映的侧压力系数λ=1.4左右时钢筋对二次衬砌结构承载能力的影响最小的结果，这是因为当λ=1.4时，衬砌结构的拉、压性能较为均衡，所以此时钢筋对承载力的提升作用才不明显。

4　实测数据对比

本文统计了36座高速铁路隧道中66个监测断面的二次衬砌接触压力，其中大多数集中在拱顶及边墙，对其整理后得到的应力分布规律分别如图13和图14所示。

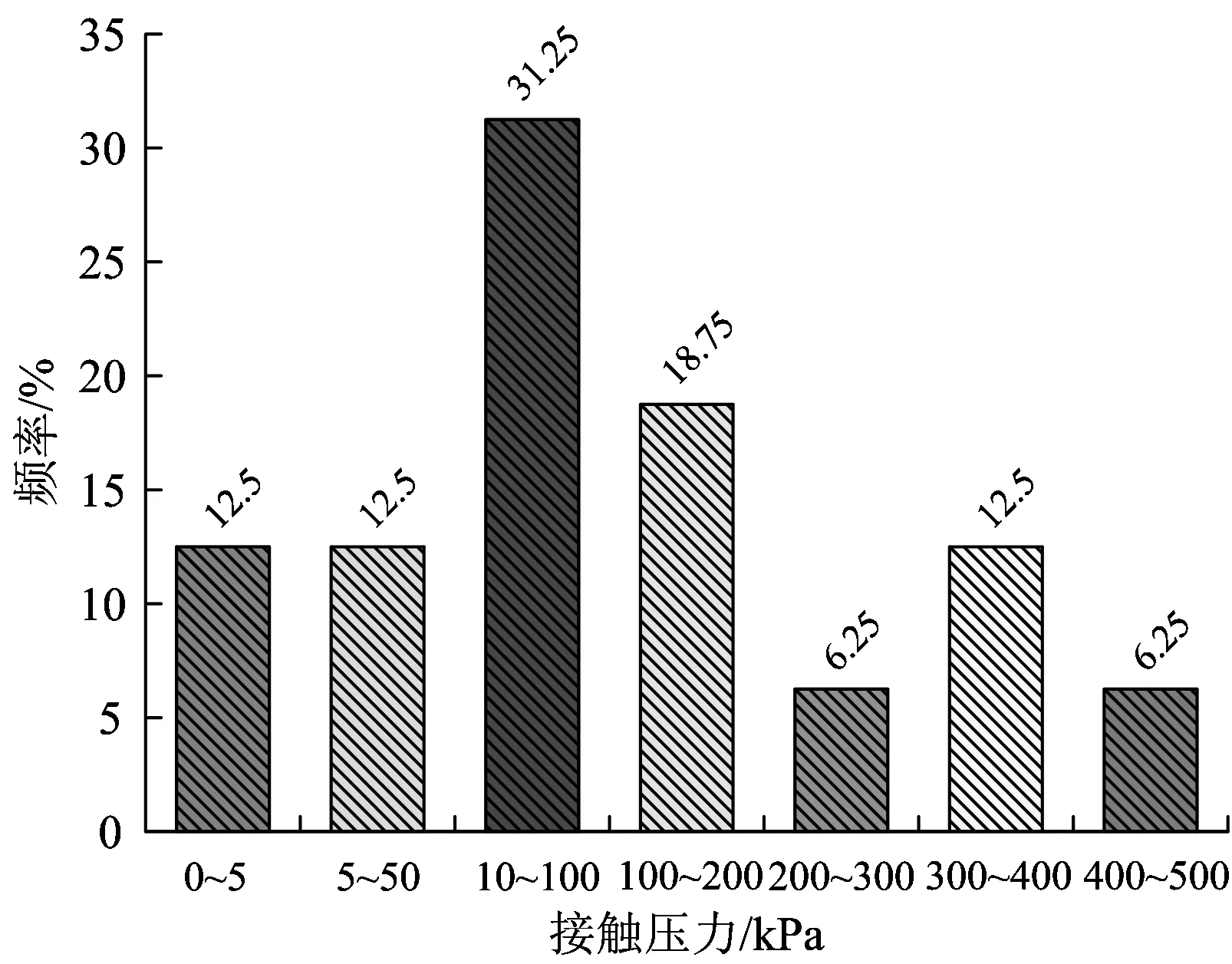
图13　二次衬砌拱顶接触压力—频率直方图

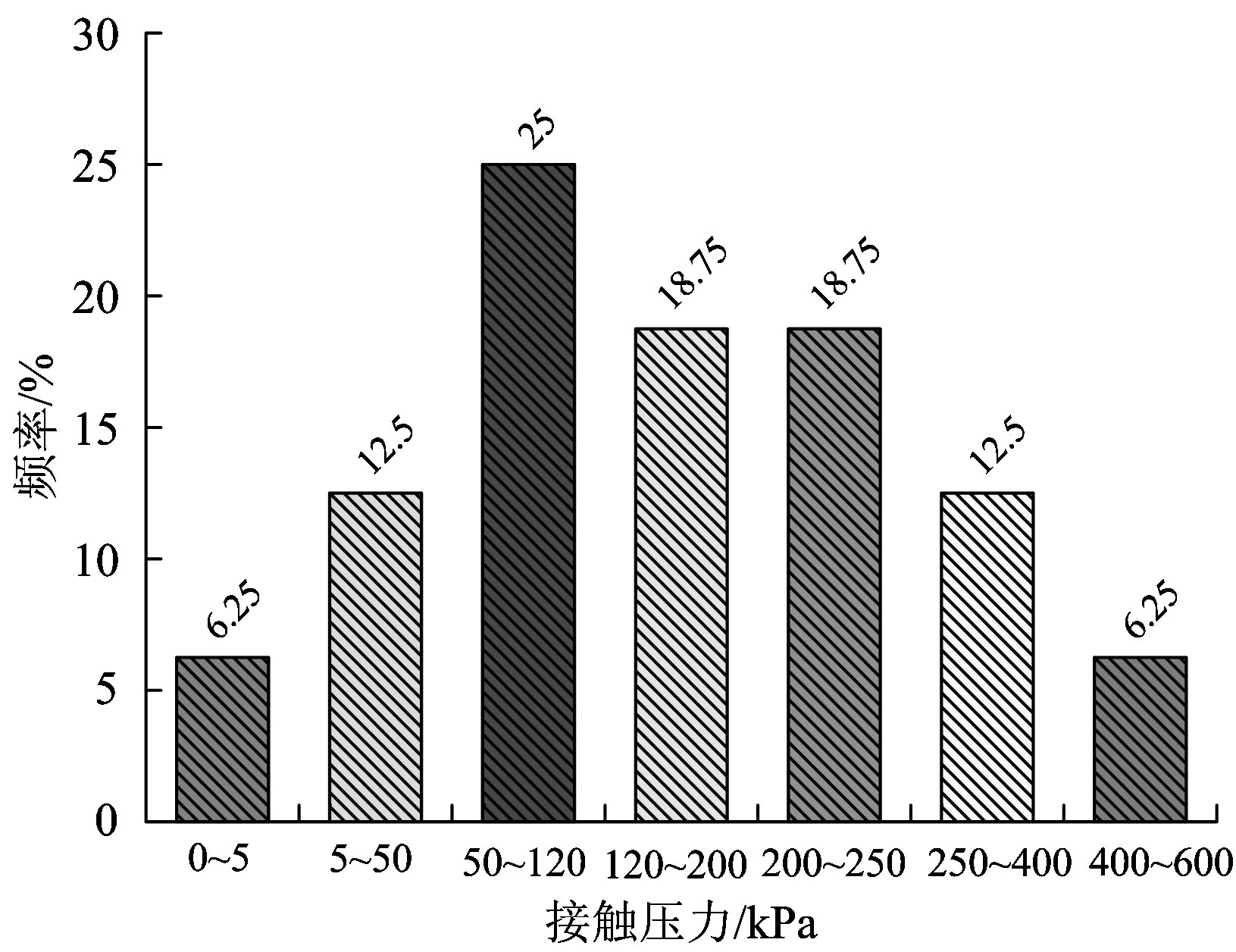
图14　二次衬砌边墙接触压力—频率直方图

从监测数据来看，二次衬砌的接触压力大都集中在50～400 kPa之间，最大值约为600 kPa。在数据较为完整的监测结果中选取3组侧压力系数与数值模型相近的接触压力，将其与模拟结果进行比较，如图15所示。并将这6种工况下的不同接触压力列于表3中。

图15　实测的接触压力分布与数值模拟的接触压力分布对比(单位：kPa)

表3　接触压力对比表

由图15和表3可知：在侧压力系数较小时，实测结果与数值模拟结果最为接近；实测结果中，贵广线棋盘山隧道二次衬砌的接触压力大于其他2个隧道，而其侧压力系数λ=1.6，这一特点与上文的模拟分析结果相符；实测的高速铁路隧道二次衬砌受载量远小于其极限能承载力，将这3组数值的模拟结果分别与实测结果相比，在最大接触压力上前者分别是后者的7.8，12.5，10.5倍，在拱顶接触压力上前者分别是后者的14.2，5.3，10.5倍，在平均接触压力上前者分别是后者的13.3，14.4，10.5倍。

由此可见，设计的二次衬砌有着足够的储备量，其承载能力远远超过了其实际所需要的。这样超饱和的安全设计，反而容易忽视实际施工过程中的初衬环节，如往往将初期支护当作简单的临时支撑，等待施作二衬来分担荷载，从而造成施工过程中的偷工减料。这种对二次衬砌的依赖，与新奥法理念是矛盾的，另一方面，若出现对围岩变形时空效应掌控不当，将可能导致塌方冒顶事故，从而威胁隧道施工的安全。因此，可以对高速铁路隧道二次衬砌进行“减薄”。

5　结　论

(1)在归纳分析《铁路隧道设计规范》中二次衬砌结构与普通受压结构在边界条件、平衡方程方面存在差别的基础上，认为采用单轴抗拉、抗压强度作为判断高速铁路隧道二次衬砌材料破坏的参数过于安全。提出了350 km·h-1—Ⅴ级高速铁路隧道断面二次衬砌的“拟地层—结构”模型，并推导出了摩尔库伦斜直线强度准则下混凝材料强度参数与单轴强度的换算关系。

(2)明确了高速铁路隧道二次衬砌结构的变形、受力特点及塑性区发展均与侧压力系数有关；在侧压力系数λ=1.4时，350 km·h-1—Ⅴ级高速铁路隧道断面二次衬砌的承载效果最佳。

(3)高速铁路隧道二次衬砌中钢筋主要起控制衬砌单元第一主应力(拉应力)的作用，并在侧压力系数偏小和偏大条件下的作用效果最为明显。

(4)选取36座高速铁路隧道的66个监测断面，统计分析了二次衬砌的接触压力，并将监测结果与数值模拟结果进行对比分析，发现实测的高速铁路隧道二次衬砌受载量远小于其承载极限能力。因此，可以对高速铁路隧道二次衬砌进行“减薄”。

[1]王长辉. 公路隧道二次衬砌受力及结构优化设计研究[D]. 西安: 长安大学, 2012.

(WANG Changhui. Study on Stress and Optimization Design of Secondary Linings in Highway Tunnel [D]. Xi’an: Chang’an University, 2012. in Chinese)

[2]腾宏伟. 隧道特殊大变形段初支开裂机理及二次衬砌结构可靠度研究[D]. 重庆: 重庆大学, 2008.

(TENG Hongwei. Study on the Initial Support Crack Mechanism and Secondary Lining Structure Reliability in the Especial Large Deformation Zone of Tunnel[D]. Chongqing: Chongqing University, 2008. in Chinese)

[3]刘志春, 李文江, 朱永全，等. 软岩大变形隧道二次衬砌施作时机探讨 [J]. 岩石力学与工程学报， 2008, 27(3): 580-588.

(LIU Zhichun, LI Wenjiang, ZHU Yongquan, et al. Research on Construction Time of Secondary Lining in Soft Rock of Large-Deformation Tunnel [J]. Chinese Journal of Rock Mechanics and Engineering，2008, 27(3): 580-588. in Chinese)

[4]于茂春. 铁路隧道结构计算荷载问题分析讨论 [J]. 隧道建设， 2014, 34(增): 35-40.

(YU Maochun. Discussion on Loading Issue of Railway Tunnel Structure Calculation [J]. Tunnel Construction，2014, 34(Supplement): 35-40. in Chinese)

[5]房倩, 张顶立, 王毅远，等. 高速铁路隧道初支、二衬间接触压力研究[J]. 岩石力学与工程学报， 2011, 30(增2): 3377-3385.

(FANG Qian, ZHANG Dingli, WANG Yiyuan, et al. Study of Contact Pressure between Primary Lining and Secondary Lining for Tunnels of Passenger Dedicated Lines [J]. Chinese Journal of Rock Mechanics and Engineering，2011, 30(Supplement 2): 3377-3385. in Chinese)

[6]李鹏飞, 张顶立, 赵勇，等. 大断面黄土隧道二次衬砌受力特性研究[J]. 岩石力学与工程学报， 2010, 29(8): 1690-1696.

(LI Pengfei, ZHANG Dingli, ZHAO Yong, et al. Study of Mechanical Characteristics of Secondary Lining of Large-Section Loess Tunnel [J]. Chinese Journal of Rock Mechanics and Engineering，2010, 29(8): 1690-1696. in Chinese)

[7]中华人民共和国铁道部. TB 10003—2005 铁路隧道设计规范[S]. 北京：中国铁道出版社，2005.

(Ministry of Railways of the People’s Republic of China. TB 10003—2005 Code for Design on Tunnel of Railway[S]. Beijing：China Railway Publishing House，2005.in Chinese)

[8]王哲. 平面应变状态下混凝土力学行为的三轴试验研究 [J]. 土木工程学报， 2012,45(10): 62-71.

(WANG Zhe. Tri-Axial Experimental Study of the Mechanical Behavior of Concrete in Plane Strain State [J].China Civil Engineering Journal， 2012,45(10): 62-71.in Chinese)

[9]王传志, 过镇海, 张秀琴. 二轴和三轴受压混凝土的强度试验 [J]. 土木工程学报， 1987, 20(1): 15-26.

(WANG Chuanzhi, GUO Zhenhai, ZHANG Xiuqin. Biaxial and Triaxial Compressive Strength Test of Concrete [J].China Civil Engineering Journal，1987, 20(1): 15-26.in Chinese)

[10]张素磊. 隧道衬砌结构健康诊断及技术状况评定研究[D].北京: 北京交通大学, 2012.

(ZHANG Sulei. Study on Health Diagnosis and Technical Condition Assessment for Tunnel Lining Structure [D]. Beijing: Beijing Jiaotong University, 2012. in Chinese)

[11]赵尚毅, 郑颖人, 宋雅坤，等. 地下隧道衬砌结构内力计算方法探讨[J]. 后勤工程学院学报，2007, 23(4): 29-33.

(ZHAO Shangyi, ZHENG Yingren, SONG Yakun, et al. An Analysis of the Design Method of Underground Tunnel Linings [J]. Journal of Logistical Engineering University，2007, 23(4): 29-33.in Chinese)

[12]孙克国，李术才，张庆松，等. 特长山岭隧道衬砌监测及模拟研究[J]. 岩石力学与工程学报，2007，26(增 2)：4465-4470.

(SUN Keguo，LI Shucai，ZHANG Qingsong, et al. Study on Monitoring and Simulation of Super-Long Mountain Tunnel Lining[J]. Chinese Journal of Rock Mechanics and Engineering，2007，26(Supplement 2)：4465-4470.in Chinese)

[13]童景盛, 王胜利, 敖运安. 侧压力系数研究与实践 [C]//第21届全国结构工程学术会议论文集：第Ⅰ册. 沈阳：沈阳建筑大学，2012：417-423.

(TONG Jingsheng, WANG Shengli, AO Yun’an. Research and Practice on the Lateral Pressure Coefficient [C]// Proceedings of 21st National Conference on Structural Engineering：Volume Ⅰ. Shenyang: Shenyang Jianzhu University，2012：417-423. in Chinese)

[14]关宝树. 隧道工程设计要点集[M]. 北京: 人民交通出版社, 2003: 42-57.

[15]徐干成，白洪才，郑颖人，等. 地下工程支护结构[M]. 北京：中国水利水电出版社, 2003: 68-72.

[16]陈国祥.最大水平应力对冲击矿压的作用机制及其应用研究[D].徐州：中国矿业大学, 2009.

(CHEN Guoxiang. Mechanism Research of the Maximum Horizontal Stress on Rock Burst and Its Application [D]. Xuzhou: China University of Mining and Technology,2009. in Chinese)

[17]李云安, 葛润修, 糜崇蓉，等. 岩-土-混凝土破坏准则及其强度参数估算[J]. 岩石力学与工程学报，2004, 23(5):770-776.

(LI Yun’an, GE Runxiu, MI Chongrong，et al. Failure Criteria of Rock-Soil-Concrete and Estimation of Their Strength Parameters [J]. Chinese Journal of Rock Mechanics and Engineering，2004, 23(5):770-776. in Chinese)

[18]蔡美峰, 何满潮, 刘东燕. 岩石力学与工程 [M]. 北京:科学出版社,2009: 219-228.

[19]王伟华. 钢筋混凝土梁的开裂状况对其承载力的影响研究[D]. 重庆:重庆大学, 2008.

(WANG Weihua. The Study about the Influence of Carrying Capacity on Reinforced Concrete Beam Crack Status[D]. Chongqing: Chongqing University, 2008.in Chinese)

[20]王华牢, 刘学增, 李宁, 等. 纵向裂缝隧道衬砌结构的安全评价与加固研究[J]. 岩石力学与工程学报, 2010, 29(增1): 2651-2656.

(WANG Hualao, LIU Xuezeng, LI Ning, et al. Safety Evaluation of Tunnel Lining with Longitudinal Cracks and Reinforcement Design[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Supplement 1): 2651-2656. in Chinese)

[21]黄宏伟, 刘德军, 薛亚东, 等. 基于扩展有限元的隧道衬砌裂缝开裂数值分析[J]. 岩土工程学报, 2013, 35(2): 266-275.

(HUANG Hongwei, LIU Dejun, XUE Yadong, et al. Numerical Analysis of Cracking of Tunnel Linings Based on Extended Finite Element [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 266-275. in Chinese)

[22]张顶立, 张素磊, 房倩, 等. 铁路运营隧道衬砌背后接触状态及其分析[J]. 岩石力学与工程学报, 2013, 32(2): 217-224.

(ZHANG Dingli, ZHANG Sulei, FANG Qian, et al.Study of Contact State behind Tunnel Lining in Process of Railway Operation and Its Analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(2): 217-224. in Chinese)

[23]宋瑞刚, 张顶立.“接触问题”引起的隧道病害分析[J]. 中国地质灾害与防治学报, 2004, 15(4): 69-72.

(SONG Ruigang, ZHANG Dingli. Analysis of Cause of Fracturing Failure of Tunnel Lining[J]. The Chinese Journal of Geological Hazard and Control, 2004, 15(4)：69-72.in Chinese)

[24]王立川, 周东伟, 吴剑, 等. 铁路隧道复合衬砌脱空的危害分析与防治[J]. 中国铁道科学, 2011, 32(5): 56-63.

(WANG Lichuan, ZHOU Dongwei, WU Jian, et al. The Hazard Analysis and the Treating Measures of the Voids in the Composite Linings of Railway Tunnels[J]. China Railway Science, 2011, 32(5): 56-63. in Chinese)