水逸度模型预测THF添加剂体系下气体水合物相平衡

梁海峰，朱耀剑，赵阳升，赵建忠

（1太原理工大学采煤工艺研究所，山西 太原 030024；2太原理工大学化学化工学院，山西 太原 030024）



水逸度模型预测THF添加剂体系下气体水合物相平衡

梁海峰1，2，朱耀剑2，赵阳升1，赵建忠1

（1太原理工大学采煤工艺研究所，山西 太原 030024；2太原理工大学化学化工学院，山西 太原 030024）

摘要：加入添加剂降低水合物生成压力是当前水合物法分离混合气体研究热点。本研究以水的逸度模型为基础，结合PRSV2状态方程研究了CH4、O2、N2及其混合气体水合物在纯水体系下的相平衡条件；通过UNIFAC基团贡献法对添加剂四氢呋喃（THF）水溶液进行基团划分，计算该体系下液相各组分的活度，理论研究了添加剂THF对气体水合物相平衡条件的影响；结果表明在相应的温度范围内，与其他模型相比，在纯水体系下该模型预测精度较高，在THF水溶液体系下该模型对单组分和双组分气体的预测精度平均相对误差在7%左右，随着THF浓度增加，气体水合物相平衡压力的降低幅度减小；当THF摩尔分数达到6%时，对气体水合物相平衡影响达到最大。相关研究结果为混合气体的大规模工业提纯分离提供了理论基础。

关键词：模型；水合物；相平衡；活度系数；四氢呋喃；UNIFAC基团贡献法

项目。

第一作者及联系人：梁海峰（1980—），男，博士，讲师，主要从事多孔介质内传热传质及水合物开采研究。E-mail lianghaifeng@tyut.edu.cn。

气体水合物是小分子气体与水在一定的温度、压力条件下（通常为低温、高压条件）生成的非化学计量半笼型晶体，水分子构成笼型结构，气体分子填充在笼型中，两者之间通过范德华力保持稳定。根据笼型结构的不同，气体水合物结构分为Ⅰ、Ⅱ和H型。利用不同气体之间生成水合物的温度、压力条件差异来实现混合气体的分离是当前气体分离技术的研究热点之一。

目前，国内外学者对水合物法分离混合气体进行了大量的理论与实验研究，并取得了较大的进展。HAPPEL等[1]首先在1994年利用新的分离装置通过水合物法分离氮气和甲烷；马昌峰等[2]等对甲烷和氢气、二氧化碳和氢气分别进行了水合物法分离试验，结果表明采用水合物法提纯氢气效果良好；YAMAMOTO[3]、KANG[4]和孙强[5]等分别通过水合物法进行了混合气体的分离实验，都得到了较为理想的结果。而通过加入添加剂来降低水合物生成平衡条件也是许多学者研究的热点[6-11]，ZHONG 等[12-13]分别研究了四丁基溴化铵（TBAB）和环戊烷/环己烷存在下低浓度煤层气的水合物相平衡条件，结果表明同纯水体系相比，混合气体水合物相平衡条件向高温低压区域转变，并且水合物相中包含的甲烷分数增加为约0.5；孙登林等[14]研究了蒙脱石（MMT）对低浓度瓦斯水合分离效率的影响，加入MMT后甲烷提纯率可提高30%左右；吴强等[15]研究发现，SDS-高岭土条件下甲烷的提纯率可提高至58.41%。在理论研究方面，更多学者研究通过理论模型来研究在纯水体系下的水合物相平衡条件。1959年，VAN DER WAALS和PLATTEEUW[16]建立了基于统计热力学的模型（vdW-P模型），成功预测了甲烷水合物的相平衡条件，随后PARRISH[17]、ROBINSON[18]、JOHN[19]、DU[20]、高伟[21]、李小森[22]等对vdW-P模型进行修正的基础上，取得了更好的预测结果。我国学者CHEN等[23-26]提出了一个双步骤水合物成核动力学机理模型（Chen-Guo模型），并成功预测了多种单组分及双组分混合气体的水合物相平衡条件。2000年，KLAUDA等[27-28]提出了基于各相中水的逸度相等的模型，对N2、CO2、CH4等单组分进行了相平衡研究，取得了更好的预测效果。综上，目前关于混合气体在促进剂条件下水合物相平衡的研究大多数仅限于实验，在理论方面的研究仍然侧重在单组分及双组分气体在纯水体系中的相平衡研究，尤其对于对水合物生成影响较大的添加剂四氢呋喃（THF）相平衡理论研究较少。本研究以水的逸度模型为基础，结合PRSV2状态方程研究了混合气体水合物在纯水体系下的相平衡条件；通过UNIFAC基团贡献法对添加剂THF水溶液进行基团划分，计算该体系下液相各组分的活度，理论研究了添加剂THF对水合物相平衡条件的影响。

1 水逸度模型

水逸度模型，即在相平衡状态下水合物相中水的逸度与液相或冰相中水的逸度相等，见式(1)。

式中，f为逸度，Pa；T为温度，K；P为压力，Pa；上角标H、π分别代表水合物相和水或冰相，下角标w代表水。

1.1 水合物相中水的逸度计算

水合物相中水的逸度计算公式如式(2)所示。

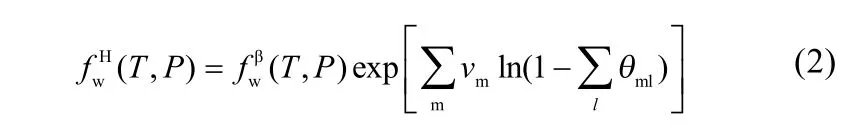
式中，vm为空水合物晶格中每个水分子所拥有的m型孔穴数，对于Ⅰ型水合物，大、小孔穴的值分别为2/46、6/46；对于Ⅱ型水合物，大、小孔穴的值分别为16/136、8/136；上角标β为空水合物晶格；θml为客体分子l在m型孔穴的占有率，其表达式如式(3)所示。

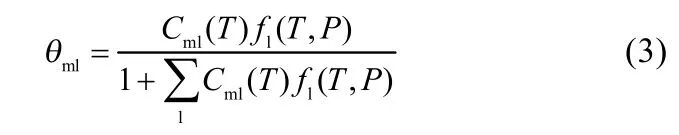
式中，Cml(T)为Langmuir常数，将采用Du-Guo模型[20]来计算；下角标l表示气体，fwβ为空水合物的逸度，其表达式如式(4)所示。

气相逸度采用修正的PR方程Peng-Robinson-Stryjek-Vera状态方程[29]（PRSV2 EOS），如式(5)。

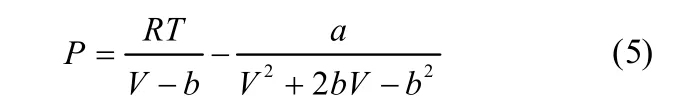
式中，R是气体常数；T为温度，K；V为摩尔体积，mol/m3；a和b分别表示为反应分子间吸引力和体积的参数，见式(6)～式(9)。

式(6)～式(9)中，TC为临界温度，K；Pc为临界压力，MPa；ω为偏心因子；k1、k2和k3分别为经验常数，相关数值如表1所示。

表1 PRSV2方程中参数值

对于混合气体，采用Reid建议的混合规则，见式(10)、式(11)。

式(10)、式(11)中，下角标i、j分别为气体组分类别；m为混合气体。

对于液相中添加剂存在时，本文对采用的逸度模型进行稍微修正，即假定气体小分子（CH4、N2、O2）同添加剂分子（四氢呋喃）形成Ⅱ型水合物，其中添加剂分子完全占据大孔，而气体小分子只进入小孔。相应的水合物相水的逸度公式为式(12)～式(14)所示。

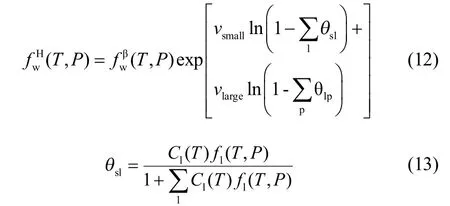
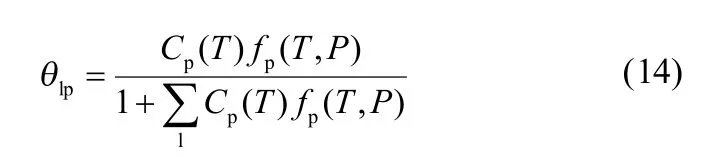
式(12)～(14)中，vsmall和vlarge分别为水合物晶格中每个水分子所占有的小孔和大孔数；θsl为气体小分子在小孔穴的占有率；θlp为添加剂分子在大孔穴的占有率；Cl、Cp为Langmuir常数；下角标p表示添加剂。添加剂逸度计算公式如式(15)所示。

式中，x为添加剂在液相中的摩尔分数；γ为活度系数；下角标p表示添加剂。

1.2 冰及液相中水的逸度

冰及液相中水的逸度表达式分别如式(16)、式(17)所示。

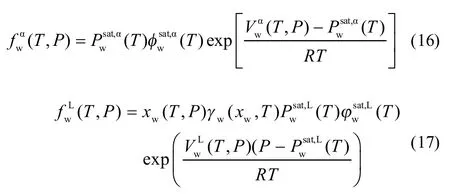
采用KRICHEVSKY等[30]提出的溶解度方程计算水合物存在下气体的溶解度，简称K-K方程，其公式如式(18)所示。

式中，sl为气体组分l的溶解度；HlW为气体组分l的亨利系数；Vl∞为无限稀释下气体组分l的摩尔体积，mol/m3。其中无限稀释下气体组分l的摩尔体积和亨利系数的获得是求解气体溶解度的关键，采用Van’t Hoff方程[31]计算各种气体的亨利系数。具体公式如式(19)所示。

表2 K-K方程中参数值

2 UNIFAC基团贡献法

UNIFAC基团贡献法是把溶液看成是由各个基团混合而成的，即采用有限量的基团数取代各种化合物及其组成的溶液，混合物各组分的活度系数可由组成混合物分子各基团的基团参数及相互作用参数得到。UNIFAC法是将活度系数lniγ表示为组合部分和剩余部分之和，见式(20)。式中，为考虑分子大小和形状对活度系数的贡献，其表达式如式(21)所示。

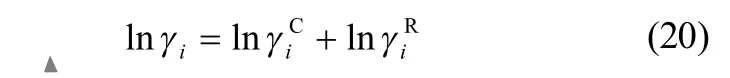
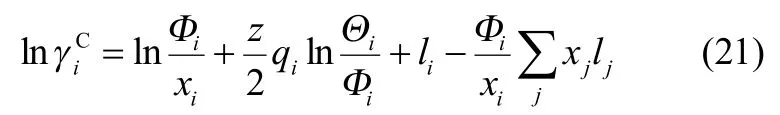
式中，Z为配位数，取值10；i、j代表组分；xi、xj分别为组分i、j的摩尔分数；Φi为组分i的体积分数；Θi为组分i的面积分数；qi为组分i的面积参数。

剩余部分活度系数表达式如式(22)所示。

表3和表4分别给出了UNIFAC模型中部分基团参数及基团之间的交互作用参数[32-34]。

3 结果与讨论

3.1 单组分气体

为了验证模型的准确性，对单组分气体N2、O2和CH4水合物进行了模型预测，并与实验值[35-36]及vdW-P模型、Chen-Guo模型预测结果[37]进行对比，如图1所示。从图1中可以看出，CH4和N2水合物实验值与模型预测值非常接近，且吻合良好，对O2而言，温度较低时误差较大，而随着温度的升高，实验值与模型预测值较为吻合，这表明水逸度模型可以较好地预测单组分气体的水合物相平衡条件。

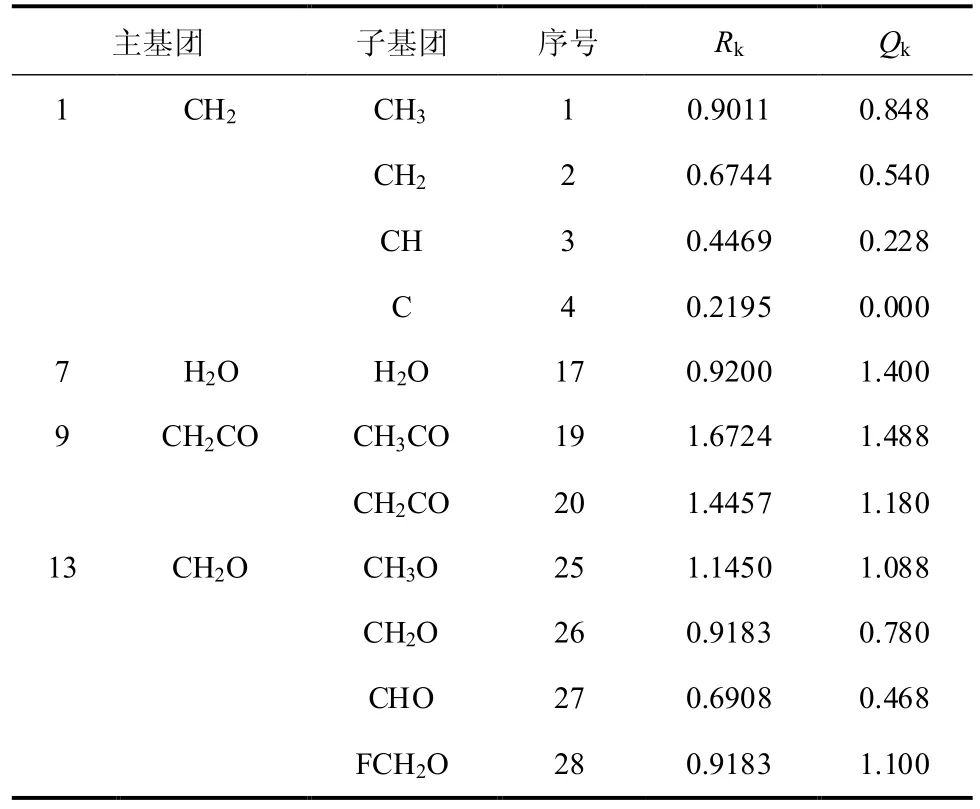
表3 UNIFAC模型的相关参数

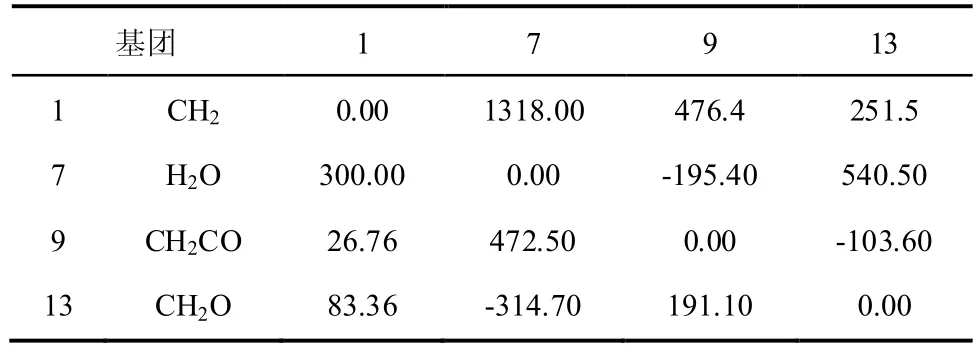
表4 基团之间的交互参数

同时，图1比较了3种模型对单组分气体水合物相平衡条件的预测精度。从图1中可以看出，对于CH4气体水合物，3种模型预测精度较为接近；对于N2水合物，在温度较低时逸度模型预测精度较差，随着温度升高，预测结果较为准确；对于O2水合物，在相应温度条件下逸度模型预测精度较好。

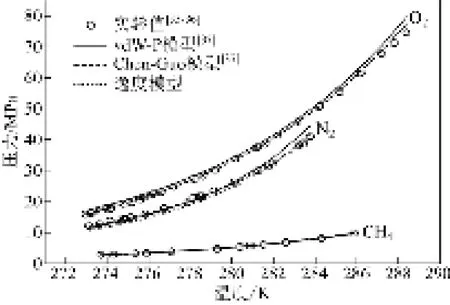
图1 不同模型条件下N2、O2和CH4气体水合物生成相平衡曲线

图2 CH4、N2和O2气体在THF存在下水合物生成相平衡曲线

图2 所示为单组分气体CH4、N2和O2水合物在不同THF摩尔分数下模型预测值与实验数据对比示意图。从图2中可以看出，模型预测值同实验参考数据较为吻合。同时，在添加THF条件下，各气体水合物生成压力大大下降，表明添加THF可以极大地降低气体水合物生成压力。

3.2 双组分气体

双组分混合气体水合物相平衡研究是目前许多学者研究的重点，本研究也就此进行了相关研究。图3所示为79%N2-21%O2在纯水及THF摩尔分数为5%条件下模型预测值与实验数据[36]对比图。从图3中可见，预测值与实验值吻合良好，且随着温度升高，压力呈指数上升，而在THF条件下，在较高温度下相平衡曲线趋缓，水合物相平衡压力下降幅度更大。

3.3 相对误差分析

为了更直观地了解模型的预测精度，表5给出了各组分在不同摩尔分数THF存在下的模型预测值同实验数值之间的平均相对误差。从表5中可以看出，在相应的温度范围内，单组分和双组分气体水合物的预测精度平均相对误差在7%左右，效果相对较好。

图3 (79%N2-21%O2)+5%THF体系水合物相平衡曲线

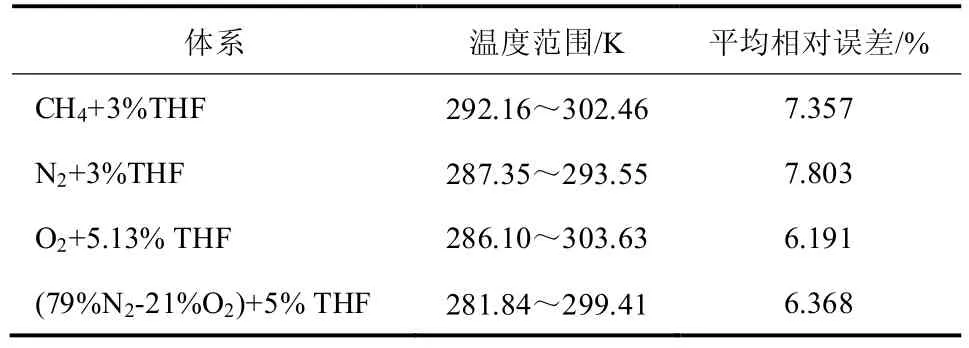
表5 THF存在下不同组分的平均相对误差

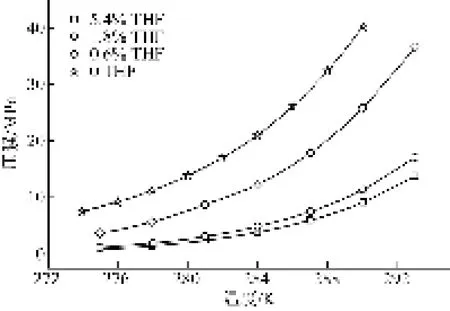
图4 不同体系下低浓度煤层气水合物生成相平衡曲线

3.4 煤层气水合物相平衡预测

在上述研究基础上，对不同摩尔分数THF溶液条件下，低浓度煤层气（26%CH4-60%N2-14%O2）水合物相平衡生成条件进行预测并比较分析，以作理论参考。

图4所示为不同THF摩尔分数条件下低浓度煤层气水合物相平衡曲线图。通过图4可以看到，无论溶液中THF存在与否，低浓度煤层气水合物相平衡生成压力都随温度升高而升高；THF的存在显著降低了水合物的生成压力；为了更形象直观地看出THF的降低效果，选取温度为284K时，THF摩尔分数为5.4%、1.8%以及0.6%溶液同纯水体系相比，相应的煤层气水合物相平衡压力降低幅度分别为81.74%、76.89%、41.71%；随着溶液中THF含量增加，低浓度煤层气水合物相平衡压力的降低幅度逐渐减小，这与相关学者研究[9-10]THF摩尔分数为6%时对气体水合物相平衡条件影响最大相一致。

4 结 论

在本研究中，以水的逸度模型为基础，结合PRSV2状态方程研究了单组分气体N2、O2和CH4水合物在纯水体系下的相平衡条件；通过UNIFAC基团贡献法对添加剂THF水溶液进行基团划分，计算该体系下液相各组分的活度，理论研究了添加剂THF对水合物相平衡条件的影响，得出了以下结论。

（1）所建立的水逸度模型+PSRV2状态方程能够有效的预测纯水体系下单组分及混合气体的水合物相平衡条件。

（2）结合UNIFAC基团贡献法，采用上述模型能够很好的预测促进剂THF条件下单组分及混合气体的水合物相平衡条件，为进一步优化添加剂选择提供了理论参考。

（3）通过研究不同THF摩尔分数对气体水合物相平衡的影响，发现THF的存在可以显著降低气体水合物相平衡生成压力；一定温度下，随着溶液中THF含量的不断增加，低浓度煤层气水合物相平衡生成压力降低幅度逐渐减小。

参 考 文 献

[1] HAPPEL J，HNATOW M A，MEYER H. The study of separation of nitrogen from methane by hydrate formation using a novel apparatus[J]. Annals of the New York Academy of Sciences，1994，715（1）：412-424.

[2] 马昌峰，王峰，孙长宇，等.水合物氢气分离技术及相关动力学研究[J].石油大学学报（自然科学版），2002，26（2）：76-78.

[3] YAMAMOTO Y，KOMAI T，KAWAMURA T，et al. Studies on separation and purification of guest component[C]//Proc.4th International Conference on Gas Hydrates，Yokohama，Japan，2002：428-432. [4] KANG S P，LEE H. Recovery of CO2from flue gas using gas hydrate thermodynamic verification through phase equilibrium measurements[J]. Environmental & Science Technology，2000，34 （20）：4397-4400.

[5] 孙强，刘爱贤，郭绪强. 水合物法分离合成气实验研究[J].高校化学工程学报，2010，24（5）：739-744.

[6] 吕秋楠，李小森，徐纯刚，等.低浓度煤层气分离提纯的研究进展[J].化工进展，2013，32（6）：1267-1272.

[7] MAINUSCH S，PETERS C J，SWAAN A J，et al. Experimental determination and modeling of methane hydrate in mixture of acetone and water[J]. Journal of Chemical and Engineering Data，1997，42 （5）：948-950.

[8] HEUVEL M M，PETERS C J，ARONS J S. Influence of waterinsoluble organic components on the gas hydrate equilibrium conditions of methane[J]. Fluid Phase Equilibrium，2000，172（1）：73-91.

[9] SUN Q，GUO X Q，LIU A X，et al. Experiment on the separation of air-mixed coal bed methane in THF solution by hydrate formation[J]. Energy & Fuels，2012，26（7）：4507-4513.

[10] SUN Qiang，CHEN Guangyin，GUO Xuqiang，et al. Experiments on the continuous separation of gas mixtures via dissolution and hydrate formation in the presence of THF[J]. Fluid Phase Equilibria，2014，361（1）：250-256.

[11] FAKHARIAN H，GANJI H，NADERI F A，et al. Potato starch as methane hydrate promoter[J]. Fuel，2012，94（1）：356-360.

[12] ZHONG D L，ENGLEZOS P. Methane separation from coal mine methane gas by tetra-n-butyl ammonium bromide semiclathrate hydrate formation[J]. Energy & Fuels，2012，26（4）：2098-2106.

[13] ZHONG D L，DING K，YANG C，et al. Phase equilibria of clathrate hydrates formed with CH4+N2+O2in the presence of cyclopentane or cyclohexane[J]. Journal of Chemical and Engineering Data，2012，51 （12）：3751-3755.

[14] 孙登林，张强，张保勇，等.蒙脱石对低浓度瓦斯水合分离效率的影响[J].黑龙江科技学院学报，2012，22（4）：372-376.

[15] 吴强，朱玉梅，张保勇.低浓度瓦斯气体水合分离过程中十二烷基硫酸钠和高岭土的影响[J].化工学报，2009，60（5）：1193-1198.

[16] VAN DER WAALS J A，PLATTEEUW J C. Clathrate solutions[J]. Advances in Chemical Physics，1959，2（1）：2-57.

[17] PARRISH W R，PRAUSNITZ J M. Dissociation pressures of gas hydrates formed by gas mixtures[J]. Industrial & Engineering Chemistry，1972，11（1）：27-35.

[18] NG H J，ROBINSON D B. The measurement and prediction of hydrate formation in liquid hydrocarbon-water system[J]. Industrial & Engineering Chemistry Fundamentals，1976，15（4）：293-297.

[19] JOHN V T，PAPADOPOULOS K D，HOLDER G D. A generalized model for predicting equilibrium conditions for gas hydrates[J]. AIChE Journal，1985，31（2）：252-259.

[20] DU Y H，GUO T M. Prediction of hydrate formation for systems containing methanol[J]. Chemical Engineering Science，1990，45（4）：893-900.

[21] 高伟.天然气水合物相平衡及其表面张力影响研究[D].南京：东南大学，2005.

[22] 李小森，吴慧杰，冯自平，等.利用统计缔合流体理论状态方程预测混合气体水合物的平衡形成条件[J]. 化学学报，2007，65（1）：59-66.

[23] CHEN G J，GUO T M. A new approach to gas hydrate modeling[J]. Chemical Engineering Journal，1998，71（2）：145-151.

[24] 陈光进，马庆兰，郭天明.气体水合物生成机理和热力学模型的建立[J]. 化工学报，2000，51（5）：626.

[25] SUN C Y，MA C F，CHEN G J，et al. Experimental and simulation of single equilibrium stage separation of （methane+hydrogen） mixtures via forming hydrate[J]. Fluid Phase Equilibria，2007，261（1/2）：85-91. [26] LIAO Zhixin，GUO Xuqiang，ZHAO Yanyan，et al. Experimental and modeling study on phase equilibria of semiclathrate hydrates of tetra-n-butyl ammonium bromide + CH4，CO2，N2，or gas mixtures[J]. Industrial & Engineering Chemistry Research，2013，52（51）：18440-18446.

[27] KLAUDA J B，SANDLER S I. A fugacity model for gas hydrate phase equilibria[J]. Industrial & Engineering Chemistry Research，2000，39（9）：3377-3386.

[28] MORADI G，KHOSRAVANI E. Modeling of hydrate formation conditions for CH4，C2H6，C3H8，N2，CO2and their mixtures using the PRSV2 equation of state and obtaining the Kihara potential parameters for these components[J]. Fluid Phase Equilibria，2013，338（1）：179-187.

[29] PENG D Y，ROBINSON D B. A new two-constant equation of state[J]. Industrial & Engineering Chemistry Fundamentals，1976，15（1）：58-64.

[30] KRICHEVSKY I R，KASARNOVSKY J S. Thermo dynamical calculations of solubilities of nitrogen and hydrogen in water at high pressures[J]. Journal of the American Chemical Society，1935，57 （11）：2168-2171.

[31] JOSEPH C M，RUBLN B，MOTHY R R，et al. Partial molar volumes of gases at infinite dilution in water at 298.15K[J]. Journal of Chemical and Engineering Data，1982，27（1）：22-24.

[32] 郭天民.多元汽-液平衡和精馏[M]. 北京：石油工业出版社，2002.

[33] FREDENSLUND A，JONES R L，PRAUSNITZ J M. Group-contribution estimation of activity coefficients in no ideal liquid mixtures[J]. AIChE Journal，1975，21（6）：1086-1099.

[34] POLING B E，PRAUSNITZ J M，O’CONNELL J. The properties of gases and liquid[M]. 5th ed. New York：McGraw-Hill，2001.

[35] SEO Y T，KANG S P，LEE H. Experimental determination and thermodynamic modeling of methane and nitrogen hydrates in the presence of THF，propylene oxide，1,4-dioxane and acetone[J]. Fluid Phase Equilibria，2001，189（1/2）：99-110.

[36] YANG H J，FAN S S，LANG X M，et al. Phase equilibria of mixed gas hydrates of oxygen+tetrahydrofuran，nitrogen+tetrahydrofuran，and air+tetrahydrofuran[J]. Journal of Chemical and Engineering Data，2011，56（11）：4152-4156.

[37] 朱耀剑. 水合物法分离低浓度煤层气热力学模型预测[D]. 太原：太原理工大学，2014.

研究开发

Phase equilibrium study of gas mixtures hydrate formation with additives THF based on water fugacity model

LIANG Haifeng1，2，ZHU Yaojian2，ZHAO Yangsheng1，ZHAO Jianzhong1

（1Mining Technology Institute，Taiyuan University of Technology，Taiyuan 030024，Shanxi，China；2College of Chemistry and Chemical Engineering，Taiyuan University of Technology，Taiyuan 030024，Shanxi，China）

Abstract：Gas hydrates have absorbed more and more attentions as a potential medium for gas separation. The additive promoters can reduce the hydrate equilibrium pressure at a given temperature. In this paper，we had mainly conducted on phase equilibrium of CH4、O2、N2and corresponding gas mixtures hydrate based on the water fugacity model integrated with the gas state equations of PRSV2. Furthermore，the groups of additive-aqueous solution were divided based on UNIFAC group contribution method to calculate activity of each composition in aqueous phase，and the effects of additives on phase equilibrium pressure of aforementioned gas mixtures hydrate were studied. The results showed that the water fugacity model is more accurate compared with other models in pure water system. Under the condition of tetrahydrofuran (THF) aqueous solution system，the water fugacity model prediction accuracy is about 7% for single or double-component gas hydrate. With the increase of THF concentration，the scale of the equilibrium pressure depression is reduced. When the THF aqueous solution concentration reaches 6% mole fraction，the phase equilibrium pressure of gas hydrate reaches the minimum.

Key words：model；hydrate；phase equilibria；activity coefficient；THF additives；UNIFAC group contribution method

基金项目：国家自然科学基金青年基金（51106104）、山西省自然科学基金青年基金（20120210022-5）及国家自然科学基金（51074111）

收稿日期：2015-09-02；修改稿日期：2015-10-23。

DOI：10.16085/j.issn.1000-6613.2016.03.007

中图分类号：TQ 028.8

文献标志码：A

文章编号：1000–6613（2016）03–0700–06