基于广义逆矩阵的多层径向基函数网络遗传算法
2016-03-28盛国敏
盛国敏,庄 健
(安徽工业大学商学院,安徽马鞍山243032)
基于广义逆矩阵的多层径向基函数网络遗传算法
盛国敏,庄 健
(安徽工业大学商学院,安徽马鞍山243032)
为了解决以往正则最小二乘法求权重向量时遇到的矩阵接近奇异而无法求逆的问题,采用广义逆矩阵的方法求多层径向基函数网络中各层的权重向量,并将这种方法引至多层径向基函数网络的遗传算法中。采用实函数逼近,混沌时间序列建模与预测等仿真实验对算法进行验证。结果表明,采用广义逆矩阵的方法要比正则最小二乘法在逼近精度上高1至2个数量级。
多层径向基函数网络;遗传算法;广义逆矩阵;实函数逼近;混沌时间序列
聚类算法经历了从单层径向基函数网络[1]向多层径向基函数(RBF)网络[2],并由最初的采用多层径向基函数网络的聚类法[2-4]发展到了采用多层径向基函数网络的遗传算法[5],进一步发展为复合多层RBF网络[6]的发展历程,仿真实验表明,多层RBF网络逼近实函数的能力很强,将其用于混沌时间序列[7]的建模与预测中,可取得良好的效果,将其用于偏微分方程的无网格法[8-9]和求解期权定价值[10-12]可获得高精度的数值解。然而,多层RBF网络的诸算法均存在数值计算问题,即逆矩阵的计算遇到矩阵接近奇异而难以求逆的问题。这使得网络的学习速度变慢,权向量误差大,逼近实数精度的提高受到限制。为解决问题,本文尝试使用广义逆矩阵[13]代替普通逆矩阵求最小二乘解,并将其引入多层RBF网络的遗传算法。
1 多层径向基函数网络原理
单层RBF网络学习速度快,具有一定的实函数逼近能力,但是其拟合函数的精度有限。多层RBF网络的提出进一步提高RBF网络的实函数逼近能力,基本思想:用第2层RBF网络去拟合第1层网络的拟合残差函数,然后再用第3层网络RBF网络去拟合第2层网络的拟合残差函数,如此进行下去,后一层网络拟合前一层的拟合误差,就得到一个高精度的多层径向函数网络。
设第1层RBF网络为
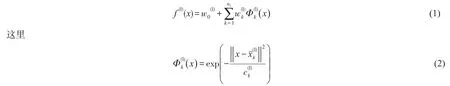

取最小值,式中w1为权重的向量表达形式。记

这是第1层网络在xi处的输出值与期望值yi的拟合残差。第2层RBF网络为
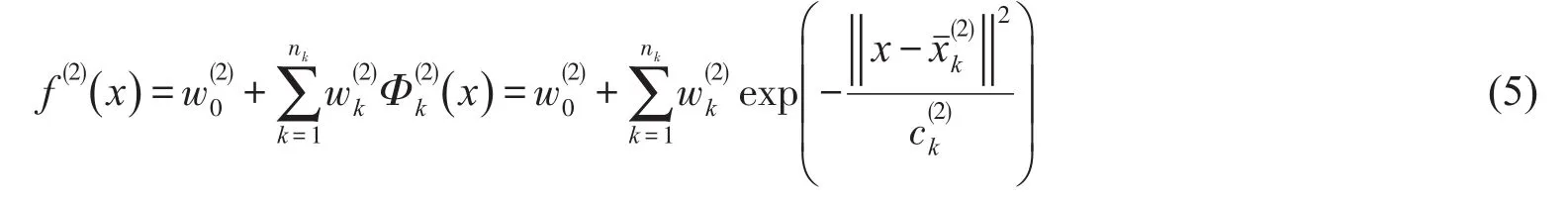
式中各参数的含义和第1层类同。核函数中心和宽度系数的取值也使第2层的广义交叉率G最小,权重则使

最小,其中w2为权重的向量表达形式。于是可得一个更精确的模型

如此进行下去,用后一层径向基函数网络去拟合前一层网络的拟合残差,便得到一个多层RBF网络

根据适当的判别准则,可以决定增加到几层最为适合。
2 多层径向基函数网络的遗传算法
采用自适应遗传算法训练多层RBF网络,具体如下。
1)对RBF网络的进行遗传编码 采用实数编码的方法,设第k层网络核函数的个数为nk,每个核函数的输入维数为m。此时,每个个体用(m+1)×nk维的向量来表示,向量的前m×nk个分量表示RBF网络的中心,后nk个分量表示中心所对应的宽度系数。
2)选取适应度函数 为了既能得到最大限度的高逼近精度,又不出现过拟合现象,每个个体的适应度函数可以选取为RBF网络的广义交叉率的倒数,即对第i个个体,其适应度为

3)选择操作 首先根据每一代种群的个体的适应度的大小,得到最优个体和最劣个体,用最优个体替换最劣个体,直接复制给下一代,不参加交叉和变异的过程。剩下的种群个体通过赌轮盘法进行筛选,然后进行交叉和变异操作。
4)交叉和变异 记交叉概率为pc,变异概率pm,其自适应计算方法如下:

其中:a=0.9;b=0.1,c=0.6,d=0.001;fmax表示群体中最大适应度值;favg表示每一代群体的平均适应度值;f′表示要交叉的两个个体中较大的适应度值;f表示要变异个体的适应度值。
5)权重的计算 采用正则最小二乘法,


这里,λ为求权重时的正则最小二乘法的参数。当λ=0时,w即为普通最小二乘解。对第1层网络对第i层网络对第k层网络
6)RBF网络层数的确定 设第m层的广义交叉率为第m+1层则为如果

则停止加层,网络层数为m。
3 广义逆矩阵法在多层径向基函数网络遗传算法中应用
在大多数情况下,由于式(12)中BTB接近奇异,使得计算逆矩阵很困难,勉强得到的数值解精度很差,从而使整个网络的精度大大下降,为解决这一问题,采用广义逆矩阵求最小二乘法[8]。设A为m×n类数矩阵,A的广义逆矩阵[9]X满足下面4个条件,即,

X常记为A+。于是,线性模型

的最小二乘估计β^为

将式(20)用于RBF网络,并采用最小二乘法,得到

这里B由式(13)给出,再给出本文使用的广义逆矩阵的一个迭代算法,取初始值

其中λ1(ATA)为ATA的最大特征值,迭代公式

4 仿真实验
遗传算法的参数为:进化的代数为100,种群的规模为200,学习参数为a=0.9,b=0.1,c=0.6,d=0.001。根据G决定层数确定层数,控制参数为0.05。
4.1 实验一
考虑函数
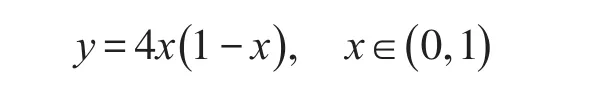
随机生成400个在(0,1)上服从均匀分布的样本。200个样本用于训练,其余200个用于检验。网络构造为:第1层RBF网络取10个径向基函数,第2层取20个,第3层以后取30个。
表1给出了预测结果以及采用基于正则最小二乘法的遗传算法训练得到的网络的学习误差和预测误差。由表1可见基于广义逆矩阵的遗传算法的精度要比基于正则最小二乘法的遗传算法高约1个数量级。

表1 多层RBF网络的训练与预测结果Tab.1 Training and prediction results of multilayer RBF network
4.2 实验二
考虑函数
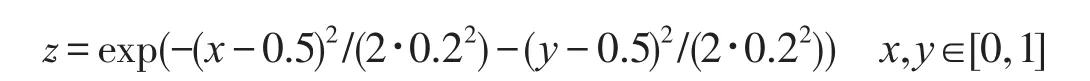
生成3 200个服从在(0,1)上均匀分布的样本,其中1 600个作为训练用样本,其余1 600个用于检验。网络构造为:第1层RBF网络取40个径向基函数,第2层以后取80个。
表2给出了预测结果以及采用基于正则最小二乘法遗传算法训练得到的网络学习误差和预测误差。由表2可见基于广义逆矩阵的遗传算法精度要比基于正则最小二乘法的遗传算法高约2个数量级。

表2 多层RBF网络的训练与预测结果Tab.2 Training and prediction results of multilayer RBF network
4.2 实验三
考虑Logistic模型

其中R是参数,取R=3.7。取初始值x0=0.27。共产生700个时间序列样本,前600个用于学习,后100个用于检验预测效果。前700个中,前650个用于学习,后50个用于计算可预测步长。网络构造为:第1层RBF网络取80个径向基函数,第2层以后取120个,嵌入维数取p=7。
表3给出了一步预测结果以及采用基于正则最小二乘法遗传算法训练而得到的网络学习误差和一步预测误差。由表3可见基于广义逆矩阵的遗传算法精度要比基于正则最小二乘法的遗传算法高约1个数量级。

表3 多层RBF网络的训练和一步预测结果Tab.3 Training and one step prediction results of multilayer RBF network
表4给出了多步预测的可预测步长和预测精度以及基于正则最小二乘法遗传算法训练而得到的网络可预测步长和预测精度。可见在同样的误差容许范围内,基于广义逆矩阵的遗传算法的可预测步长要比基于正则最小二乘法的遗传算法长许多。

表4 多层RBF网络的多步预测结果Tab.4 Multi-step prediction results of multilayer RBF network
4.4 实验四
考虑Mackey_Glass混沌时间序列,它由如下Mackey Glass方程所产生

τ为时滞参数。这里取a=0.2,b=0.1,c=10,τ=30,x0=1.2。产生800个时间序列的样本,前700个作为学习用样本,后100个作为预测用样本。
在Mackey Glass方程中有一个线性项,由于高斯函数为峰状函数,因此RBF网络在拟合线性项的时候精度不高,如果仅仅使用高斯函数,模型的逼近精度不高,预测效果不好。为此在第1层网络中加上了线性项,其具体形式为

网络构造为第1层RBF网络取80个径向基函数,第2层以后取120个,嵌入维数取p=6。学习用样本的前650个用于训练,后50个用于计算可预测步长。
表5给出了一步预测结果及采用基于正则最小二乘法遗传算法训练而得到的网络学习精度和一步预测精度。由表5可见基于广义逆矩阵遗传算法的精度要比基于正则最小二乘法遗传算法高约1到2个数量级。

表5 多层RBF网络的训练和一步预测结果Tab.5 Training and one step prediction results of multilayer RBF network
表6给出了多步预测的可预测步长和预测精度,以及由基于正则最小二乘法遗传算法训练而得到的网络可预测步长和预测精度。可见在同样的误差容许范围内,基于广义逆矩阵的遗传算法的可预测步长要比基于正则最小二乘法的遗传算法长许多。

表6 多层RBF网络的多步预测结果Tab.6 Multi-step prediction results of multilayer RBF network
5 结 论
用广义逆矩阵计算多层RBF网络的每层权连接,仿真实验表明,采用广义逆矩阵遗传算法得到的权重其精度大大提高,网络的后一层能更好地拟合前一层的拟合误差,整个网络的实函数逼近能力就这样大大提高。将这个方法用于混沌时间序列的建模与预测得到了良好的效果。
[1]MOODYJ,DARKEN C.Fast learning in networks of locally-tuned processing units[J].Neural Computation,1989,1(2):281-294.
[2]ZHANG J,JIANG H F,WU R L.Multi layer RBF network for real functions approximation and nonlinear regression[C/CD]// Scientific Research Publishing.Proceedings of 2011 International Symposium on Statistics&Management Science.Chongqing: Scientific Research Publishing,2011.
[3]吴瑞柳.多层径向基函数网络的聚类学习方法及应用[D].马鞍山:安徽工业大学,2011.
[4]李建.多层径向基函数网格的算法改进及其应用[D].马鞍山:安徽工业大学,2013.
[5]盛飞.多层RBF网络的自适应遗传算法及其在实函数逼近中的应用[J].安徽工业大学学报(自然科学版),2013,30(2):192-196.
[6]徐光鲁.复合多层径向基函数网络及其在偏微分方程中的应用[J].安徽工业大学学报(自然科学版),2015,32(1):76-80.
[7]余健,郭平.基于RBF网络的金融时间序列预测[J].湖南工程学院学报(自然科学版),2007,17(4):44-48.
[8]LIU G R,GU YT.无网格法理论及程序设计[M].王建明,周学军,译.济南:山东大学出版社,2007:259-264.
[9]张雄,刘岩.无网格法[M].北京:清华大学出版社,2004:95-175.
[10]侯木舟,周耀琼.二叉树期权定价方法的一种新推广[J].数学理论与应用,2006,26(3):111-115.
[11]牟旷凝.蒙特卡洛方法和拟蒙特卡洛方法在期权定价中应用的比较研究[J].科学技术与工程,2010,10(8):1925-1929.
[12]蹇明,宜娜,张春晓.期权定价模型的五点式混合差分方法[J].经济数学,2011,28(4):66-70.
[13]王宋桂,杨振海.广义逆矩阵及其应用[M].北京:北京工业大学出版社,1996.
责任编辑:丁吉海
GeneticAlgorithm for Multilayer Radial Basis Function Networks Based on Generalized Inverse Matrix
SHENG Guomin,ZHUANG Jian
(School of Business,Anhui University of Technology,Ma'anshan 243032,China)
In order to solve the problem that maxtrice are nearly singular when using regular least squares method, a method of generalized inverse matrix was employed to obtain the weight vectors of each layer in the multilayer radial basis function network,which was introduced to the genetic algorithm for training multilayer radial basis function networks.By using real function approximation,chaotic time series modeling and forecasting simulation experiments,the algorithm was verified.The results show that the generalized inverse matrix method is much more better than regular least squares method on the approximation precision,which can be up to a 1 to 2 orders of magnitude.
multilayer radial basis function networks;genetic algorithm;generalized inverse matrix;real function approximation;chaos sequence
TP 389.1
:A
10.3969/j.issn.1671-7872.2016.04.015
1671-7872(2016)04-0390-06
2015-07-29
盛国敏(1989-),男,安徽天长人,硕士,助教,研究方向为机器学习。
庄健(1957-),男,上海市人,博士,研究员,研究方向为机器学习。
