一类Logistic时变收获模型的渐近分析
2016-03-28蒋小惠陈松林
周 倩,蒋小惠,陈松林
(1.河海大学文天学院基础部,安徽马鞍山243031;安徽工业大学数理科学与工程学院,安徽马鞍山243032)
一类Logistic时变收获模型的渐近分析
周 倩1,蒋小惠2,陈松林2
(1.河海大学文天学院基础部,安徽马鞍山243031;安徽工业大学数理科学与工程学院,安徽马鞍山243032)
研究一类含小参数的Logistic时变收获模型问题。采用匹配法构造其近似解,通过上下解法证明近似解的一致有效性,并给出近似解与精确解之间的误差估计。运用非线性多重尺度法,获得在更长时间范围内的形式渐近解。
Logistic收获模型;近似解;匹配法;多重尺度法
Logistic模型[1-3]由于其形式简单、参数生物意义明确、动态行为清晰等特性,使其在生态学、生物资源管理、细胞和分子生物学、生命科学等众多领域得到了广泛的应用。该模型描述种群的S型增长[4],可表征种群的数量动态。
Logistic时变收获模型可表示为

其中:r为内禀增长率;k为环境容纳量;h为收获率。当r,k,h为正常数时,即Schaefer模型。实际中,r,k,h往往随时间缓慢变化,式(1)可表示成这里ε为正的小参数,且满足此即Bernoulli方程。在绝大多数情况下,式(2)的显式解析解较难获得或表达式复杂,从而其渐近性态不易获得。本文先通过匹配法,得出其近似解,并给出其与精确解之间的误差估计和渐近性态分析。再利用多重尺度法,构造两个不同的时间尺度,获得在更长时间范围内的渐近解。

1 时变模型的匹配法
若λ=εt作为慢尺度,则系统(2)可被转换成如下奇异摄动问题[5-6]

此时,系统(2),(3)分别称为快、慢系统。
为使用匹配法,先来求快系统的首次近似,即令式(2)中ε=0,得

再求慢系统(3)的首次近似得

由式(4)和式(5)可得

由Prandtl匹配原理可得式(2)的首次形式合成近似解[7]为

下一步证明当ε足够小时,近似解(6)在任何有界区间上是一致有效的。
引理[8]设α,β∈C1[a,b],α(t)≤β(t);f(t,x)在区域G∶a≤t≤b,α(t)≤x≤β(t),上连续,且保证初值问题

的解存在。当t∈[a,b]时,有

则对任意满足α(a)≤A≤β(a)的常数A,问题(7)在区间[a,b]上总有一个解x(t),并满足不等式

函数α(t)和β(t)称为初值问题(7)的一对上下解。

定理1 假定且关于λ连续可微,则近似解(6)在[0,T]上一致有效,其与精确解的误差估计为

其中:xa(t,ε)由式(6)给出;T是任意有界的正常数;γ为与T有关的正常数;0<ε0≪1。
证明分别构造式(2)的上、下解[9-11]为:

其中γ为正常数,易知

对任意有界的T>0,当t∈[0,T]时,由Lagrange中值定理

由引理可知,xa(t,ε)在[0,T]上一致有效,且xa(t,ε)与x(t,ε)的误差估计为
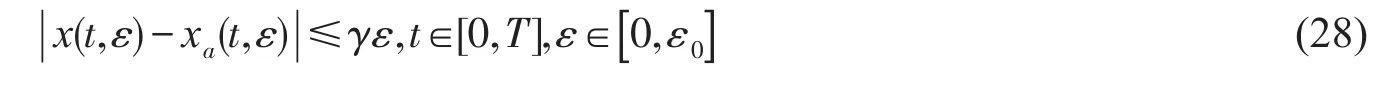
可知定理成立。
2 长时间渐近分析
为了获得在更长时间范围内的一致有效渐近解,可选用多重尺度法。如果选用导数多重尺度法,则会出现不可消去的长期项;如果使用两变量线性多重尺度法,则需取到ε2阶,增大了求解的难度。为避免出现以上两种方法的弊端,选用非线性两变量尺度法对式(2)求解。

将x(t0,t1,ε)关于ε幂级数展开

取x(t0,t1,ε)的前两项,并将其代入式(29),有

此时,式(31)关于ε的阶数展开,可得

通过变量分离可得式(32)的解


对式(33)求解x1(t0,t1),将式(35)代入式(33),此时,r(t1),h(t1),k(t1)以及均可视为常数,与式(2)式相比,式(33)为标准的一阶线性微分方程。取其特解

为消除长期项,使得关于x(t0,t1,ε)的渐近展开式一致有效需是有界的,即带有项的系数为零,取此时θ(t1),c(t1)为常数,取θ(t1)=1,则有

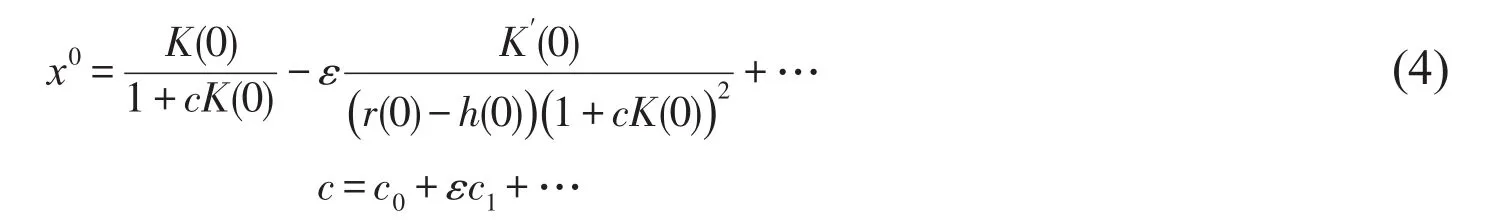
令
将式(40)代入式(39),有
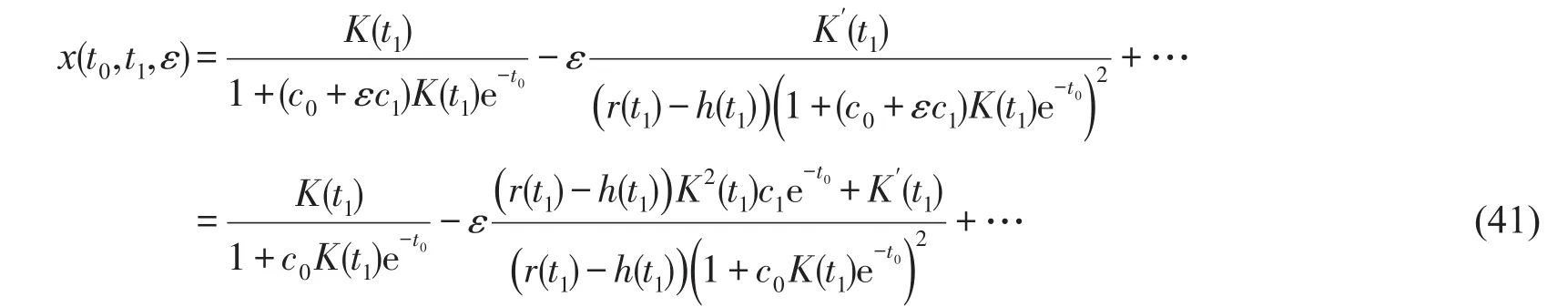
则

将式(42)代入式(41),得

其中t0由式(37)给出。
3 结 语
1)讨论的具有时变收获特性的Logistic模型更符合实际情况,有利于种群研究中对有经济价值的动植物种群对有害物种的控制。
2)采用匹配法构造其在[0,T]上的近似解,通过上下解法证明近似解的一致有效性,并给出近似解与精确解之间的误差估计;选用非线性两尺度法,获得了在更长时间范围内,即上的渐近解。
[1]SHEPHERD J,STOJKOV L.The logistic population model with slowly varying capacity[J].Anziam Journal Electronic Supplement,2007,47:492-506.
[2]SHEN J H,ZHOU Z Y.Fast-slow dynamics in logistic models with slowly varying parameters[J].Communications in Nonlinear Science&Numerical Simulation,2013,18(8):2213-2221.
[3]王寿松.单种群增长的广义Logistic模型[J].生态数学学报,1990,5(1):21-25.
[4]李海龙.一类具有周期系数的单种群模型及其最优收获策略[J].生物数学学报,1999,14(4):394-402.
[5]NAYFEHA.Introduction to Perturbed Techniques[M].New York:John Weiley&Sons,1981:365-375.
[6]陈松林.具常投放率的反应扩散系统的渐近性质[J].生物数学学报,1995,10(4):134-137.
[7]刘树德,鲁世平,姚静荪,等.奇异摄动边界层和内层理论[M].北京:高等教育出版社,2012:145-151.
[8]Johnson R S.Singular Perturbation Theory[M].New York:Springer-Verlag,2005:157-183.
[9]周倩,陈松林.一类非线性奇摄动问题边界层与边值的关系[J].合肥学院学报,2011,21(4):12-15.
[10]周倩,陈松林.一类非线性方程Robin问题的激波位置[J].安徽工业大学学报(自然科学版),2012,29(4):375-380.
[11]孙龙,陈松林.一类具有慢变特性的Logistic模型解的合成展开[J].安徽工业大学学报(自然科学版),2015,32(1):65-69.
责任编辑:丁吉海
AsymptoticAnalysis for a Class of Time Varying Harvested Logistic Model
ZHOU Qian1,JIANG Xiaohui2,CHEN Songlin2
(1.Hehai University Wentian College,Ma'anshan 243031,China;2.School of Mathematics&Physics Science and Engineering,Anhui University of Technology,Ma'anshan 243032,China)
A class of the time varying harvested Logistic model with small parameters was studied.The matching method was empoyed to construct the approximate solution of the model,and the uniform validity of the approximate solution was proved via methods of upper and lower solution.At the same time,the error estimate between the approximate solution and the exact solution was given.According to the nonlinear method of multiple scales, the formal asymptotic solution for longer periods of time was obtained.
harvested Logistic model;approximate solution;matching method;the method of multiple scales
O 175.1
A
10.3969/j.issn.1671-7872.2016.04.014
1671-7872(2016)04-0384-06
2016-01-14
安徽省高校自然科学研究重点项目(KJ2016A084);河海大学文天学院校级课题(WT15008)
周倩(1986-),女,安徽马鞍山人,讲师,研究方向为微分方程的渐近理论。
陈松林(1964-),男,安徽安庆人,教授,研究方向为微分方程的渐近理论。
