天然气水合物降压开采储层稳定性模型分析*

程家望，苏 正，吴能友

（1. 中国科学院广州能源研究所，广州 510640；2. 中国科学院天然气水合物重点实验室，广州 510640；3. 中国科学院大学，北京 100049）



天然气水合物降压开采储层稳定性模型分析*

程家望1,2,3，苏 正1,2†，吴能友1,2

（1. 中国科学院广州能源研究所，广州 510640；2. 中国科学院天然气水合物重点实验室，广州 510640；3. 中国科学院大学，北京 100049）

摘 要：储层稳定性是天然气水合物开采所面临的关键问题。本文基于多孔介质流体动力学和弹性力学，建立了天然气水合物降压开采储层稳定性数学模型，包括储层沉降和井壁稳定性分析两个方面，并以墨西哥湾某处水合物藏的基本参数为例，进行了水合物降压开采储层稳定性的模拟计算。结果表明，在水合物降压开采的过程中，孔隙流体压力降低导致了储层的沉降，最大的沉降发生在井壁附近，水合物分解会加剧储层的沉降；降低井孔压力会造成井壁破坏的潜在危险，在井壁附近，周向和垂向应力达到最大处容易发生失稳破坏，地层的水平应力差会增加井壁的不稳定性。

关键词：天然气水合物；降压开采；储层沉降；井壁稳定性

0 前 言

天然气水合物已成为当今地球科学和能源工业发展的一大热点。天然气水合物能否在未来能源结构中有所贡献，关键在于能否被经济有效地开采[1]。天然气水合物的开采方法有降压、注热、注化学剂法等，而降压法被视为目前最经济可行的方法[2]。降压法主要是通过开采井抽取水合物储层内的流体而达到减小储层内部压力的目的，当储层内压力低于水合物相平衡压力时，水合物就会发生分解。

然而，海洋天然气水合物沉积体通常胶结差、抗剪强度弱，水合物在沉积孔隙介质间起胶结作用[3-5]。降压开采时，压力降低会导致储层内的应力改变和垂向形变，大多数情况还会造成剪应力的增大，而剪应力增大可能造成剪切破坏[6]。水合物的分解则会导致储层岩土力学特性的改变，如有效渗透率、孔隙度和力学模量。因此，水合物降压开采可能造成储层的失稳破坏，影响开采的安全性和高效性，甚至会危及海底的工程设施。综上可知，储层稳定性是天然气水合物开采所面临的关键问题，而在以往天然气水合物开采潜力评价中往往忽略对水合物储层稳定性的评估[7]。

目前，已有学者对天然气水合物开采储层稳定性进行了初步研究。KIMOTO等[8]基于化学–热力学–力学的耦合分析，提出了预测甲烷水合物分解导致的地层沉降模型。该模型采用质量守恒、动量守恒和能量守恒描述水合物的分解，运用多孔介质和BIOT理论进行岩土力学分析，采用非饱和土的弹–粘塑性模型，同时考虑了基质吸力、水合物饱和度以及温度的影响。KIM等[9]提出了水合物分解过程中在流体流动和岩土力学过程之间的双向耦合模型。该模型不仅考虑流体孔隙压力对岩土力学过程的影响效应，同时分析岩土力学过程对流体孔隙体积变化的影响。由于上述两个模型只考虑地层的沉降变形，未对井壁稳定性进行研究，不适用于评估水合物开采过程中的储层稳定性。

FREIJ-AYOUB等[10]提出了含水合物沉积地层中钻孔的井壁稳定性模型。此模型将多孔介质中水合物的热力学稳定性与流体流动、热传导以及力学变形等过程相耦合，将地层的力学特性设为多孔弹塑性，把水合物分解释放的甲烷气体和孔隙水看作一个流体相，地层的破坏条件由Mohr-Coulomb屈服准则来判断，稳定性用应力场中孔隙压力的变化来分析。但该模型没有考虑水合物分解对流体渗透性的影响，而渗透性是水合物降压开采影响压降传递和产气率的重要参数。

基于前人的研究和认识，本文将储层沉降和井壁稳定性结合到降压开采过程中，建立了天然气水合物降压开采储层稳定性数学模型，同时考虑了孔隙度和渗透率等地质参数变化的影响，并将该模型运用于墨西哥湾某处水合物藏，进行水合物降压开采的模拟计算，分析了水合物降压开采所导致的储层沉降和井壁稳定性问题。

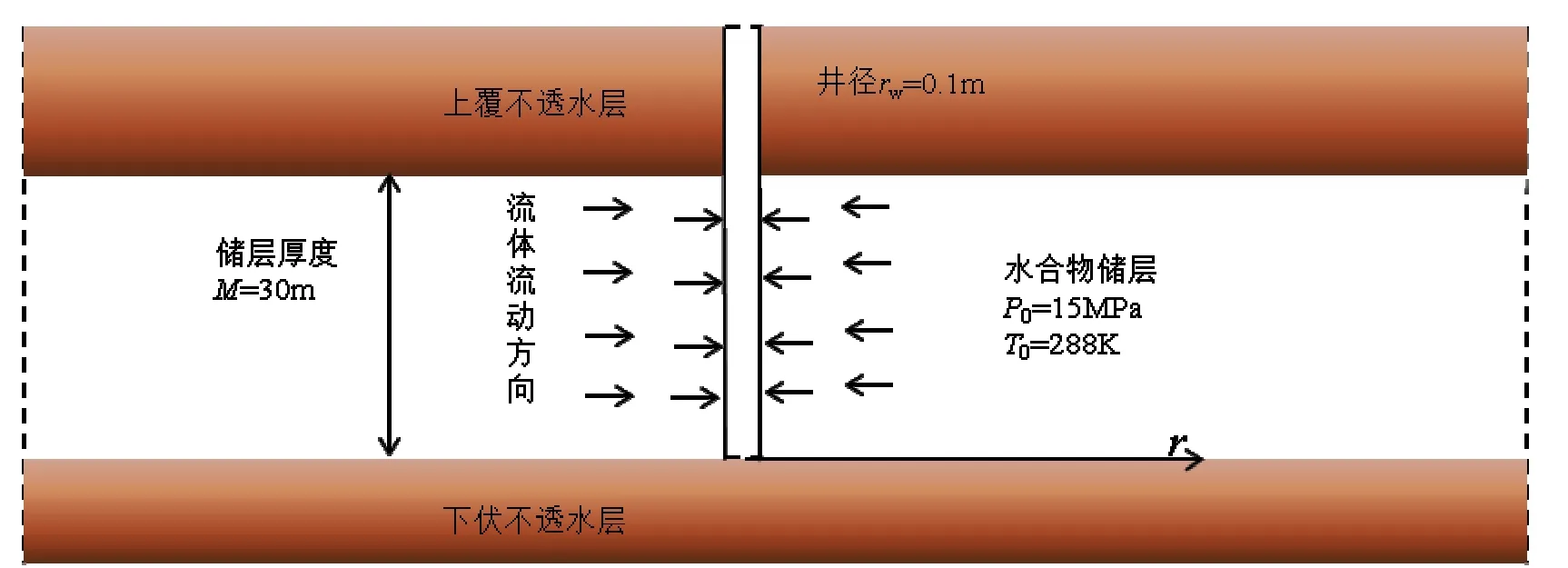
图1 天然气水合物降压开采概念图Fig. 1 Schematic diagram of hydrate reservoir for gas hydrate production by depressurization

1 数学模型

天然气水合物开采是一个复杂的过程，主要包括多相流体流动、热对流和热传导、热力学和化学反应以及地层的沉降变形[8,11]。而降压开采主要依赖于压降在水合物储层内的传递。压力降低会改变储层内的应力场，并导致储层垂向沉降变形。因此压力变化是分析水合物降压开采储层地质稳定性的关键。

为了研究水合物降压开采对储层稳定性的影响，构建相对简单易用的数学模型，对模型进行如下假设或简化：（1）假设水合物分解为等温过程，即水合物分解过程中储层温度不发生变化，而事实上水合物分解会导致储层温度降低，并使水合物分解所需的平衡压力降低，不利于水合物分解和开采，但本文并不直接描述水合物分解的热力学和动力学过程，只视压力变化为水合物分解和压力场函数的因子；此外，在含水合物的多孔介质中，降压导致的变形几乎是注热的十倍[8]。所以温度变化对储层稳定性的影响可以忽略；（2）水合物分解效应通过水合物饱和度来反映。水合物饱和度的减小会造成有效孔隙度的增加，而有效孔隙度的变化直接影响着渗透率、贮水率和内聚力等地质和力学参数的变化；（3）假设储层沉积体为均质各向同性，水平等厚，横向无限延伸，岩土力学特性为线性多孔弹性，这在海洋天然气水合物研究中是常见并合理的；（4）垂直井穿透整个储层，流体水平流动且服从Darcy定律，且上覆和下伏沉积体为不透水层。这种假定基于水合物储层往往为薄层沉积体，储层中的流体流向井孔可基本视为水平流动并服从Darcy定律；另一方面这种假设不考虑垂向上的流体流动，也忽略上下层中的流体流向井孔；（5）假设分解产生的气体被最大限度的抽取，忽略其对地层压力的影响。上述假设使整个模型呈明显简化的一维特征，增强了模型的可用性。

本模型运用多孔介质流体动力学分析降压过程中储层内的压力分布，只关注降压造成的压力变化以及相应的应力分布变化和垂直沉降，而不考虑水合物分解的具体过程。

1.1 储层内压力分布

压力降低会改变储层应力场，应力场的变化则会影响储层稳定性。因此，分析储层的稳定性首先要研究储层压力的变化。基于以上假设，根据承压含水层地下流体向完整井的非稳定运动模型[12-13]，建立柱坐标下储层内压力分布的控制方程：

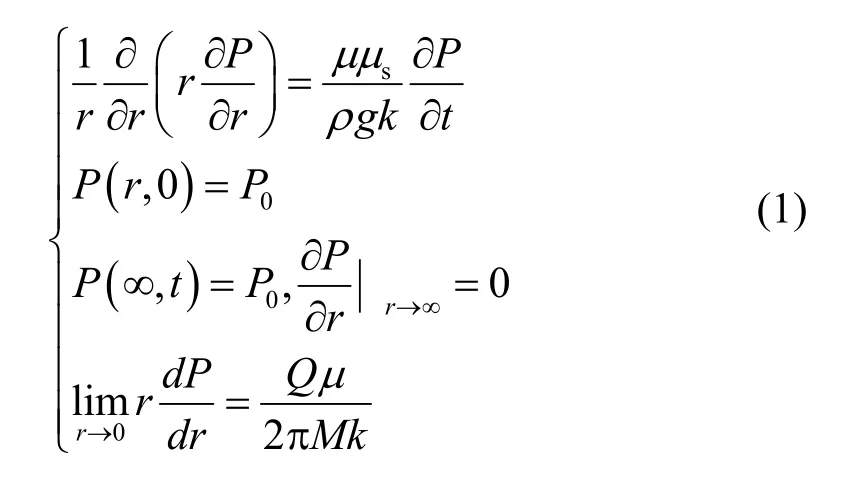
求解方程，则得到降压过程中储层压力水平径向分布函数：

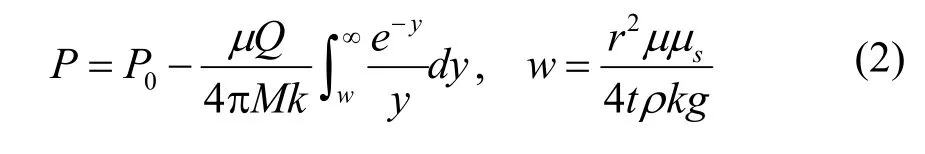
式中：P0为储层初始压力；P为降压后储层压力；Q为井孔水流量；M为储层厚度；μ为水粘滞性系数；k为渗透率；t为时间；ρ为水密度；μs为贮水率，；α为多孔介质压缩系数；β为水压缩系数。

设井孔半径为rw，井孔处压力为Pw，代入式（2）得：

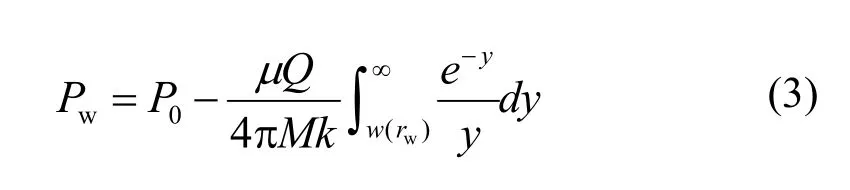
联立式（2）与式（3）可得：

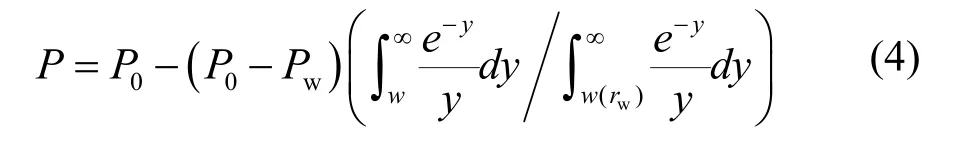
由式（2）和式（4）便可求解储层压力分布。压力是井孔压力或流体流量的函数，因此通过改变井孔压力或调节流量，即可实现降低储层压力的目的。

根据Kozeny-Carmen方程[14]，可知渗透率k：

水合物储层内有效孔隙度Ф为[2]：

式中：φ0为固有孔隙度。

由式（5）和式（6），则可得到：

式中：k0为储层中无水合物的绝对渗透率，SH为水合物饱和度。

根据（6）式，储层的贮水率可用下式表示：

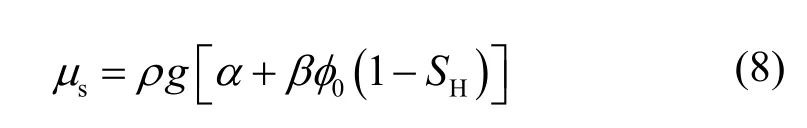
甲烷水合物相平衡的温度和压强的关系运用下式[15]：

式中：TD和PD是水合物分解的平衡温度和压力（Pa），T0为273.15 K，a = 0.034 2/K，b = 0.000 5/K2，c = 6.480 4。本模型采用降压开采的方法，假设水合物分解为等温变化，不影响储层内的温度。

1.2 储层沉降

降压造成的孔隙压力变化会改变储层内的有效应力，有效应力的降低会导致地层的沉降变形。这里假设地层的侧向受到限制，只有垂向上发生沉降变形。各向同性弹性多孔介质垂向上的固结沉降控制方程为[16]：

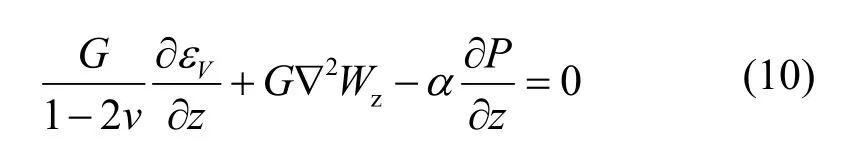
几何方程：

Terzaghi有效应力原理：

在Biot理论中，导致地层沉降的孔隙压力变化是在上覆荷载压力的作用下发生的，这与水合物开采过程中的储层孔隙压力变化不一致，这里将上面推导得到的压力分布式（4）引入到Biot理论中，并结合Terzaghi有效应力原理来计算沉降量[16-17]。

1.3 井壁稳定性

开采井改变储层原位应力的稳定状态，并导致井壁周围的应力集中。根据线性多孔弹性力学，垂直井周围的应力分布可描述为[18-19]：

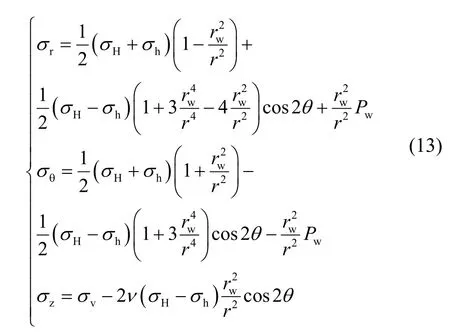
式中：σr为径向应力，σθ为周向应力，σz为垂向应力，Pw为井孔压力，v为泊松比，σH为最大水平地应力，σh为最小水平地应力，r为储层内到井孔的距离，θ为与最大水平地应力的夹角。这里同时要考虑有效应力原理，并以压应力为正。

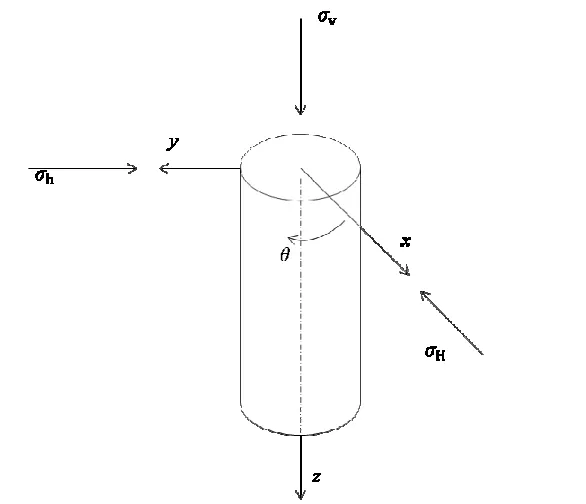
图2 垂直井井壁周围应力特征示意图Fig. 2 Schematic diagram of stress of a vertical borehole

井壁稳定性运用Mohr-Coulomb准则进行判断：

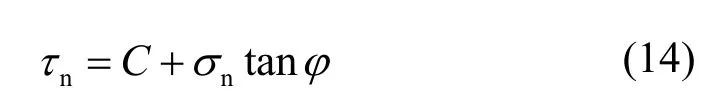
式中：τn为剪应力，σn为正应力，C和φ分别为内聚力和内摩擦角。

通过内聚力的线性软化来反映水合物分解对储层沉积物强度的影响[10]：

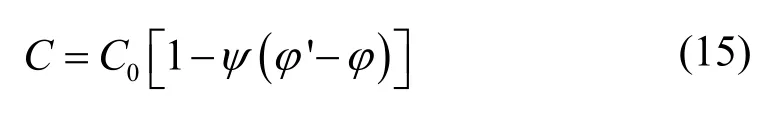
式中：C和C0分别是最终和初始内聚力，'φ和φ分别是最终和初始有效孔隙度，参数ψ设为1.2。

2 结果与讨论

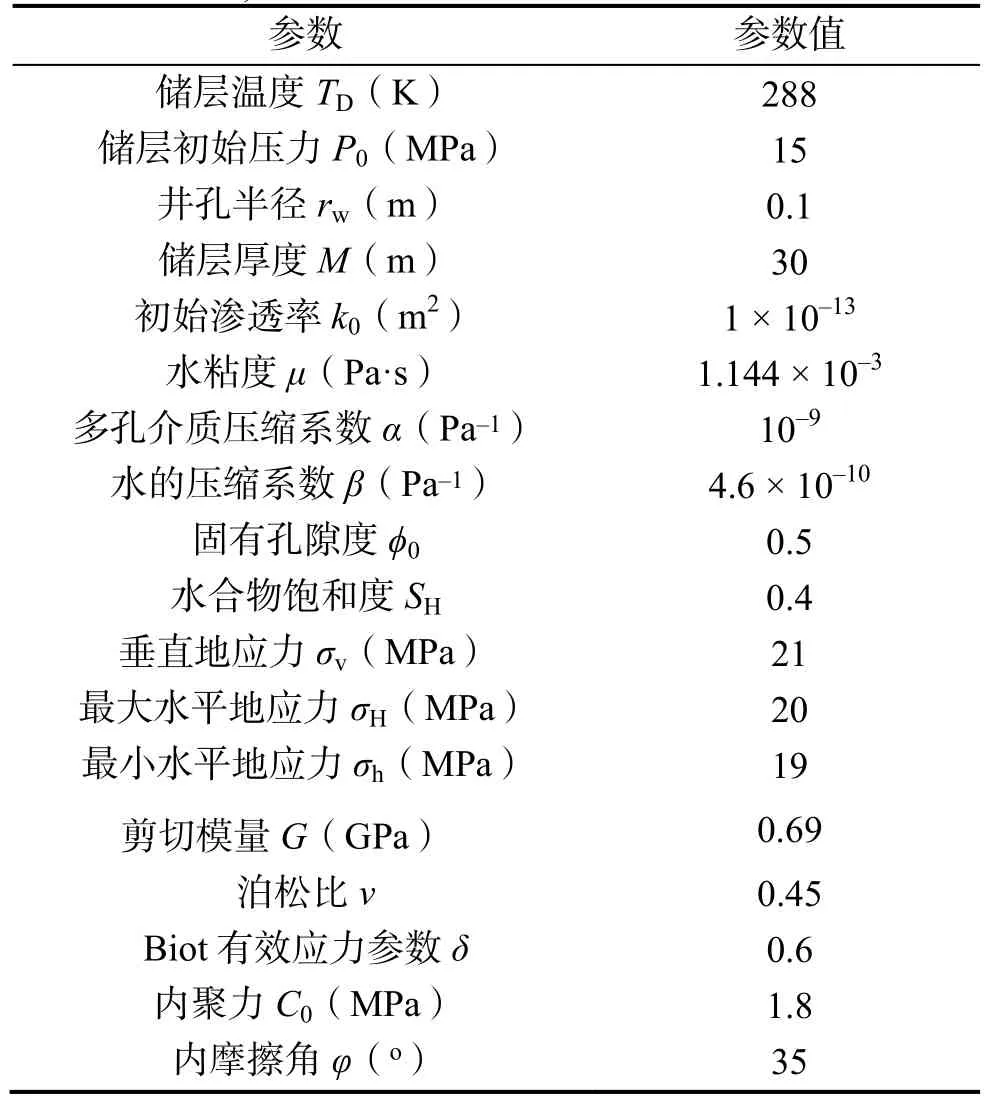
表 1 模型计算参数选取（参考墨西哥湾某处水合物藏）Table 1 Model parameters (based on a hydrate reservoir at the Gulf of Mexico)

该模型描述了垂直井降压开采过程中水合物储层稳定性问题，这里以墨西哥湾某处水合物藏的部分基本参数[10]为依据进行模拟计算，分析水合物降压开采所导致的储层沉降和井壁稳定性问题。表1列出了各参数的值，下面对模拟结果进行讨论。

2.1 压力分布特征

水合物降压开采是指降低含水合物沉积层内的压力，使其低于平衡压力，驱动水合物发生分解。因此，压力分布及其变化是储层稳定性问题研究的基础和关键着力点。降压可以通过两种途径实现：调节井孔流量和控制井孔压力。图3显示了分别在控制井孔流量和井孔压力条件下，储层内压力分布特征及其随时间的变化。井孔内压力最低，在井孔附近压力急剧变化；而在储层内距井孔较远处变化缓慢，最后接近储层初始压力。随着时间的变化，压降沿径向向储层内传播。由此可知，在井孔流量或井孔压力恒定时，增长开采时间可以有效地降低储层内压力。

根据式（9）计算得出储层内水合物保持相平衡稳定的最小压力为12.5 MPa，并在图中标出。因为水合物分解并不是瞬间发生，而且实际水合物分解时吸热会降低储层温度，这样就可能使相平衡压力相应减小，所以图中低于12.5 MPa的区域显示的是水合物可能发生分解的范围。

储层压力是井孔流量和井孔压力的函数，而且井孔流量越大或井孔压力越小，降压效果越好。图4显示了开采时间为1年，不同井孔流量和井孔压力情况下，储层压力分布特征。随着井孔流量的增大或井孔压力的降低，压降向储层内传播的更远更有效。分析储层压力分布的目的是为了分析储层的应力场，继而分析水合物降压开采对储层稳定性的影响。

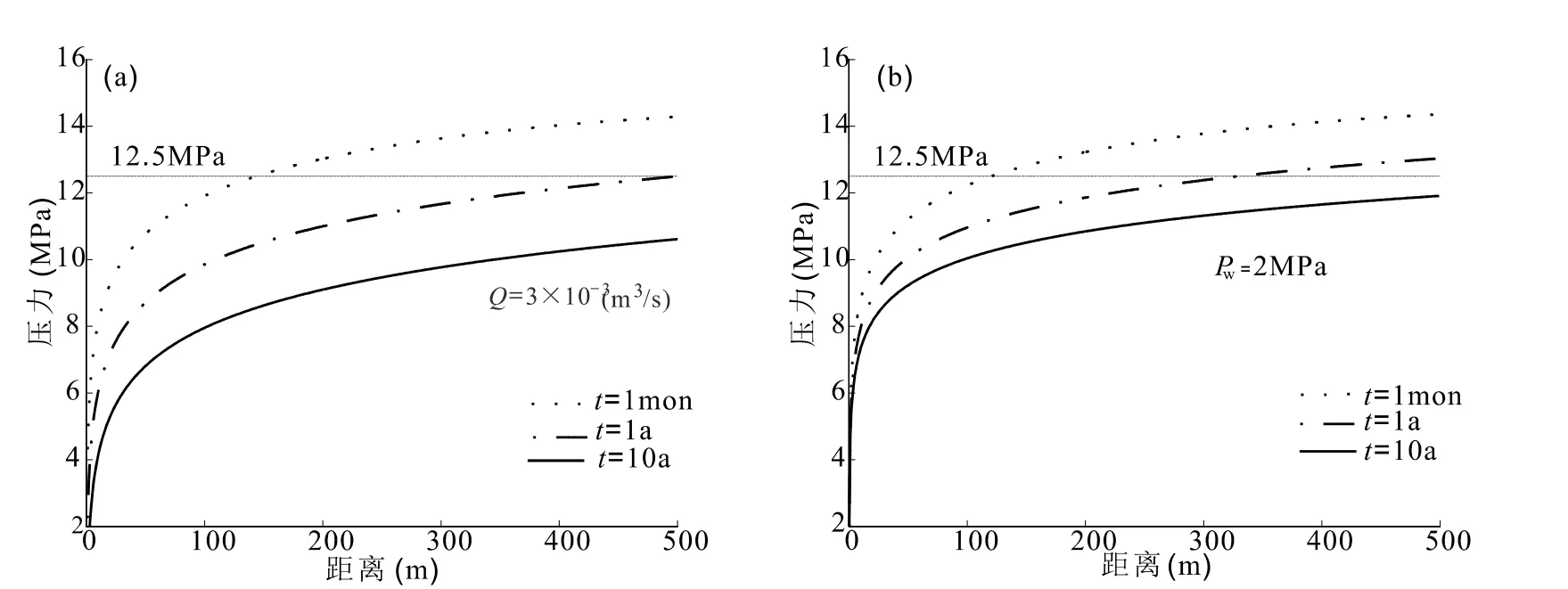
图3 水合物储层压力径向分布及变化，（a）为定井孔流量3 × 10−3m3/s，（b）为定井孔压力2 MPaFig. 3 Time variation of pressure in the vicinity of well in the reservoir for a given well flux 3 × 10−3m3/s (a) and a given well pressure 2 MPa (b), respectively

图4 储层压力径向分布特征，（a）为不同井孔流量，（b）为不同井孔压力Fig. 4 The pressure profiles in the vicinity of well in the reservoir for different well flux (a) and various well pressure(b), respectively

2.2 储层沉降分析

储层孔隙压力的降低导致沉降的发生，并且沉降的幅度取决于压力降低的大小。图5显示了分别在给定井孔压力（2 MPa）不同时间和给定时间（10年）不同井孔压力条件下，开采井附近储层的沉降情况。由图可以发现，最大的沉降发生在井壁附近，沉降量向储层内逐渐减小。随着时间的推进，沉降量增大。由图4b和图5b可知，降低井孔压力可以更有效地降低储层内压力，而结果则会导致更大的沉降。因此可知，沉降量与压力降低值成正相关。计算显示最大的沉降量低于0.08 m，即意味着垂直应变小于0.3%。如此小的应变不会造成储层失稳，因为储层的垂直压实超过5%才会有导致套管破裂的危险[6]。

水合物存在于沉积孔隙空间，是沉积体的组成部分，并起胶结作用，甚至支撑作用。因此，水合物降压分解必然与压降传递以及储层沉降相关联。图6显示开采时间为10年井孔压力为2 MPa，储层内存在水合物分解与无水合物分解两种情况下，沉降以及压降曲线的对比。存在水合物分解时沉降量增大，这意味着水合物分解越多，沉降越大。水合物分解效应会加剧储层的沉降。由图6a可以看到，两种情况下的沉降曲线在井附近几乎重合。图6b可以很好地解释这个现象，因为在井附近的压降曲线同样几乎重合。这说明井孔附近的岩土力学响应是由储层范围内的压降所驱动的[20]。

图5 水合物储层沉降特征，（a）为相同井孔压力不同时间，（b）为相同时间不同井孔压力Fig. 5 Settlement profiles for a given well pressure of time variation (a) and a certain time of various pressure (b), respectively

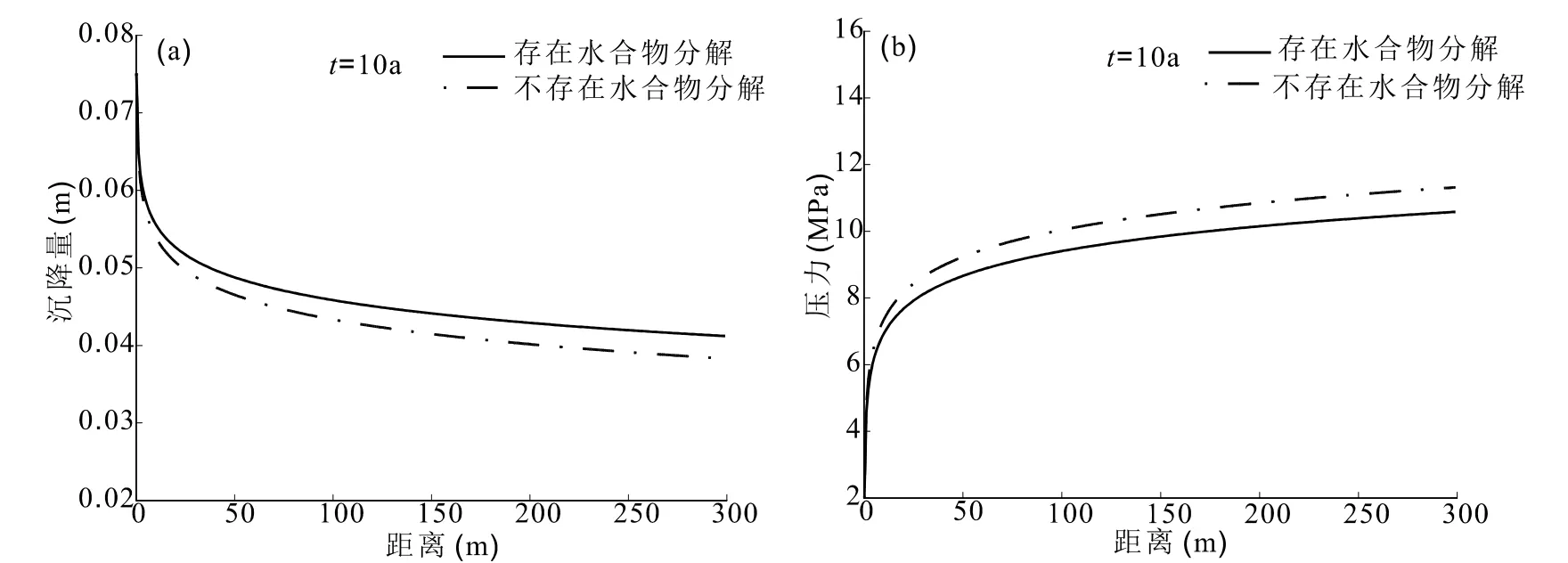
图6 存在水合物分解效应与无水合物分解效应两种情况的比较，（a）为沉降量的对比，（b）为压力降低值的对比Fig. 6 Settlement and pressure profiles for comparison of different conditions of hydrate decomposition (a) and no hydrate decomposition (b)

2.3 井壁应力分布和稳定性分析

井孔会改变储层原位应力的稳态，并导致井壁周围的应力集中。在降压过程中，井孔附近储层垂向、径向和周向应力分别表现出不同的变化特征。图7显示了在井孔压力4 MPa开采时间10年，井壁和井孔附近储层的有效应力分布。径向、周向和垂向应力都是角度的函数，但井壁上只有周向和垂向应力随角度变化，而径向应力不发生变化。径向和周向应力与井孔压力有关，所以改变井孔压力只影响径向和周向应力，而对垂向应力没有影响。井孔会导致井壁周围的应力集中，井壁破坏最可能发生在井壁应力最集中的地方。由于井壁上径向应力不发生变化，所以周向和垂向应力达到最大值处最可能首先发生剪切破坏。因此在井壁和

分析井壁稳定性需选择合适的判定准则[21-22]，这里选择在岩土力学中应用最广泛的Mohr-Coulomb准则进行井壁稳定性分析。Mohr-Coulomb准则认为岩土的破坏主要是剪切破坏，岩土强度是由岩土本身抗剪切摩擦的内聚力和剪切面上法向应力产生的摩擦力构成。根据Mohr-Coulomb准则，当Mohr圆达到破坏线时发生剪切破坏，用式（14）定义的破坏线来说明井壁破坏的临界条件。图8a显示了不同井孔压力下应力状态的Mohr圆，据此可知，降低井孔压力会不可避免的导致井壁破坏的危险。因此在这种情况下，钻井设计必须要保证井壁的稳定性。

然而，矛盾的是降低井孔压力有助于水合物的分解，要保证井壁的稳定又必须维持一定的井孔压力。所以本文可以帮助选择一个最合适的井孔压力：既可以保证井壁稳定，又可以更有效地降低储层孔隙压力。

在FREIJ-AYOUB等的模型中，墨西哥湾的水平应力被视为是各向相等的。然而在墨西哥湾的Atwater 峡谷和Walker海脊都有因存在水平应力差而导致钻井破坏的报道[23]。为了说明水平应力差的影响，图8b显示了不同水平应力情况下应力状态的Mohr圆。如图所示，当最大水平应力不变时，随着最小水平应力的减小，即水平应力差的增大，井壁会更不稳定，存在发生剪切破坏的危险。这意味着地层存在水平应力差会增加井壁的不稳定性。因此，在水合物藏开采前的地质背景调查和潜力评价中，地层内的水平应力差是需要考察的重要参数。

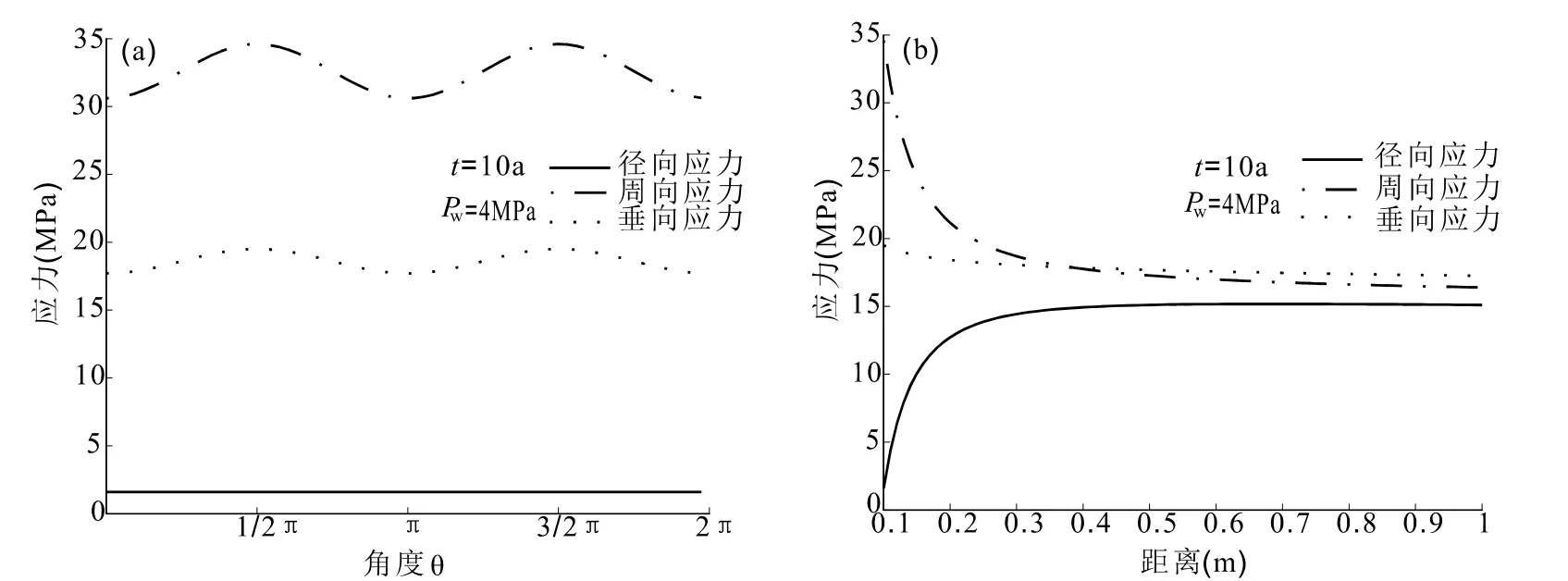
图7 有效应力分布特征，（a）为井壁应力分布，（b）为井孔附近储层应力分布Fig. 7 The effective stress distribution at the wellbore wall (a) and near the wellbore of directionθ=π/2 (b)

图8 τn-σn面上的Mohr-Coulomb 准则和在井壁不同应力状态下的Mohr圆，（a）表示不同井孔压力情况下应力状态的Mohr圆，（b）为不同水平应力差情况下应力状态的Mohr圆Fig. 8 Mohr-Coulomb criterion inτn-σnplane (a) and Mohr’s circle corresponding to the stress states under various conditions (b)

综合上述分析可知，在所研究的墨西哥湾某处水合物藏，降压导致的储层沉降不会造成开采过程中的安全性问题，但是存在井壁破坏的危险，因此降压开采过程中需要特别注意保证井壁稳定。

本模型基于多孔介质的流体动力学和弹性力学，分析了天然气水合物降压开采过程中储层孔隙压力的变化以及相应的应力变化和垂直沉降。模型假设水合物分解为等温过程，控制水合物分解的主要因素为孔隙压力的降低，水合物分解区随着压力降低向储层内延伸，模型计算得到的水合物分解区可能会大于水合物实际发生分解的区域。然而根据分析结果，储层稳定性问题主要集中在井壁附近，所以分解区边缘的误差不会影响模型的适用性。

3 结 论

本文建立了天然气水合物降压开采储层稳定性模型，运用多孔介质的流体动力学和多孔弹性力学，将储层沉降和井壁稳定性结合到水合物降压开采过程中，根据结果可以发现降压对水合物储层稳定性的显著影响。在水合物降压开采过程中，随着井孔流量的增大和井孔压力的降低，储层内压降传播得更远更有效。孔隙流体压力降低会导致储层的沉降，最大的沉降发生在井壁附近；水合物分解的越多，储层的沉降越大。降低井孔压力有助于水合物的分解，但同时可能导致井壁破坏的潜在危险；在井壁附近，周向和垂向应力达到最大处容易发生失稳破坏；地层中的水平应力差会增加井壁的不稳定性。

参考文献：

[1] MORIDIS G J, COLLETT T S, DALLIMORE S R, et al. Numerical studies of gas production from several CH4hydrate zones at the Mallik site, Mackenzie Delta, Canada[J]. Journal of petroleum science and engineering, 2004, 43(3/4): 219-238. DOI: 10.1016/j.petrol.2004.02.015.

[2] NAZRIDOUST K, AHMADI G. Computational modeling of methane hydrate dissociation in a sandstone core[J]. Chemical engineering science, 2007, 62(22): 6155-6177. DOI: 10.1016/j.ces.2007.06.038.

[3] MAKOGON Y F. Natural gas hydrates-a promising source of energy[J]. Journal of natural gas science and engineering, 2010, 2(1): 49-59. DOI: 10.1016/j.jngse. 2009.12.004.

[4] 沈海超, 程远方, 胡晓庆. 天然气水合物藏降压开采近井储层稳定性数值模拟[J]. 石油钻探技术, 2012, 40(2): 76-81. DOI: 10.3969/j.issn.1001-0890.2012.02.015.

[5] 宁伏龙, 蒋国盛, 张凌, 等. 影响含天然气水合物地层井壁稳定的关键因素分析[J]. 石油钻探技术, 2008, 36(3): 59-61. DOI: 10.3969/j.issn.1001-0890.2008.03.014.

[6] MORIDIS G J, COLLETT T S, POOLADI-DARVISH M, et al. Challenges, uncertainties, and issues facing gas production from gas-hydrate deposits[J]. SPE reservoir evaluation & engineering, 2011, 14(1): 76-112. DOI: 10.2118/131792-PA.

[7] 吴能友, 黄丽, 苏正, 等. 海洋天然气水合物开采潜力地质评价指标研究: 理论与方法[J]. 天然气工业, 2013, 33(7): 11-17. DOI: 10.3787/j.issn.1000-0976.2013. 07.002.

[8] KIMOTO S, OKA F, FUSHITA T, et al. A chemo-thermo-mechanically coupled numerical simulation of the subsurface ground deformations due to methane hydrate dissociation[J]. Computers and geotechnics, 2007, 34(4): 216-228. DOI: 10.1016/ j.compgeo.2007.02.006.

[9] KIM J, MORIDIS G J, RUTQVIST J. Coupled flow and geomechanical analysis for gas production in the Prudhoe Bay Unit L-106 well Unit C gas hydrate deposit in Alaska[J]. Journal of petroleum science and engineering, 2012, 92-93: 143-157. DOI: 10.1016/ j.petrol.2012.04.012.

[10] FREIJ-AYOUB R, TAN C, CLENNELL B, et al. A wellbore stability model for hydrate bearing sediments[J]. Journal of petroleum science and engineering, 2007, 57(1/2): 209-220. DOI: 10.1016/j.petrol.2005.10.011.

[11] HONG H F. Modeling of gas production from hydrates in porous media[D]. Calgary: University of Calgary, 2003.

[12] Bear J. Dynamics of fluids in porous media[M]. New York: American Elsevier Pub. Co., 1972.

[13] ZIMMERMAN R W. Flow in porous media[M]. London: Department of Earth Science and Engineeringe, 2002.

[14] FREEZE R A, CHERRY J A. Groundwater[M]. New Jersey: Prentice-Hall, 1979.

[15] JI C, AHMADI G, SMITH D H. Natural gas production from hydrate decomposition by depressurization[J]. Chemical engineering science, 2001, 56(20): 5801-5814. DOI: 10.1016/S0009-2509(01)00265-2.

[16] BIOT M A. General theory of three-dimensional consolidation[J]. Journal of applied physics, 1941, 12(2): 155-164. DOI: 10.1063/1.1712886.

[17] 李培超, 李贤桂, 卢德唐. 饱和土体一维固结理论的修正——饱和多孔介质流固耦合渗流模型之应用[J].中国科学技术大学学报, 2010, 40(12): 1273-1278. DOI: 10.3969/j.issn.0253-2778.2010.12.011.

[18] AADNOY B S. Stability of highly inclined boreholes (includes associated papers 18596 and 18736)[J]. SPE drilling engineering, 1987, 2(4): 364-374. DOI: 10.2118/16052-PA.

[19] FJAR E, HOLT R M, Horsrud P, et al. Petroleum related rock mechanics, volume 53[M]. 2nd ed. Amsterdam: Elsevier, 2008.

[20] RUTQVIST J, MORIDIS G J, GROVER T, et al. Coupled multiphase fluid flow and wellbore stability analysis associated with gas production from oceanic hydrate-bearing sediments[J]. Journal of petroleum science and engineering, 2012, 92-93: 65-81. DOI: 10.1016/j.petrol.2012.06.004.

[21] AL-AJMI A M, ZIMMERMAN R W. Stability analysis of vertical boreholes using the Mogi-Coulomb failure criterion[J]. International journal of rock mechanics and mining sciences, 2006, 43(8): 1200-1211. DOI: 10.1016/j.ijrmms.2006.04.001.

[22] ZHANG L Y, CAO P, RADHA K C. Evaluation of rock strength criteria for wellbore stability analysis[J].International journal of rock mechanics and mining sciences, 2010, 47(8): 1304-1316. DOI: 10.1016/ j.ijrmms.2010.09.001.

[23] BIRCHWOOD R, NOETH S. Horizontal stress contrast in the shallow marine sediments of the Gulf of Mexico sites Walker Ridge 313 and Atwater Valley 13 and 14-Geological observations, effects on wellbore stability, and implications for drilling[J]. Marine and petroleum geology, 2012, 34(1): 186-208. DOI: 10.1016/j.marpetgeo. 2012.01.008.

程家望（1990-），男，硕士研究生，主要从事天然气水合物开采储层稳定性的研究。

苏 正（1980-），男，博士，研究员，主要从事天然气水合物成藏机制和开采潜力评价、海洋地质和地质流体动力学、深层地热资源和增强型地热系统（EGS）研究。

A Geomechanical Stability Model Analysis of Hydrate Reservoir for Gas Hydrate Production by Depressurization

CHENG Jia-wang1,2,3, SU Zheng1,2, WU Neng-you1,2
(1. Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China; 2. Key Laboratory of Gas Hydrate, Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China; 3. University of Chinese Academy of Sciences, Beijing 10049, China)

Abstract:A model based on the dynamics of fluids in porous media and poroelasticity is developed for analyzing geomechanical stability of hydrate reservoir, which is a challenge for commercial gas production from hydrate reservoir. This model, including subsidence of hydrate reservoir and wellbore stability, is applied to Gulf of Mexico, where the basic parameters and the in situ stresses are publicly published. It is concluded that subsidence of hydrate reservoir occurs due to the changes in pore pressure and the maximum subsidence occurs near the wellbore; the more hydrates decompose, the larger subsidence occurs. Decreasing well pressure will induce potential wellbore failure and the borehole failure is expected to initiate at those positions where the tangential and vertical stresses reach the maximum value. The horizontal stress contrast increases the instability of wellbore.

Key words:natural gas hydrate; depressurization; subsidence; wellbore stability

作者简介：

通信作者：†苏 正，E-mail：suzheng@ms.giec.ac.cn

基金项目：国家专项课题（GHZ2012006003）；国家自然科学基金面上项目（41276057）；中国科学院广州能源研究所所长培育专项（Y407P51001）

* 收稿日期：2015-09-16

修订日期：2015-12-24

文章编号：2095-560X（2016）01-0033-09

中图分类号：TK01；TE1；P736

文献标志码：A

doi：10.3969/j.issn.2095-560X.2016.01.006