中心管底部形状对浮标波能转换性能影响的实验研究*
2016-03-28陈天祥伍儒康吴必军
李 猛,陈天祥,伍儒康,吴必军
(1. 中国科学院广州能源研究所,广州 510640;2. 中国科学院大学,北京 100049)
中心管底部形状对浮标波能转换性能影响的实验研究*
李 猛1,2,陈天祥1,2,伍儒康1,2,吴必军1†
(1. 中国科学院广州能源研究所,广州 510640;2. 中国科学院大学,北京 100049)
摘 要:为改善中心管振荡水柱式波力发电浮标的能量转换性能,对中心管底部设计了4种模型并在造波水槽中进行实验研究。试验结果表明,直管型中心管俘获宽度比最小,实验测得最高为4.12%,底部有一定锥度的模型会提高俘获宽度比,目前实验最高为19.25%,并出现较高的双峰值,提高了通频带,峰值周期也随锥度的不同出现了移动。试验得到的较佳模型需要进一步优化和实验,为设计适应不同海况的发电浮标提供基础数据。
关键词:波力发电浮标;模型;中心管;俘获宽度比;波周期
0 引 言
振荡水柱波浪能发电装置具有结构简单、制造成本低、没有水下运动部件、可维护性强、海生物附着影响小、性能可靠等优点。中心管振荡水柱波能发电装置由一个中间掏空带有一根长形管道的圆柱型浮体和空气透平机组构成,圆柱型浮体的尺寸远小于波长,浮体俘获波浪能的能力同波浪入射的方向无关。在波浪作用下,圆柱型浮体主要做垂荡运动,从而导致中心管内的水柱在水管内做相对振荡运动,振荡运动的水柱面相当于一个活塞,推动气室内的空气往复运动,从而使气室内的空气获得动能,运动的空气通过一个喷气口推动空气透平旋转,从而带动发电机发电[1]。该类型波能发电装置的工作原理如图1所示。
自1947年日本益田善雄成功研制波力发电灯浮标以来,该技术已得到一定范围的应用[2-3]。为探索2.4 m直径浮标水下浮体形状对波能吸收性能的影响,吴藻华等[3]于1984年通过试验研究得到水下浮体形状取球形或部分球形的浮标波能转换性能较好,但其能量俘获宽度比最高约为16%,而且通频带较窄,同年英国的贝尔法斯特女王大学WHITTAKER等[4]对一个直径3 m、中心管直径0. 7 m的发电浮标1/10模型进行了试验,试验研究表明不同的阻尼俘获宽度比不一样,最高达到了50%,通频带很窄,阻尼变小后通频带变宽,最高俘获宽度比减少,甚至出现了双峰值,但此双峰值俘获宽度比最高为10%左右。1994年,黄国樑等[5]针对前期研究的发电浮标在波浪周期短、波高小发电量不能满足需求的条件下对2.4 m浮标的发电性能进行了进一步试验研究,研究表明通过减少发电浮标质量移动了响应周期,但俘获宽度比未见提高,最高大概为14.6%,通过适当加长和加粗中心管可提高俘获宽度比,最高达到了25%。中国科学院广州能源研究所通过对对称翼型透平的研究,于1983年12月成功研制出新型的航标灯用中心管波力发电装置BD101型波力发电装置[6],随后又有改进后的BD102A型、BD102B型、BD102C型等装置投入小批量生产并使用[7],但并未对发电浮标的形状进行优化。近年来,葡萄牙的FALCÃO等[8-9]研究了中心管分成两个不同直径的圆筒并用锥形过渡段连接起来的浮标的动力响应,进行模拟计算,并未见相关试验研究成果报道。
从文献资料可知,目前国内外学者主要对2.4 m 及3 m、一般工作在2.5 ~ 3.5 s周期范围内发电浮标进行了能量转换性能试验,但对其他尺度可能有更广泛用途的海洋仪器供电浮标波浪能量转换特性研究较少,对于中心管底部形状变化对能量转换性能影响的实验研究也未见相关文献报道。为此本文设计了四种不同中心管底部形状的点吸收振荡水柱式波能转换浮标模型,测算其在不同波浪周期下的俘获宽度比,并通过比较选出较佳模型。
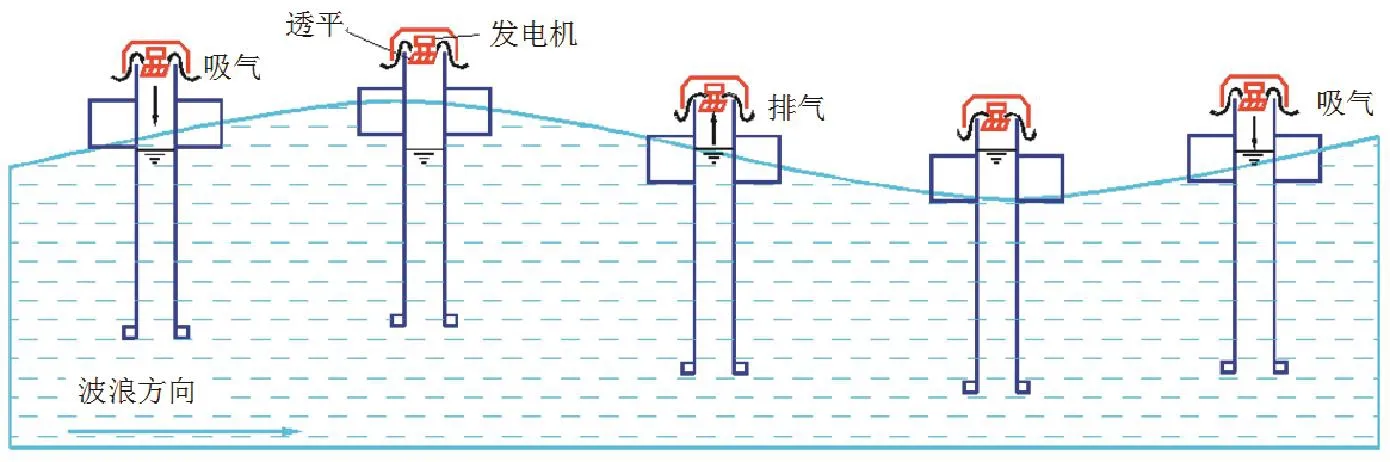
图1 波力发电浮标工作原理图Fig. 1 The operating principle of wave power generating buoy
1 实验部分
1.1 试验装置和方法
试验在中国科学院广州能源研究所海洋能实验室的造波水槽中进行。水槽宽1.2 m,高1.2 m,长50 m。一端装有计算机控制的变频电源伺服电机驱动的推板式造波机,推板宽1.16 m、高1.2 m,推板最大行程40 mm,可造规则波和不规则波。另一端为端部消波装置,水槽中间部分为试验段,通过此处的玻璃墙可以清楚地观察装置的运动情况。图2为试验装置布置简图。
在距离造波机大约8 m处装有一电容式波高仪,可以测量入射波波高;在距离造波机约17 m处放置试验模型,在模型气室顶部安装有另一电容式波高仪YWS100-AXX,用于测量气室内水位的相对波动;气室顶部还装有测压口,用PY301差压变送器测量气室内相对压力。入射波的波高数据由SDA1000传感器数据采集系统采集,由计算机控制,采样频率为20 Hz;气室内的水位变化和气压相对变化被相应的传感器获取,通过采集卡进行同步采样,由计算机控制,采样频率为16 Hz。
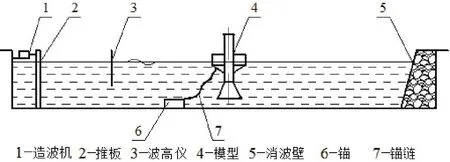
图2 试验装置布置简图Fig. 2 The layout diagram of experiment device
相关物理量计算公式[10]如下。
气室平均输出气流功率NA:
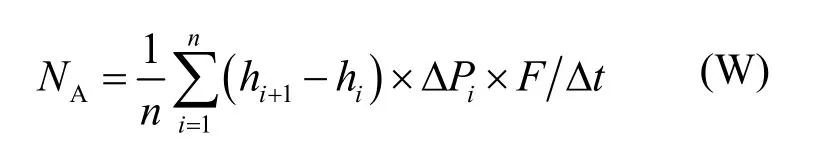
式中:ΔPi为第i点气室内相对压力(Pa);hi和hi+1为第i和i+1点气室内水位(m);F为气室截面积(m2);n为采样总点数;Δt为采样时间间隔(s)。
入射波功率NW:
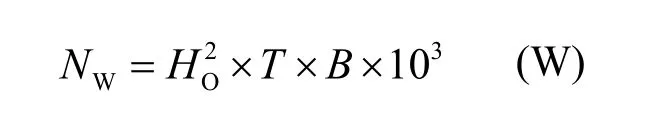
式中:HO为入射波浪高(m);T为入射波周期(s);B为浮体迎波宽度(m)。
气室俘获宽度比η:
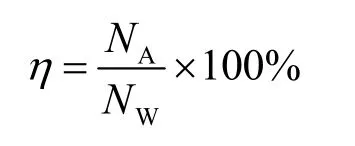
气室平均气流量Qav:
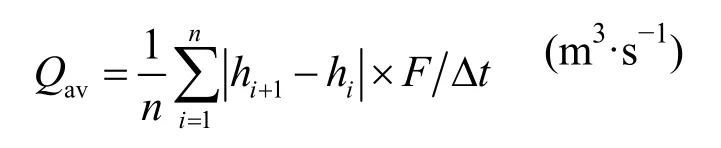
气室平均气压△Pav:
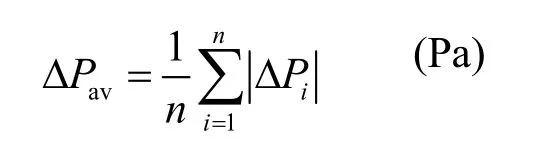
1.2 试验模型方案
制作了4种模型进行试验,为了节省成本,试验模型做成可拆卸的,4种模型简图及主要参数见图3,图4为制作的试验模型和试验实物图。
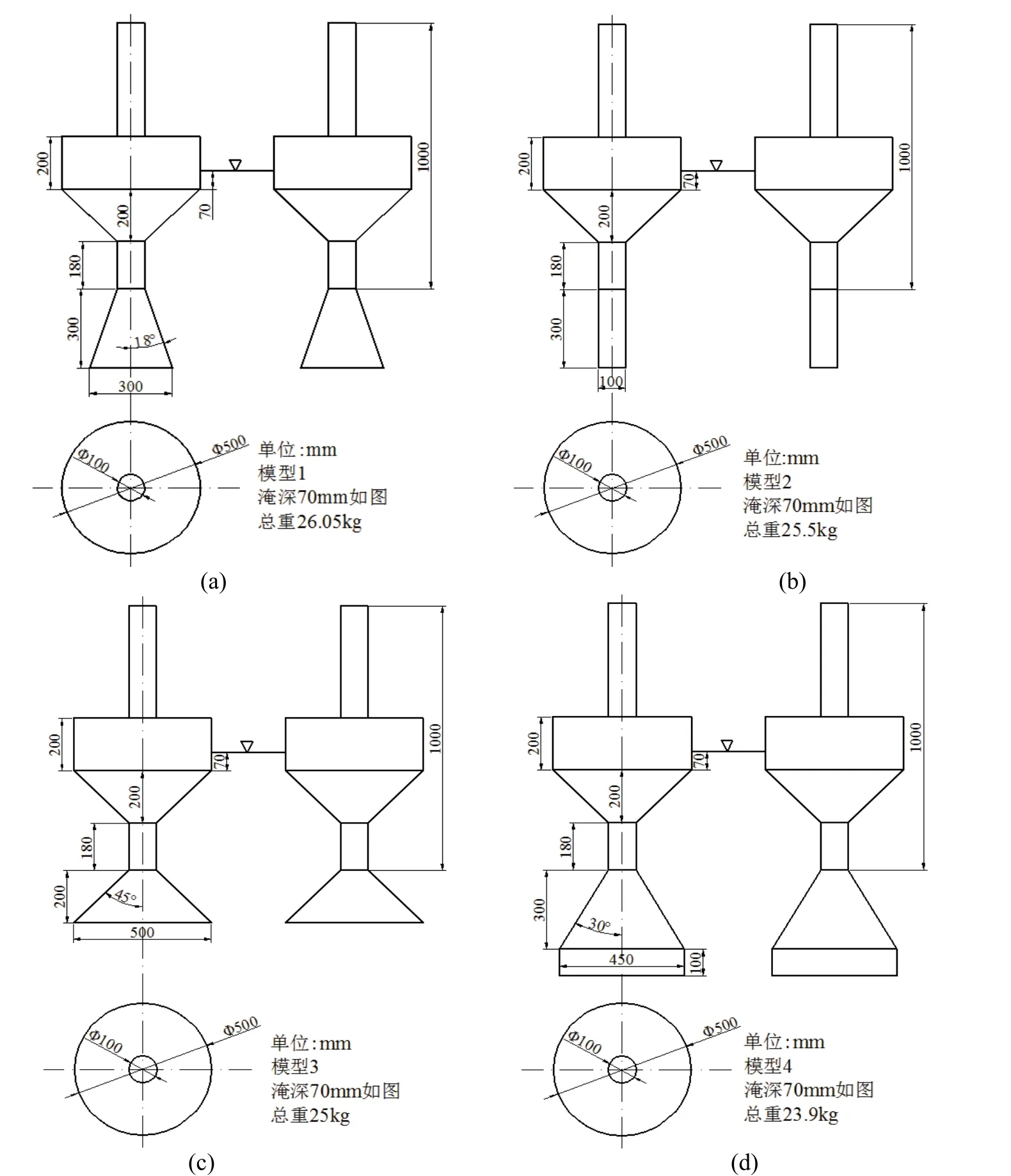
图3 4种模型简图及主要参数Fig. 3 Four model diagrams and main parameters
试验水槽水深0.9 m,锚链长度为1.71 m,锚泊挂点为一固定点,在模型的筒内放入适当的配重砝码使其淹深大概达到一固定值70 mm,装置气室顶部设有D = 20 mm的圆形气孔。在上述条件不变的情况下,使用造波机造推程为30 mm的不同周期波浪,波高约0.1 m,研究这4种模型的气室俘获宽度比随波周期的变化关系。为保证试验所测得数据的准确性,提高试验可信度,在每个试验条件下都重复试验3次。根据上面相应公式,对试验所得数据进行计算处理,由计算结果比较得出较佳试验模型。

图4 试验模型Fig. 4 Experimental models
2 结果与讨论
实验测量了入射波的波高和周期,以及中心管内的液位高度和气室内气压差的变化情况。据试验所测得的数据计算每一个周期点下的气室俘获宽度比,可得模型在不同波浪周期下的气室俘获宽度比,将结果示于图5和表1。
从试验得到的数据可以看出,管内的水柱相对于中心管做近似周期运动,气压差也呈正弦变化规律,例如模型1在波周期为1.1 s时的数据如图6。
从试验结果可以看出,模型2性能最差,最佳响应点时的俘获宽度比仅为4.12%;模型3和模型4次之,最佳响应点时的俘获宽度比分别为6.51%和9.95%;模型1性能最好,最佳响应点的俘获宽度比为19.25%。从俘获宽度比和波周期的关系图可以看出,模型1的曲线具有双峰特性,最佳响应周期附近均有较好的俘获宽度比,说明其响应波周期较宽,这对于实海上多种周期叠加的波浪吸收转换具有很好的实用价值。
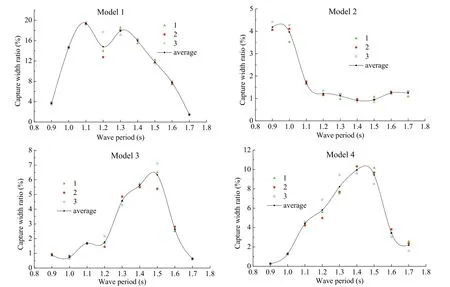
图5 俘获宽度比随波周期的变化曲线Fig. 5 The capture width ratio along with the change of wave period
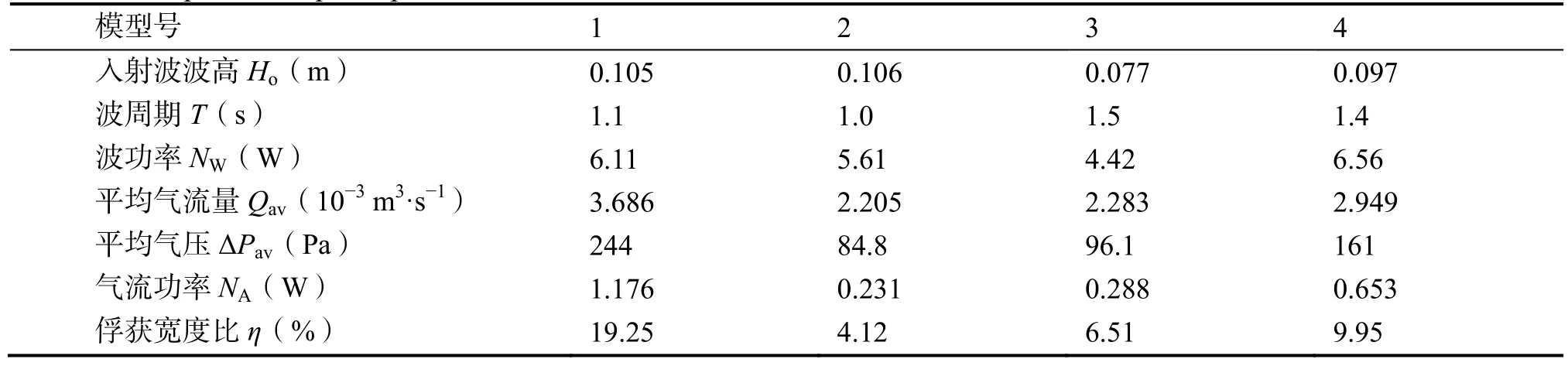
表1 各模型最佳响应点的性能Table 1 The optimum response performance of each model
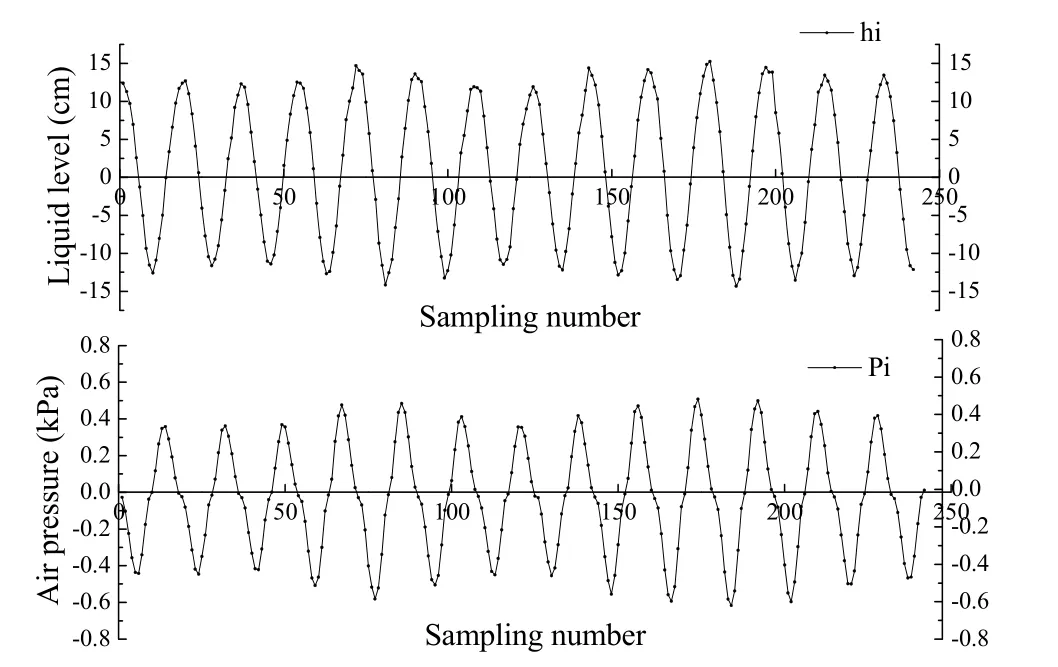
图6 来自中心管内的采样数据Fig. 6 Sampling data from the center pipe
模型2的底部为与中心管连接的等直径直筒,而其他三种模型的底部均采用了锥形变径段,对装置的俘获宽度比均有一定的提高。由俘获宽度比曲线图可以看出,较佳响应周期受到锥形变径段的影响很大,通过调节锥形变径段的角度可以改变装置的垂荡固有周期,使之接近要求的波浪周期,以得到较高的俘获宽度比。试验时,装置随波做近似的简谐运动,中心管内的水面接近平静水位,以模型为参考系,底部的水在通过变径段后,根据流体力学中的连续方程可知水流速度变大,因此气室内的气体改变变大,气流量和气压差也变大,这样就可可以获得更高的功率,装置的俘获宽度比也相应提高了。比较模型1和模型3,模型3的锥形变径段开口过大,装置在垂直方向运动时会受到很大的阻力,模型运动幅度变小,从而影响其俘获宽度比。对比模型1和模型4,锥形变径段没有较大区别,但是模型4的最下部有一段圆筒,增加的圆筒段并没有使俘获宽度比得到提高。在试验时,模型4出现了较为明显的纵荡和横荡运动,显然装置的垂荡运动会被削弱,故俘获宽度比也会降低。从几何尺寸可以看出,模型1相对于模型3、模型4表面积小,所用钢材少,造价较低,宜采用。
3 结论与展望
直管型的中心管俘获宽度比特性较差,通过改变中心管底部形状可以移动装置的垂荡固有周期,使之接近要求的波浪周期,以便得到较高的俘获宽度比。有合适角度的锥形变径段作为中心管底部的装置不仅有较高的俘获宽度比,目前模型试验达到19.25%,而且出现较高的双峰特性,拓宽了通频带。较高通频带和峰值周期的移动在实际应用中有重要意义。在接下来的试验研究中,可以改变配重以达到淹深的变化,来研究其俘获宽度比;改变气室顶部的开口大小,研究其对俘获宽度比的影响;改变锚泊系统的锚链长度以及锚链和模型的连接位置,研究其俘获宽度比的变化;在浮体尺寸不变的情况下,还可以考虑适当地改变中心管直径的大小,研究其对俘获宽度比的影响。
参考文献:
[1] 高祥帆, 蒋念东, 梁贤光. 静水池主动式气动型波能转换模拟实验装置[J]. 海洋工程, 1983, 1(1): 84-91.
[2] HEATH T V. A review of oscillating water columns[J]. Philosophical transactions: mathematical, physical and engineering sciences, 2012, 370(1959): 235-245. DOI: 10.1098/rsta.2011.0164.
[3] 吴藻华, 夏洪峰, 戴李民. 浮体形状对波能转换浮标性能的影响[J]. 海洋工程, 1984, 2(4): 59-62.
[4] WHITTAKER T J, MCILHAGGER D S, BARR A G. Wells turbines for navigation buoys[M]//TWIDELL J, RIDDOCH F, GRAINGER B, eds. Energy for rural and island communities. Oxford: Pergamon, 1984: 289-297.
[5] 黄国樑, 冯伯俊, 刘天威, 等. 改进波浪发电浮标性能的试验研究[J]. 海洋工程, 1994, 12(1): 104-110.
[6] 梁贤光, 高祥帆, 蒋念东, 等. 航标灯用波力发电装置[J]. 电工技术杂志, 1988(7): 9-12.
[7] 梁贤光, 杨光宇, 吴海明, 等. BD102G型航标用波力发电装置研制[J]. 可再生能源, 2014, 32(12): 1933-1938.
[8] FALCÃO A F O, HENRIQUES J C C, CÂNDIDO J J. Dynamics and optimization of the OWC spar buoy wave energy converter[J]. Renewable energy, 2012, 48: 369-381. DOI: 10.1016/j.renene.2012.05.009.
[9] FALCÃO A F O, HENRIQUES J C C, GATO L M C, et al. Air turbine choice and optimization for floating oscillatingwater-column wave energy converter[J]. Ocean engineering, 2014, 75: 148-156. DOI: 10.1016/j.oceaneng.2013.10.019.
[10] 梁贤光, 王伟, 杜彬, 等. 后弯管波力发电浮标模型性能试验研究[J]. 海洋工程, 1997, 15(3): 77-86.
李 猛(1988-),男,硕士研究生,主要从事波浪能转换技术研究。
吴必军(1965-),男,博士,研究员,主要从事海洋能转换技术研究。
Experimental Research on Effect of Center-pipe Bottom Shape on Performance of Wave Energy Conversion Buoy
LI Meng1,2, CHEN Tian-xiang1,2, WU Ru-kang1,2, WU Bi-jun1
(1. Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)
Abstract:For improving the energy conversion performance of the center-pipe oscillating water column(OWC)wave power generating buoy, four models with different center-pipe bottom shapes were designed for experimental research in the wave tank. The test results showed that the maximum capture width ratio is 4.12% and presents low energy conversion performance for the straight pipe buoy. For the cone pipe buoy, the capture width ratio can be improved (test ratio: 19.25%) with the cone pipe buoy, which presents higher double peaks. Different cone can result in different peak period. Considering the adaption of different sea conditions, further optimization and experimental validation are necessary for the tested models.
Key words:wave power generating buoy; model; center-pipe; capture width ratio; wave period
作者简介:
通信作者:†吴必军,E-mail:wubj@ms.giec.ac.cn
基金项目:国家自然科学基金(51276185,51579231)
* 收稿日期:2015-12-01
修订日期:2015-12-28
文章编号:2095-560X(2016)01-0015-05
中图分类号:TK212.+3;TV139.2+5
文献标志码:A
doi:10.3969/j.issn.2095-560X.2016.01.003
