基于单体扩张的端元提取算法

董安国，韩 雪，龚文娟



基于单体扩张的端元提取算法

董安国，韩 雪，龚文娟

（长安大学 理学院，陕西 西安 710064）

端元提取是高光谱混合像元分解的重要环节。为了提取高光谱图像的端元，本文基于线性表示理论与凸锥模型理论，论证了：与单体共面的单体外向量被单体的顶点向量线性表示时，表示系数必有负值，从而给出了理想情形下判别端元的充要条件，并在此基础上，针对非理想情形提出了一种提取端元的迭代算法。实验结果表明，算法提取端元的精度优于VCA算法、效率高于搜索算法，算法稳定性好，对噪声的敏感性低。

高光谱；凸锥模型；端元提取；单体

0 引言

高光谱遥感图像因具有较高光谱分辨率而成为当今遥感领域研究的热点，但其较低的空间分辨率和复杂的地物分布，导致影像中普遍存在混合像元，所以，基于高光谱图像进行精确的地物识别和分类，首先要对混合像元进行分解，而端元提取是混合像元分解的关键环节[1]。目前，端元提取算法较多，总体可以分为3类：穷举算法，投影算法与迭代算法。穷举是一种重复型算法，它的基本思想是，对问题的所有可能状态一一进行测试，直到找到解或全部可能的状态都测试过为止，穷举算法提取端元的精度高，但是算法运算量大，包括N-finder[2-3]算法，单体增长（simplex growing algorithm，SGA）[4-5]算法，其中N-FINDR算法，尽管无参数选择效果好，但因其搜索凸面体最大体积需遍历所有可能像元，计算量巨大。投影算法在进行端元提取时，计算速度相对较快，但是算法受噪声影响较大，精度不高。例如：像元纯净指数（pixel purity index，PPI）[6-7]算法，顶点成分分析（vertex component analysis，VCA）[8-9]算法，它们都是基于投影的算法，只是投影的方式不同。迭代是不断利用新值取代旧值，或者由旧值递推出变量新值的过程，此法运算速度快，工作量少，精度取决于算法的本身。例如，序列最大角凸锥（sequential maximum angle convex cone，SMACC）[10-11]算法，它虽然计算速度快，但不能保证获取端元的精度。

为此，论文在兼顾效率和精度的同时，基于线性表示理论，提出了一种迭代算法，即基于单体扩张的端元提取算法。首先，随机选取已知数目的像元作为初始端元集，用初始端元线性表示其他像元，得到一系列表示系数，确定出负系数的绝对值最大的像元，表明此像元离单体的“距离”最远，将其替换初始端元中的某一个，使得替换后的单体体积最大；重复上述过程直到无负系数。从而找到使凸面单体体积达到最大的像元集，即端元。

1 端元提取的相关理论

相关理论是基于理想情形下给出，即数据无噪声，且完全满足线性混合模型。

1.1 端元提取的理论模型

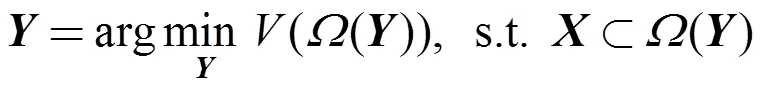
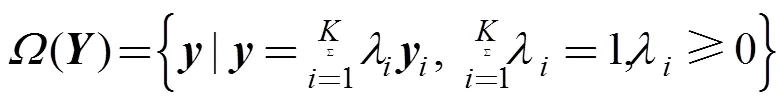
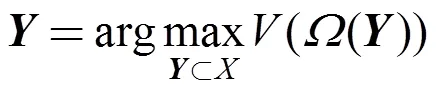
本文将基于线性混合模型展开讨论。

1.2 基于线性表示的端元判定

在中任取个无关点1,2,…,，并记＝{1,2,…,}，＝{1,2,…,}是端元集，则有以下结论。

定理1的凸面单体()中的任意向量均可被1,2,…,线性表示，且系数和为1。

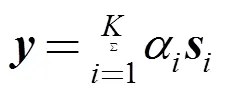
定理2的凸面单体包含于的凸面单体中，即()Ì()。

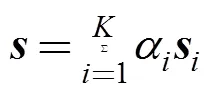
定理1表明，对任意Î，均可被唯一地线性表示，且系数之和为1，若系数全非负，则Î()，否则Ï()。定理2表明，将Î均由来线性表示，若所有的表示系数全非负，则就是端元。

定理3＝{1,2,…,}是端元集的充分必要条件是高光谱向量集被线性表示的系数均非负。

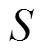
必要性，由定理1和定理2显然可得。

2 理想情形下端元提取算法

基于上章给出的理论，端元提取的实现涉及3个内容，分别是单体体积计算、线性表示的系数确定以及算法流程。

2.1 单体体积计算

根据文献[13]，以1,2,…,为顶点的－1维凸面单体的体积(())的计算公式为：

式中：＝{2－1,3－1,…,－1}。

2.2 线性表示的系数确定

若端元个数为，则在理想情形下，Ì()，高光谱向量集的秩为，由于1,2,…,线性无关，所以Î(＝1,2,…,)，均可由1,2,…,唯一地线性表示，＝{1,2,…,}其系数＝{1,2,…,}，由线性方程组确定：

＝(＝1,2,…,) (3)

2.3 端元提取算法流程

算法采用迭代思想，首先从中任意选取个无关点作为初始端元＝{1,2,…,}，再从中找出一个向量0来代替中的一个向量0，形成迭代过程。

确定0的规则是使其离单体()尽量“远”，考虑到当用1,2,…,来表示x时，其负系数的绝对值越大，表明离单体()的“距离”越远，所以可用线性表示的系数来确定0。确定被替换对象0的规则是使替换后的单体体积尽量大。具体流程如下：

输入：高光谱向量＝{1,2,…,}，端元个数；

输出：端元向量1,2,…,。

第一步：在中任取个无关点1,2,…,；

第二步：对Î，求线性方程组c＝得到系数，并记＝min(1,2,…,)(＝1, 2,…,)；

第三步：若≥0(＝1, 2,…,)，则1,2,…,是端元向量并输出，结束；

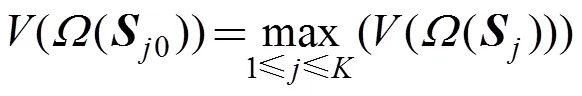
尽管未能证明算法第三步中((0))＞(())一定成立，但大量数值实验均未出现算法失效的情形。

3 非理想情形的端元提取算法

上述理论和算法均基于理想情形，而实际数据一定不是理想状况，叠加了各种噪声，理论条件均不满足，几个关键的问题及算法改进如下：

1）数据集不在同一－1维超平面内，而分布在超平面“两侧”附近，Ì()只在“距离很近”的意义下成立。

2）的秩远远大于，线性方程组(3)无解，但由于“近似”落在维超平面内，所以，可以求出线性方程组(3)的最小二乘解，作为“近似线性表示”系数。

3）由于噪声的存在，算法步骤第三步中不能保证((0))＞(())，每次迭代得到的单体体积不单调，不能保证算法收敛，出现算法失效的情况。对此，将算法第三步找出一个离()“最远”点0的步骤，嵌套入一个内层迭代，这样，算法第三步改进如下：

第三步：若≥0(＝1,2,…,)，则1,2,…,是端元向量并输出，结束；

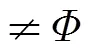
理论上，可能存在算法失效的情形，但大量数值实验均未出现失效情况。

4 实验与分析

实验首先通过人造数据，在端元已知的情况下，运用算法提取端元，再对真实高光谱数据进行实验。

4.1 仿真实验

首先针对不添加噪声的理想情形，再次针对添加噪声的非理想情形。

4.1.1 理想情形下

为验证本算法的有效性，实验首先用人工合成的三维数据，点(1,1.2,3)，(0.4,2,1)，(3,2,1)为理论端元，被随机产生的归一化的非负系数合成2000个点，即这2000个点在3个端点向量组成的三角形内，此时不添加任何的噪声。实验结果如图1所示，图中黑色部分圈出的点为提取出的“端元”，图1(a)为算法初始时随机选取的3个“端元”，图1(b)为算法经过第一次迭代，可观察到此时提取出其中的一个端元，图1(d)为算法最终迭代，提取出的端元，恰为理论端元。

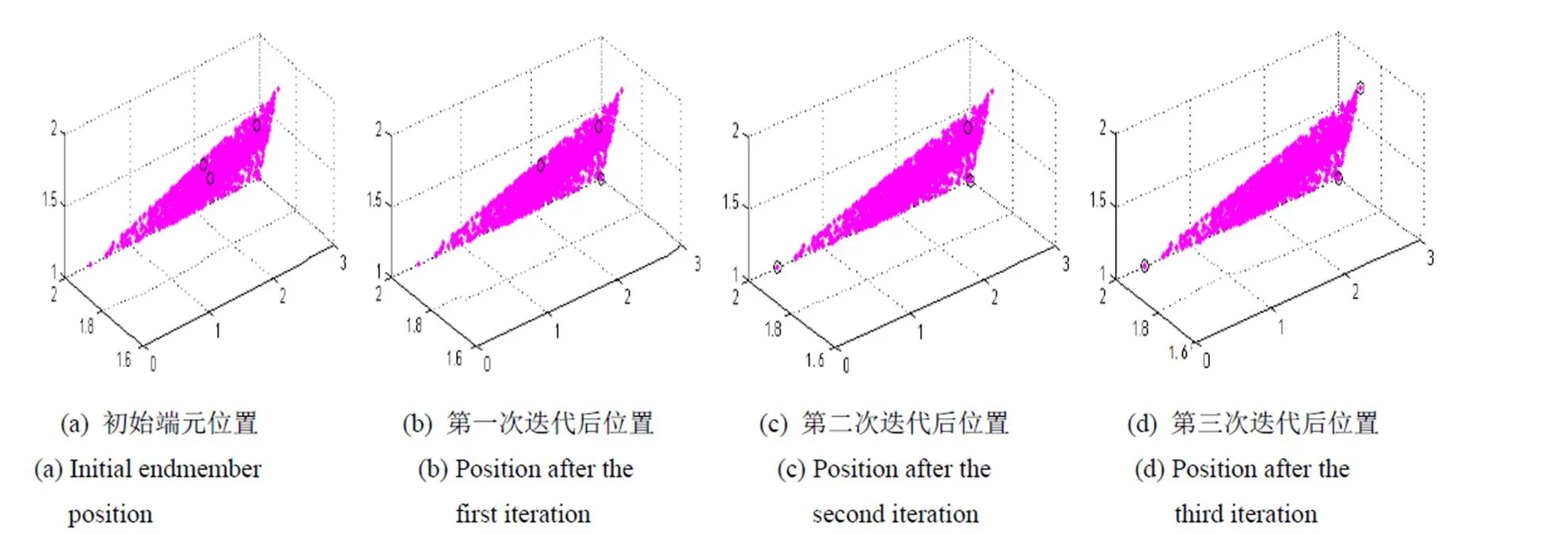
图1 理想情形下的端元提取过程图

4.1.2 非理想情形下

实验依旧用人工合成的三维数据，点(1,1.2,3)，(0.4,2,1)，(3,2,1)为理论端元，被随机产生的归一化的非负系数合成2000个点，再附加0均值的高斯噪声，实验结果如图2所示，图中黑色部分，圈出的点为提取出的“端元”，图2(a)为算法初始时随机选取的3个“端元”，图2(b)为算法第一次迭代，可观察到此时提取出其中的一个端元，图2(d)为算法最终迭代提取出的端元，恰为理论端元。计算出本算法提取的端元单体体积最大，如表1。

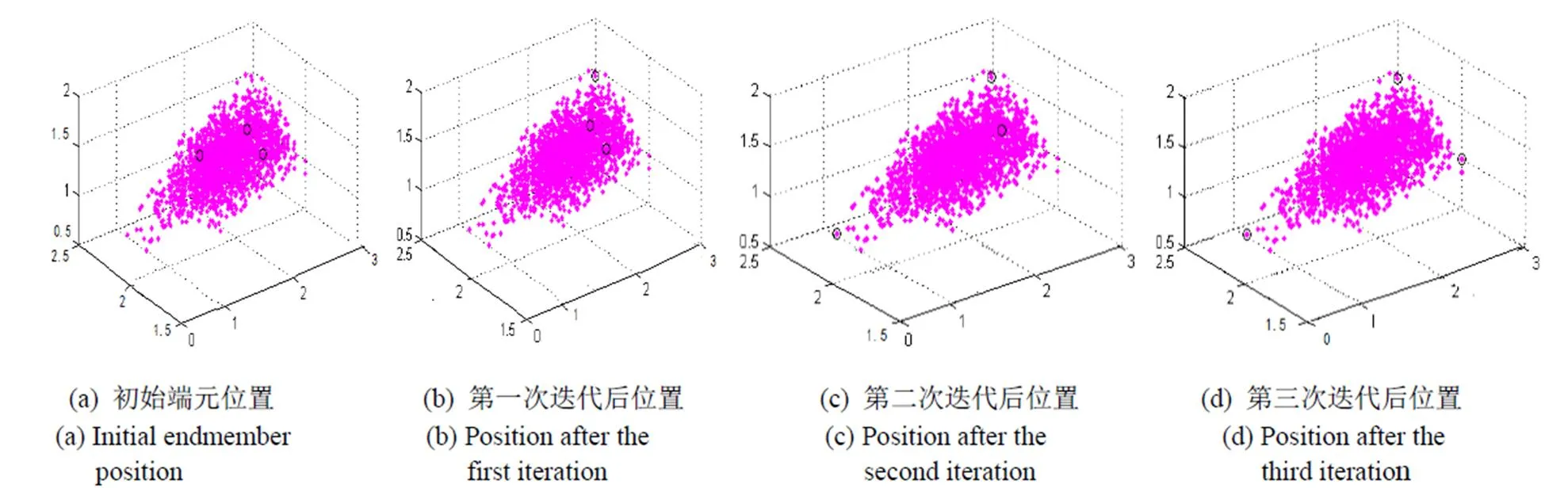
图2 非理想情形下的端元提取过程图

表1 三种算法所得端元单体的体积

当合成数据为20维，3个端元时，被随机产生归一化的非负系数合成10000个像元，分别加入信噪比为15dB，25dB，35dB，45dB，55dB的高斯白噪声时，用3种方法提取出端元，计算平均光谱角距离（mSAD）的值，得到的结果如图3(a)所示，本文算法对噪声的敏感性低。

当端元数目分别为3，4，5，6，7个时，维数为20，分别被随机产生归一化的非负系数合成10000个像元，加入信噪比为35dB的高斯白噪声，用3种算法提取端元计算提取的端元与真实端元的mSAD值，如图3(b)所示，本文算法得到mSAD值为0，说明端元提取精度最好的是本文算法，其次是VCA算法，PPI算法最差。

4.2 高光谱数据的算法实验分析

本文用美国内华达州Cuprite地区的AVIRIS数据进行分解实验，Cuprite地区AVIRIS原始数据，共224个波段，光谱分辨率为10nm，尺寸为350×350像元，删除噪声较大和光谱吸收较大的波段，本文选择172～221光谱区间的50个波段用于算法测试，已知端元数目为8[14]，算法迭代16次，便可提取出最终端元，用提取出的端元对高光谱影像进行丰度反演，反演时运用基于几何距离的全约束混合像元分解算法（DGAE）[15]，得到的丰度图如图4(a)～图4(h)所示，将各丰度图与图4(j)的调查分类结果图比较，从而确定端元对应的矿物。图4(i)为端元的位置分布。图4(k)为用于处理的区域的AVIRIS假彩色合成图像。最终将本文算法与VCA，PPI算法得到的端元体积进行比较，如表2所示，本文算法得到的体积最大。

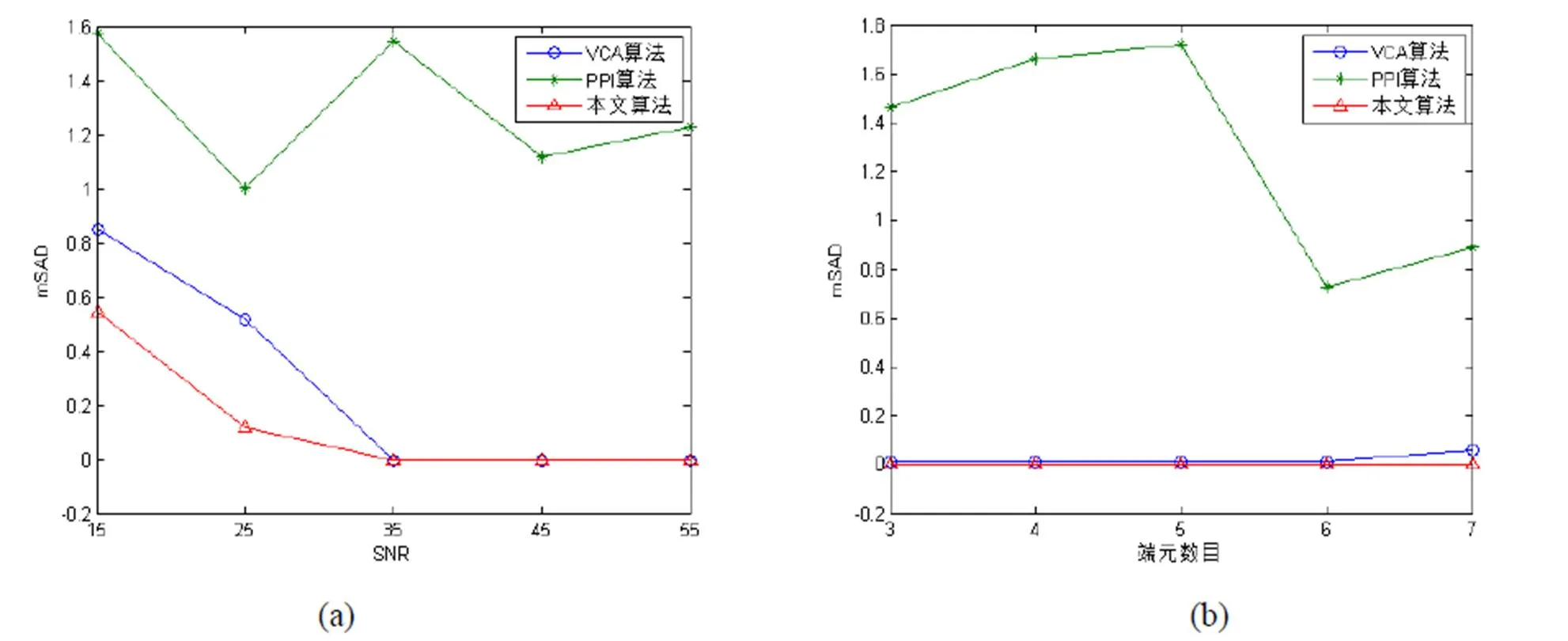
图3 3种算法性能比较

表2 3种算法所得端元单体的体积

为了进一步比较，我们将USGS库中对应的矿物光谱作为参考光谱，将参考光谱在相应的波段范围内能量求积分，转换为光谱向量，并求取解混所得的端元与它们之间的光谱角，如表3所示，可以看出，用本文方法提取的端元与USGS光谱库中的标准光谱相似度较高，总体上优于VCA与PPI算法提取的端元光谱。

5 结论

本论文是在线性混合模型的基础上，假设纯净像元存在的前提下提出的，是一种基于单体扩张的端元提取算法，它的主要思想就是基于线性表示的端元判定，给出了端元判别的定理，并将定理进行证明，是另外一种迭代算法，并且，通过迭代，优化其时间效率。文中用人工仿真的数据与真实的高光谱数据进行实验，表明本算法精度高，稳定性好。算法是在端元数目已知的情况下给出的，后续工作将针对端元数目未知时进行研究。

图4 美国Cuprite地区AVIRIS数据端元分解结果（350像元×350像元）

表3 提取的端元与标准光谱库中的标准光谱的光谱角距离

[1] 李二森, 朱述龙, 周晓明, 等. 高光谱图像端元提取算法研究进展与比较[J]. 遥感学报, 2011,15(4): 659-679.

LI Ersen, ZHU Shulong, ZHOU Xiaoming, et al. The development and comparison of endmember extraction algorithms using hyperspectral imagery[J]., 2011, 15(4): 659-679.

[2] JI Luyan, GENG Xiurui, Sun Kang, et al. Modified N-FINDR endmember extraction algorithm for remote-sensing imagery[J]., 2015, 36(8): 2148-2162.

[3] 杨可明, 魏华锋, 刘飞, 等. 以光谱信息熵改进的N-FINDR端元提取算法[J]. 地球信息科学学报, 2015, 17(8): 980-985.

YANG Keming, WEI Huafeng, LIU Fei, et al. Improved N-FINDR algorithm on hyperspectral endmember extraction based on spectral Shannon entropy[J]., 2015, 17(8): 980-985.

[4] ZHAO L, FAN M, WANG L. Fast implementation of linear and nonlinear simplex growing algorithm for hyperspectral endmember extraction[J].,2015, 126(23): 4072-4077.

[5] LIU Junmin, ZHANG Jiangshe. A new maximum simplex volume method based on householder transformation for endmember extraction[J]., 2012, 50(1): 104-111.

[6] Rob Heylen, Paul Scheunders. Multidimensional pixel purity index for convex Hull estimation and endmember extraction[J]., 2013, 51(7): 4059-4069.

[7] 徐军, 徐富红, 蔡体健, 等. 一种基于最大距离的纯像元指数端元提取算法[J].地球信息科学学报, 2015, 17(1): 86-90.

XU Jun, XU Fuhong, CAI Tijian, et al. A novel pure pixel endmember extraction algorithm based on the maximum distance[J]., 2015, 17(1): 86-90.

[8] Jose M, Rodriguez Alves, Jose M, et al. Vertex component analysis Gpu-based implementation for hyperspectral unimixing[C]//, 2012: 10.1109/WHISPERS.2012.6874337.

[9] 何晓宁, 曹建农, 高坡, 等. 基于顶点成分分析法的端元提取改进算法[J]. 测绘通报, 2013 (7): 30-34.

HE Xiaoning, CAO Jiannong, GAO Po, et al. An improved algorithm of endmember extraction based on vertex component analysis[J]., 2013(7): 30-34.

[10] John Gruninger, Anthony J Ratkowski, Michael L Hoke. The sequential maximum angle Convex Cone(SMACC) endmember model[C]//,[C]//2004, 5425: doi:10.1117/12.543794.

[11] LIU C, LI J, WANG G. Endmember extraction algorithm for hyperspectral image based on PCA-SMACC[C]//,, 2014, 9142:91421A.

[12] Ambikapathi A M, Chan T H, Ma W K. A robust alternating volume maximization algorithm for endmember extraction in hyperspectral images[C]// 2on, 2010: 10.1109/WHISPERS.2010.5594862.

[13] SUN Kang, GENG Xiurui, WANG Panshi, et al. A fast endmember extraction algorithm based on gram determinant[J].,2014, 11(6): 1124-1127.

[14] 田玉刚, 杨贵. 端元快速提取的光谱梯度特征搜索法[J]. 测绘学报, 2015, 44(2): 214-219.

TIAN Yugang, YANG Gui. A fast endmember extraction algorithmusing spectrum gradient features[J]., 2015,44(2): 214-219.

[15] PU H, XIA W, WANG B, et al. A fully constrained linear spectral unmixing algorithm based on distance geometry[J].,2014, 52(2): 1157-1176.

Endmember Extraction Algorithm Based on the Simplex Expansion

DONG Anguo，HAN Xue，GONG Wenjuan

（School of Science, Chang’an University, Xi’an 710064, China）

Endmember extraction is a key step in unmixing hyperspectral mixed pixels. In order to extract endmembers of hyperspectral image, this paper proves that if a vector in vitro and vivo is represented by a vertex vector, there will be a negative coefficient based on the theory of linear representation and the theory of convex cone model. The theory gives a necessary and sufficient condition for the endmembers identification. A new iterative algorithm is proposed under non-ideal situation. The experimental results show that the precision of the endmember extraction using the algorithm proposed in this paper is better than VCA algorithm. And this algorithm has better efficiency than the search algorithm. It has good stability and a low sensitivity to noise.

hyperspectral，convex cone，endmember extraction，simplex

TP7

A

1001-8891(2016)11-0947-06

2016-05-24；

2016-08-05.

董安国（1964-），男，浙江象山人，教授，硕士生导师，主要研究领域为数值代数，数字图像处理，E-mail：donganguo@chd.edu.cn。

国家自然科学基金项目（41571346），国家自然科学基金项目（40971217），国家自然科学基金项目（11201038）。