调速器参数对水电站水力干扰过渡过程的影响

赖 旭，陈 强

(武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

0 引 言

对于采用一洞多机布置形式的电站，由于机组运行时存在水力联系，当其中一台机组丢弃全负荷或者大幅度增加负荷时，必然对其他正常运行的机组产生影响，这种水力干扰[1-3]引起的过渡过程将直接影响电站的供电质量，严重时还将影响电站的安全稳定运行。因此，针对水电站水力干扰过渡过程的研究是十分必要的。而已有水力干扰过渡过程的研究多采用简化模型，发电机数学模型多采用简化的一阶模型，管道模型多采用弹性管道模型；只考虑引水发电管道系统和水轮机的影响，忽略了电气系统的影响。如文献[4]采用弹性管道模型及一阶发电机模型，研究了分叉管的位置和调压室面积等引水道参数对水电站水力干扰过渡过程的影响；文献[5]采用一阶发电机模型，研究了引水发电系统稳定以及调速器参数对系统稳定性的影响。以往调速器参数对电站过渡过程影响的研究多针对单管单机布置形式的电站，如文献[6,7]均在单管单机仿真模型的基础上，研究了调速器参数对单管单机水电站的小波动过程的影响。目前，针对一洞多机电站展开调速器参数对水力干扰过渡过程影响与参数优化的研究还很少。

本文采用特征线法建立管道模型及分岔管模型，并引入高阶发电机模型以及励磁系统和负载模型，建立了完整的水机电联合仿真模型，在此基础上研究了调速器参数对一洞多机布置形式的电站水力干扰过渡过程的影响，并利用多目标粒子群(MOPSO)算法对调速器参数进行了优化。

1 引水发电系统数学模型

水电站引水发电系统模型包括引水管道、水轮机、调速器、发电机、励磁系统和负载，它们之间的整体关系如图1所示。引水管道采用特征线法[8]，水轮机采用水轮机的模型综合特性曲线[9]。

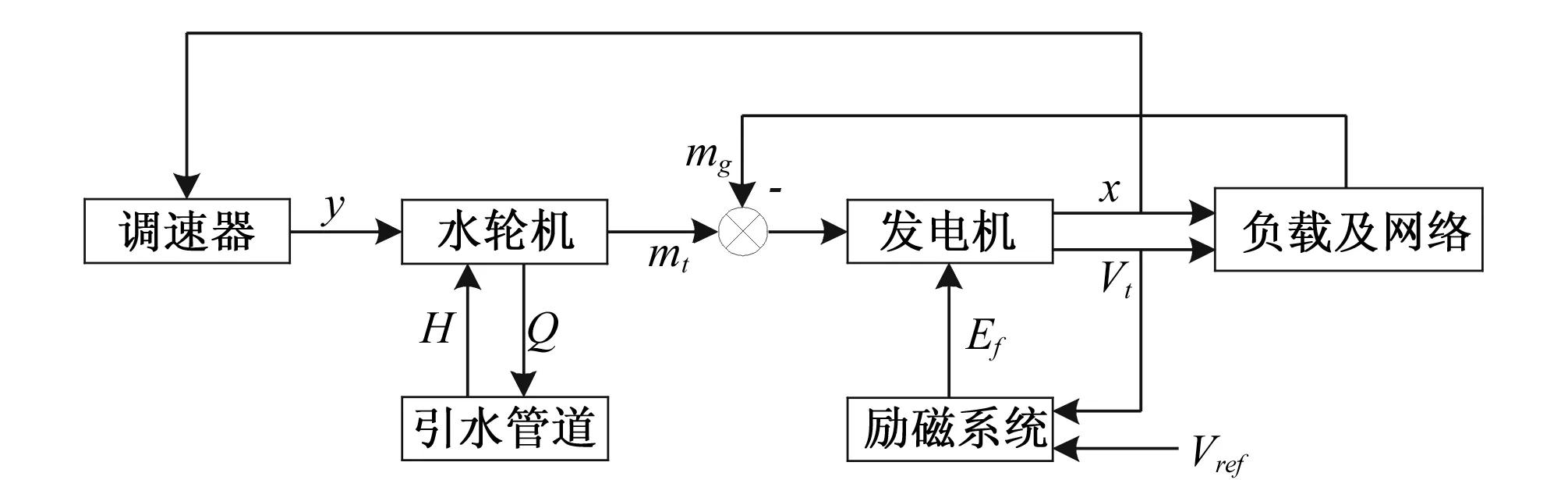
图1 水电站引水发电系统结构框图Fig.1 Structure of water diversion and power generation system in hydropower station

1.1 分岔管数学模型

对于如图2所示的分岔结点，方程组可写为[8]：

特征方程：

HA=CAP-BAQA

HB=CBM-BBQB

(1)

HC=CCM-BCQC

连续性方程：

QA=QB+QC

(2)

如果结点处的水头损失以及不同管道的流速头之差可以忽略，于是能量方程：

HA=HB=HC

(3)

联立求解式(3)至式(5)，可得：

(4)

于是，HB和HC可由式(3)确定；QA,QB和QC可由式(1)确定。

对于超过三根分岔管的分岔结点，也能得出相似的方程组。

1.2 调速器数学模型

频率调节:采用辅助接力器型调速器, 方框图如图3所示，其微分方程的表达式为[9]：

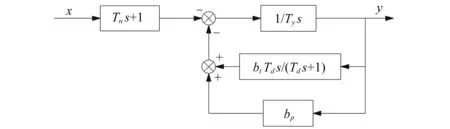
图3 辅助接力器型调速器方框图Fig.3 Block diagram of auxiliary Servomoter governor

(5)

功率调节，采用 PI 型控制模式，方框图如图4所示，其微分方程的表达式为：

图4 PI型控制模式方框图Fig.4 Block diagram of PI control mode

(6)

式中：x为机组转速偏差相对值；Pg为机组给定功率；Pt为机组实际功率；Tn为测频微分时间常数或加速时间常数；Td为缓冲时间常数；bt为暂态转差系数；bp为永态转差系数；Ty为主接力器时间常数。

1.3 发电机数学模型

在忽略定子绕组暂态，并忽略阻尼绕组的作用，只计及励磁绕组的暂态和转子动态的假设下，将转子运动方程、电流电压方程和电磁暂态过程方程联合起来得到发电机三阶数学模型[10,11]：

电磁暂态方程和定子磁链方程：

(7)

电磁转矩方程和定子电压方程：

(8)

转子运动方程：

(9)

式中：ω、δ分别为转子角速度相对值和转子电角度；ω0为转子额定角速度；Vt、I分别为发电机端电压和定子电流，下标d、q分别表示d、q轴分量；Ef为由励磁电压所决定的假想空载电势；E′q为发电机q轴暂态电势；Ta为机组惯性时间常数；T′d0为d轴暂态开路时间常数；X′d为d轴暂态电抗；Xd、Xq为发电机d、q轴同步电抗；ψd、ψq为d、q轴磁链；Me为电磁力矩；D为阻尼系数。

1.4 励磁系统模型

本文采用如图5所示的I型静止励磁系统。

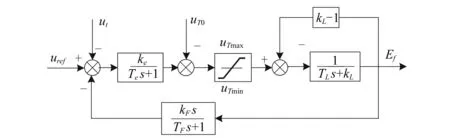
图5 励磁系统模型框图Fig.5 Block diagram of excitation system model

图5中，ke和Te分别为该惯性环节即调节器总体的放大倍数和时间常数，kL和TL分别为励磁机的自并激常数和等值时间常数，kF和TF分别为该环节额定放大倍数和时间常数。

1.5 网络数学模型

网络元件主要包括输电线路，本文采用电力系统分析中常用的输电线路集中参数元件模型中的∏型等值电路。在电力系统稳定分析中，电力网络一般采用稳态方程来代表。同时，假定正常运行时三相是对称平衡的，故可以用单相系统来表示。

设线路阻抗(包括输电线路和变压器)为Z=Re+jXe，则有：

ΔV=IZ

若用d-q坐标系表示，则得到：

(10)

式中：i表示送端节点；j表示受端节点。

对于无穷大电网，设电网电压为Us,则：

(11)

1.6 负荷数学模型

本文采用恒定阻抗法，即根据正常运行方式下负荷点的电压VH0和功率SH0=PH0+jQH0,用下式求出负荷的阻抗值：

(12)

并假定暂态过程中该阻抗值不变。

2 算例分析

由以上给出的引水发电系统各环节的数学模型，按照水电机组控制系统各个环节的连接关系进行连接，建立包含水力、机械和电气各子系统的水电站水机电联合仿真计算模型。

如图6所示，某电站布置形式为一洞两机，具体参数如下：水轮机：nr=428.6 r/min，Pr=45.36 MW，Qr=31.48 m3/s，Hr=154.3 m；

引水管道：L=850 m，A=25.13 m2，l1=l2=50 m，A1=A2=12.56 m2，a=1 000 m/s；

发电机：Xd=1.07 pu，X′d=0.38 pu，Xq=0.66 pu，T′d0=5.4 s，cosφ=0.8，Ta=9.098 s，en=0，un=10.5 kV。

励磁系统：ke=50，Te=0.08 s，kL=1，TL=1.06 s，kF=0.04 s，TF=0.04 s。

调速器：Ty=0.4 s，频率调节：bp=0，功率调节：bp=0.04。

网络：Xe=0.2 pu，Re=0。

负荷：PH0=1，QH0=0.01，VH0=1。

水电机组采用上述参数，水电站系统初始处于额定运行状态，水力干扰的过程：1号机正常运行，2号机组甩负荷，导叶10 s直线关闭。

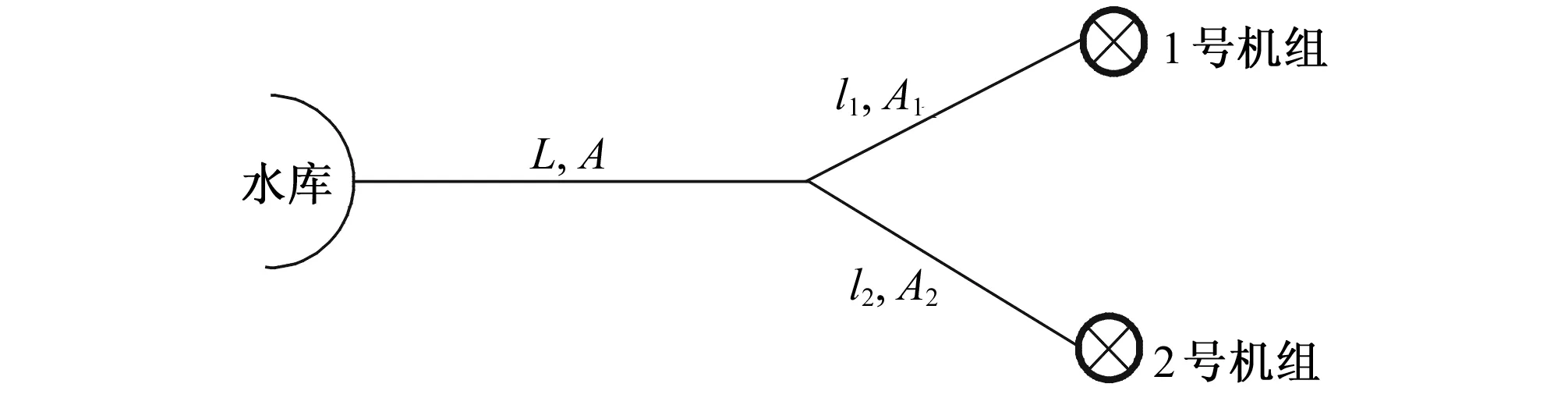
图6 一洞两机电站示意图Fig.6 Diagram of single-pipe two-units hydropower plant

2.1 调速器参数对水力干扰过程的影响

根据《水轮机电液调节系统及装置技术规程》[12]，调速器主要调节参数及其调整范围为：暂态转差系数bt(1%～200%)，缓冲时间常数Td(1～20 s)和加速时间常数Tn(0～2 s)，以下仿真计算中各参数均位于调整范围内。

2.1.1机组并无穷大电网

机组并无穷大电网，采用频率调节，因转速恒定，则调速器不动作；采用功率调节，调速器动作以跟踪给定功率，减小差值。发生水力干扰时，机组采用频率调节和功率调节的结果对比如图7所示。

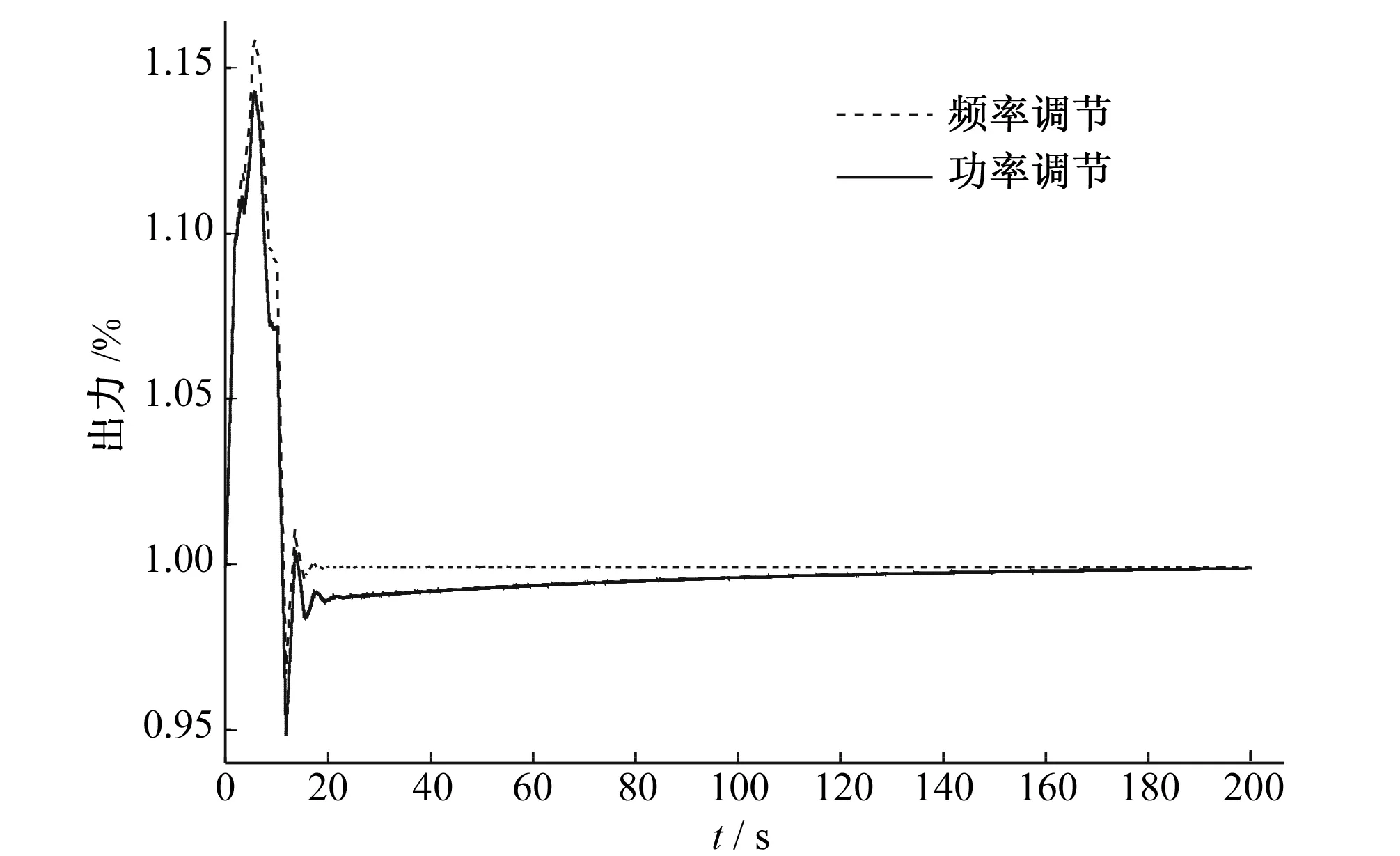
图7 频率调节与功率调节机组出力结果对比(bt=0.5,Td=8)Fig.7 Comparison results of Output between frequency regulation mode and power regulation mode(bt=0.5,Td=8)

由结果对比图可知，频率调节相比功率调节，机组出力波动幅值较大。其原因在于，水力干扰过渡过程中机组实际功率发生改变，功率调节模式下调速器动作以减小与给定功率的差值，从而减小了出力波动幅度；而频率调节模式下，调速器对水力干扰过渡过程不做调节，机组出力波动幅度较大。因此，机组并无穷大电网，发生水力干扰应采用功率调节。

针对上述实例，对功率调节模式下调速器参数做仿真比较，结果如图8所示。

由图8可知，暂态转差系数bt越小，机组出力波动幅值越小，但减小幅度有限；缓冲时间常数Td的不同取值所得出力结果基本重合，对机组出力几乎没有影响。因此，机组并无穷大电网，调速器参数取值的不同对水力干扰过渡过程影响较小。

2.1.2机组并孤立电网

机组并孤立电网，通常采用频率调节模式。水力干扰过渡过程中调速器参数按小波动整定原则确定，可以保证系统稳定[5]。因此采用传统的斯坦因推荐公式整定调速器参数作为典型参数[9]:

bt=1.5Tw/Ta=0.245 5

Td=3Tw=4.467

Tn=0.5Tw=0.744 5

对上述实例做仿真比较，结果如图9所示。

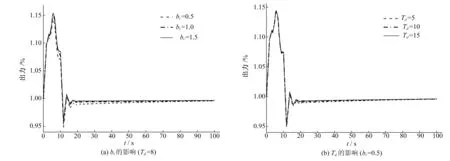
图8 无穷大电网条件下调速器参数对水力干扰过程的影响Fig.8 Effect of governor parameters on the process of hydraulic disturbance on the condition of infinite power grid

图9 孤立电网条件下调速器参数对水力干扰过程的影响Fig.9 Effect of governor parameters on the process of hydraulic disturbance on the condition of isolate power grid

相比简化模型仅能反映流量、压力等水力系统物理量的动态过程，完整的水机电联合仿真模型计算还能得出电气侧的各物理量的变化过程，如机组电流的动态过程。对比图9中机组出力、转速与电流动态响应可见，机组电流变化过程与机组出力、转速变化过程基本一致，但响应速度更快，波动更明显。

由图9(a)可知，暂态转差系数bt越大，机组出力、转速及电流的超调量越大，衰减也越慢；对比图9(b)、图9(c)可知，相比Td和Tn，改变bt的大小对水力干扰过渡过程的影响更为显著。

由图9(b)可知，缓冲时间常数Td越大，机组出力、转速及电流的超调量越大，但衰减较快；改变Td的大小对超调几乎没有影响，对后续衰减影响较大。

由图9(c)可知，加速时间常数Tn越大，机组出力、转速及电流的超调量越小，衰减越快；可见Tn取值的增大有利于水力干扰过渡过程中各物理量的调节。

综上所述，机组并孤立电网，调速器参数取值的不同对水力干扰过渡过程影响较大，其中以bt影响最为显著。

2.2 调速器参数的优化

机组并无穷大电网，调速器参数对水力干扰过渡过程影响较小。而机组并孤立电网，调速器参数对水力干扰过渡过程影响较大，因此本文主要研究机组并孤立电网调速器参数的优化。

Coello等提出了基于动态网格归档技术的多目标粒子群[13](multi-objective particle swarm optimization，MOPSO)算法，并做了实例验证，结果表明了算法的有效性。本文根据其算法编制程序。

MOPSO算法的参数设置如下：

(1)基本参数：惯性因子ω=0.729，加速因子c1=c2=1.495，外部档案规模为100，种群粒子数为30，最大迭代次数为50。

(2)寻优参数：水轮机调速器需要优化的参数有3个：暂态转差系数bt，缓冲时间常数Td，加速度时间常数Tn。

(3)性能指标函数(目标向量)：性能指标函数用以评价群体中每个粒子的性能，就本文而言，优化PID参数的目标就是使得水力干扰过程中反映机组出力动态品质的超调量mp最小和调节时间ts最短；为保证系统最终稳定与机组出力最终收敛，加入第3个性能指标稳态误差e。上述3个性能指标函数构成粒子的目标向量。

针对上述实例的水力干扰过程，运用MOPSO算法对调速器参数进行优化，从MOPSO算法的最优解集中选取超调量较小、调节时间较短的折衷解，与采用典型参数对比仿真结果如图10所示，结果对比如表1所示。分析优化结果可得：

由图10可知，MOPSO折衷解所得出力结果相对典型参数不仅超调量较小，振荡幅度较小，且衰减较快。具体而言，由表1可得，MOPSO折衷解所得出力结果相比典型参数超调量减少了0.6%，调节时间减少了18.47 s。因此运用MOPSO算法获得的寻优参数得到的出力结果超调量更小、调节时间更短、动态品质优异。

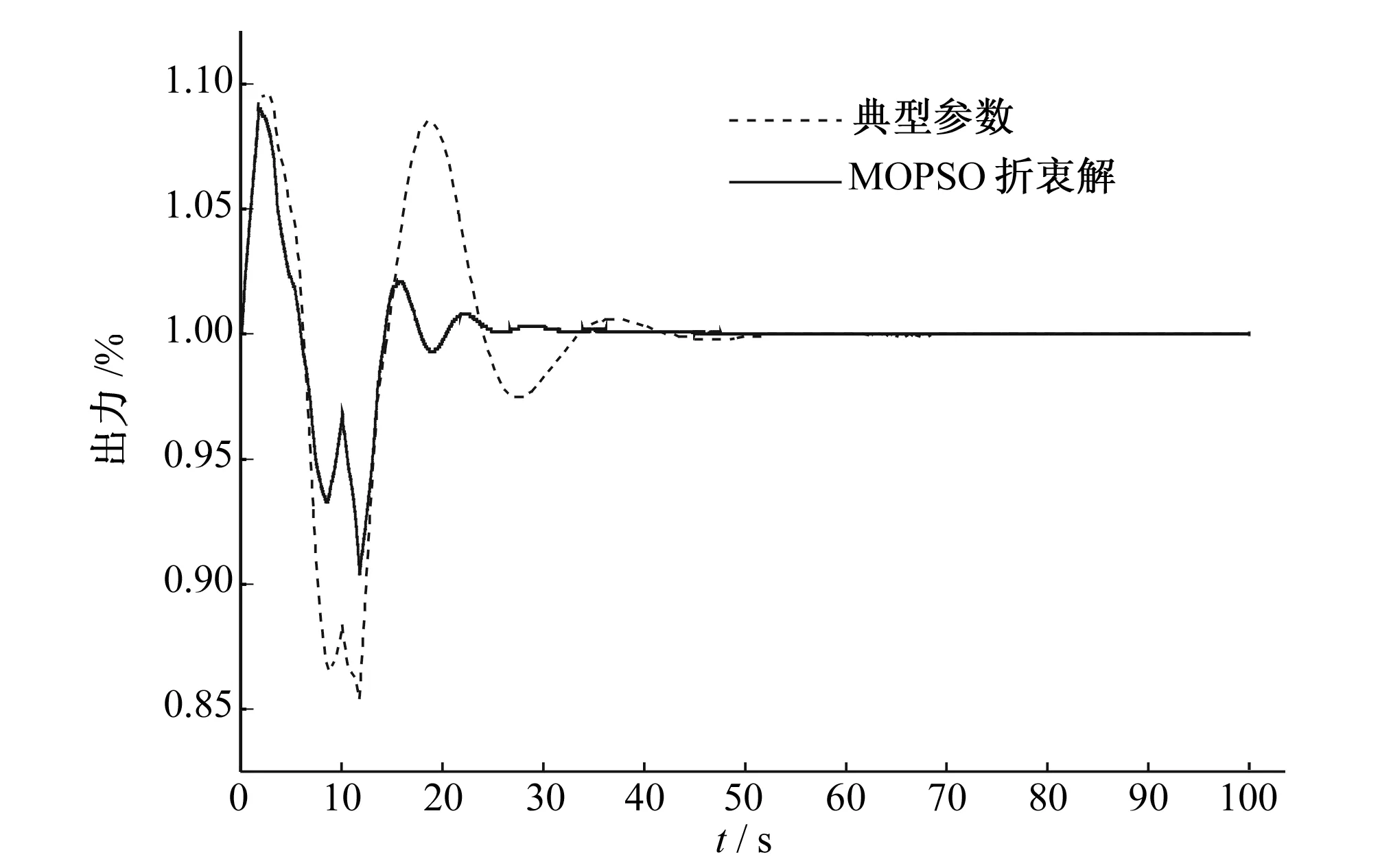
图10 两组调速器参数出力结果对比Fig.10 Output response of two sets of governor of optimal solution set parameters

3 结 语

本文在建立完整水机电联合模型的基础上，以一洞两机电站为例，对复杂引水管道系统中的水力干扰过程进行仿真，研究了调速器参数对水力干扰过渡过程的影响，并运用MOPSO算法对水力干扰过渡过程中的调速器参数进行了优化。研究结果表明：

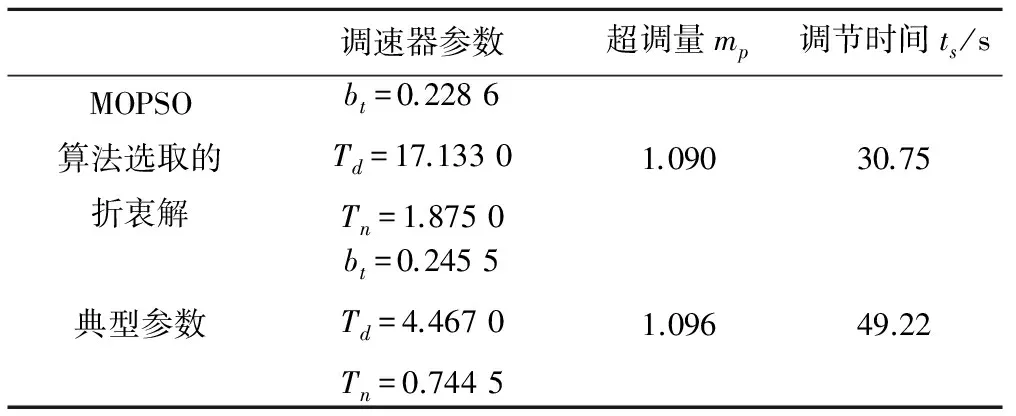
表1 MOPSO算法折衷解与典型参数结果对比Tab.1 Results of MOPSO algorithm's Compromise solution and typical parameter

(1)机组并无穷大电网，采用功率调节相比频率调节出力波动幅值较小，但调速器参数对水力干扰过渡过程的影响较小。

(2)机组并孤立电网，调速器参数对电站水力干扰过渡过程的影响较大，其中以暂态转差系数bt的影响最为显著。相比以往的简化模型，本文的水机电联合仿真模型能更精细模拟一洞多机布置形式电站的水力干扰过渡过程。

(3)以机组出力超调量mp最小、调节时间ts最短和稳态误差e最小为目标，运用MOPSO算法优化了孤网运行条件下一洞多机布置形式电站的调速器参数，优化后的调速器参数能使电站机组的出力获得优良的动态品质，改善了一洞多机布置形式电站水力干扰过渡过程，提高了电站的供电质量。

□

[1] 孔庆蓉，张永良，江春波．锦屏二级水电站长引水隧洞水力特性研究[J]．水力发电，2009，35(3)：32-37．

[2] 吴世勇，周济芳，申满斌．锦屏二级水电站复杂超长引水发电系统水力过渡过程复核计算研究[J]．水力发电学报，2015，34(1)：107-116．

[3] 王洪亮，俞晓东，陈 胜，等．吉林台二级水电站水力干扰过渡过程研究[J]．水电能源科学，2009，27(5)：169-171．

[4] 孙美凤，陆桂明．高水头引水式水电站机组之间水力干扰的研究[J]．中国农村水利水电，2002，(9)：55-58．

[5] 陈乃祥，张扬军，屠明奇，等．抽水蓄能电站中水力干扰下的过渡过程及其稳定问题的研究[J]．水利学报，1996，(10)：68-74．

[6] 孟安波，叶鲁卿，殷 豪，等．遗传算法在水电机组调速器PID参数优化中的应用[J]．控制理论与应用，2004，21(3)：398-404．

[7] 唐正茂，马士虎，解 德．基于外部存档的并行遗传算法在水轮机调速器参数优化中的应用[J]．中国电机工程学报，2012，32(28)：90-96．

[8] Wylie E B, Streeter V L. Fluid Transients in Systems[M]. Englewood Cliffs, NJ; Prentice Hall, 1993.

[9] 沈祖诒．水轮机调节[M]．北京：中国水利水电出版社，1981．

[10] 高慧敏，刘宪林．基于详细水机电模型的水电系统动态过程仿真[J]．系统仿真学报，2003，15(4)：465-471．

[11] 邹 金，赖 旭，宗 欣．发电机电磁过程对带孤立负荷运行的水电站过渡过程的影响[J]．武汉大学学报(工学版)，2013，46(1)：109-112．

[12] DL/T 563-2004，水轮机电液调节系统及装置技术规程[S]．

[13] Coello C A C，Pulido G T，Lechuga M S．Handling multiple objectives with particle swarm optimization[J]．IEEE Transactions on Evolutionary Computation，2004，8(3)：256-279．