预测-综合指标评价模型在河流健康评价中的应用----以江苏省骨干河流健康评价为例

徐 昕，陈青生，董 壮，贾东远

(1．河海大学水利水电学院，南京 210098；2.教育部陆地-水域交界带仿真实验室，南京 210098)

0 引 言

河流生态系统是指河流水体的生态系统，是陆地与海洋联系的纽带，在生物圈的物质循环中起着重要作用。近年来大量水利工程的建设，严重影响着天然河流的水文地貌条件，并对河流及其周边生态环境造成巨大影响，随着生活条件的不断改善和对河流健康重要性认识的提高，人们对河流综合功能的实现提出了越来越高的要求，为了实现经济社会可持续发展、人与自然和谐共处，以及充分发挥河流的生态、经济、娱乐等价值，研究如何对河流健康进行评价具有重要的理论和现实意义。

当前河流健康的研究工作主要着眼于评价方法的研究。众多研究人员提出制定评价准则和标准的迫切性，以开展河流健康的评价工作，遗憾的是至今还没有对评价标准和评价方法有一个理想的、统一的共识[1]，其中评价方法大致分成两个方面，一方面分类依据主要体现在人的主观能动性和客观事实性，即主观分析法和客观分析法，主观分析法主要包括：层次分析法、理性区间法、模糊层次分析法等，客观分析法主要包括：熵值法、主成分分析法、人工神经网络算法等；另一方面主要体现在评价原理的不同，即预测模型法和多指标综合评价法；预测模型法主要对在原始资料缺失的情况下对河流的健康体系进行预测评价，代表性的是神经网络算法；多指标综合评价法即综合评价，多采用层次分析、模糊层次分析法、德尔菲法等。由于神经网络算法可以最大程度地挖掘和探索原始数据信息，鉴于河流健康评价的复杂性和广泛性，可以掌握和利用的原始数据毕竟有限，神经网络算法采用内插法构造网络训练样本，将河流健康分级评价标准值作为“预测”样本进行“预测”，对已有的原始数据作为训练的样本进行多次训练，以此寻求原始数据中隐藏的各评价因子的贡献度大小，通过对与河流健康相关的多个单一指标的原始数据进行收敛计算，即可输出河流总体健康的评价数值。训练函数对数据具有一定的敏感性和记忆性，通过训练后获得训练函数，在取得其他河流的实际原始数据后，即可代入趋于稳定后的训练函数，以此对江苏省整体河流的健康状况进行预测评价，但是神经网络算法会出现不稳定性，并且当前用于预测的神经网络函数较多，无法真正辨别适应于江苏省河流健康的训练函数。多指标综合评价通过综合分析，依据专家咨询意见确立评价指标权重，计算过程简便且稳定，但是不同于预测模型法的是，多指标综合评价方法由于人的主观臆断性易产生系统偏差。本文尝试结合预测模型法和多指标综合评价法，提出了预测-综合指标评价模型，此评价模型由3种预测模型和3种多指标综合评价方法组成，即先应用此模型对具有流域代表性的部分骨干河流的健康进行探索性评价，通过比对预测模型法和多指标综合评价的结果，选取与多指标综合评价结果相似度最高的预测函数作为最适用于江苏省河流的预测训练函数，最后应用此精简后的模型对江苏省整体河流的健康状况进行评价和预测，并取得了良好的效果。

1 江苏省河流健康评价模型

江苏境内河流纵横，湖泊众多，其中主要河流727条，大于0.5 km2的湖泊共计137个，水域面积占全省国土面积的16.91%。得天独厚的江河湖泊资源，是江苏最大的自然资源和发展优势[2]。随着城镇化、工业化进程的快速推进，河流生态环境问题日趋突出，尤其是太湖蓝藻集中爆发而引发的无锡供水危机，深刻地警示我们，加强河湖管理，维护河湖健康生命，保障水资源可持续利用，俨然已经成为全社会一项重要而又紧迫的任务。

根据《湖泊健康评估指标、标准与方法(试点工作用)》、《环境影响评价技术导则与标准》等已有的国家、行业、地方或国际标准，首先应构建河流健康评价指标体系，鉴于河流健康评价的多样性与复杂性，利用层次分析建立梯级层次结构评价指标体系，如表1，目标层为江苏省河流健康评价，准则层分为自然属性和社会效益两个方面，指标层包含11个详细指标：河岸带状况(RS)、河流连通阻隔(RFC)、生态流量满足程度(EF)、河流水质综合指数(WQ)、岸坡植被结构完整性(SVS)、河流生物多样性(AL)、防洪工程达标率(FLD)、岸线利用管理(SUM)、公众满意度(PP)、供水水量保证率(WSG)、水功能区水质达标率(WFZ)，各指标分别反映河流多层次和深层次的作用效益。

表1 江苏省河流健康评价体系Tab.1 River Health Assessment System in Jiangsu Province

2 预测-综合指标评价方法简介

鉴于当前越来越繁多的评价方法，可能导致河流健康评价出现“多端寡要、好谋无决”的分极现象，所以研究出一种或者多种准确而客观的方法系统越来越显示其重要性和迫切性。尽管神经网络算法受评价指标的标准取值和上下限值的影响，会出现不稳定性，但可以最大限度地克服人的主观性；综合指标评价方法的优点在于计算过程非常稳定，但河流健康评价因“河”而异、因“时”而异[3]，综合指标评价法在不同河流的不同时段，均需依赖于专家的问卷意见，存在一定的主观性和局限性。预测-综合指标评价模型融合了神经网络算法和综合指标评价法的各自优势，即配置综合指标评价模型的校验，预测模型会逐步趋向稳定；存在预测模型的计算，综合指标评价模型会更为客观准确。

在预测模型上选用BP神经网络、径向基神经网络(RBF)、广义回归神经网络(GRNN)3类神经元算法；在综合指标评价模型上选用层次分析法(AHP)、网络分析法(ANP)、模糊层次分析法(F-AHP)3类，模型运行过程如图1所示，即先用3种神经网络算法对河流健康进行初步评价，选取最合适该流域健康的预测评价模型，然后使用3种综合指标评价方法进行校验，两者结论进行比较，留用与综合指标评价方法数值相接近的算法，作为该流域或者区域的预测评价模型，最后对总体以及全部河流进行整体评价。这样就可以最大限度地发挥预测模型的灵活性和通用性，与流域的基本特点和变化规律有很大程度的吻合。

图1 预测-综合指标评价模型流程图Fig.1 Prediction - Comprehensive index assessment model flowchart

由于前人对层次分析法和BP神经网络算法已有较为详尽的研究，本文仅对其余4种子方法进行简要介绍。

2.1 径向基函数神经网络(RBF)

RBF神经网络又称为径向基函数神经网络，是一类常用的三层前馈网络，多用于函数逼近及分类[4]，常用的RBF网络为n-h-m结构，即网络具有n次输入(输入层)，h个隐节点(隐藏层)，m次输出(输出层)，计算的模型如图2所示。

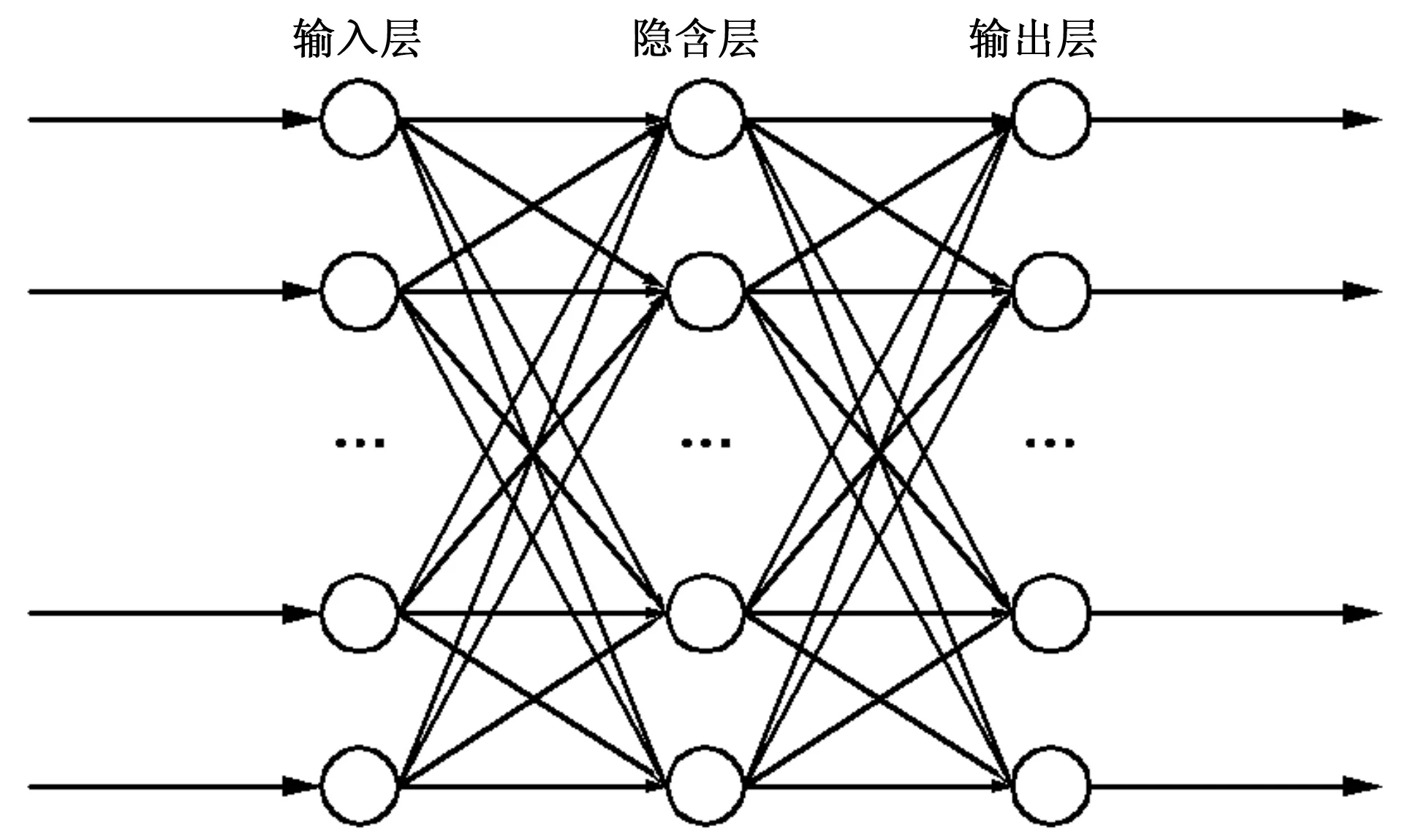
图2 径向基神经网络模型结构Fig.2 The structure diagram of RBF

2.2 广义回归神经网络(GRNN)

广义回归线性网络(General regression neural network，GRNN)是由德国人Donald Specht于1991年首先提出的新型神经网络算法[5]，由输入层、模式层、求和层及输出层4个层次网络组成计算模型如图3所示。

GRNN的主要优势在于学习迅速，在样本数量巨大的时候达到快速逼近，尤其在处理实时环境下的稀疏数据效果显著。当前，该神经网络在系统辨识和预测控制等方面得到了尝试性的应用。GRNN神经网络的创建需要将所有数据划分为输入向量、输出向量、训练数据和测试数据[6]。

图3 广义回归神经网络模型结构Fig.3 The structure diagram of GRNN

2.3 模糊层次分析法(F-AHP)

荷兰学者VanLaarhoven WP在1983年首次将模糊数学应用与层次分析法相结合，提出了模糊层次分析法[7]，集层次结构、模糊数学、权衡比较于一体，在科学决策问题上卓有成效。

2.4 网络分析法(ANP)

ANP(Analytic Network Process)，又称网络层次分析法，是Satty T.L.教授于1994年提出的，基于层次分析法(Analytic Hierarchy Process，AHP)发展而成的一种应用系统分析全面解决问题的方法[8]。ANP应用网络结构替代层次结构，充分考虑各因素之间的相互影响和依存关系，与系统工程和科学决策的问题特点相符，所以ANP具有越来越广阔的前景。

3 方法应用

本文首先评价江苏省16条骨干河流的健康状况，即中运河、里运河、通榆河、苏北灌溉总渠、大沙河、北六塘河、新洋港、长江干流、新通扬运河、秦淮河、句容河、九圩港、江南运河、望虞河、张家港、大滆运河(按排序先后进行计算)，作为参比。

对于预测模型法，本文首先将评价指标进行标准化，令数据处于[0～1]范围内，利于神经网络对数据的快速学习，以每一指标的极限值插值得到100个训练样本，在每次进行评价之前，均进行3 000次学习训练，训练结束后，再导入河流健康指标的实际值进行模拟，即可使训练函数对江苏省骨干河流的原始数据存在一定的敏感性和记忆性，得出评价结论。

对于多指标综合评价方法，本文首先建立相应的层次结构和网络结构，AHP和F-AHP均通过MATLAB程序实现[9,10]，而ANP则借助超级决策软件[11](Super Decisions)实现。综合两者评价结果形成比对表2。

表2 江苏省骨干河流评价分值比对表Tab.2 The comparison chart of Backbone rivers evaluation scores in Jiangsu Province

预测模型法与综合指标评价法对应的评价分值比对图如图4所示。

图4 各研究子方法对应的评价分值比对图Fig.4 The comparison figure each evaluation methods corresponding score

由图4可知在多指标综合评价模型的3类方法中，ANP和F-AHP的分值接近，AHP的分值误差过大，故采用ANP和F-AHP的分值作为校验标准，与预测模型法进行比较，通过比对分值，BP算法与多指标综合评价方法的整体结论相差甚远，而 RBF和GRNN算法与F-AHP和ANP的评价分值相近，故采用RBF和GRNN算法均可作为江苏省河流健康的预测模型，由此，精简后的模型由RBF、GRNN、F-AHP及ANP4类子方法组成，F-AHP和ANP作为校核标准方法，而RBF和GRNN作为计算标准，需要注意的是，在开始进行其他河流的评价前，必须对RBF和GRNN进行学习训练，使预测模型趋于稳定。秦淮河和张家港处于“不健康”水平，枝源派本，秦淮河大部分在南京市境内，是南京市最大的地区性河流，随着城市规模和逐步扩大，人类活动严重影响着天然河流的水文地貌条件，并对河流及其周边生态环境造成巨大影响，水域面积和城市周边绿地覆盖率逐年减少，导致河流健康水平严重恶化；张家港的主要河流功能为排涝、供水以及航运，存在的主要问题为水功能区水质达标率和岸坡硬质化程度高。但总体而言，江苏省骨干河流的健康状况较为良好。

4 江苏省河流健康状况

河流健康评价采用分级评分法，划分等级标准，河流健康初步分为4级，即：健康、亚健康、不健康及病态。河流健康等级如表3。

表3 河流健康评估分级表Tab.3 River Health Assessment Scale (INES)

通过对上文所述的骨干河流建立的训练函数，并查阅大量文献，缺漏或者无法确立的评价指标值通过变化特征插值来获取统计，再将RBF和GRNN预测模型应用于整个江苏省其他河流的健康评价，并取得了良好的效果，证明预测-综合指标评价具有很强的实用性和准确性。

江苏省整体河流健康状况分布情况如图5所示。

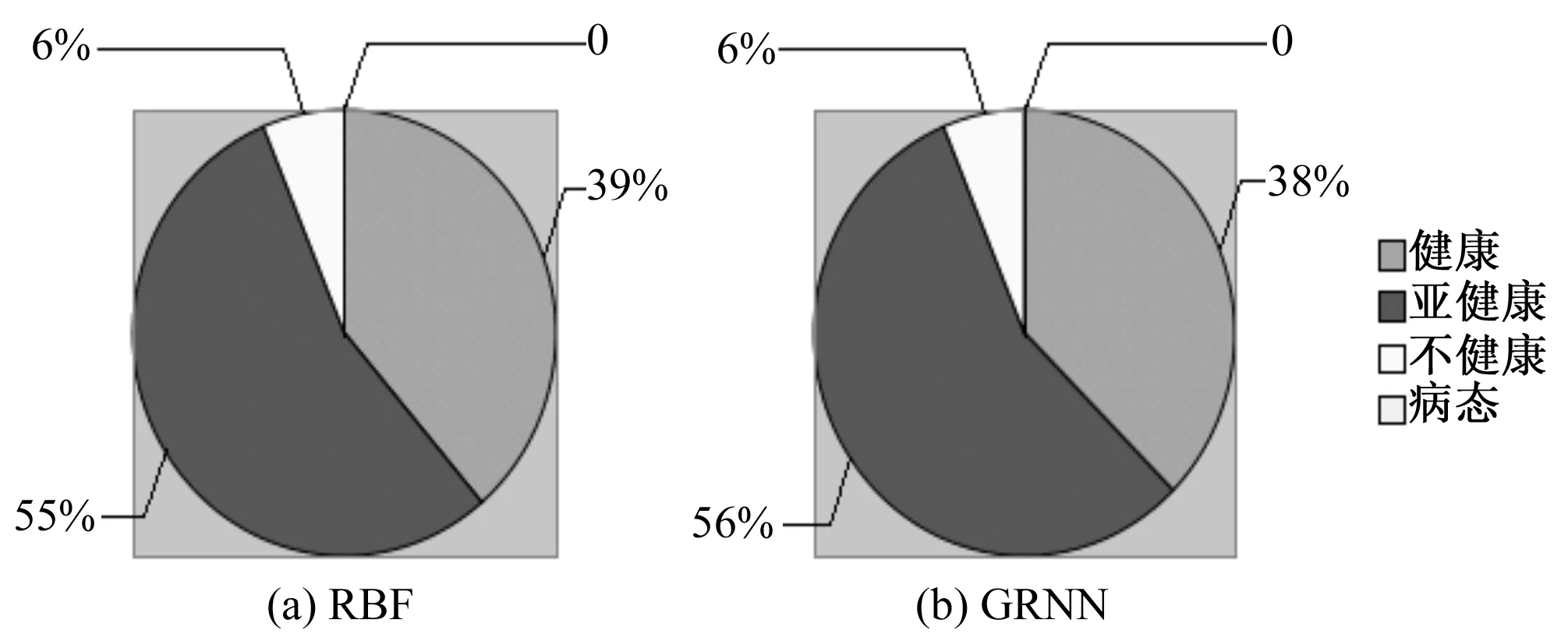
图5 江苏省整体河流健康状况分布图Fig.5 The health of the whole river in Jiangsu Province Distribution

以GRNN为例，所得结果显示，江苏省整体河流健康状况达到“健康”级别的河流占38%，达到“亚健康”级别的河流占56%，“不健康”级别的河流占6%，总体上江苏省河流处于“亚健康”(Ⅱ等)及以上状态，“亚健康”状态属于“健康”和“不健康”的过渡状态，过渡状况下的河流的健康变化显著、转变敏感，在此时期，加强河湖管理、维护河湖健康生命显得尤为重要。

5 结论与展望

(1)本文提出预测-综合指标评价模型，分别将F-AHP、ANP、AHP、BP、RBF、GRNN共6种方法作为其构成要素。首先对江苏境内16条骨干河流的健康进行了探索性评价，通过分值比对、优胜劣汰，选用 F-AHP、ANP、RBF、GRNN这4种方法纳入预测-综合指标评价体系来评价江苏省整体河流的健康状况，结果与实际情况较为接近；而AHP和BP的评价分数与其他4种方法相比相差过大，不能准确地评价河流健康，建议在江苏省河流健康评价系统中予以淘汰。

(2)从评价方法上看，基于预测模型法的RBF和GRNN神经网络评价结论几乎一致，说明两种神经网络算法均可用于江苏省河流健康评价，进行河流健康预测的目的在于克服资料缺失和人为主观性，只要取得通过训练后趋于稳定的训练预测函数，并存在和部分存在其他河流的健康评价指标原始值，通过代入即可对其他整体河流健康状况进行预测。尤其是在以后江苏省内中小河流评价可以以此作为预测评价模型，建立预警系统。尽管较多研究成果提出GRNN神经网络具有收敛速度快、预测精度高和鲁棒性良好等优点，但河流健康评价应当同时考虑地方经济发展水平的差异、流域自然环境的特点以及季节气候的变换，因地制宜地选取河流生态修复评价的标准以及权重，即河流生态修复评价应因“河”而异、因“时”而异，所以寻求最适用于江苏省河流及流域特点的预测模型也是关键性的因素，由此可知，通过多指标综合评价的结论来筛选和检验预测评价方法的适用性和准确性具有重要的理论和现实意义。

预测-综合指标评价最大程度上克服了人的主观臆断性，并可以准确而客观地预测河流健康状况，不失为河流健康评价的一类新方法。在以后的研究，应尝试将更多方法持续纳入预测-综合指标评价模型中，以提升模型的适用性和灵活性。鉴于江苏省整体河流健康状况不容乐观，因此加强河流管理至关重要，维护河流青春活力刻不容缓。

□

[1] 吴阿娜，车 越，徐启新，等.上海地区河流健康评价方法探讨[J].生态与农村环境学报，2007,23(4)：90-94.

[2] 江苏省主要河流健康状况报告[R].2012.

[3] 孙雪岚，胡春宏.关于河流健康内涵与评价方法的综合评述[J].泥沙研究,2007，(5)：74-80.

[4] 乔俊飞，韩红桂.RBF神经网络的结构动态优化设计[J].自动化学报，2010,36(6)：865-872.

[5] 崔东文.RBF与GRNN神经网络模型在河流健康评价中的应用----以文山州区域中小河流健康评价为例[J].中国农村水利水电，2012,(3)：56-61.

[6] 张娅莉,喇果彦. GRNN神经网络在信息分析预测中的应用[J].数据采集与处理，2009,24(10)：100-103.

[7] P J M Van Laarhoven WP. A fuzzy extension of Satty's priority theory[J].Fuzzy Sets and Systems.1983,3(11)：199-227.

[8] Satty T L. Fundamentals of decision marking and priority theory with the analytic hierarchy process[M]. Princeton:RWS Publications,1994:35-127.

[9] 张德丰.MATLAB神经网络应用设计[M].北京：机械工业出版社，2009.

[10] MATLAB中文论坛.MATLAB神经网络30个案例分析[M].北京：北京航空航天大学出版社，2010.

[11] 周振民，刘海滢，张 青.基于ANP的河流健康评估指标体系研究[J].中国农村水利水电，2011，(9)：57-60.