基于OMP算法五维数据规则化技术

崔永福, 苗　 青， 党青宁， 吴国忱， 裴广平， 袁　源

(1．中国石油大学　地球科学与技术学院，青岛　266580；

2．中国石油塔里木油田分公司　勘探开发研究院，库尔勒　841000)



基于OMP算法五维数据规则化技术

崔永福1,2, 苗 青2， 党青宁2， 吴国忱1， 裴广平2， 袁源2

(1．中国石油大学地球科学与技术学院，青岛266580；

2．中国石油塔里木油田分公司勘探开发研究院，库尔勒841000)

摘要：数据规则化技术是地震资料处理中的重要技术，它对改善地震数据的面元属性、提高地震资料的信噪比和成像质量有很大的优势。基于OMP算法五维数据规则化技术能综合利用三维地震数据的“纵向、横向、时间、偏移距、方位角”五个维度的信息，利用基于正交匹配追踪算法(OMP)实现数据规则化。与常规数据规则化方法相比，该方法规则化和插值更精确，解决了连片偏移处理中块与块之间覆盖次数不均造成的能量不均和偏移画弧问题。该技术在塔北隆起LG地震工区得到成功应用，新资料清楚地刻画出了奥陶系碳酸盐岩的潜山面，并能够更加准确地识别出奥陶系内幕孔洞型“串珠”储层特征。

关键词：数据规则化； 五维插值； OMP算法； 孔洞型储层； 碳酸盐岩

0引言

随着勘探开发的不断深入，对地震成像的精度要求也越来越高。精度更高的偏移算法要求原始资料的观测方式比较规则，覆盖次数较高，方位角以及偏移距分布比较均匀。然而在连片资料拼接处理时，在多块资料的交界区域，覆盖次数往往高达上百次，而正常覆盖只有几十次，有些区域因地表条件限制、面元不同或采集方位不同导致出现空洞。这些差异都会导致用于叠前偏移的地震数据空间采样不均匀[1-5]，偏移时容易产生假频，带来地震成像质量的下降(比如成像脚印问题、成像噪音问题及偏移画弧问题[3-4])。更重要的是，不规则的数据使得精度高的偏移方法的优势发挥不出来，导致成像振幅不保真，影响了成像的精度。因此，进行偏前数据规则化研究势在必行[5-6]。

实际生产主要应用的数据规则化方法有面元均化技术和加权补偿方法。面元均化技术是丢掉冗余道或者向相邻面元借道，在一定距离内补齐缺失道，其优点是可以消除高、低覆盖次数导致的能量差异，可以使得覆盖次数达到基本一致，面元内炮检距分布均匀；缺点是该方法修改了原始地震道的真实坐标，会导致叠前偏移出现空间假频，对叠前偏移效果带来很大的副作用。加权补偿方法主要采用基于覆盖次数的补偿方法，根据面元中覆盖次数，求取比例因子，然后对同一CMP道集应用相同的比例因子。优点是不会改变连片各工区原始覆盖次数和地震道坐标，能使叠前偏移的纯波数据体在能量上保持一致性。此方法较面元均化方法更易实现，缺点是该方法并不能弥补所有缺失的偏移距[7]。

这里针对目前数据规则化方法的特点，研究了基于OMP算法五维数据规则化技术，将空间上不规则的样点插值成规则均匀样点，在一定范围内补全缺失的地震道，从而消除地震资料空间采样不规则对成像效果造成的影响。同时内插后的地震数据具有完整的方位角、偏移距信息。该数据规则化处理前，要对地震资料进行预处理，如一致性拼接处理、近地表静校正、叠前去噪、地表一致性处理等，其中一致性拼接处理为数据规则化前比较关键的步骤。之后采用五维数据规则化技术，以得到高质量的道集，从而能够进行精确的速度拾取、准确的偏移成像。

1规则化前预处理

LG地区共有A、B、C、D四块地震工区，各次采集年代不同、观测系统也不同，但互有重叠，工区的炮点空间分布不规则(图1)。A、B、C三个工区的有效偏移距较小、覆盖次数低；D工区有效偏移距较大，覆盖次数高；A、B、D三个工区采集方位角基本一致；D工区纵横比最大；C工区采集方位与其他工区是垂直关系(图2)。不同区块本身覆盖次数不同，炮点分布不规则和不同区块重叠，导致覆盖次数空间变化大，不同面元内的道集偏移距分布也不规则。在偏移之前，必须做规则化处理。

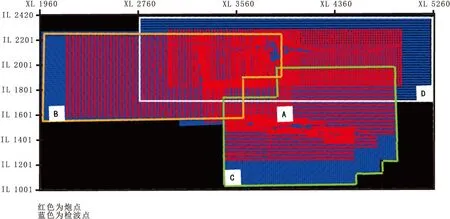
图1　LG地区三维地震炮、检点分布图Fig．1　Source and receiver points distribution of 3D seismic acquisition in LG district

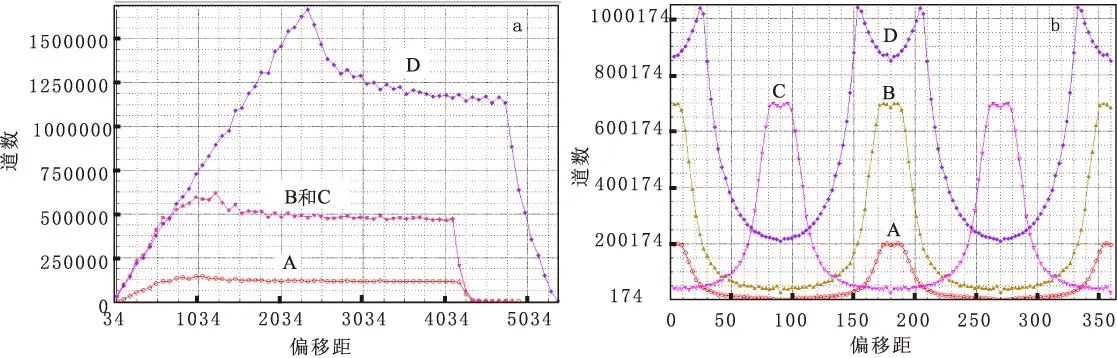
图2　LG地区三维地震分布图Fig．2　Offset distribution of 3D seismic data in LG district(a)偏移距分布图；(b)方位角分布图

不同年代采集的地震资料，采集参数不同，导致相位、时差、振幅能量及频率上都会有差异[5]。不一致的相位和时差会导致地表一致性静校正计算不准确以及动校正和偏移成像时不能同相叠加精确成像，不一致的振幅和子波会带来后续保幅和精准偏移成像困难，因此在进行数据规则化之前，须先解决不同工区地震子波的空间不一致性。

根据资料特点，设计针对性处理流程(图3)。通过相位一致性处理技术解决了相位和时差不一致问题(图4(a))；地表一致性反褶积解决了子波的一致性问题，横向分辨率趋于一致(图5)。采用地表一致性振幅补偿解决了相同地震工区内振幅能量差异，但叠加剖面上仍表现出振幅能量差异，其振幅能量差异来源于不同工区因覆盖次数不同导致。此外在野外采集施工时，由于地表变化、地表障碍等因素影响，造成炮、检点分布不规则，而在克希霍夫叠前偏移成像中不仅需要满足规则化网格点假设，而且需要满足覆盖次数保持一致，否则偏移成像中会出现较严重的偏移画弧现象，很难做到保幅成像。因此，解决能量不均和偏移画弧[7]等问题，需要进行数据规则化处理。

图3　地震数据预处理及五维数据规则化处理流程Fig．3　The flow of seismic routine processing and 5D regularization

2五维数据规则化基本原理

一般来说，数据规则化和插值的实现是，先将不规则网格点的数据从时间域进行傅里叶变换到空间

频率域，从而进行规则网格点的数据规则化和插值，再经过傅里叶反变换到时间域，进行数据规则化和插值时数据和维度选择[8]，即如何选择和排列数据，在什么样的维度上进行数据规则化和插值，同样是数据规则化和插值的关键。

正交匹配追踪(OMP)算法是基于傅立叶展开式表示输入数据以及用展开式的因子，在任何期望的空间位置来进行数据重建的。该方法在空间频率域中沿频率切片计算，并且能在2、3、4、5个空间维度中应用。偏移距的扩展(如坐标)是由不规则离散傅立叶变换计算出。在4维和5维插值中，共中心点或炮点坐标的扩展，使用分级的规则离散傅立叶变换计算出。为了清晰地了解其原理，这部分插值的扩展是用二维地震数据来说明。

假定f(xj)，(j=0…Nx-1)表示对于给定频率的空间频率域地震数据，其中Nx是地震道数，0≤xj≤xmax是每一道的空间坐标，则输入数据的扩展形式如下：

(1)

反变换如下：

(2)

公式(1)与公式(2)的右边能通过不规则快速傅立叶变换得到。

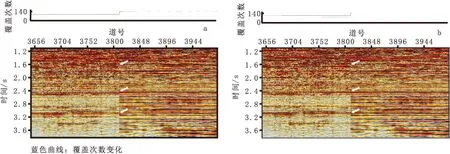
图4　相位一致性叠加对比图Fig．4　Seismic stack section phase consistency match(a)匹配前；(b)匹配后

图5　地表一致性叠加对比Fig．5　Seismic stack section surface consistent deconvolution(a)振幅补偿前；(b)振幅补偿后

空间波数kl与指数l有关，kl=2πl/xmax，(l=-Nk/2…Nk/2)，其中Nk表示空间频率的个数。假定最大波数为固定值，增加xmax的数值会导致波数域更加精细的采样率以及冗余扩展空间。同理，反过来会提高插值计算效率。通常xmax是数据中最大偏移距的4倍。

正交匹配追踪算法在公式(1)扩展时每次增加一个分量，经过m步后，误差表示为式(3)。

(3)

其中Pl是在第l步选取的系数的指数。算法的步骤描述如下：

初始化：设定m=0,R0(xj)=f(xj) 。

迭代过程：

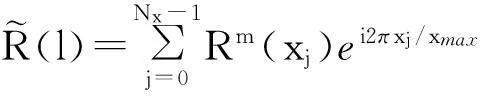
2)通过一个最小二乘最小化公式重新计算所有的系数。

3)通过公式(3)重新计算一个剩余值Rm+1(xj)。

4)当‖Rm+1‖变得足够小时或者当达到所允许系数的最大个数时终止。

这里步骤2)是通过共轭梯度方法计算，由于共轭梯度的解需要大量正向和反向的不规则傅立叶变换，这就导致增加计算量，但是减少了共轭梯度迭代次数(通常只需要5到10步)，因此，执行步骤2)是通过减少迭代次数减少了计算量。

选取数据规则化的维度也非常关键。常规的数据选择有共偏移距体(相同偏移距组的数据)、分方位角扇区共偏移距体(不同方位角相同偏移距的数据)、共偏移距矢量体(具有相近X和Y两个方向偏移距的数据)[6]，如图6所示。

用上述三种数据进行数据规则化，通常的做法是分别在不同部分的数据中分别进行纵向、横向和时间三个维度的数据规则化和插值，这忽略了数据在不同偏移距和不同方位角之间的联系，数据规则化和插值之后的数据不能很好地保真、保幅以及保持偏移距和方位角信息。将所有数据放在一起，在不同面元中同时考虑数据本身所包含的各种信息(纵向、横向、时间、偏移距、方位角)[8-10]，在不同区块、不同偏移距、不同方位角数据适当重叠以增加更多信息，进而进行数据规则化和插值必然更为精确，即五维数据规则化。

五维插值数据规则化是在频率域中运算，一旦建立了傅里叶系数，即可运用相应的算法重建规则数据输出。获得不规则采样数据的傅里叶系数并不是很直接，需要解决的一个问题是从振幅强的傅里叶系数向振幅弱的傅里叶系数渐变的过程中会有漏失。另外，为了获得有意义的系数，输入的主测线和联络测线必须有典型的偏移距，这是需要采用“超道集”的原因。“超道集”需要足够大，以包含所需的偏移距能够重建，但是也不能太大而包含太多的远数据点。

基于OMP算法五维数据规则化技术与常规技术的区别是：①是综合考虑了“纵向、横向、时间、偏移距、方位角”五个维度；②是定义输出观测系统，重新构建道集；③是实现了不同面元内炮检距和方位角规则分布。而常规技术仅仅考虑“纵向、横向、时间”三个维度，能够弥补部分缺失的炮检距，但不能实现炮检距均匀分布，容易导致叠前偏移出现空间假频。

3实例效果分析

图6　数据规则化和插值时不同数据的选择和排列示意图Fig．6　The choice and interpolation arrange of the different seismic data in data regularization and interpolation (a)共偏移距体；(b)分方位角扇区共偏移距体；(c)共偏移距

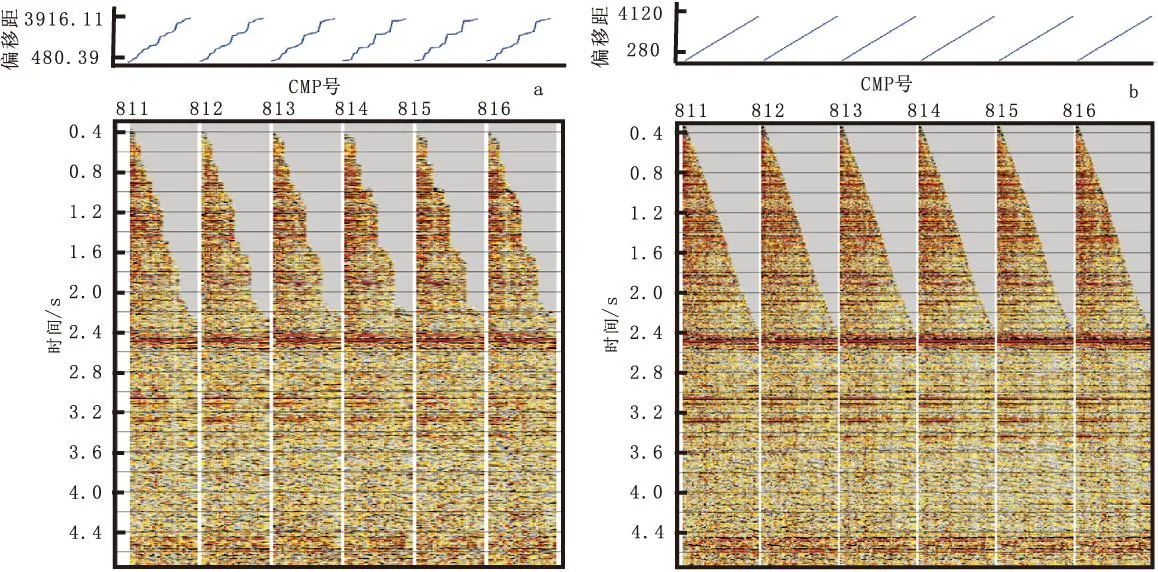
图7　五维数据CMP道集对比Fig．7　The contrast of CMP gathers before and after 5D regularization(a)规则化前；(b)规则化后

为了验证该技术在数据规则化方面的有效性，对塔里木盆地塔北隆起LG地区地震资料进行了方法验证和效果测试。测试取得了较好的实际应用效果。五维数据规则化前、后的CMP道集，五维插值数据规则化技术之后，道集偏移距分布更规则、信噪比更高(图7)。采取五维插值数据规则化技术，不仅实现了整个工区具有比较一致的覆盖次数，解决了区块间能量不一致问题，避免了叠前偏移的画弧现象，而且目的层潜山面较原偏移成像改善明显，能量更均衡、连续性变好(图8)，能够准确识别内幕溶洞“串珠”[11]。

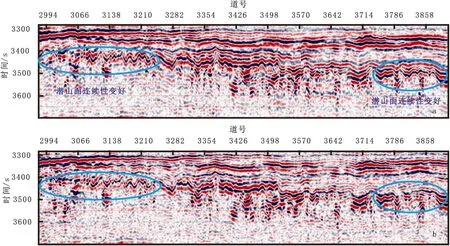
图8　五维插值数据规则化技术对比Fig．8　The contrast of the seismic migration section(a)偏移剖面；(b)老剖面

4结论与认识

陆上地震资料，由于受野外采集环境的限制、人为施工的误差，不同年度采集地震资料的拼接都可能导致用于叠前偏移的地震数据空间采样不均匀。作者正是基于这方面的考虑，提出了基于叠前五维数据规则化的一种新思路，充分利用地震数据的五个维度，来构建规则道集，实际资料的应用效果证明了该技术的实用性。

基于正交匹配追踪算法的五维数据规则化技术，能够有效消除偏移距、覆盖次数、方位角等分布不规则对能量和成像效果的影响，对改善面元属性、炮检距分组、提高数据信噪比及偏移成像质量优势明显，能够解决不同区块和拼接区之间偏前覆盖次数不均，偏移剖面上振幅能量不均和成像失真等问题；同时该方法为陆上采集炮、检点灵活布置提供了条件。

该技术同样适用于3维或4维数据规则化插值，即可以去掉偏移距和方位角信息。但是更多空间维度的插值算法有很多的优点，特别是同时在5个地震数据维度进行插值，能够很好地通过修正振幅和相位变量来预测缺失的地震数据。

参考文献：

[1]张红梅，刘洪. 基于稀疏离散τ-p变换的叠后地震道外推 [J]. 物探化探计算技术，2007，29(1)：1-6.

ZHANG H M，LIU H. Sparseness discrete τ-p transform in poststack seismic trace extrapolaion[J].Computing techniques for geophysical and geochemical exploration，2007，29(1)：1-6.(In Chinese )

[2]徐辉，张军华. 面元细分处理资料的分辨率定量评价[J]. 物探化探计算技术，2010，32(1)：59-63.

XUE H，ZHANG J H.The quantitative evaluation of resolution for seimic data processing by bin-dividing[J].Computing techniques for geophysical and geochemical exploration，2010，32(1)：59-63.(In Chinese)

[3]石颖，张振，王建民，等. 地震数据反假频规则化方法研究[J]. 地球物理学进展，2013，28(1)：0250-0256.

SHI Y，ZHANG Z，WAGN J M，et al. Investigation on de-alias regularization approach for seismic data[J]. Progress in Geophys，2013，28(1):0250-0256.(In Chinese )

[4]刘礼农，周立宏，朱振宇，等. 复杂观测系统下的三维波动方程叠前深度偏移[J]. 地球物理学进展，2002，17(4)：658-662.

LIU L N，ZHOU L H，ZHU Z Y，et al.3D wave equation prestack depth migration with complex Layouts [J]. Progress in Geophys，2002，17(4)：658-662.(In Chinese )

[5]高建军，陈小宏，王芳芳，等.不规则地震道数据规则化重建方法研究[J]. 地球物理学进展，2011，26(3)：983-991.

GAO J J，CHEN X H，WANG F F，et al. Study on regularized reconstruction of uneven seismic traces. [J]. Progress in Geophys，2011，26(3)：983-991.(In Chinese )

[6]王棣，马秀红，崔兴福，等. 偏移距规则化技术在叠前时间偏移中的应用[J]. 勘探地球物理进展，2009，32(1)：44-47.

WANG D，MA X H，CUI X F，et al. Application of prestack offset regularization prestack time migration[J]. Progress in Exploration Geophysics ，2009，32 ( 1)： 44- 47. (In Chinese)

[7]赵忠华，初海红，陈志德. 频率-空间域叠前数据规则化技术研究及其应用[J]. 油气藏评价与开发，2013，3(2)：15-20.

ZHAO Z H，CHU H H，CHEN Z D. Research on frequency-spatial domain prestack data regularization and its application[J].Reservoir Evaluation and Development，2013，3(2)：15-20.(In Chinese)

[8]KAWIN NIMSAILA， PING WANG.Fast progressive sparse Tau-P transform for regularization of spatially aliased seismic data[C]. The 76thEAGE conference and exhibition，2014：230-234.

[9]G.POOLE， P.HERMANN.Multi-dimensional data regularization for modern acquisition geometries[C]. The 69thEAGE conference and exhibition incorporating SPE EUROPEC， 2007：70-75.

[10]SHENG XU， YU ZHANG， GILLES LAMBARE.Anti-leakage Fourier transform for seismic data regularization practice in higher dimensions[J]. Geophysics， 2010，70(4)：87-95.

[11]高彩霞.波动方程叠前成像数据规则化技术研究与应用[J]. 石油天然气学报，2010，32(6)：271-273.

GAO C X. Technical Study and Application of Wave Equation Prestack Imaging Data Rule[J]. Journal of Oil and Gas Technology，2010，32(6)：271-273.(In Chinese)

5D regularization processing based on OMP arithmetic in seismic data CUI Yong-fu1,2， MIAO Qing2， DANG Qing-ning2

WU Guo-chen1， PEI Guang-ping2， YUAN Yuan2

(1. School of Geosciences，China University of Petroleum(Huadong), Qingdao286580， China；2. Research Institute of Exploration and Development，Tarim Oilfield Company， PetroChina， Korla841000， China)

Abstract:Regularization of seismic data is one of the important technologies in seismic data processing. It can improve bin properties, seismic S/N ratio and seismic migration imaging. It is different from the conventional data regularization methods, 5D regularization based on OPM arithmetic comprehensively utilizes 3D seismic data in five dimensions including longitudinal coordinate, transverse coordinate, time, offset, and azimuth angle, leading to the regularization and interpolation more precise. This method is successfully applied in LunGu 7 district of Tabei lift in Tarim basin. The results show that this technology solves the problem of uneven amplitude and migrating arcing caused by fold uneven between contiguous blocks in PSTM processing. The new seismic data can describe clearly the surface of burial hill of Ordovician dolomite and the "string" characteristics in interior burial hill.

Key words:regularization； 5D interpolation； orthogonal matching pursuit； cavity reservoirs； carbonate

中图分类号：P 631.4

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.01.10

文章编号：1001-1749(2016)01-0067-07

作者简介：崔永福(1978-)，男，博士，高级工程师，主要从事石油物探工作， E-mail：cuiyongfu-tlm@petrochina.com.cn。

基金项目：国家重点基础研究发展计划(2013CB228604)； 国家油气重大专项(2011ZX05046, 2011ZX05019-003, 2011ZX05009-003-004)

收稿日期：2014-19-09改回日期：2015-05-15