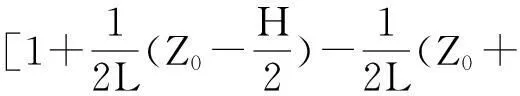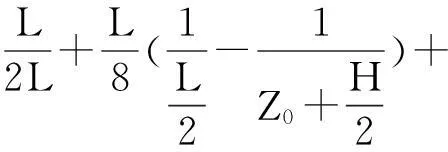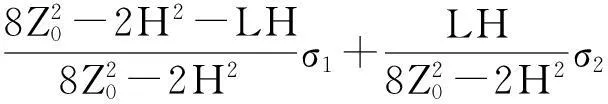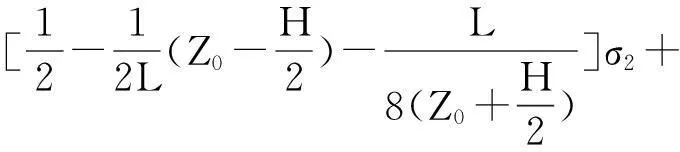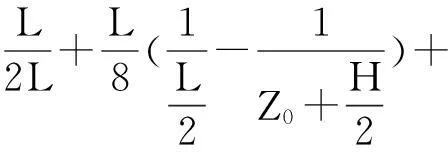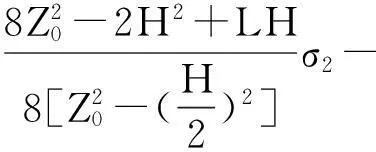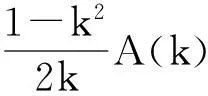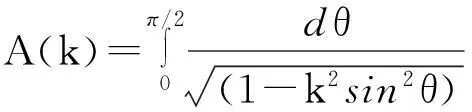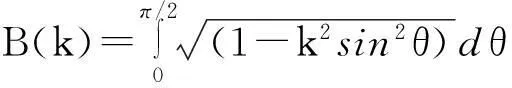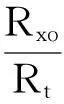感应测井几何因子理论计算及其应用

彭　玲， 潘和平

(中国地质大学　地球物理与空间信息学院,武汉　430074)



感应测井几何因子理论计算及其应用

彭玲， 潘和平*

(中国地质大学地球物理与空间信息学院,武汉430074)

摘要：几何因子对于计算地层真实电阻率、了解地层特性、划分储层等起着相当重要的作用。这里建立双线圈系感应测井基本模型，分别得出纵、径向简单多层地层模型的几何因子理论曲线，从中可得知感应测井响应值受到目的层厚度、围岩电阻率、泥浆电阻率、侵入带等多种情况的因素影响，①目的层越厚，感应测井值越接近原状地层电阻率值；②在过渡带厚度不变的情况下，冲洗带深度越大，测量的电阻率越小，它的径向几何因子有下降的趋势，但是整体来说，随着冲洗带的半径增加，视电导率增加幅度变缓，且越来越接近过渡带地层的电导率；③在冲洗带厚度不变的情况下，过渡带的深度越小，越接近原始地层的电导率；④泥浆侵入会导致得到的地层电阻率与实际地层电阻率存在较大偏差。将这些结论应用于计算塔河油田石炭系区域井的真实电阻率中，得到塔河油田石炭系区域地层电阻率真值，最后解释结果与试油结果对比证实,这一过程确实提高了地层电阻率和冲洗带电阻率的精度。

关键词：双感应测井； 几何因子； 塔河油田石炭系区域

0引言

几何因子可以很好地解释周围地层对测量信号的贡献，从而可以计算得到地层的真实电阻率，所以研究几何因子对于了解地层特性、划分储层等起着相当重要的作用。Doll[1]几何因子是Doll在1949年提出感应测井方法的同时就给出了的,它是从电磁场方程在忽略趋肤效应的影响的条件下导出的，因存在一定不足，此后有学者相继提出新的几何因子， Gianzero 等人[2]提出了考虑趋肤效应的几何因子-Gianzero几何因子； Moran[3]推导出的Moran几何因子，指出其具有对称性和实际物理意义；Howard 等人[4]将量子散射问题中的 Born 近似方法应用于非均匀地层中的感应测井问题，导出感应测井中的Born 近似公式。这里就Doll几何因子进行理论计算，并将结论应用于计算塔河地区的真实电阻率值上。从空间上来划分，Doll几何因子可以分为径向几何因子与纵向几何因子。在解释中，它可以描述仪器的径、纵向特征，分析不同地层部分对所测量信号的影响[5]。

1双线圈系纵向几何因子模型计算

1.1简单三层地层模型

以双线圈系感应测井仪为例，釆用简单的三层模型进行讨论，计算不同情况下的几何因子。已知全空间的几何因子为“1”，对于一般常用的感应测井而言，井眼的影响可以忽略不计，故当观测点为接收线圈中点时，围岩电导率与地层电导率之和为“1”。如图1所示，H为目的层厚度；d为井眼直径；σ1为围岩电导率；σ2为目的层电导率,σ1>σ2。G1为围岩几何因子,G2为目的层几何因子。模型的视电导率σa可以表示为式(1)。

σa=σ1G1+σ2G2=σ1(1-G2)+σ2G2

(1)

图1　简单三层介质示意图Fig．1　Sketch map of a simple three layer medium

研究分析双线圈探头与边界相对位置的几种情况：

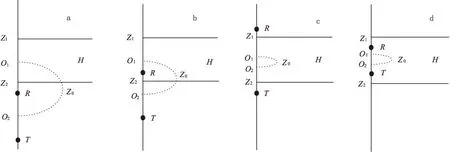
在图2中，T、R分别为双感应测井仪接收线圈，接收线圈距L=1 m，O2为接收线圈中点，O1为地层的中点，假定O2始终为坐标系原点，Z1、Z2为地层的上、下坐标，Z0为接收线圈中点与岩层中点的距离,H为地层厚度。令σ1为围岩电导率，σ2为目的层电导率,σ1>σ2，σa为视电导率。

1)探头位于地层外部(图2(a))， 根据纵向积分几何因子公式可得地层外部的几何因子Go，gz为Doll几何因子：

(2)

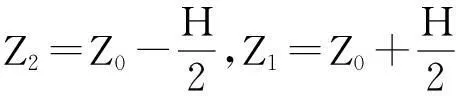
(3)

σa=σ1(1-G)+σ2G

(4)

2)一个探头位于地层外部，另一个探头位于地层内部。对于探头位于如图2(b)所示，将探头内、外的地层几何因子相加可得出层厚为H的地层的几何因子。设地层内部几何因子为Gi,外部几何因子为Go。

(5)

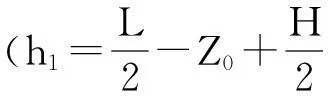
(6)

则该层的几何因子为：

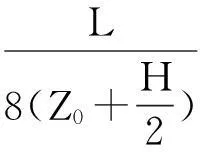
(7)

当接收线圈中点位于地层分界面上时，h1=L/2,Z0=H/2,带入式(7)，得到界面几何因子Gs：

(8)

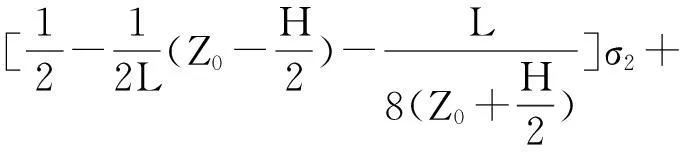
(9)

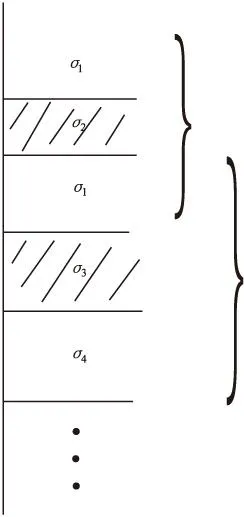
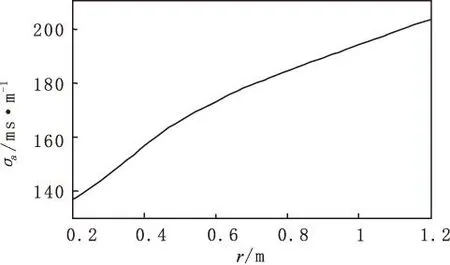
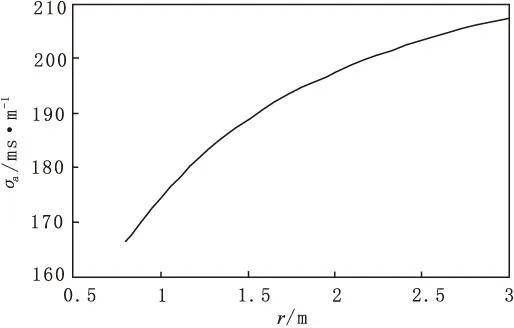
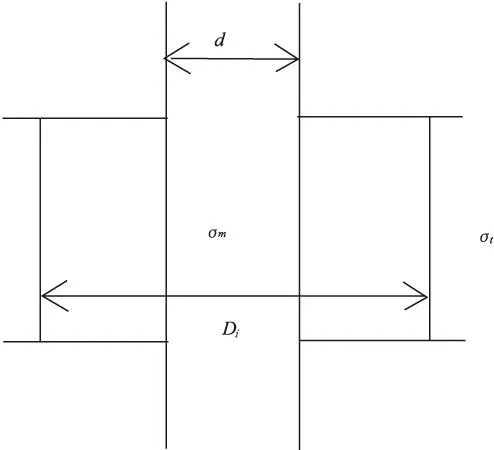
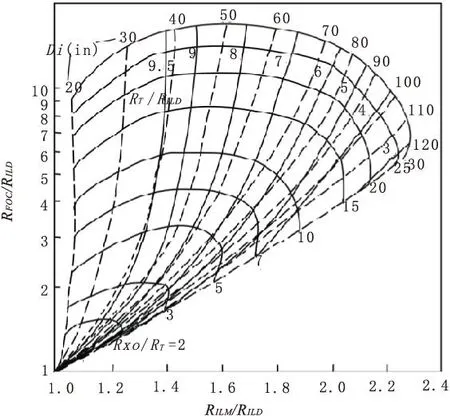
3)探头位于地层内部。

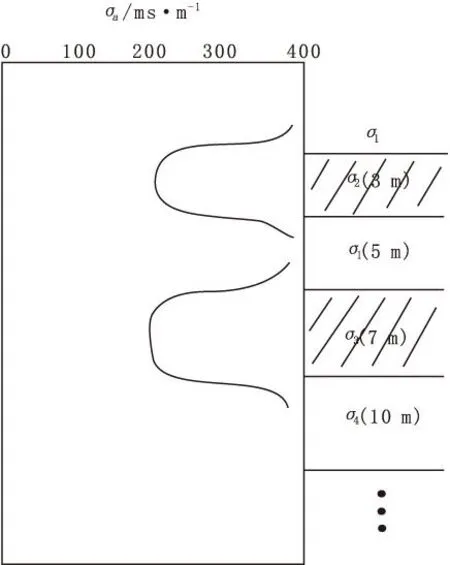
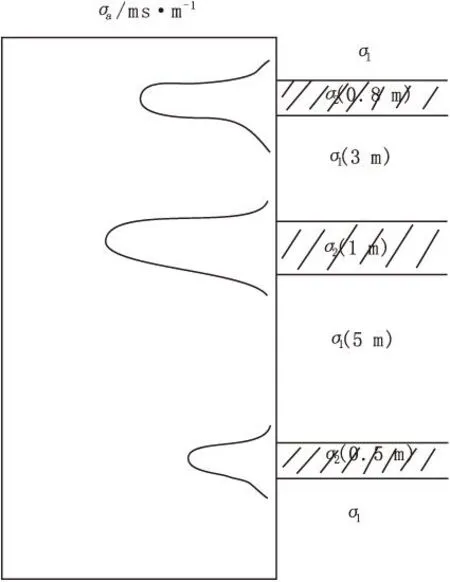
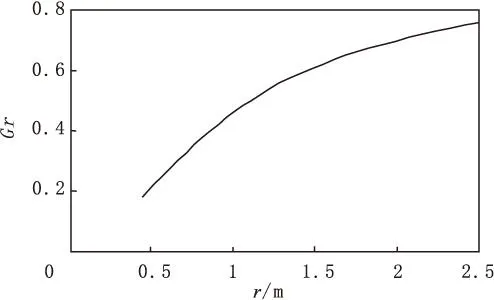
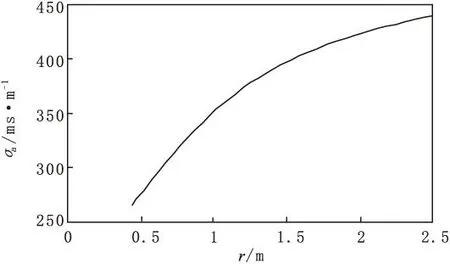
当H

如图2(c)所示，地层的几何因子为：

(10)

(11)

当H>L时：

对于探头位于如图2(d)所示位置，将探头内、外的几何因子相加可得到层厚为H的地层的几何因子。

图2　探头与层界面相对位置示意图Fig．2　Probe and interface relative location diagram

(12)

(13)

当记录点位于地层的中点时，则Z0=0,假设模型中的L=1，视电导率为：

(14)

当地层厚度很厚时:

G≈1, σa=σ2

当记录点位于地层的边界上时，则Z0=H/2,假设模型中的L=1，视电导率为：

(15)

当地层厚度很大时:

(16)

当记录点位于地层以上或者以下很远时，即H很大，Z0很大，假设模型中的L=1，视电导率为：

G≈0,σa=σ1

(17)

从式(17)可看出，当地层厚度很大时，可以用半幅值点分层。

1.2简单多层厚层模型(H>L)

研究讨论多层的情况下几何因子的大小情况，σ1-σ4分别是不同地层的电导率，如图3所示，先研究上三层，可将σ1看成围岩，σ2为目的地层，再研究下三层，为了能连续成图，研究几何因子的规律，故将σ1、σ4假设成围岩，σ3假设成目的地层，目的层厚度为H，Z0为接收线圈中点与岩层中点的距离。进行下三层计算。假设接收线圈从上向下移动，每一个层厚都比接收线圈距大，接收线圈中点为坐标原点，则几何因子为：

1)线圈全在电导率为σ1的地层。

(18)

σa=σ1(1-G)+σ2G=

(19)

图3　简单多层厚层　　地层模型Fig．3　A simple multi-layer 　　　thick layer model

2)线圈一半在电导率为σ1的地层，一半在目的地层。

(20)

(21)

3)线圈全在电导率为σ3的地层。

(22)

(23)

假设层厚远远大于接收线圈距时，图3中自上而下，令σ2层厚度为3 m,σ1层厚为5 m,σ3层厚度为7 m,σ4层厚度为10 m，L=1 m画出多层厚层感应测井曲线如图4所示。

图4　多厚层感应测井曲线Fig．4　Thick layer of induction 　　　logging curves

可以看出，即使H很厚，计算的视电导率的值也是高于真实电导率值的，研究表明，相对于目的层电导率，围岩电导率越大这种差异越大，只有在目的层厚度非常厚的时候，双线圈系感应测井响应值才能接近真实地层电导率,而且厚层地层一般可以用半幅值点分层，且效果较好。

1.3简单多层薄层模型(H

对于厚层而言，当假设H很大时，近似计算得到厚层能用半幅值点分层的结论，在薄层不适用，很明显，薄层一般不能使用半幅值点分层。电导率为σ2的地层为目的地层，σ1看成围岩。

在图5中，电导率为σ2的地层开始，自上而下的厚度分别为0.8 m、 3 m、1 m、5 m、0.5 m、L=2 m根据计算的内容画出多层薄层感应测井曲线。

图5　简单多薄层地层模型 Fig．5　Simple multi-layer 　　　formation model

图6　多薄层感应测井曲线Fig．6　Multi-layer induction 　　logging curves

分析结果可以得出，对于薄层而言，一般测得的视电导率是大于真实地层的视电导率的，且不能用半幅值点分层，实际处理中，一般将曲线的2/3幅值点用于分层。

2双线圈系径向几何因子模型计算

2.1含侵入带的三层地层模型

研究分析含侵入带模型(图7)，主要考察侵入带的深度变化对几何因子大小的影响，以及视电导率的影响。

图7　含侵入带的三层模型Fig．7　Three layer model with the 　　　invaded zone

假设侵入带与原状地层的接触面为“平滑圆柱面”，L=1 m,井径直径d=0.25 m,泥浆电导率σm=1 000 ms/m、冲洗带电导率σs=500 ms/m、围岩电导率σi=250 ms/m、过渡带电导率σt=200 ms/m，侵入带的半径为r，令r分别为0.45 m、0.5 m、1 m、1.5 m、2 m、2.5 m。井径的几何因子为：

=0.0164

(24)

其中：

(25)

侵入带几何因子Gq=Gr-Gd/2,因几何因子在整个空间为“1”，则地层的几何因子为：

Gt=1-Gq-Gd/2

(26)

地层的视电导率为：

σa=σmGm+σsGs+σtGt

(27)

由图8、图9可以看出，理论计算曲线与模型理论计算曲线的形态基本一致，这就说明了模型建立与计算的正确性。由图10可以看出，随着深度的增加，侵入带几何因子数值增加，地层几何因子数值减少，说明地层真实电阻率对测量的结果的贡献越来越小，侵入深度对测量结果的影响还是非常大的，这也是双线圈系的一个不足之处。

图8　径向积分几何因子曲线Fig．8　The radial integral geometry 　　　factor curve

图9　模型计算侵入带几何因子曲线Fig．9　Invaded zone geometry factor 　　　curve calculation model

图10　模型计算视电导率曲线Fig．10　Model for calculating the apparent 　　　conductivity curve

2.2含冲洗带与过渡带的三层地层模型

这里将分别分析冲洗带与过渡带的深度对径向几何因子的影响。

图11　含冲洗带和过渡带的三层地层模型Fig．11　Including irrigation zone and 　　　transition zone of the three 　　　layer model

如图11所示，d为井径，ri为冲洗带半径，rs为过渡带半径，σm为泥浆电导率，σi为冲洗带电导率，σs为过渡带电导率，σt为原状地层电导率，σw为围岩电导率。

1)冲洗带深度影响。

在对比冲洗带深度影响时，我们考察rs-ri值不变,即过渡带厚度不变.令σm=1 000 ms/m,σi=250 ms/m，σs=200 ms/m，σt=100 ms/m，σw=50 ms/m。d=0.2 m，H=5 m，ri分别为0.2、0.3、0.5、0.8、1.2；rs相对应的值分别为0.5、0.6、0.8、1.1、1.5。

(28)

其中：

视电导率为：

σa=σmGm+σiGi+σsGs+σtGt

(29)

计算径向几何因子，得到图12、图13。

图12　冲洗带径向几何因子Fig．12　Flush with radial geometric factor

图14　视电导率随着冲洗带半径变化曲线Fig．14　The apparent conductivity 　　　with flushed zone radius curve

由图12可以看出，随着冲洗带深度的增大，冲洗带的径向几何因子增加；过渡带的厚度虽然不变，但是随着整体向原装地层的深入，它的径向几何因子有下降的趋势。但就整体来说，冲洗带的半径增加,视电导率增加幅度不大 ，且越来越接近过渡带地层的电导率。

2)过渡带深度影响。

考虑过渡带深度的影响，即考虑冲洗带厚度不变(ri不变)，令σm=1 000 ms/m，σi=250 ms/m，σs=200 ms/m，σt=100 ms/m，σw=50 ms/m。d=0.2 m，H=5 m，ri=0.6；rs分别为0.8、1.2、1.8、2.6、3.6。

图15　过渡带径向几何因子Fig．15　The transition with radial 　　　geometric factor

图16　过渡带视电导率曲线Fig．16　Transition band of apparent 　　　conductivity curve

由图16中可以看出，过渡带的深度越小，越接近原始地层的电导率。

3感应测井真电阻率计算

塔河油田石炭系油藏分布在卡拉沙依组，为砂泥岩互层剖面。由于钻井液滤液的电阻率大于地层水的电阻率，所以在石炭系的钻井液侵入一般为高侵，RFOC>RILM>RILD或RFOC>RILM≈RILD[7]。因此，对于水层而言，由于高阻侵入的影响，实测的RILD会增高；对于油气层而言，由于高阻侵入的影响，实测的RFOC会减小，如果利用RFOC计算地层冲洗带含水饱和度将会偏高，导致解释过高的可动油气量[8]，所以要做钻井液侵入校正[9]。

为了研究泥浆侵入带的影响，设地层为无限厚层(即不考虑围岩的影响)，泥浆侵入[10]呈台阶型即侵入带与原状地层间的界面为圆柱面、电阻率是突然变化的(图17)。在这种具有泥浆侵入带的三层介质条件下，对一般井眼与含盐量不高(非盐水)泥浆以及常用的感应测井仪来说，井眼的影响可以忽略不计。在这种情况下，感应测井视电导率σa主要决定于侵入带电导率σi侵入带直径Di及原状地层的真电导率σt，按几何因子理论,可表示为：

σa=σiGi+σtGt=σiGi+σt(1-Gi)

(30)

式中：Gi为侵入带的积分几何因子；Gt为原状地层的积分几何因子。

式(30)包含σi、σt和Di三个未知数，需用三个方程求解，因此，这里采用双感应-浅聚焦测井综合图版法，求解地层电阻率Rt、冲洗带电阻率Rxo和侵入带直径Di[11]。

图17　泥浆侵入带三层模型 Fig．17　Mud invasion zone 　　　three layer model

图18为解释图版，纵坐标为浅聚焦测井电阻率RFOC与深感应测井电阻率RILD的比值，即RFOC/RILD。横坐标为中感应测井电阻率RILM与深感应测井电阻率RILD的比值，即RILM/RILD。图18中有三组曲线，横实线的号码为Rxo/Rt，纵虚线的号码为Di，纵实线的号码为Rt/RILD，这是适合于泥浆高侵的解释图版。

图18　双感应-浅聚焦测井综合图版Fig．18　Dual induction - shallow focus 　　　logging comprehensive chart

由几何因子理论知[12]：

(31)

(32)

RFOC=JRxo+(1-Js)Rt

(33)

式中：GD为深感应侵入带的积分几何因子；GM为中感应侵入带的积分几何因子；JS为浅聚焦在侵入带的近似几何因子。根据式(31)-式(33)可得：

(34)

(35)

(36)

当给定Rxo/Rt和Di时，由双感应-浅聚焦测井综合图版读数可计算出唯一的GD、GM和Js，然后可用式(37)与式(38)计算得到Rt和Rxo。

(37)

(38)

经过上述计算后，我们得到经过侵入校正后的视电阻率值。式(39)中σa为上述计算中经过侵入校正后得到的视电导率，σ1为仪器测得的视电导率，σ2则为最后需得到的真电导率的值。

σa=σ1G1+σ2G2=σ1(1-G2)+σ2G2

(39)

可以分别计算出储层几何因子G2，已知σa、σ1，即可求出真电导率σ2，进而通过上式算出地层的真电阻率Rt。

4成果分析

图19中RILD、Rt分别为校正前、后的地层电阻率(深感应测井值)；RFOC、Rxo分别为校正前、后的冲洗带电阻率。根据含水饱和度公式与阿尔奇公式[13]可以推导出：

(40)

我们分析研究图19中通过常规测井与已知资料划分的5个储层：①5 033 m～5 039.5 m校正前、后Rt变化不大，Rxo降低1 Ω·m～3 Ω·m，Rxo/Rt较校正前增加2.3，显示为水层特征；②5 110 m～5 113.5 m,Rxo/Rt=3,较校正前只增加0.07，显示为油水同层特征；③5 164 m～5 168 m段Rxo/Rt=6.5，显示为水层特征；④5 179 m～5 182.5 m段校正后，比值减小0.41，显示为油层特征；⑤5 215 m～5 222 m，Rxo/Rt=6.6，显示为水层特征。

根据曲线形态，并结合已知油气层测试资料，图19中5层分别为水层、油水同层、油水同层、油气层、油气层。解释结果大致与实际相同，说明此方法是正确而适用的。

解释结果中，1～5分别为水层、油水同层、油水同层、油气层、油气层。校正后的电阻率值Rt更接近试油电阻率，侵人降低了利用测井资料区分水层与油气层的分辨率，而此方法提高了冲洗带电阻率和地层电阻率的精度。

5结论

通过计算不同模型下的Doll几何因子，分别得出层厚、侵入带等对几何因子的影响规律，并将其应用到新疆塔河油田石炭系地层中，计算其实际电导率值的大小，取得了较好的解释结果，得到如下结论：

1)目的层越厚，感应测井值越接近原状地层电阻率值，而且厚层地层一般可以用半幅值点分层，且效果较好；对于薄层而言，一般测得的视电导率是大于真实地层的视电导率的，且不能用半幅值点分层，在实际资料处理中，一般将曲线的2/3幅值点用于分层。

2)在过渡带厚度不变的情况下，冲洗带深度越大，测量的电阻率越小，它的径向几何因子有下降的趋势，但就整体来说，随着冲洗带的半径增加，视电导率增加幅度变缓，且越来越接近过渡带地层的电导率；冲洗带厚度不变的情况下，过渡带的深度越小，越接近原始地层的电导率。

3)感应测井响应值受到目的层厚度，围岩电阻率，泥浆电阻率，侵入带等多种情况的因素影响。

4)泥浆侵入会导致得到的地层电阻率与实际地层电阻率存在较大偏差，试油结果与解释结果对比，说明校正后的电阻率值更加接近真实电阻率，侵入校正提高了地层电阻率的精度。

图19　S46深感应与浅聚焦侵入校正前后结果对比Fig．19　Contrast S46 before and after correction results of deep and shallow inductio

图20　S46真电阻率成果图Fig．20　S46 true resistivity figures

参考文献：

[1]DOLL H G. Introduction to induction logging and application to logging of wells drilled with oil base mud [J]. Journal of Petroleum Technology,1949, 186: 148-162.

[2]GIANZERO S, ANDERSON B. A new look at skin effect[J]. SPWLA 22nd Annual Logging Symposium, 1981,23(1):20-34.

[3]MORAN J H. Induction logging- geometrical factors with skin effect[J].The Log Analyst，1982，23(6):4-10.

[4]HOWARD A Q, CHEW W C. A new correction to the born approximation[J].IEEE Transaction on Geoscience and Remote Sensing, 1990,28(3):394-399.

[5]王文新，杨志强，吴健，等.感应测井几何因子的对比研究[J].电波科学学报,2011(10)：348-351.

WANG W X, YANG Z Q, WU J, et al. Comparative study of induction logging geometrical factor[J]. Chinese Journal of Radio Science,2011(10):348-351.(In Chinese)

[6]张庚骥．感应测井的各次几何因子[J]．华东石油学院报，1979(2):1-6.

ZHANG G J. The geometric factors of induction logging[J]. East China Petroleum Institute Report,1979(2):1-6. (In Chinese)

[7]田中元,闰伟林,秦开明.淡水钻井液侵人条件下储层电阻率的变化研究[J].测井技术,2003, 27(2):113-227.

TIAN Z Y, RUN W L, QIN K M. Study on the changes of reservoir resistivity under the condition that the invasion of fresh drilling mud[J]. Well logging technology,2003,27(2):113-227. (In Chinese)

[8]秦绪英,陈有明,陆黄生.应用可动水分析方法确定储集层性质[J].石油物探，1996(1):54-58.

QIN X Y, CHEN Y M，LU H S. Using water analysis method to determine the nature of the layer reservoir[J]. Geophysical prospecting for petroleum, 1996(1):54-58.(In Chinese)

[9]潘和平,樊政军,马勇.电阻率测井的钻井液侵入校正方法[J].天然气工业，2005,25(7):41-43.

PAN H P, FAN Z J, MA Y. Correction method of drilling fluid invasion of resistivity logging[J]. Natural gas industry,2005,25(7)：41-43. (In Chinese)

[10]雍世和.测井数据处理与综合解释[M].北京：石油工业出版社，1982.

YONG S H. Logging data processing and comprehensive interpretation[M]. Beijing:Petroleum Industry Press,1982. (In Chinese)

[11]范翔宇,夏宏泉,陈平，等.测井计算钻井液侵入深度的新方法研究[J].天然气工业,2004,24(5): 65-70.

FAN X Y, XIA H Q, CHEN P. Research on a new method of calculating the depth of invasion of drilling fluid logging[J]. Natural gas industry,2004,24(5):65-70.(In Chinese)

[12]宋子齐,谭成仟,夏克文,等.视电阻率测井资料环境影响校正[J].测井技术,1995,9(4):250-261.

SONG Z Q, TAN C Q, XIA K W. Apparent resistivity logging data correction for environmental effects[J]. Well logging technology,1995,9(4):250-261. (In Chinese)

[13]潘和平,马火林,蔡柏林,等.地球物理测井与井中物探[M].北京：科学出版社，2009.

PAN H P, MA H L, CAI B L,et al. Geophysical well logging and borehole geophysical prospecting[M]. Beijing: Science Press,2009. (In Chinese)

Theoretical calculation and application of geometric factor of induction log

PENG Ling, PAN He-ping*

(Institute of Geophysics & Geomatics, China University of Geosciences, Wuhan430074, China)

Abstract:Geometric factor plays an important role in the respects of calculating the true resistivity of the formation, characterizing the formation properties, and distinguishing the reservoir. We established a basic model of the double coil induction logging, and derived the theoretical curves of the geometric factors of both the longitudinal and radial multi-layer formation models. The conclusion could be drawn from the curves, that the response values of the induction logging are influenced by the thickness of the target layer, the resistivity of the surrounding rocks, the resistivity of the mud filtrate, and the resistivity of the flushed zone. The response values of the induction logging will be closer to the resistivity values of the undisturbed zone when the thickness target layer is larger. When the thickness of the transitional zone is constant, the measuring resistivity will become smaller as the thickness of the flushed zone increases, and the radial geometric factor will decrease at the same time. In general, when the radius of the flushed zone increases, the increasing tendency of the apparent resistivity becomes slower, and the value of the apparent resistivity gets closer to the resistivity of the transitional zone. When the thickness of the flushed zone is constant, the response values of induction logging will be closer to the resistivity of the undisturbed zone as the thickness of the transitional zone decreases. In addition, mud invasion will cause relative big deviation between the measured formation resistivity and the real formation factor. We applied these conclusions in calculating the true resistivity of the boreholes in the carboniferous formation of Tahe oilfield, China. The calculated true resistivity of the formation was compared with the well testing results, and the accuracy of calculation of formation resistivity as well as the flushed zone resistivity was improved from this process.

Key words:dual induction logging; geometric factor; Tahe oilfield carboniferous area

中图分类号：P 631.8

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.01.02

文章编号：1001-1749(2016)01-0008-11

作者简介：彭玲(1992-)，女,博士，从事地球物理测井方向研究，E-mail:polly199209@hotmail.com。*通信作者：潘和平(1955-)，男,博士，教授,长期从事地球物理测井方面的教学和科研工作，E-mail:panpinge@publie.wh.hb.en。

收稿日期：2014-12-16改回日期：2015-05-09