地震信号时频分析中的希尔伯特黄变换研究

周竹生， 罗勇涛

(中南大学　地球科学与信息物理学院，长沙 410083)



地震信号时频分析中的希尔伯特黄变换研究

周竹生， 罗勇涛*

(中南大学地球科学与信息物理学院，长沙 410083)

摘要：随着时频分析方法的发展，生产研究上对复杂信号的时频分析有了更高的要求。这里简要介绍了希尔伯特—黄变换的原理和实现步骤，然后对合成信号进行经验模态分解(EMD)和希尔伯特谱分析，进而将HHT方法运用到实际地震信号的时频分析中。在此基础上，运用经验模态分解对合成地震信号进行了阀值去噪，证明了该去噪方法的有效性。

关键词：希尔伯特—黄变换； 经验模态分解； 地震信号； 时频分析； 时频滤波

0引言

在地震勘探中，由于地下介质的复杂性以及采集过程中的各种因素的干扰，获得的地震信号具有非线性、非平稳等特征，是一种典型的非平稳随机信号[1-2]。在以往的地震资料分析处理等研究中，傅立叶变换和功率谱估计都是基于平稳信号分析处理理论建立起来的，只能得到整个信号的频率成分，不能同时得到信号的时间和频率分辨率。短时傅立叶变换、小波变换和Cohen类等时频分析方法，虽然可以得到信号在不同时间、不同频率处的能量密度和强度，但由于这类方法还是基于傅立叶分析理论，因而也受到傅立叶分析不足的制约。1998年Norden. E. Huang等[3]发表了希尔伯特黄变换(Hilbert-Huang Transform，HHT)的相关论文。该方法主要分两步：①自适应的经验模态分解(Empirical Mode Decomposition，EMD)，得到有限个固有模态函数(Intrinsic Mode Function，IMF)；②进行希尔伯特变换，得到信号的瞬时频率和振幅，进而得到希尔伯特谱。

地震信号作为一种复杂的非线性信号，其时频分析方法自然也可以采用HHT方法，这里将HHT方法应用到实际地震信号的分析中，讨论其应用效果。在此基础上将经验模态分解阀值去噪方法，运用到合成地震道集的去噪中，验证了该去噪方法的有效性。

1HHT方法的原理

1.1经验模态分解

在进行HHT方法的时频分析之前，需要定义固有模态函数(IMF)。它必须满足两个方面的要求，①信号曲线过零点的数值和曲线的极值点数不能相差超过一个；②在任意一个局部范围内，极大值的包络线和极小值的包络线是关于时间轴近似对称的[3]。

经验模态分解就是将原信号分解为有限个不同尺度的模态函数，具体流程是：

1)找出原始信号x(t)所有的极值点，并将其用三次样条函数插值成为原数据序列的上包络线bmax(t)和下包络线bmin(t)，并求出其上包络线和下包络线的平均m1(t)。

(1)

2)将原数据序列减去平均包络后，得到一个新的数据序列。

h1(t)=x(t)-m1(t)

(2)

判断h1(t)是否为IMF函数，若不满足IMF条件，将h1(t)看作新的x(t)，重复上述处理过程，直到h1(t)满足条件时记c1(t)为IMF(1)：

c1(t)=h1(t)

(3)

然后令：

r(t)=x(t)-c1(t)

(4)

3)将看作新的x(t)，重复以上步骤1)和步骤2)，即可依次得到固有模态函数的各阶分量IMF(k)，直到满足给定的终止条件时筛选结束。终止条件为：

(5)

根据大量实践表明，迭代阈值SD设为0.2～0.3比较合适[3]。

4)原始的数据序列即可由这些IMF分量以及一个均值或趋势项r(t)表示。

(6)

也就是说分解得到的各分量可以通过简单相加得到原信号，所以EMD分解得到的IMF分量都是原信号固有的模态特征。

1.2瞬时分量和希尔伯特时频谱

将分解得到的每一阶IMF分量进行希尔伯特变换：

(7)

式中cpv代表柯西主值( Cauchy Principal Value)。

构造解析信号:

(8)

于是得到幅值函数：

(9)

相位函数：

(10)

进一步可以求出瞬时频率：

(11)

根据幅值函数和瞬时频率，定义原始信号为：

(12)

这种将信号幅度表示在时间和频率的平面上的分布就称为Hilbert时频谱，简称为Hilbert谱，用表示为：

(13)

式中ωj(t)=ω,Hilbert边际谱的定义为：

(14)

边际谱表示每个频率在时间上的累计幅值，在统计意义上就是将所有的数据进行时间上的累加。

2EMD分解阀值去噪

常规的去噪方法(如F-K滤波、小波变换、广义S变换等)，其理论都受傅立叶变换的限制，滤波效果都会受到滤波的通放带的影响。希尔伯特-黄变换是以瞬时频率为信号变化的基本量、特征模态为基本时域信号的一种新方法，不会像上述方法受傅立叶变换理论的约束，可以在全时段兼顾到频率分辨率和时间分辨率，具有很好的局部特性和自适应性，适用于非平稳信号的滤波和去噪。

在实际运用中，通常阀值是固定的：

(15)

式中：σ2为噪声的方差；N为采样的长度。但是通常获得精确的噪声方差是很困难的，所以在计算中，常常采用估算的方法对噪声方差进行计算。

(16)

式中：mae表示平均绝对误差；ch是IMF1的高频系数。这是因为ch是分解得到的最精细的系数，主要就是噪声系数。

3信号的EMD分解与时频分析

3.1合成信号的EMD分解

参考文献[6]中合成信号由一个调幅调频信号和一个正弦波叠加而成，其中调幅调频信号的基频 为50 Hz，其调制频率为20 Hz，正弦波的频率为120 Hz。

图1(a)所示为合成信号和分解得到的6阶IMF时间域波形曲线。第一行表示原始合成信号；IMF1表示一阶序列(c1(t))，是第一个分解出来的高频信号，对应于原始信号中的120 Hz正弦波；IMF2表示一阶序列(c2(t))，是第二个分解出来的信号，对应于原始信号中的50 Hz的调频调幅信号；IMF3、IMF4、IMF5、IMF6和r6分别代表三阶、四阶、五阶、六阶序列(c3(t)、c4(t)、c5(t)、c6(t))和剩余残量。根据EMD的分解原理，高频信号应该首先被分解出来，即120 Hz的正弦波应该是IMF1;其次应该是50 Hz的调幅调频信号，后面得到的IMF分量就是信号的趋势分量和残余信号了。这也证明了该方法的正确性和有效性。

3.2HHT时频变换和常规时频分析方法

对信号进行EMD分解后，将得到的所有IMF分量进行希尔伯特变换，再综合各阶瞬时频谱，就得到信号的HHT时频谱(图2)。

从图2(a)可看到两条红色曲线，分别代表了50 Hz为基频的调幅调频信号和120 Hz的正弦波。根据时频谱图可以看到，能量幅值随时间和频率是动态变化的，而且不同频率的细微不同也能区分出来。图2(b)所示为对应的HHT 边际谱，它是不同频率在整个信号时间内的能量积累。

图3(a)和图3(b)分别是短时傅立叶变换和平滑伪Wigner-Ville分布，可以看到，虽然这两种方法都可以分辨出50Hz和120Hz，但不能刻画出相应频率的波形变化特征。这也正是由于这两种方法都是基于傅立叶变换原理，不能进行局部的时频分析。

根据上面合成信号的时频分析，可以看到HHT方法相比传统方法具有很好的优越性，它不需要人为选择基函数，可以自适应地进行经验模态分解，得到的固有模态函数是原信号的固有信息，而且可以根据需要改变幅值，从而能够描述信号的非平稳程度。

3.3实测地震信号的EMD分解和时频分析

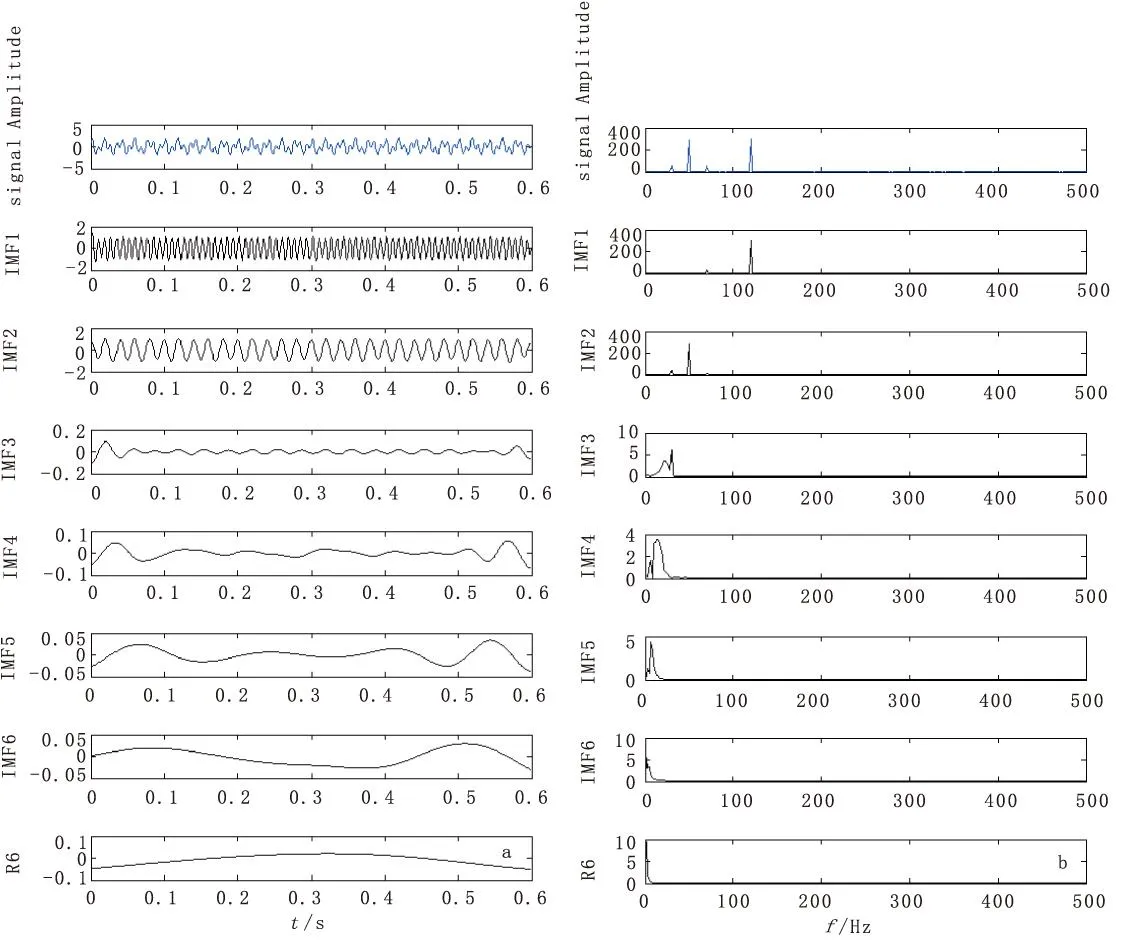
图1　合成信号的EMD分解及其频谱Fig．1　EMD decomposition and frequency spectrum of signal and IMF components(a)信号及6阶IMF时间域波形；(b)信号及6阶IMF的频谱

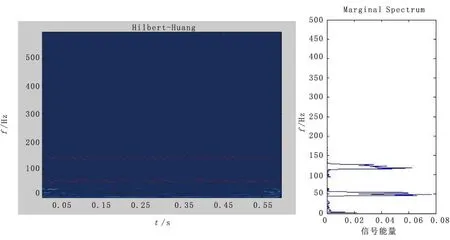
图2　合成信号的HHT时频谱Fig．2　HHT time-frequency spectrum of signal(a) 合成信号的二维HHT时频谱； (b) 合成信号的 HHT边际谱

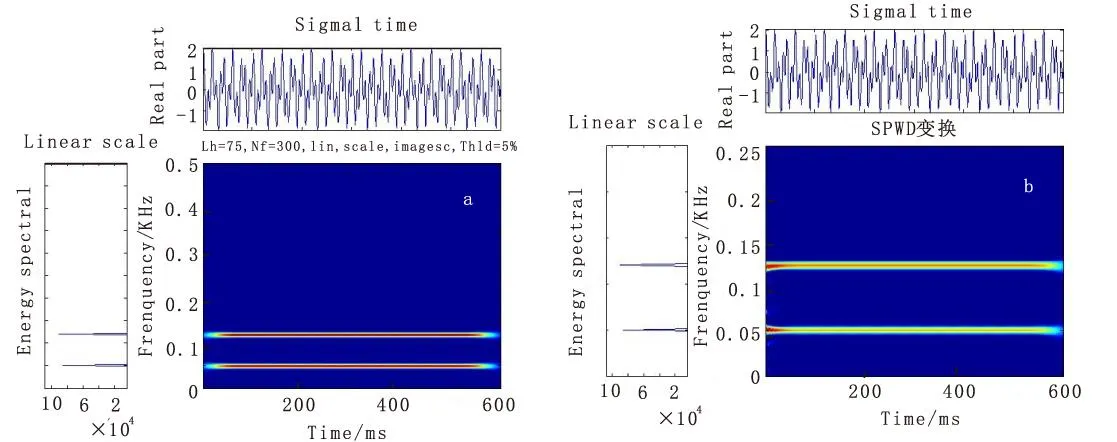
图3　合成信号的时频分析Fig．3　Time-frequency analysis of composite signal(a) 合成信号的短时傅立叶变换；(b) 合成信号的平滑伪Wigner-Ville分布

图4　实测地震信号Fig．4　Original seismic signal

实际地震信号产生的复杂性以及采集过程中的各种干扰原因，地震检波器获得的信号往往是非线性、非平稳的。图4是一个原始地震波形，采集时间间隔为0.001 s。通过HHT方法对该地震信号进行时频分析，以说明HHT方法的有效性和刻画信号非线性的能力。

图 5(a)所示为实测地震信号及经过EMD分解后的8阶固有模态函数(IMF)。由EMD的分解原理，可知各分量是按频率从高到低排列的，其中高频成分震动明显，可以用于初动检测；低频分量可以看作是简单的非线性变化，可以用来消除趋势干扰和进行相关的校正。图 5(b)所示为信号与各阶IMF的频谱，可见随着分解次数的增加，得到的IMF分量能量也逐渐减弱。由图5可见，整个记录的能量主要集中在30 Hz以内的低频成分，这是由于检波器在地表附近，而震源在地下几千米，经过地下介质的吸收衰减，只有低频信号能被检波器接收到。

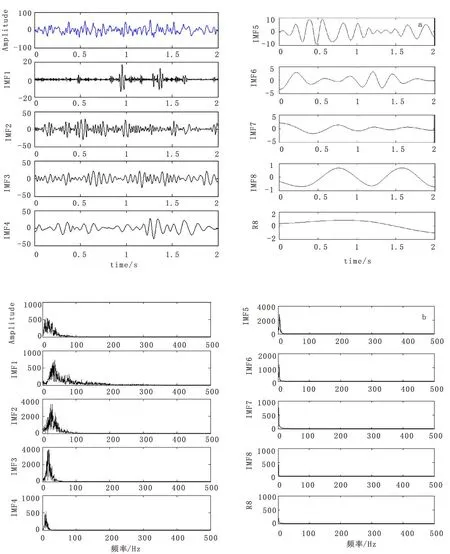
图5　地震信号的EMD分解及其频谱Fig．5　EMD decomposition and frequency spectrum of seismic signal and IMF components(a) 地震信号和8阶IMF时间域波形；(b)地震信号和8阶IMF的频谱

图7　地震数据的去噪Fig．7　The seismic data denoising(a)原始单炮记录；(b)F-K滤波结果；(c)EMD分解阀值去噪结果

图6是对图5(a)所示的所有IMF分量进行Hilbert变换得到的时频谱。图6(a)中的点、线表示能量变换特征的时频演化过程，线表示能量的聚集性较好，且颜色越明显，能量越大，反之，能量越小；点表示能量相对分散。由此可见，希尔伯特谱能很好地刻画出信号幅值在时间和频率上的变化情况，地震信号的非线性、非平稳特征都能很好的体现出来，在细微的变化上，能准确地表现出突变点的位置。图6(b)为地震信号的HHT边际谱，对应图6(a)中每个频率在信号持续时间内的能量积累，显然能量集中在0 Hz～30 Hz频段内，这与实际的采集情况是相吻合的。

由上述分析，说明HHT方法具有完全的自适应性，避免了人为选择基函数和窗函数的影响，而且其时频分辨率不受Heisenberg测不准原理的限制，具有完全的局部时频分析能力[8-10]。

4EMD分解阀值去噪效果测试

在地震资料的去噪中，需要对每一道地震信号进行EMD分解阀值去噪，然后将处理后的地震道进行叠加输出，就可以得到多道的单炮记录或者叠加剖面。图7(a)为实际的单炮记录，可以看到地震信号受面波干扰严重，其反射波与面波混叠，反射波的同相轴分辨困难，地震信号的信噪比较低。

相较于F-K滤波，EMD阀值去噪不仅压制了面波，加强了浅层信号的强度，使同相轴更加清晰，而且各个时频段的能量均没有大的损失，在单炮记录上每一道数据均能很好地显示。

5结论

1)运用EMD方法可以对信号进行自适应的分解，而且分解得到的每一个IMF分量都代表了原始信号的固有特征，因此可以选择不同的IMF进行时频分析，具有很好的灵活性。

2)HHT时频谱在地震信号的时频分析中，能够反映地震信号随时间和时频动态变化的主要特征，且时频分辨率不受Heisenberg测不准原理的限制，这为地震信号的识别、分析提供了有利条件。

3)HHT 时频谱的能量主要集中在一定的时间和频率范围内，而不是整个时频空间，这也真实反映了非线性、非平稳序列的本质特征。

4)HHT变换能够很好地反映出信号的局部特性，也就能够很好地反映出噪声的频率成分和范围，因此运用经验模态分解阀值能够很好地对信号进行时频滤波，去噪效果也比较理想。

[1]郑治真，胡劲波.瞬时频谱分析及其在地震趋势估计中的应用[J].地震学报，1993，15(l)：68-75.

ZHENG Z Z，HU J B.Instaneous spectrum analysis and its application in estimation of earthquake tendency[J].Acta Seismologica Sinica,1993，15(l)：68-75.(In Chinese)

[2]刘希强，周蕙兰，李 红. 基于小波包变换的地震数据时频分析方法[J].西北地震学报，2000，22( 2)：143-147.

LIU X Q，ZHOU H L，LI H.The time-frequency analysis method about seismic data based on wavelet packet transform[J].North-Western Seismological Journal,2000，22( 2)：143-147.(In Chinese)

[3]HUANG N E, SHEN Z, LONG S R, et al.The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.R.Soc.London,1998,454:903-995

[4]WU Z，HUANG N E．A study of the characteristics of white noise using the empirical mode decomposition method[J]．Proceedings of the Royal Society A，2004，460(2046)：1597-1611．

[5]Wu Z H，HUANG N E．Ensemble empirical mode decomposition：a noise-assisted data analysis method[J]Advances in Adaptive Data Analysis,2009，1(1)：1-41．

[6]武安绪,吴培稚,兰从欣,等.Hilbert-Huang 变换与地震信号的时频分析研究[J].中国地震，2005，21(2)：207-215.

WU A X, WU P Z, LAN C X, et al. Hilbert-Huang transform and time—frequency analysis of seismic signal[J].Earthquake Research in China, 2005, 21(2): 207-216.(In Chinese)

[7]汤井田,蔡剑华,任政勇,等.Hilbert-Huang 变换与大地电磁信号的时频分析研[J].中南大学学报，2009，40(5)：1399-1406.

TANG J T，CAI J H，REN Z Y，et al.Hilbert-Huang transform and time-frequency analysis of magnetotelluric signal[J].Journal of Central South University.2009，40(5)：1399-1406.(In Chinese)

[8]陈斌.时频分析及在地震信号分析中的应用研究[D].成都：成都理工大学,2007.

CHENG B.Time-frequency analysis and its implication in seismic signal[D].Chengdu: Chengdu University of Technology,2007.(In Chinese)

[9]杨培杰,印兴耀,张广智.希尔伯特黄变换地震信号时频分析与属性提取[J].地球物理学进展,2007,22(5):1585-1590.

YANG P J，YIN X Y，ZHANG G Z.Seismic signal time-frequency analysis and attributes extraction based on HHT[J].Progress in geophysics,2007,22(5):1585-1590.(In Chinese)

[10]黄光南.希尔伯特黄变换及其在地震资料分析处理中的应用[D].青岛：中国海洋大学,2009.

HUANG G N.Hilbert Huang transform and applications of it in seismic data analysis and processing[D].Qingdao: Ocean University of China,2009.(In Chinese)

Research on Hilbert Huang transform in time-frequency analysis of seismic signals

ZHOU Zhu-sheng， LUO Yong-tao*

(School of Geoscience and Info-Physics,Central South University,Changsha410083,China)

Abstract:With the development of time-frequency analysis, higher feasibility and accuracy on production has been required for complex signal. Firstly, the time-frequency analysis method of Hilbert-Huang transform and conception of transient frequency are introduced. The empirical mode decomposition and time?frequency distribution of a compound signal is carried on and then the actual seismic data were analyzed and processed based on Hilbert-Huang transform (HHT) spectrum. A time-frequency filtering method based on the transform is used by tasting on a synthetic seismic records example. The result proves its effectiveness.

Key words:Hilbert-Huang transform; empirical mode decomposition; seismic signals; time-frequency analysis； time-frequency filtering

中图分类号：P 631.4

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.01.09

文章编号：1001-1749(2016)01-0059-08

作者简介：周竹生(1965-)，男，博士，教授，主要从事资源勘察、工程地球物理勘探、应用软件研制及数据库开发等方面的教学和研究工作，E-mail：672390136@qq.com。*通信作者：罗勇涛(1990-)，男，硕士，主要从事工程地震勘探的研究，E-mail：1206387954@qq.com。

收稿日期：2015-01-16改回日期：2015-04-13