地图代数距离变换算法的改进及实现
2016-03-24刘列平
李 强,董 燕,刘列平,刘 艳
(1.昆明理工大学 国土资源与工程学院,云南 昆明 650093;
2.甘肃省地矿局测绘勘察院,甘肃 兰州 730060)
地图代数距离变换算法的改进及实现
李强1,董燕1,刘列平2,刘艳1
(1.昆明理工大学 国土资源与工程学院,云南 昆明650093;
2.甘肃省地矿局测绘勘察院,甘肃 兰州730060)
摘要为进一步提高地图代数距离变换算法的效率,详细分析了已有地图代数的欧氏距离变换算法,针对三个方面对已有算法进行改进,并且运用C++语言编写程序实现。该算法在增加较小存储空间的情况下,避免了行列号的排序查找,与已有算法进行了对比试验,证实该算法的效率较已有算法提高了约20%。
关键词地图代数;距离变换;算法
目前,距离变换分为基于数学形态学的距离变换和基于地图代数的距离变换。基于形态学的距离变换算法大多致力于算法效率和完全性上的研究,其算法扩展性十分有限[1]。地图代数的欧氏距离变换算法在距离部分没有误差,仅有的误差为实体栅格化的误差以及开方凑整的误差,它们均小于0.5个像元[2],该算法理论严密,算法简单、高效、精确,已成为实用化的技术,便于推广到三维及多维应用中[3]。欧氏距离变换的困难之一在于根号,而地图代数的距离变换去掉了根号,使用整数运算,效率较高[4]。
1地图代数距离变换算法
1.1算法简介
栅格平面上一栅格(i,j)到原点的欧氏距离为(i2+j2)1/2,其坐标值在栅格平面上均为整数,距离值与平方和值为映射关系,除少数点外,对于45°线下三角平面大部分是一一对应的。以45°线为对称轴镜像对称扩展为第一象限,再以坐标轴为对称轴扩展到其余三个象限,便形成栅格平方平面,并把只有一个实体在原点的栅格平方平面称为单位(栅格)平方平面。将各栅格中心点距原点欧氏距离的平方值记为D。每个栅格单元的D值需要根据周围的8个邻域栅格单元的D值来判断,这8个栅格单元的D值按图1所示依次标记为D1、D2、D3、D4、D5、D6、D7、D8[5-7]。在第一象限内,距离平方值之间有如下规律:
D1(i,j)=2D(i-1,j)-D(i-2,j)+2,
(1)
D2(i,j)=D(i-1,j-1)+2(i-1)+
2(j-1)+2,
(2)
D3(i,j)=2D(i,j-1)-D(i,j-2)+2。
(3)
在第二、三、四象限同样有相应的关系。
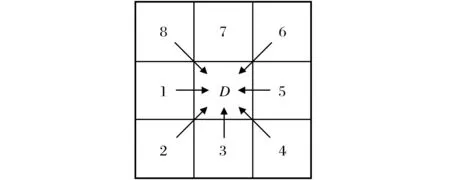
图1 8个栅格单元的D值标记Fig.1 Successive label of D value of 8 raster unit
据此其变换步骤为:
首先,赋所有实体点为0值,并赋所有非实体空间点为足够大的正数M;
其次,顺序访问,即行号由0,1,2…递增,列号由0,1,2…递增,按下式改写各点平方值:
D(i,j)=min(D1(i,j),D2(i,j),D3(i,j),
D4(i,j),D(i,j));
(4)
再次,逆序访问并改写各点平方值:
D(i,j)=min(D5(i,j),D6(i,j),D7(i,j),
D8(i,j),D(i,j));
(5)
最后,改写各点距离平方值为距离值。
1.2算法分析
平方平面内任一栅格的平方值均可从原点推算得到,因此可以顺序、逆序多次访问栅格,计算栅格的平方值。已有算法效率很高,但仍存在以下可改进之处:
(1)对于D1、D3、D5、D7的计算简单,但需要判断参与计算的两栅格平方值是否源于同一原点;
(2)计算D2、D4、D6、D8时需要D值及与其对应的行列号,此时需要对距离进行排序,并按D值查找行列号,消耗时间较长,且一个D值对应多个i,j时,判断较困难;
(3)一次顺、逆序访问并改写D值之后,仍有部分区域的D值不正确,需要再次顺序访问,如图2(以10×10的栅格为例,其中0代表实体点所在栅格)中阴影部分为错误区域,其他部分为正确区域。

图2 部分D值不正确区域Fig.2 Areas with partially incorrect D value
2算法改进
针对上述不足,研究时对算法做如下改进:
(1)计算方法方面。将式(1)改为
D1(i,j)=D(i,j-1)+2(j-1)+1,
(6)
式(3)改为
D3(i,j)=D(i-1,j)+2(i-1)+1。
(7)
根据类似的规律改进D5、D7值的计算,计算时只需一个栅格的D值及其所对应的行列号,因此不需要判定是否为同一原点。
(2)对于行列号,算法中设置一维结构体数组变量专门用于存储栅格的行列号,可节省排序查找行列号所消耗的时间,提高效率。由于顺序访问时只需计算D1、D2、D3、D4,因此只需记录当前处理行及其下方第一行栅格的行列号,逆序访问时也只需记录当前行与上一行,记录栅格行列号的数量只需要栅格宽度的2倍即可。
(3)在访问方式方面做了相应的改进,访问时遇到栅格D值为0或取D4时,从当前栅格逆向访问,返回后继续按原顺序访问。改进之后只需一次顺、逆序访问便可完成距离变换,不需再次访问。
具体的算法实现过程分以下四个步骤:
①赋所有空间点为一个足够大的正数M,赋所有实体点为0;
②顺序访问各栅格。将第一个栅格的行列号均设为0,顺序访问,列号由0,1,2…递增,行号由0,1,2…递增,分两种情况:如当前处理栅格值为0,则将其行列号均改写为0,然后逆向访问,计算并比较D(i,j)与D5(i,j)(此时只需计算右侧传递值),如D5(i,j)
③逆序访问。逆序访问时与顺序访问类似,只是行列号和计算方法略有不同,将所有栅格的初始行列号设为较大值,且行号与列号差值也较大,如行号为图像高2+图像宽2,列号设为2×(图像高2+图像宽2),行号向下为加,列号向左为加。由式(6)、式(7)可知,在行列号取传递值时,计算所得D值为所需值,而在取较大值时,会出现很小的负数,此时传递的值并非所需值。因此逆向访问时,所有计算所得D值均取其绝对值之后再比较,便可避免D值被此类错误值改写。逆向访问时也分为两种情况:如当前处理栅格值为0,行列号均改写为0,然后顺序访问计算并比较D1(i,j)与D(i,j)(此时只需计算左侧传递值),如D1(i,j)≤D(i,j),则改写其值及行列号,继续顺序访问,直至D1(i,j)> D(i,j)或至该行最右端时返回至该0点,继续逆序访问;如当前处理栅格值不为0,计算并比较D5(i,j)、D6(i,j)、D7(i,j)、D8(i,j),取其中最小值与D(i,j)比较,如不大于D(i,j),则改写当前栅格值,并由最小值所对应的行列号计算i,j的值,如果最小值为D8(即左上方向值最小),须顺序访问,其方法和停止规则同上,返回后继续逆序访问;
(4)改写距离平方值为距离值。
3算法的实现及分析
3.1算法的实现
研究在Microsoft visual studio2010的编译环境下运用C++语言编写程序,读取位图图像,使用改进后的算法,实现地图代数的欧氏距离变换,并输出变换后的图像,如图3所示。图3中(a)、(b)、(c)、(d)分别为点、线、面及点线面混合距离变换后的灰度图像,(e)、(f)、(g)、(h)分别为对应距离变换后距离值放大20倍的灰度图像,从图3中可清楚地看到距实体的等距线。

图3 距离变换结果Fig.3 Ditance changing result
3.2算法分析
该算法需顺序、逆序两次访问图像,顺序访问时遇到实体或传递值为右下角时需逆向访问,但只需访问至传递值小于当前值或至该行最左端时即停止,逆向访问时亦如此,顺、逆访问中,总返回访问的栅格数为N/H,其中:N为图像中包含原点(即栅格值为0)的行数;H为栅格图像的高度,因此其最大访问次数为2+N/H。
研究中设计多次试验,运用该算法分别处理不同大小及不同实体数量的栅格图像,并与已有算法做了对比,试验结果如表1所列(该数据是在Windows7系统、CPU主频为2.5 GHz、内存为2 GB的PC机上试验所得)。
从表1的试验数据可以看出,该算法运算耗时较已有算法有所减少,且其运算时间仅与栅格大小有关,而与原点的数量关系甚微。

表1 不同算法在不同条件下所需的运算时间
4结论
研究以地图代数的理论为基础,详细分析了已有的地图代数距离变换算法的不足,并对已有算法进行改进。该算法避免了已有算法对行列号的排序查找,而采用记录的方式,在少量增加存储空间的情况下,使已有算法时间效率提高了约20%,且运算所需时间只与栅格数据大小有关,而与原点数量关系很小。对于大幅栅格数据,亦能快速完成欧氏距离变换。
参考文献:
[1]张晓贺,翟亮,张志华.欧氏距离变换光栅扫描算法的改进及扩展[J].兰州交通大学学报,2012,33(1):102-104.
[2]夏兰芳,胡鹏,白轶多,等.基于地图代数的最小生成树实现方法[J].测绘科学,2008,33(1):141-143.
[3]王满,孙海燕.基于地图代数的缓冲区分析算法的研究[J].测绘信息与工程,2009,34(3):33-34.
[4]胡鹏,游涟,吴艳兰,等.地图代数[M].武汉:武汉大学出版社,2006.
[5]吴艳兰,胡鹏,王乐辉.基于地图代数的山脊线和山谷线提取方法[J].测绘信息与工程,2006,31(2):15-16.
[6]耿协鹏,杨传勇,胡鹏.基于地图代数距离变换的空间实体分布的聚集度分析[J].测绘科学,2006,31(2):86-87.
[7]黄培之.提取山脊线和山谷线的一种新方法[J].武汉大学学报:信息科学版,2001,26(3):247-252.
Improvement and Impelmentation of Distance Transformation Algorithm of Map Algebra
Li Qiang1,Dong Yan1,Liu Lieping2,Liu Yan1
(1.FacultyofLandResourceEngineering,KunmingUniversityofScienceandTechnology,Kunming650093,China;2.TheInstituteofSurveyingandMappingBureauofGeologyandMineralResources
ofGansuProvince,Lanzhou730060,China)
AbstractTo further enhance the efficiency of map algebra distance transform algorithm,the Euclidean distance transform algorithm of the existing map algebra was explicitly analyzed,and the existing algorithm was improved from three aspects;Also a program implementation was programmed with C ++ language.Under the condition of increasing smaller storage space,this algorithm avoided the sorting and searching of rank numbers,and after a comparison test with existing algorithms,it was confirmed that the efficiency of this algorithm was improved by about 20% compared to the old one.
Key wordsMap Algebra;Distance transform;Algorithm
中图分类号:P208
文献标志码:A
文章编号:1004-0366(2016)01-0035-04
作者简介:李强(1985-),男,宁夏隆德人,硕士,研究方向为GIS开发与应用.E-mail:panpanxiangce@163.com.
收稿日期:2015-02-02;修回日期:2015-05-17.
doi:10.16468/j.cnki.issn1004-0366.2016.01.009.
引用格式:Li Qiang,Dong Yan,Liu Lieping,etal.Improvement and Impelmentation of Distance Transformation Algorithm of Map Algebra[J].Journal of Gansu Sciences,2016,28(1):35-38.[李强,董燕,刘列平,等.地图代数距离变换算法的改进及实现[J].甘肃科学学报,2016,28(1):35-38.]
