Rad-伪投射模及其相关性质

刘冠楠

(兰州理工大学 理学院,甘肃 兰州　730050)



Rad-伪投射模及其相关性质

刘冠楠

(兰州理工大学 理学院,甘肃 兰州730050)

摘要给出了rad-伪投射模的概念,讨论了rad-伪投射模的一些等价关系,并证明了rad-伪投射模的商模以及其直和项仍为rad-伪投射模所需的条件,且证明了rad-伪投射模的一些相关性质。

关键词rad-伪投射模;rad-N-投射模;伪投射模

投射模是非常基础,同时也是非常重要的一种模类。一直以来,投射模及其推广都广泛地引起了国内外代数工作者的关注[1]。文献[2]中引入了soc-N-内射模的概念,并对soc-N-内射模的相关性质进行了研究。文献[3]中作者提出了其对偶概念rad-N-投射模,并证明了其相关性质。设M,N为右R-模,称模M是rad-N-投射模,若对任意的满同态δ∶N→K和同态f∶M→K,其中K为N/rad(N)的像,存在同态g∶M→N,使得f=δg。设M,A为右R-模,称模M为伪投射模[4],若对满同态g∶M→A,f∶M→A,存在同态h∶M→M,使得f=gh。文献[4-8]中讨论了伪投射模的相关性质。作为rad-N-投射模和伪投射模的真推广,我们引入了rad-伪投射模的概念,并研究了rad-伪投射模的一些性质。

以下所有的环R都是有单位元的结合环,而所有的模均为右R-模。设M为右R-模,我们用rad(M)表示M的根。设Ψ为右R-单模的类,对任意右R-模M,有

rad(M)=∩{Ker(h)|h∶M→φ,φ∈Ψ}。

若M=R,则记作J=J(R)=rad(R)。若N是M的子模,则记作N≤M。

定义1称模M为rad-伪投射模,若对任意满同态g∶M→A和f∶M→A,其中A为M/rad(M)的像。存在同态h∶M→M,使得f=gh。

定理2设M为右R-模,则下列条件等价:

(1)M为rad-伪投射模;

(2)对任意的满同态f∶M→K,rad(M)⊆Ker(f),f*∶HomR(M,M)→HomR(M,K),其中HomR(M,K)均为满同态,且满足f*α=fα,则f*是满的。

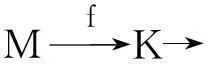
(⟸)因为rad(M)⊆Ker(f),所以K为M/rad(M)的像。由f*∶HomR(M,M)→HomR(M,K)是满的,对任意的满同态g∈HomR(M,K)可得,存在α∈HomR(M,M),使得f*α=fα=g,故M是rad-伪投射模。

定理3若M为右R-模,则下列条件等价:

(1)M是rad-伪投射模;

(2)对任意满同态,g∶N→L→0,N为M的任一满同态像,f∶M→L→0,其中L为N/rad(N)的像,则存在同态h∶M→N,使得f=gh。

证明(2)⟹(1)显然。

(1)⟹(2)任取满同态f∶M→L→0和g∶N→K→0,设K为M的一个子模,且N≅M/K,由

(K+rad(M))/K⊆rad(M/K)

以及

M/(K+rad(M))≅(M/K)/((K+rad(M))/K)

可得

M/rad(M)→(M/K)/((K+rad(M))/K)→

(M/K)/(rad(M/K))→L→0,

即L为M/rad(M)的像,M与N的交换图见图1。

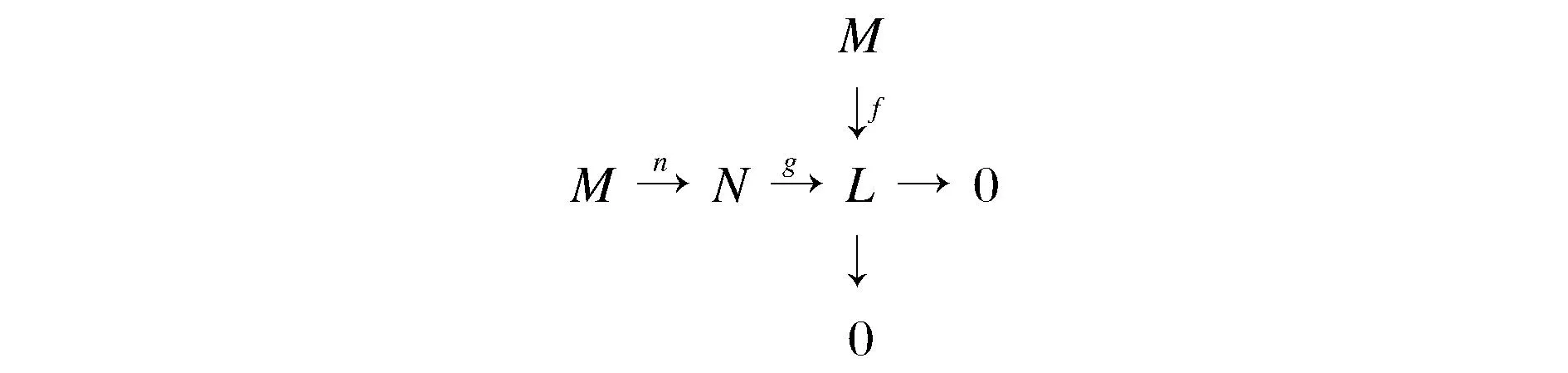
图1　M与N的交换图Fig.1　M and N exchange diagram

由N为M的一个满同态像可得,存在满同态η∶M→N→0,使得gη∶M→L→0为满同态,由M是rad-伪投射模可得,存在λ∶M→M使得f=gηλ,取h=ηλ∶M→N,则gh=gηλ=f。

推论4设M为rad-伪投射模,则对任意满同态,f∶M→N→0和g∶N→N→0,其中N为M/rad(M)的像,则存在h∶M→N,使得f=gh。

证明N与N的交换图见图2。

图2　N与N的交换图Fig.2　N and N exchange diagram

因为f∶M→N→0为满同态,则N为M的一个满同态像,根据定理3知,存在同态h∶M→N,使得f=gh。

证明设A是rad-伪投射模,A与B的交换图见图3。

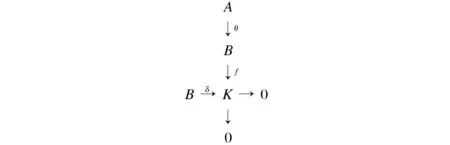
图3　A与B的交换图Fig.3　A and B exchange diagram

图3中K为B/rad(B)的同态像,由定理3知,存在λ∶A→B,使得δλ=fθ,取h=λθ-1∶B→B,则δh=δλθ-1=fθθ-1=f。即B是rad-伪投射模。

命题6若J(R)=0,则任意rad-伪投射模M为伪投射模。

证明M是rad-伪投射模,根为零的交换图见图4。

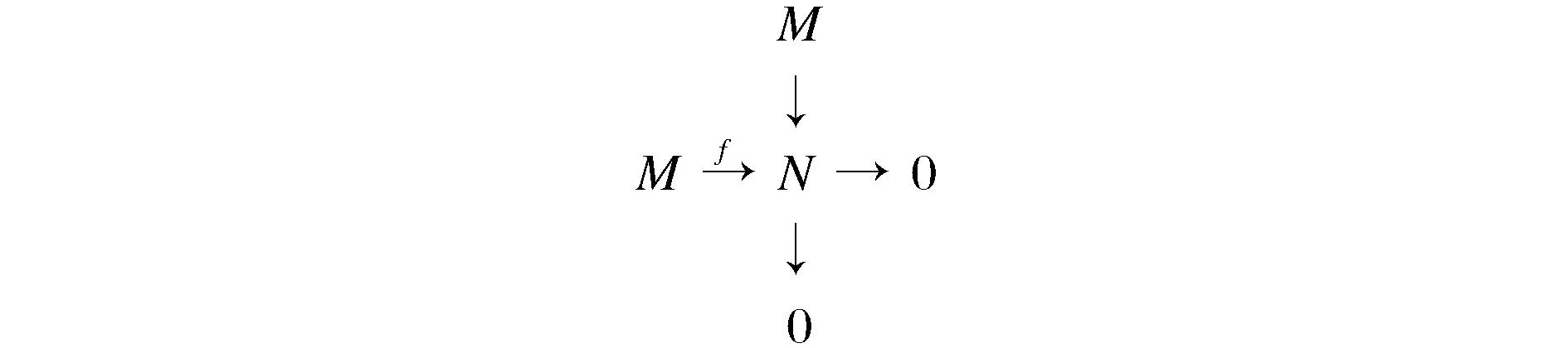
图4　根为零的交换图Fig.4　Zero roots exchange diagram

图4中N为M/rad(M)的像,故N≅(M/rad(M))/Ker(f)。令Ker(f)=K/rad(M),其中K≤M,rad(M)≤K,则N≅(M/rad(M))/(K/rad(M))⊆M/K。

因rad(M)=0,故f为任意满同态,即M是伪投射模。

命题7若M=⊕i∈IMi为rad-伪投射模,则Mi为rad-伪投射模。

证明关于直和的交换图见图5。

图5　关于直和的交换图Fig.5　Direct sum exchange diagram

图5中K为Mi/rad(Mi)的像。πi、μi分别为自然映射和自然嵌入,因为M为rad-伪投射模,所以由定理3可得,存在λ∶M→Mi,使得gλ=fπi,取h=λμi∶Mi→Mi,则gh=gλμi=fπiμi=f,因此Mi为rad-伪投射模。

命题8若Mi是rad-伪投射模,则⊕iMi(i=1,2,…,n)为rad-伪投射模。

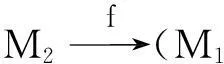
图6　正合列的交换图Fig.6　Exact sequence exchange diagram

图6中行和列都是正合的。

因rad(M1)⊆M1∩K=Ker(g),rad(M2)⊆(M1+K)∩M2,以及Mi(i=1,2)为rad-伪投射模,故可得如图7所示的Hom函子的交换图。

图7　Hom函子的交换图Fig.7　Hom functor exchange diagram

图7中行和列都是正合的、交换的。

M1为rad-伪投射模,M1与M1的交换图见图8。

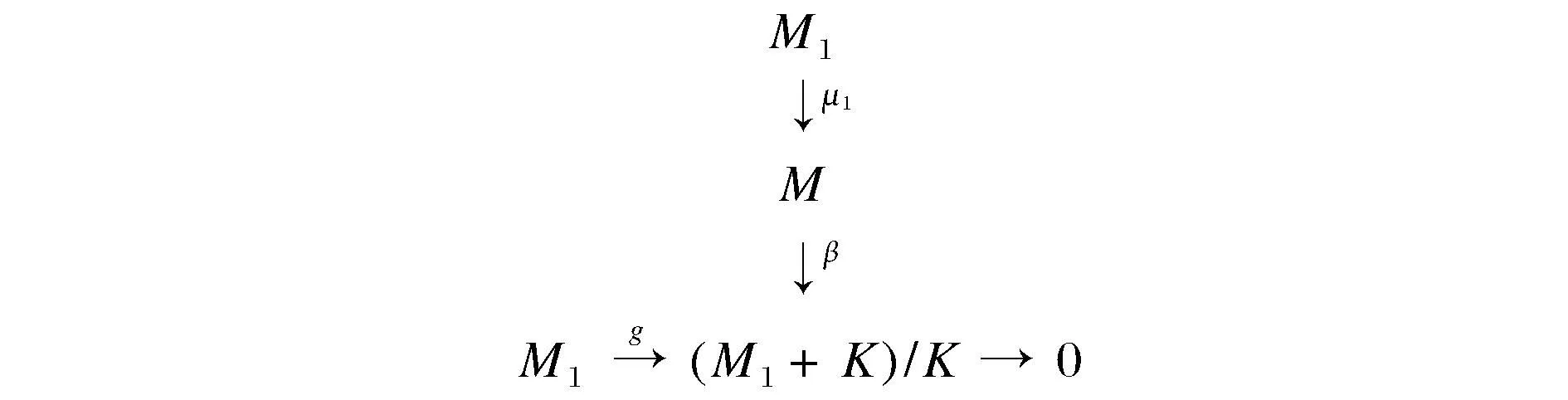
图8　M1与M1的交换图Fig.8　M1 and M1 exchange diagram

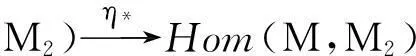
命题9设M,N为右R-模,若M⊕N为rad-伪投射模,则满同态f∶M→N,满足rad(M)⊆Ker(f)可裂。

证明可裂性见图9。

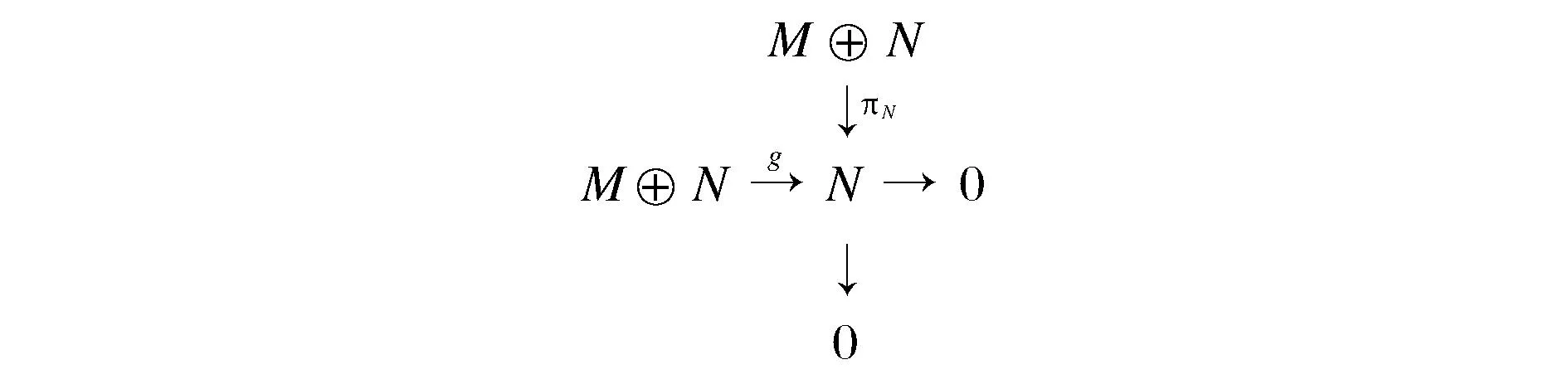
图9　可裂性Fig.9　Cleavability

图9中πM、πN为自然映射。定义满同态g=fπM∶M⊕N→N,g(m+n)=f(n),其中m∈M,n∈N,显然rad(M⊕N)=rad(M)⊕rad(N)⊆Ker(g),由M⊕N为rad-伪投射模得,存在λ∶M⊕N→M⊕N,使得gλ=πN。若η∶N→M⊕N为自然嵌入,定义θ∶N→M,θ(n)=πMλη(n)=πMλ(0+n),n∈N,则

fθ(n)=fπMλ(0+n)=gλ(0+n)=πN(0+n)=n,

即fθ=1N,故f可裂。

参考文献:

[1]Anderson F W,Fuller K R.Rings and Categories of Modules[M].2nded.北京:世界图书出版公司北京公司,2006.

[2]Amin I,Yousif M F,Zeyada N.Soc-injective Rings and Modules[J].Comm.Algebra,2005,33:4 229-4 250.

[3]Amin I,Ibrahim Y,Yousif M.Rad-Projective and Strongly Rad-ProjectiveModules[J].Comm.Algebra,2013,12:2 174-2 192.

[4]Tiwary A K,Pandeya M.Pseudo Projective and Pseudo Injective Modules[J].Indian J.of Pure Appl.Math.,1978,9(9):941-949.

[5]赵春娥,杜先能.关于伪投射模的若干讨论[J].大学数学,2006,22(3):100-102.

[6]Wakamatsu T.Pseudo-projectives and Pseudo-injectives in Abelian Categories[J].Math.Rep.Toyama Univ.,1979,2:133-142.

[7]俱鹏岳.纯伪投射模[J].甘肃科学学报,2010,22(3):18-19.

[8]Wisbauer R.Foundations of Module and Ring Theory[M].Philadelphia:Gordon and Breach,1991.

Pseudo-Projective Modules and Its Related Properties

Liu Guannan

(SchoolofSciences,LanzhouUniversityofTechnology,Lanzhou730050,China)

AbstractIn this paper,the concept of rad-Pseudo-Projective Modules is introduced,and and some of its equivalence relation are studied.It is proved that its quotient module and direct summand are still of great necessary in rad-Pseudo-Projective Modules and some related properties of rad-Pseudo-Projective Modules are demonstrated.

Key wordsRad-Pseudo-projective modules;Rad-N-projective modules;Pseudo-projective modules

中图分类号:O189.2

文献标志码:A

文章编号:1004-0366(2016)01-0032-03

作者简介:刘冠楠(1988-),女,辽宁鞍山人,硕士研究生,研究方向为基础数学.E-mail:373736451@qq.com.

收稿日期:2015-03-16;修回日期:2015-06-07.

doi:10.16468/j.cnki.issn1004-0366.2016.01.008.

引用格式:Liu Guannan.Pseudo-Projective Modules and Its Related Properties[J].Journal of Gansu Sciences,2016,28(1):32-34.[刘冠楠.Rad-伪投射模及其相关性质[J].甘肃科学学报,2016,28(1):32-34.]