功能梯度材料梁结构的稳定性分析

王　捷

(兰州理工大学 理学院,甘肃 兰州　730050)



功能梯度材料梁结构的稳定性分析

王捷

(兰州理工大学 理学院,甘肃 兰州730050)

摘要基于一阶剪切变形非线性梁理论,运用物理中面的概念推出功能梯度材料(FGM)梁稳定性问题的基本方程,分析了功能梯度材料梁在面内热荷载作用下的稳定性。分析中假设功能梯度材料性质只沿梁厚度方向、并按成分含量的幂指数形式变化;利用打靶法对所得方程进行数值求解。结果表明,两端夹紧的FGM 梁在均匀热载荷或非均匀热荷载作用下时都会发生过屈曲变形。

关键词功能梯度材料;屈曲;稳定性;打靶法

近年来,功能梯度材料(FGM,functionally graded materials)因其优越的性能在诸多领域都有广泛的应用。国内外许多学者对功能梯度材料梁的屈曲行为进行了研究。Birman等[1]介绍了功能梯度材料中的主要进展,包括颗粒材料的同质化、传热问题、稳定性和动态分析、设计和制造以及应用和断裂。Huang等[2,3]基于弹性力学平面问题的基本方程,假设应力函数是长度坐标的多项式函数,用弹性力学的方法推出了功能梯度各向异性悬臂梁在受到线性均布载荷作用时的解析解,同时假设热传导问题为沿厚度方向的一位热传导问题推出了在热载荷和非均匀载荷作用下的功能梯度各向异性悬臂梁的解析解。张靖华等[4]应用微分求积法(DQM,differential-quadrature method)分析了变截面功能梯度梁的弯曲。马连生等[5]基于一阶剪切变形梁理论,求出面内热载荷作用下梁过屈曲问题的精确解。文献[6]中利用相同的理论引用物理中面的概念导出了FGM 梁的基本方程,分析了热载荷作用下简支FGM 梁的弯曲行为。Ma等[7]推导了均匀面内热载荷作用下功能梯度梁的非线性静动态力学行为,并用打靶法数值的求解了控制方程,详细的讨论了材料常数、横向剪切变形、温度相关的材料特性、面内热载荷以及边界条件的影响。文献[8]中基于同样的理论基础,得到了面内热载荷作用下的功能梯度梁的非线性静态相应的精确解。研究基于一阶剪切变形非线性梁理论,并运用物理中面的概念推出FGM梁稳定性问题的基本方程,分析了功能梯度材料梁在面内热荷载作用下的稳定性。

1控制方程

考虑一个矩形截面的功能梯度材料梁,见图1。横截面面积为A,长为l,宽为b,高为h。笛卡尔坐标系(x,y,z)的坐标原点建立在梁的左端点。xoy平面为梁未变形时的中面,x轴与梁的形心轴一致,z轴正方向朝着横截面的顶点并垂直于x-y平面。

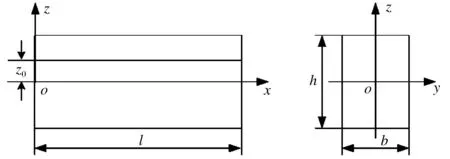
图1　功能梯度材料梁的几何模型Fig.1　Geometric model of beam of functionallygraded material

考虑金属和陶瓷功能梯度材料,材料属性P(如杨氏模量E、热膨胀系数等)沿着梁的高度变化,表达式为

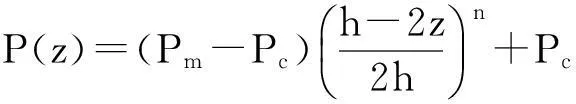
(1)

其中:下标m和c分别表示金属和陶瓷成分;n为梯度指数,表示该值时成分含量的功能梯度材料;泊松比取0.3。

功能梯度材料梁物理中面Z=Z0,有

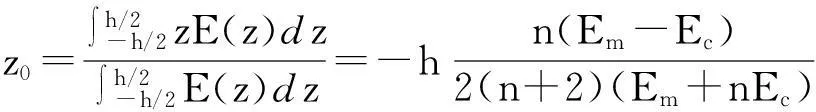
(2)

由一阶剪切梁理论和物理中面的概念位移函数具有如下形式:

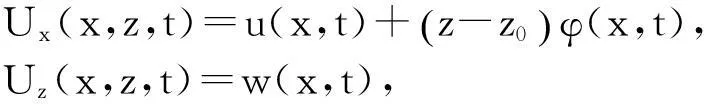
(3)

其中:w和u分别为物理中面上沿着坐标轴z和x方向的位移。

几何方程为

(4)

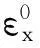
应力应变关系为

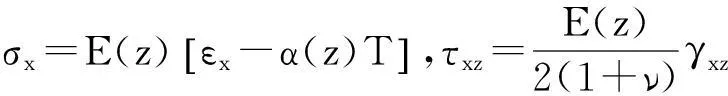
(5)

基于物理中面的功能梯度材料梁本构方程为

(6)

其中:

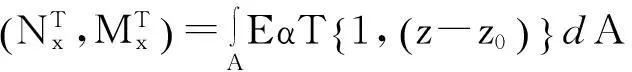
其中:ks为剪切修正系数,这里取3/2;T为梁的温度。

用能量法可得到如下位移形式平衡方程和边界条件:

(7)

边界条件:

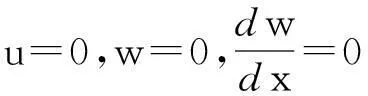
夹紧端引入无量纲量:

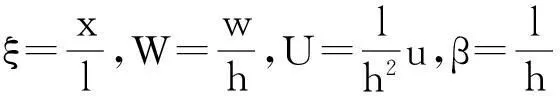
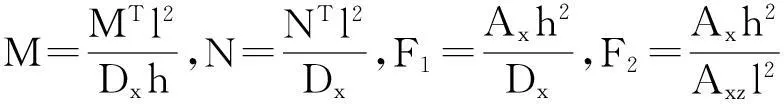
得到问题方程的控制方程

(8)

考虑上下表面温度不同,沿高度方向温度也呈梯度改变。假设温度T(z)满足一阶热传导方程

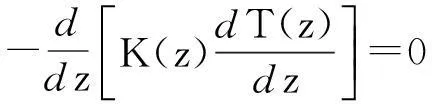
(9)

材料上表面为陶瓷,下表面为金属,温度边界条件如下:

T(h/2)=Tc,T(-h/2)=Tm,

(10)

其中:K(z)为热传导系数,满足物性参数方程

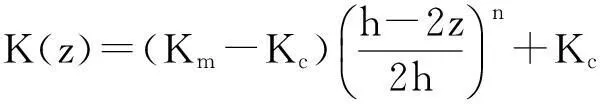
解得

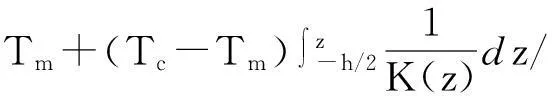
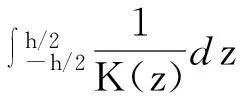
(11)

将K(z)按幂级数展开并带入式(11)得到

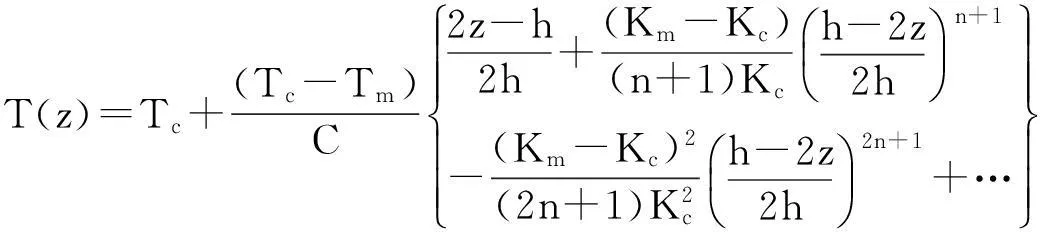
(12)

为了计算方便,取前5项进行计算[9]。利用打靶方法数值地求解相应边界条件下的方程,可得到梁过屈曲或弯曲的数值结果。

2数值结果与讨论

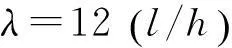
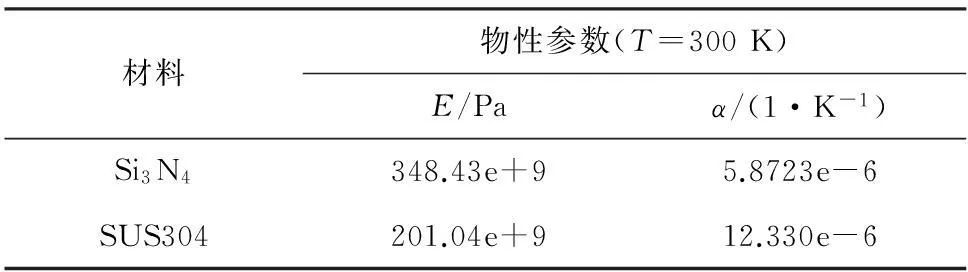
表1　Si3N4和SUS304的材料属性

2.1均匀温度载荷

两端夹紧功能梯度材料梁对于不同的梯度指数n在均匀温度下的典型热过屈曲路径如图2所示。图2表明其热过屈曲路径随n的增大而增大。

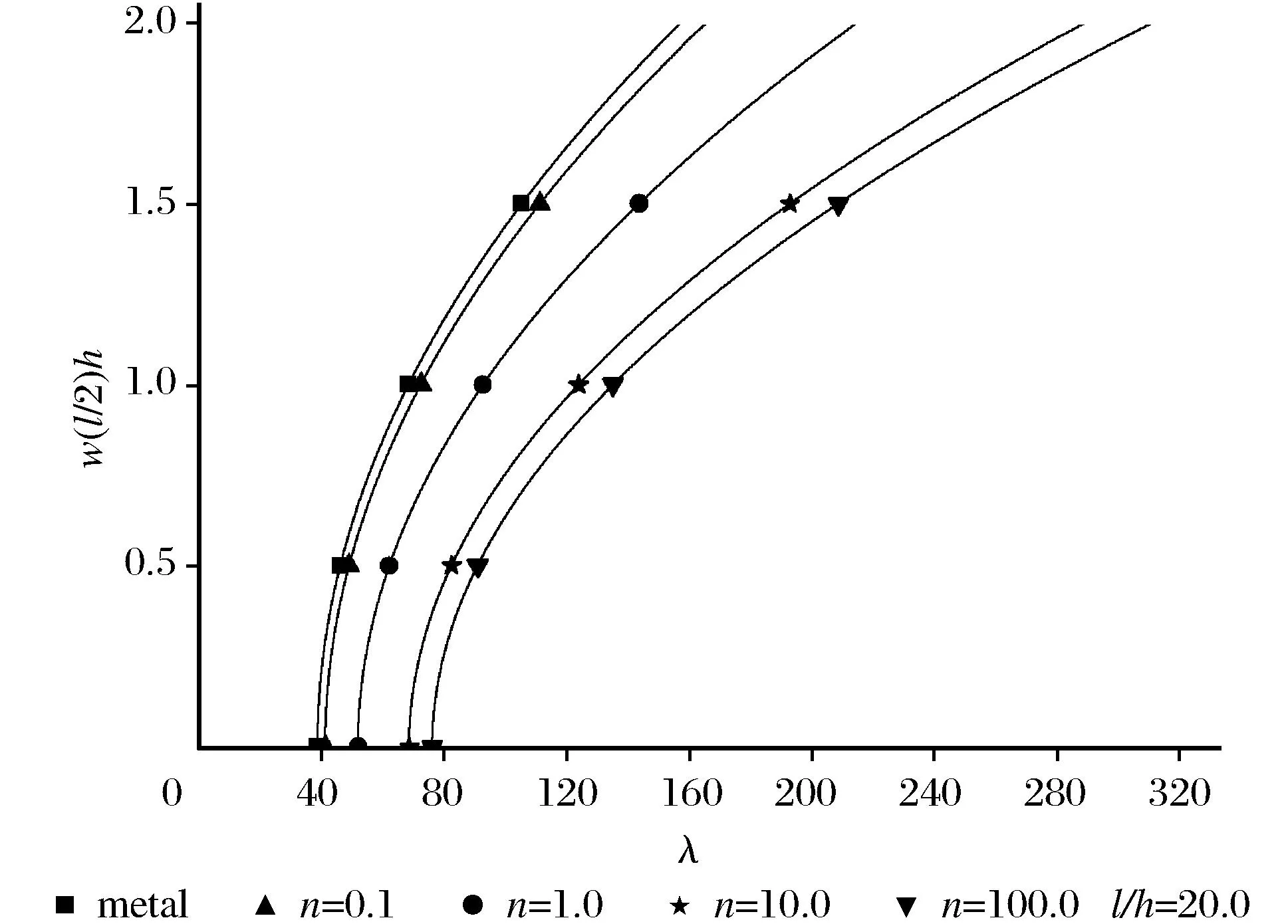
图2　均匀温度荷载下过屈曲路径Fig.2　Post-buckling path in presence of load atuniform temperature

图3为均匀温度载荷下临界热屈曲荷载λcr随着梯度指数n的变化。从图3可以清楚的看到在n的开始阶段无量纲临界屈曲载荷快速上升,当n较大时,临界屈曲载荷随着梯度指数n的增加缓慢增加。

图4给出了两端夹紧的FGM梁均匀温度下的临界屈曲载荷和l/h的关系,l/h取值范围为5~100。图像表明l/h趋于无穷大时其对临界载荷影响不再明显。

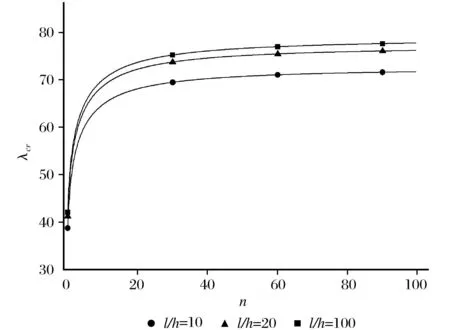
图3　临界屈曲载荷和梯度指数曲线Fig.3　Curves of critical buckling load and gradient index

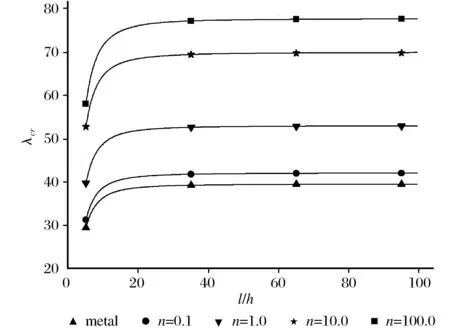
图4　临界屈曲载荷和l/h的关系Fig.4　Relationship between the criticalbuckling load and l/h

2.2非均匀温度载荷

图5给出了两端夹紧的FGM梁非均匀温度下的无量纲临界热屈曲荷载λcr随着梯度指数n的变化。从图5可以清楚的看到,在梯度指数n的开始阶段无量纲热屈曲载荷有一个急剧的先下降再上升的过程,这与均匀面内热载荷作用时的情况有着明显的不同。

不同的梯度指数n两端夹紧功能梯度材料梁非均匀温度下的典型热过屈曲路径如图6所示。图7给出了两端夹紧的FGM梁非均匀温度下临界屈曲载荷和Tc/Tm的关系。从图6可以看出非均匀面内热载荷作用时纯金属的热过屈曲路径曲线不再位于最左边,而是介于中间,这与均匀温度载荷作用时的热过屈曲路径有着明显的不同,这是因为非均匀面内热载荷作用时临界热载荷随梯度指数n的变化并不和均匀面内热载荷作用时一样,而是先减小后增大。

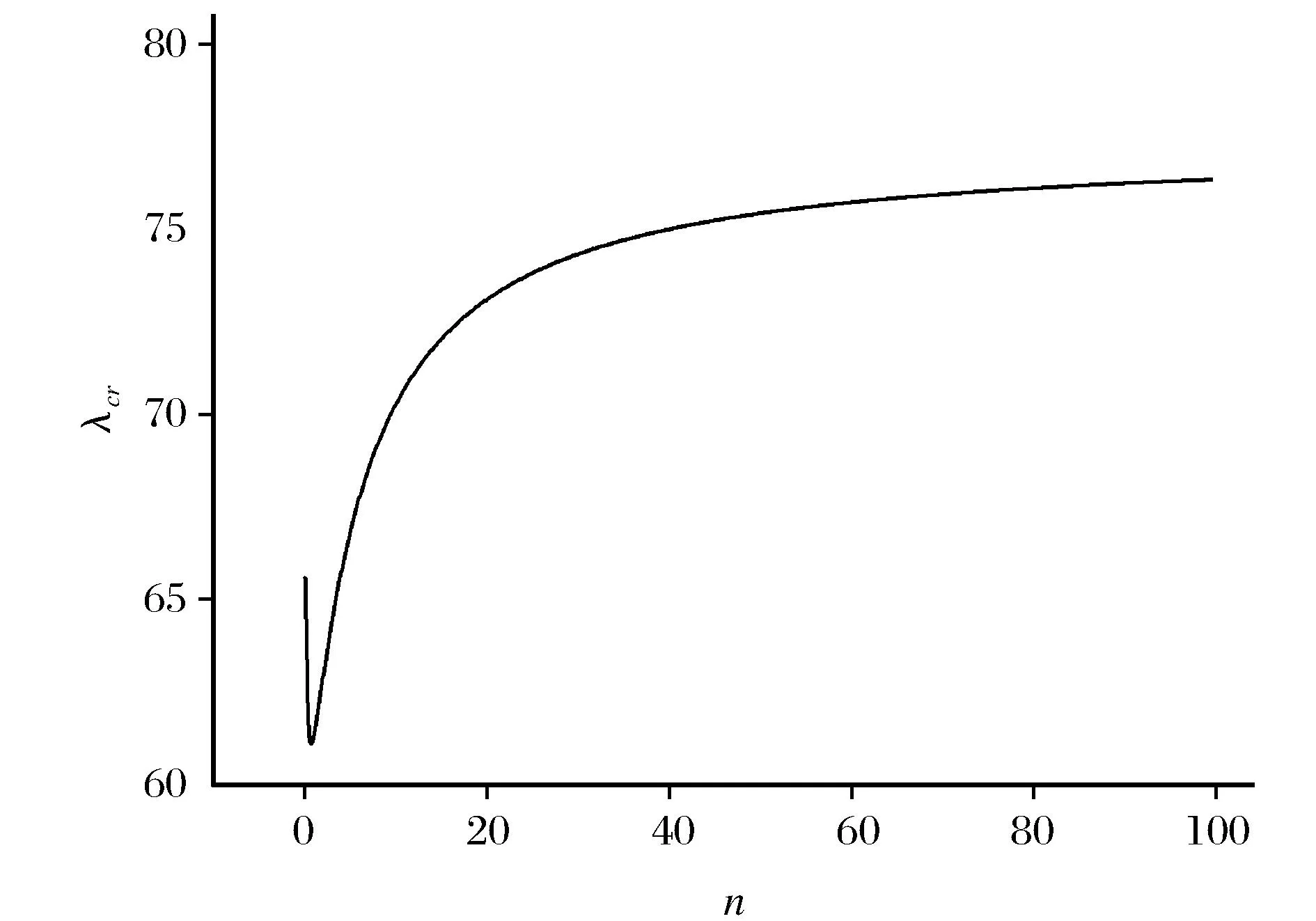
图5　临界屈曲载荷和梯度指数曲线Fig.5　Curves of critical buckling load and gradient index

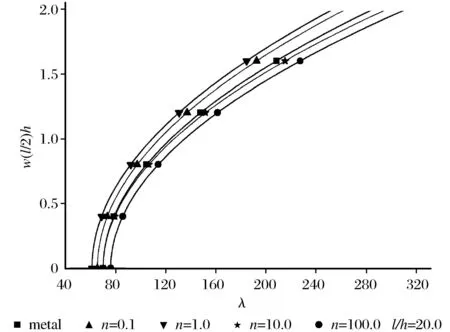
图6　非均匀温度荷载下过屈曲路径Fig.6　Post-buckling path in presence of loadat uneven temperature

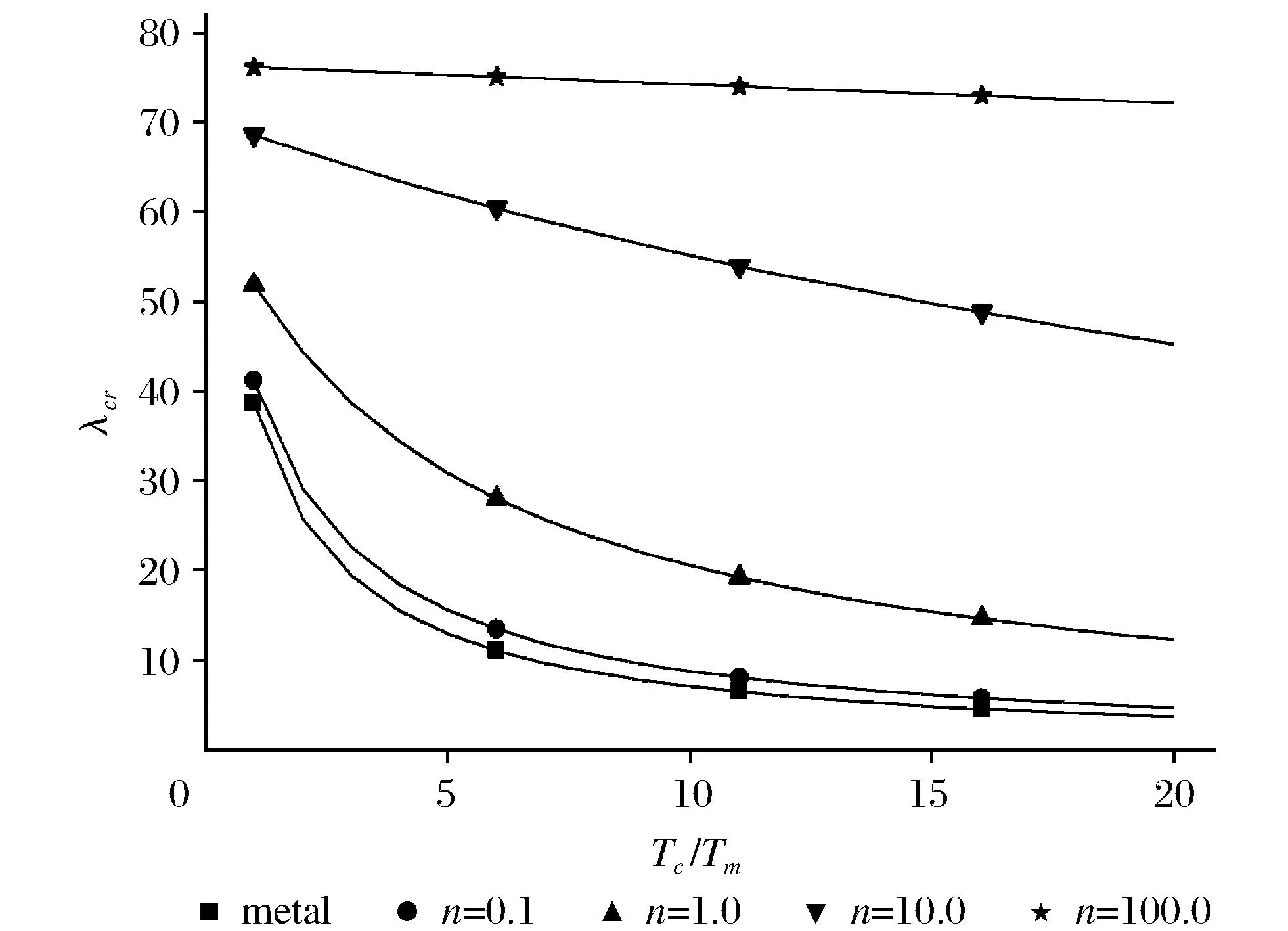
图7　临界屈曲载荷和Tc/Tm的关系Fig.7　Relationship between the critical buckling load and Tc/Tm

3结论

将坐标面建立在物理中面上,基于一阶剪切非线性梁理论,利用物理中面概念导出了功能梯度材料(FGM)梁稳定性问题的基本方程。研究了在均匀热载荷和非均匀热荷载作用下固支FGM梁的稳定性问题。得出以下结论:

(1)均匀与非均匀面内热载荷作用下两端夹紧功能梯度材料梁都显示出了典型的热过屈曲行为特征。也就是说,当热载荷如果没有达到临界屈曲载荷时,FGM 梁不会产生横向挠度,而将保持原来的平直状态。

(2) 两端夹紧的功能梯度材料梁无量纲临界屈曲载荷随着功能梯度指数n的增大而增大,而梁的转角却在减小。

(3) 夹紧FGM梁的过屈曲变形受横向剪切变形影响明显,这种影响随着长细比的增大而降低,直至趋于经典结果。

参考文献:

[1]Birman V,Byrd L W.Modeling and Analysis of Functionally Graded Materials and Structures[J].Applied Mechanics Reviews,2007,60(5):195-215.

[2]Huang D J,Ding H J,Chen W Q.Analytical Solution for Functionally Graded Anisotropic Cantilever Beam Subjected to Linearly Distributed Load[J].Applied Mathematics and Mechanics(English Edition),2007,28(7):855-856.

[3]Huang D J,Ding H J,Chen W Q.Analytical Colution for Functionally Graded Anisotropic Cantilever Beam under Thermal and Uniformly Distributed Load[J].Journal of Zhejiang University SCIENCE A,2007,8(9):1 351-1 355.

[4]张靖华,龚云,李世荣.微分求积法求解变截面功能梯度梁的弯曲问题[J].甘肃科学学报,2010,22(1):14-17 .

[5]马连生,顾春龙.剪切可变形梁热过屈曲解析解[J].工程力学,2012,29(2):172-176.

[6]马连生,牛牧华.基于物理中面FGM 简支梁的弯曲行为[J].应用力学学报,2010,27(3):590-593.

[7]Ma L S,Lee D W.A Further Discussion of Nonlinear Mechanical Behavior for FGM Beams under In-plane Thermal Loading[J].Composite Structures,2011,93:831-842.

[8]Ma L S,Lee D W.Exact Solutions for Nonlinear Static Responses of a Shear Deformable FGM Beam under an In-plan e Thermal Loading[J].European Journal of Mechanics A/Solids,2012,31:13-20.

[9]Wu L H.Thermal Buckling of a Simply Supported Moderately Thick Rectangular FGM Plate[J].Composite Struetures,2004,64(2):211-218.

Stability Analysis of Beam Structure of Functionally Graded Material

Wang Jie

(SchoolofSciences,LanzhouUniversityofTechnology,Lanzhou730050,China)

AbstractThe fundamental equation about the stability problem of beam of the functionally graded material (FGM) was deduced by using concept of physical surface on basis of non-linear beam theory for first-order shearing and deformation; and the stability of the beam of the functionally graded material in presence of thermal load in the surface was analyzed.During analysis,it was supposed that the property of the functionally graded material might be changed only along the direction of thickness and according to the form of power exponent of the component content of the component; and the value was obtained from the equation acquired by using the shooting method.The numerical result showed that the FGM beam with two ends held tightly might be subjected to post-buckling deformation under the action of even thermal load or uneven thermal load.

Key wordsFunctionally graded materials;Buckling;Stability;Shooting method

中图分类号:TB301

文献标志码:A

文章编号:1004-0366(2016)01-0012-05

作者简介:王捷(1990-),男,重庆涪陵人,硕士研究生,研究方向为新型材料结构的力学行为.E-mail:903506616@qq.com.

基金项目:国家自然科学基金:功能梯度材料结构的非线性稳定性理论研究(11472123)；功能梯度材料结构非线性力学行为的进一步研究(11072100).

收稿日期:2015-01-16;修回日期:2015-04-09.

doi:10.16468/j.cnki.issn1004-0366.2016.01.003.

引用格式:Wang Jie.Stability Analysis of Beam Structure of Functionally Graded Material[J].Journal of Gansu Sciences,2016,28(1):12-15,54.[王捷.功能梯度材料梁结构的稳定性分析[J].甘肃科学学报,2016,28(1):12-15,54.]