基于Vague集模糊值线性序法的雷达抗干扰效能评估

宋宝军，张　秦，姜　军

（空军工程大学防空反导学院，西安　710051）



基于Vague集模糊值线性序法的雷达抗干扰效能评估

宋宝军，张秦，姜军

（空军工程大学防空反导学院，西安710051）

摘要：针对已有评估方法存在的不足，提出了一种基于Vague集模糊值线性序法的雷达抗干扰效能评估方法。分析了影响雷达抗干扰效能的指标因素，给出了各评价指标的模糊值表示，建立了基于Vague集模糊值线性序法的雷达抗干扰效能综合评价模型，得到了评价其效能的排序方法。最后通过实例分析验证，该方法评估结果准确，具有一定参考价值。

关键词：Vague集，模糊优先矩阵，抗干扰，效能评估

0　引言

雷达的抗干扰效能是其综合能力的重要组成环节。因此，对抗干扰效能进行评估就显得尤为重要。目前，研究复杂电磁环境下雷达抗干扰效能评估方面的文献比较多［1 -4］，但大部分文献在进行模糊评估时具有一定的缺陷，通常会产生较大计算误差，且对相似度高的方案无法做出准确判断。

由于Vague集理论具有较强模糊信息表达能力，它不仅包含肯定支持度，同时还包含否定和弃权程度。所以，对于不精确数据的描述较传统模糊评价法更加科学有效，近年来在不确定多属性模糊评估问题中应用越来越广泛［5-8］。

为此，提出一种基于Vague集模糊值线性序法的雷达抗干扰效能评估方法，该方法能有效提高评估的客观性和准确性，进而提供更可靠的决策支持。

1　 Vague集基本理论

Vague集理论是由Gau和Buehrer在1993年提出的，它较传统的模糊集而言，是一种更加符合人类思维的新型理论。由于Vague集具有更强的模糊信息表达能力，在描述不确定数据时更加自然有效，它不仅包含肯定信息，同时还可包含否定和弃权信息。因此，越来越多学者将其应用于多属性模糊决策中。具体定义如下：

定义［9 - 10］设论域x=［x1，x2，…，xn］，X上一Vague集A分别由真隶属函数tA和假隶属函数fA描述，即tA：x→［0，1］，fA：X→［0，1］，其中，tA（xi）是由支持xi的证据所导出的肯定隶属度的下界，fA（xi）是由反对xi的证据所导出的否定隶属度的下界，且tA（xi）+fA（xi）≤1。元素在Vague集A中的隶属度被区间值vA（xi）=［tA（xi），1-fA（xi）］所界定，称vA（xi）为xi在A中Vague值，简写作V=［t，1-f］。

2　雷达抗干扰效能综合评价指标分析

在现代电子对抗环境下，雷达将面临来自多方面的威胁与干扰。由于雷达的抗干扰效能主要受其自身工作特性以及外部电磁环境特征的影响，现将雷达抗干扰效能评价体系概括为两个主要方面共计5个指标［11 -14］，第1个方面别为雷达自身特性，包括：探测信号平均功率、工作频段以及所采取的抗干扰措施3个指标，第2个方面为外部环境特征，包括：电磁对抗环境和干扰对抗时机两个指标。

雷达抗干扰效能综合评价指标体系如图1所示。

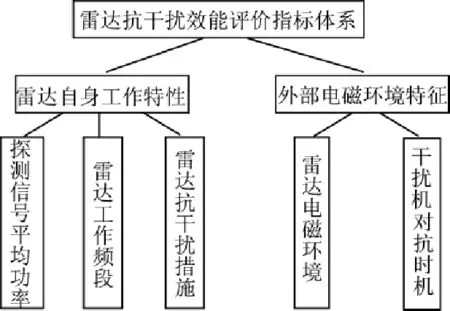
图1雷达抗干扰效能综合评价指标体系

2.1探测信号平均功率

实时信干比是衡量干扰强度的一项重要指标。因此，利用实时信干比值可以体现雷达的抗干扰能力，实时信干比越大说明雷达抗干扰能力越强。

由于实时信干比等于进入雷达接收机的回波信号功率与外部干扰信号功率比值。因此，当被探测目标与外部干扰功率不变时，探测信号平均功率的大小就直接影响了雷达接收机的回波信号功率，进而影响雷达干扰对抗效能。

现用探测信号平均功率系数U1来体现探测信号平均功率指标。

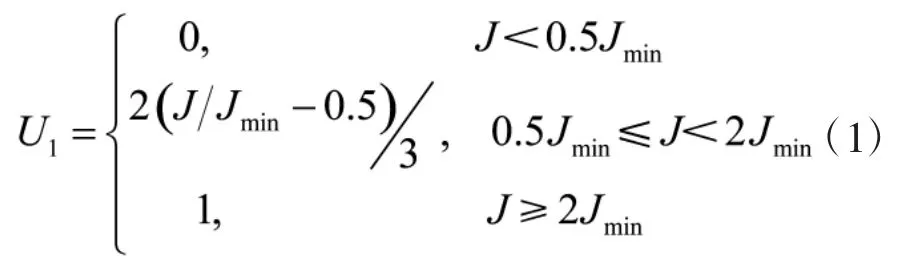
式（1）中，J为实时信干比，Jmin为雷达满足正常目标检测的最小信干比，U1越大，说明雷达抗干扰效能越好。

2.2雷达工作频段

由电磁信号接收理论得知，干扰信号频段与雷达工作频段的重合情况决定了干扰效能的好坏，重合度越低则干扰效果越差，雷达抗干扰效能越好。

现用频率重合系数U2来反映工作频段对雷达抗干扰效能影响。

式（2）中，［FJL，FJH］为干扰信号的频率区间，［FRL，FRH］为干扰信号的频率区间，频率重合系数U2越小，说明雷达抗干扰效能越低。

2.3雷达抗干扰措施

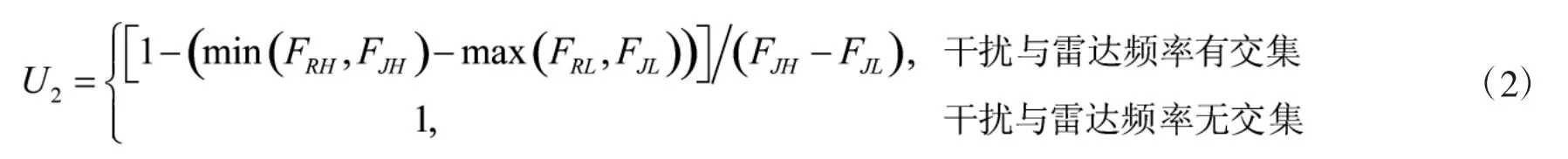
一般地，当雷达具备较多抗干扰技术时，通常具备较好的抗干扰效能。

因此，使用抗干扰技术系数U3来体现雷达抗干扰措施的使用情况对抗干扰效能提升的贡献。

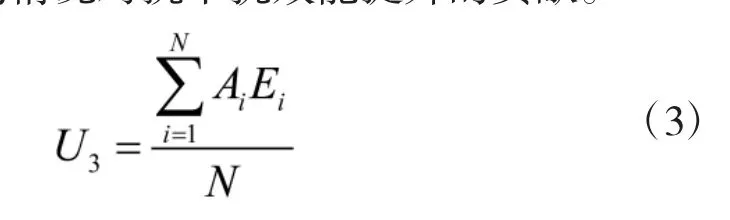
式（3）中，N为现有的所有抗干扰措施总和，Ai表示某部雷达是否具有第i项抗干扰技术措施，Ai=1代表具有抗干扰技术措施，否则Ai=0，Ei为第i项抗干扰技术措施在这部雷达中的效能，且有Ei∈［0，1］。

2.4电磁对抗环境以及干扰对抗时机

当外界的电磁环境越复杂时，雷达的抗干扰效能就越差。

现用电磁环境系数U4来描述电磁对抗环境对抗干扰效能影响，U4越大，表示雷达抗干扰效能越差。

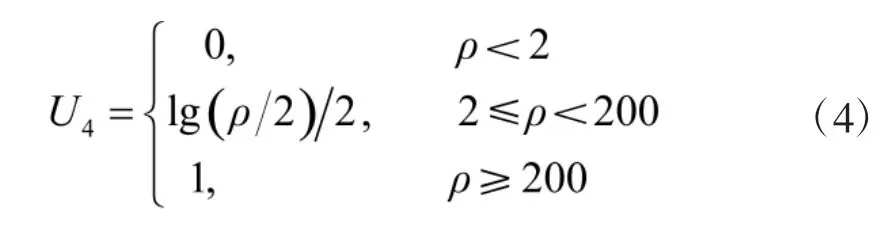
式（4）中，ρ为信号流密度（万个脉冲/s）。

外界干扰源在雷达的不同任务以及工作模式下的干扰效果是不同的。例如，同样强度与样式的干扰在雷达目标搜索或目标跟踪阶段的干扰影响是不同的，在雷达跟踪目标时，更容易受到干扰的影响而导致雷达效能降低。现用干扰时机因子U5来衡量干扰时机的不同对雷达抗干扰效果的影响。U5介于0~1之间，其越大就表明干扰时机对雷达越不利，此时雷达的抗干扰效能较差。

3　基于Vague集模糊值线性序法的雷达抗干扰效能评估方法

3.1评价指标的模糊值表示

假设有m部待评价的雷达，即有方案X={X1，X2，…，Xm}。以上5个评价指标分别为U1，U2，U3，U4，U5。各指标的权重记为w1，w2，w3，w4，w5，且w1+w2+w3+w4+w5=1。首先采取以下方法对各指标进行规范化处理。

对于效益型指标，令

对于成本型指标，令

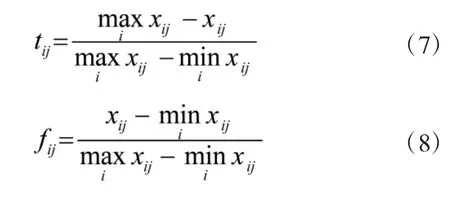
通过以上规范化处理，待评价方案Xi在第j （j=1，2，3，4，5）个评价指标Uj下的指标值用Vague值表示为vij=［tij，1-fij］。i=1，2…，m；j=1，2，3，4，5各指标的模糊值可按如下公式计算得到［13］：

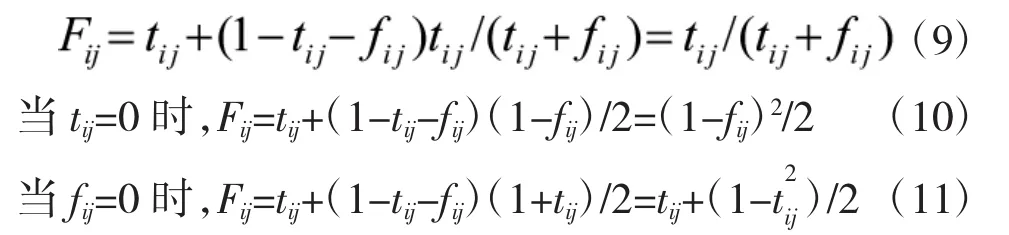
由此，可构成模糊值矩阵F=（Fij）m×n。

3.2基于Vague集模糊值线性序法的雷达抗干扰

效能评估方法

1）根据式（5）~式（8）对评价指标进行规范化，再根据式（9）~式（11）将各评价指标的Vague值转化为模糊值，构成模糊值矩阵F=（Fij）m×n。

2）构造模糊值线性序

对模糊值矩阵F中某一列d，对应指标Ud，模糊值为Uid，i=1，2…，m；j=1，2，…，5。按如下方法对各方案进行排序。

①若Fi1d＞Fi2d，则方案Xi1排在方案Xi2前面。

②若Fi1d=Fi2d，那么如果ti2d＞ti1d，则方案Xi1排在方案Xi2前面。

③若Fi1d=Fi2d，且ti1d=ti2d，那么如果（1-fi1d）＞（1-fi2d），则方案Xi1排在方案Xi2前面。

其中i1，i2=1，2，…，m。对模糊值矩阵F中每一列按数值大小对各方案进行排序，形成5个线性序，分别记为L1，L2，…，L5。

3）构造模糊优先矩阵

构造方案集X中的模糊优先矩阵Q为：

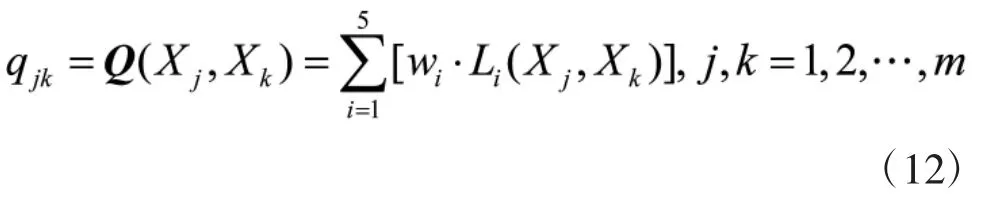
其中，

4）方案排序

取λ=0.5对模糊优先矩阵Q进行截割，得到截矩阵Qλ。令Mi表示Qλ中第i行中取值为1的元素个数，并按Mi（i=1，2…，m）的大小对各方案进行排序，即元素1的个数越多，对应的方案越优。

4　实例分析

假设有4种不同类型的待评价雷达，记为X= {X1，X2，X3，X4}。每部雷达抗干扰性能的优劣都要通过考察以上5个评价指标，即指标集U={U1，U2，U3，U4，U5}。各雷达在每个指标下的评价值见表1，各指标在［0，1］区间内取值。

所有参加评价专家结合这4部雷达各自的工作环境、技术特点、探测能力、信号接收能力、跟踪精度与分辨力等方面因素，进行综合评判后，给出评价指标U1，U2，U3，U4，U5的权重分别为：w1=0.20，w2=0.15，w3=0.45，w4=0.10，w5=0.10。

4.1构造模糊值矩阵F

根据第2节指标分析可知，指标U1，U2，U3为效益型指标，U4，U5为成本型指标。故可根据式（5）~式（8）对其进行规范化，这样可得到各指标的Vague集表示。

X1={（U1，［0.91，0.91］），（U2，［0.00，0.00］），（U3，［1.00，1.00］），（U4，［0.00，0.00］），（U5，［0.00，0.00］）}

X2={（U1，［0.72，0.72］），（U2，［1.00，1.00］），（U3，［0.79，0.79］），（U4，［1.00，1.00］），（U5，［0.93，0.93］）}

X3={（U1，［0.00，0.00］），（U2，［0.85，0.85］），（U3，［0.00，0.00］），（U4，［0.80，0.80］），（U5，［1.00，1.00］）}

X4={（U1，［1.00，1.00］），（U2，［0.80，0.80］），（U3，［0.93，0.93］），（U4，［0.40，0.40］），（U5，［0.07，0.07］）}

由此，根据式（9）~式（11）可得到模糊值矩阵

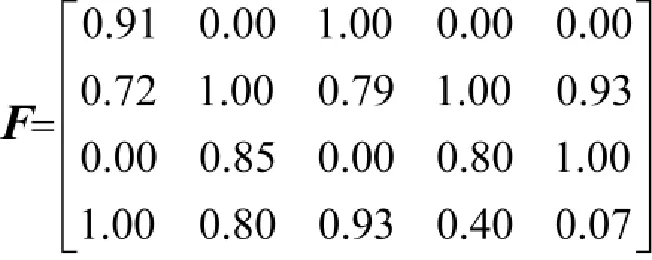
4.2构造模糊值线性序

对模糊值矩阵F中每一列按数值大小对各方案进行排序，形成5个序分别记为L1，L2，L3，L4，L5。

L1（按指标U1排序）：X4，X1，X2，X3；

L2（按指标U2排序）：X2，X3，X4，X1；

L3（按指标U3排序）：X1，X4，X2，X3；

L4（按指标U4排序）：X2，X3，X4，X1；

L5（按指标U5排序）：X3，X2，X4，X1。

4.3构造模糊优先矩阵Q

根据以上5个线性序，再将各指标权重代入式（12），可得模糊优先矩阵Q为：

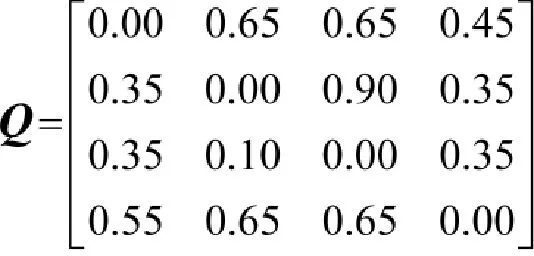
4.4方案排序

取λ=0.5对模糊优先矩阵Q进行截割，得到截矩阵Qλ。

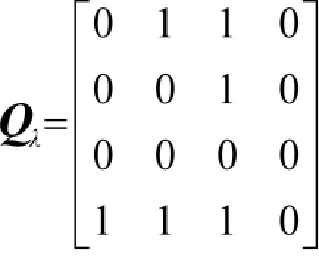
所以M1=2，M2=1，M3=0，M4=3由此可得各方案的排序为X4，X1，X2，X3。

实例证明，该结果符合多方专家的综合评判、得到了参评专家认可，并且与雷达设备在实际使用中表现相似。因此，用此种方法可以简单、快速地得到具有较高可信度的评估结果。

5　结论

为解决战场复杂电磁环境下的雷达抗干扰效能评估指标体系不易确定，评估过程中有用信息易被忽略，导致评估结果随机性较强，对特定电磁环境下雷达抗干扰效能的评价不客观、不准确等问题。本文给出了在复杂电磁环境下评价雷达抗干扰效能的指标体系，提出一种基于Vague集模糊值线性序法的雷达抗干扰效能评估方法，实例证明该方法简单、有效，通用性强，在雷达抗干扰效能的评估方面有着较为广泛应用前景。

参考文献：

［1］李浩，邱超凡，赵小亮.雷达抗干扰效能的多层次模糊评估方法［J］.雷达科学与技术，2012，10（2）：143-149.

［2］刘旭，李为民，吴晓东.雷达雷达抗干扰性能多层次灰色评估模型研究［J］.现代防御技术，2011，39（6）：179-184.

［3］易咸煜，孙闽红，唐斌.基于TOPSIS法的雷达抗烦扰措施优化选取［J］.现代雷达，2009，31（10）：35-37.

［4］魏保华，孟晨，范书义，等.基于变权模糊综合评判的雷达抗干扰性能评估［J］.现代雷达，2010，32（9）：15-18.

［5］夏璐，邢清华，范海雄. Vague物元及熵权的空袭目标威胁评估［J］.火力与指挥控制，2009，37（2）：84-88.

［6］要瑞璞，沈惠璋.不确定多属性Vague集决策方法［J］.计算机工程与应用，2010，46（14）：48-49.

［7］YE J. Improved method of multicriteria fuzzy decision making based on vague sets［J］.Computer-Aided Design，2007，（39）：164-169.

［8］HUANG K C，YANG G K. An enhanced method and its application for fuzzy multi-criteria decision making based on vague sets［J］.Computer-Aided Design，2008，（114）：103-113.

［9］王洪剑.基于Stribeck摩擦模型的系统模糊滑模控制［J］.四川兵工学报，2013，32（7）：113-115.

［10］耿涛，卢广山，张安.基于Vague集的空中目标威胁评估群决策方法［J］.系统工程与电子技术，2011，33（12）：2686-2690.

［11］UYTTENDAELE M，EDEN A，SZELISKI R. Eliminating ghosting and exposure artifacts in image mosaics［C］//Proceeding s of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Hawaii，2001.

［12］杨作宾，龚锐，刘光明，等.基于BP神经网络的火控雷达抗干扰效能评估［J］.现代防御技术，2010，38（1）：9-12.

［13］李浩.BP神经网络在雷达抗干扰能力评估中的应用［J］.中国雷达，2011（4）：1-4.

［14］要瑞璞，沈惠璋.Vague集多指标决策的模糊值线性序法［J］.计算机工程与应用，2009，45（28）：39-40.

Anti- jamming Effectiveness Evaluation Technology Research of Radar Based on Vague Sets and Fuzzy Liner Ranking

SONG Bao-jun，ZHANG Qin，JIANG Jun
（School of Air and Missile Defense，Air Force Engineering University，Xi’an 710051，China）

Abstract：Considering the deficiency of known evaluation technology of radar anti -jamming effectiveness，a new method based on vague sets and fuzzy liner ranking is presented. The indexes that affect Anti -jamming effectiveness of radar were analyzed，fuzzy value expression of indexes were offered，gave the comprehensive evaluation model of radar anti -jamming effectiveness based on vague sets and fuzzy liner ranking，and received the ranking method. Finally，via an example，the result of this assessment technology is correct and valuable.

Key words：vague set，fuzzy priority relation matrix，anti-jamming，effectiveness evaluation

作者简介：宋宝军（1982-），男，河北唐山人，讲师。研究方向：雷达抗干扰、雷达信号处理。

收稿日期：2015-01-09

文章编号：1002-0640（2016）02-0124-04

中图分类号：TN97

文献标识码：A

修回日期：2015-03-01