改进幂指数趋近律的航空发动机模糊滑模控制

田虎森，谢寿生，苗卓广，2，王　磊，3，任立通

（1.空军工程大学航空航天工程学院，西安　710038；2.解放军95961部队，北京　100195；3.解放军93704部队，北京　101100）



改进幂指数趋近律的航空发动机模糊滑模控制

田虎森1，谢寿生1，苗卓广1，2，王磊1，3，任立通1

（1.空军工程大学航空航天工程学院，西安710038；2.解放军95961部队，北京100195；3.解放军93704部队，北京101100）

摘要：针对滑模变结构控制趋近运动不具有鲁棒性的问题，提出了一种基于改进幂指数趋近律的航空发动机模糊滑模控制策略。采用一种参数模糊自调节的时变滑模面，“主动迎上”系统状态轨迹，而不是被动等待系统状态轨迹落在滑模面上，缩短趋近运动时间，提高控制器的鲁棒性；并提出了一种改进的幂指数趋近律，进一步削弱抖振。仿真结果表明，所设计的控制器取得了令人满意的控制效果，能有效地抑制干扰和参数不确定性的影响，削弱抖振。

关键词：航空发动机，鲁棒性，滑模变结构控制，趋近律，抖振

0　引言

现代航空发动机是融合气动、热力、机械、电子等众多子系统的复杂耦合的动力学系统，其控制系统性能的优劣将直接影响发动机及飞机的性能［1-3］。由于航空发动机工作范围宽广，参数变化范围大，实际系统中不可避免地存在着大量的干扰与未建模动态等不确定性，要求其控制系统要有很强鲁棒性。见文献［4-14］。

上述方法都有各自的优点，但是它们对到达滑模面之前的趋近运动关心较少，对于大多数滑模控制来说，趋近运动是不可忽略的过程。趋近运动的快慢不仅会影响系统响应速度，还会影响到刚进入滑模面时抖振的剧烈程度。由上述可知，缩短趋近运动时间，使系统状态尽快到达滑模面相当于提高了控制器的鲁棒性。因此，对趋近运动的研究意义不亚于对滑模面和控制律的研究意义。为此，本文基于模糊时变滑模面和改进幂指数趋近律的航空发动机滑模控制对滑模变结构控制的趋近运动进行了研究。

1　一类参数模糊自调节的时变滑模面设计

考虑如下的多变量系统数学模型为

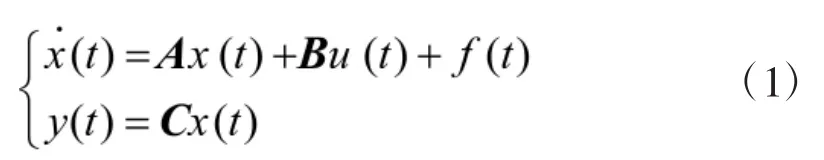
式中x（t）∈Rn，u（t）∈Rm，y（t）∈Rm，f（t）∈Rl分别为被控对象的状态向量、控制向量、输出向量及包含不确定性和外界干扰的等效干扰；A∈Rn×n，B∈Rn×m，C∈Rm×n分别为适当维数的矩阵。

定义系统误差e（t）=yr（t）-y（t），式中y（t）为系统的输出，yr（t）为y（t）的期望值。

定义如下滑模面函数

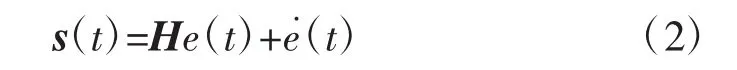
式中s（t）=［s1，s2，…，sm］T，H=diag［h1，h2，…，hm］，hi＞0，i=1，…，m，si= hiei+i。滑模面斜率hi不是固定不变的，而是由模糊控制器调节输出［15］。

设模糊控制器的输入量误差ei的基本论域为［-xei，xei］，误差变化率i的基本论域为，输出量的基本论域为（0.1，xhi］。上述输入变量和输出变量的基本论域内的量都是精确量，需要将其模糊化。

选择模糊控制器的输入量为误差ei和误差变化率i，输入量语言值（亦可称为模糊状态）取为

{PB（正大），PS（正小），ZR（零），NS（负小），NB（负大）}

模糊控制器的输出量为滑模面斜率hi，输出量语言值取为

{VB（非常大），B（大），M（一般），S（小），VS（非常小）}

把模糊输入变量hi分别进行归一化处理，得到如下相同的输入变量模糊子集论域

X={-1，-0.5，0，0.5，1}

输出变量hi的模糊子集论域选择如下

Y={0.1，0.5，1.45，50}

则基本论域和模糊子集论域之间关系分别由以下公式确定：

实际上式（3）和式（4）表示了由基本论域到模糊集论域的变换，这种变换也是一种映射，即由基本论域中任意一点映射到模糊集论域中相近的整数点。

模糊输入变量和输出变量都采用三角形隶属度函数，隶属度函数曲线如图1~图3所示。模糊控制规则如表1所示。

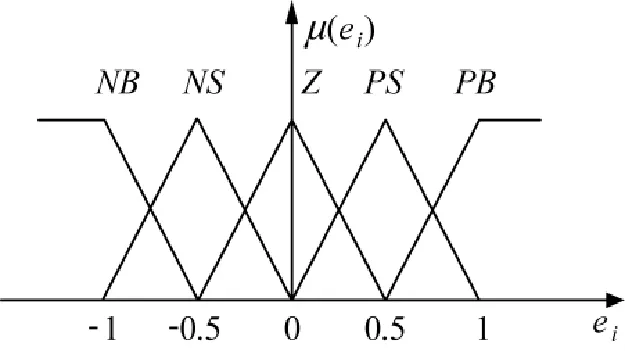
图1模糊控制器输入误差ei隶属函数

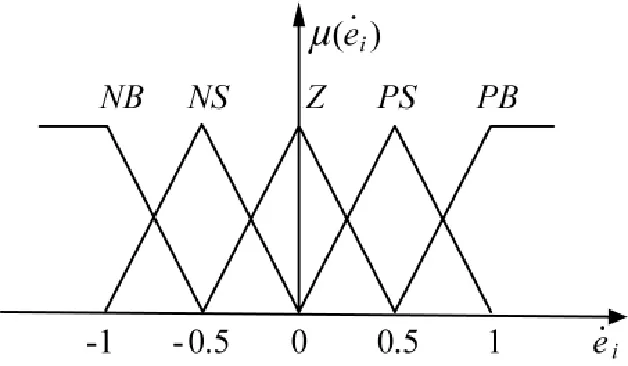
图2模糊控制器输入误差变化率i隶属函数

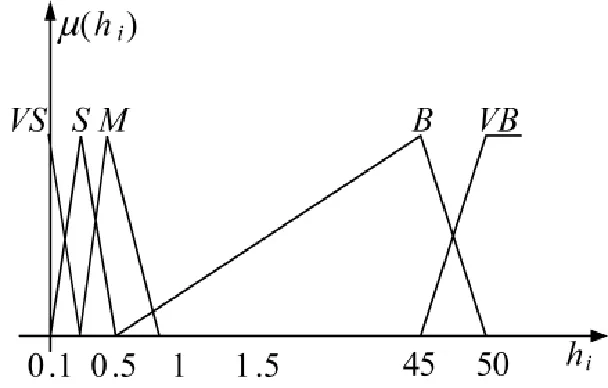
图3模糊控制器输出滑模面斜率hi隶属函数

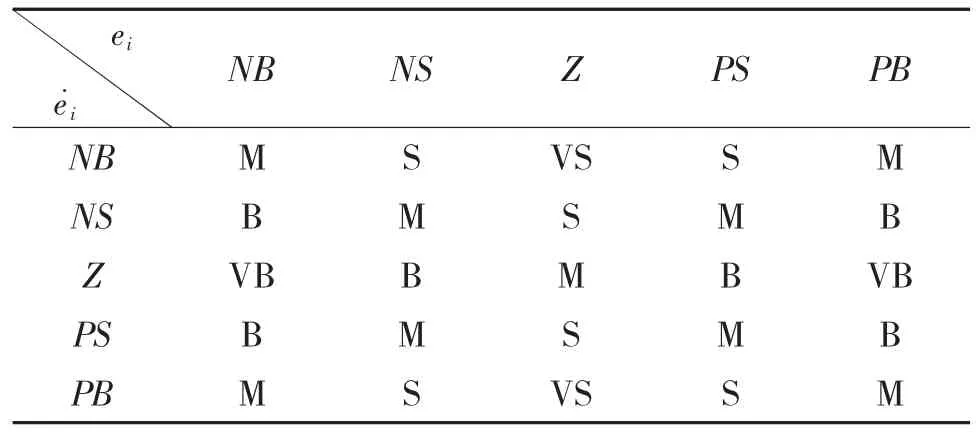
表1滑模面斜率hi模糊控制规则表

利用表1推理得到滑模面斜率的模糊量后需要进行反模糊化才能用到实际系统中去。反模糊化的方法很多，最常用的有最大隶属度法、取中位数法和重心法。相对于前两种方法，重心法既综合利用了模糊集信息，计算量又不是很大。因此，本文采用重心法对输出模糊量进行反模糊化。

2　改进的幂指数趋近律

系统从任意初始状态趋向切换面，直到到达切换面的运动称为趋近运动，即趋近运动为s→0的过程。根据滑模变结构控制原理，滑模可达性条件仅保证由状态空间任意位置运动点在有限时间内到达切换面的要求，而对于趋近运动的具体轨迹未作任何限制。趋近律方法是滑模变结构控制的一种典型控制策略，这种方法不仅可以对系统在切换面附近或沿切换面的滑模运动段进行分析，而且可以有效地对系统趋近段的动态过程分析和设计，从而保证系统在整个状态空间内都具有良好的运动品质。采用趋近律的方法可以改善趋近运动的动态品质。趋近律约束了到达滑模面前的运动方式，它除了影响系统响应速度的快慢，还会影响滑模运动的抖振程度。目前，常用的趋近律方法是指数趋近律［11］，对于连续系统，指数趋近律为

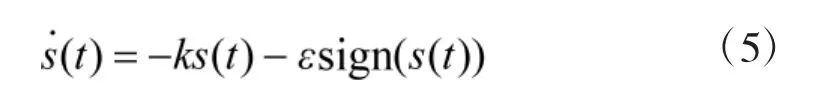
其中ε＞0，k＞0。

式（5）的指数趋近律具有以下特点：

①趋近速度从较大值逐步减小到零，不仅缩短了趋近时间，而且使运动点到达切换面时的速度较小；

②当切换函数s（t）趋近于零时，趋近速度是ε而不是零，可以保证有限时间到达。

但对于指数趋近律式（5），要有效抑制高频颤动，必须取较小的ε，而小的ε又影响了快速性；增大k可以加速趋近速度，但又要求系统有较大控制强度。

为克服指数趋近律缺点并兼顾其优点，本文提出了一种如下形式的改进幂指数趋近律：

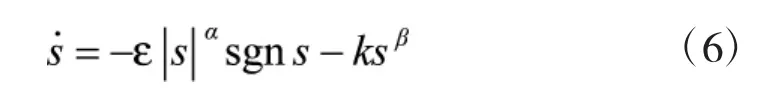
式中ε＞0，k＞0，1＞α≥0，β为正奇数。

当α=0，β=1时，改进的幂指数趋近律即为式（5）的一般指数趋近律。即式（5）的表达式为式（6）的一个特例。

滑动模态的存在是滑模变结构控制设计的前提。接下来分析式（6）改进幂指数趋近律是否满足滑动模态的存在条件和到达条件。

2.1存在条件分析

滑动模态的存在条件是滑模变结构控制应用的前提。如果系统的初始点x（0）不在s=0附近，而是在状态空间的任意位置，此时要求系统的运动必须趋向于切换面s=0，即必须满足到达条件，否则系统无法启动滑模运动。滑动模态存在条件的数学表达式为

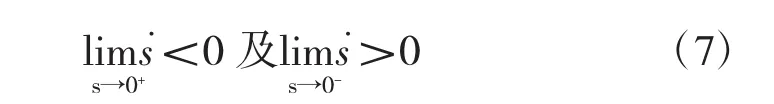
式（7）意味着在切换面领域内，运动轨线将于有限时间内到达切换面，故式（7）也称为局部到达条件。

考虑以下表达式：

式（8）中ε＞0，k＞0，1＞α≥0，β为正奇数，当s→ 0+时，-εαsgns-ksβ＜0，因此，。

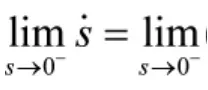
通过以上分析可知，本文提出的改进幂指数趋近律满足滑动模态存在条件。

2.2到达条件分析

滑模变结构控制的控制策略多种多样，对于滑动模态到达条件的实现形式也不尽相同。一般来讲，到达条件的等价形式为

其中切换函数s（x）应满足以下条件：①可微；②过原点，即s（0）=0。

由于状态变量x可以取任意值，即x可以离切换面任意远，故到达条件式（10）为全局到达条件。式（10）表示成Lyapunov函数的形式为

其中V（x）为定义的为Lyapunov函数，当式（11）成立时，则系统将最终到达并保持在滑模切换面s=0上。

考虑以下表达式：

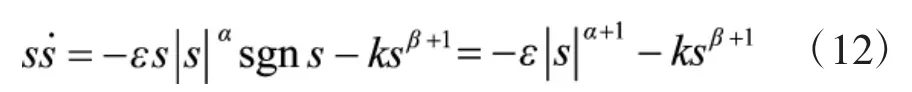
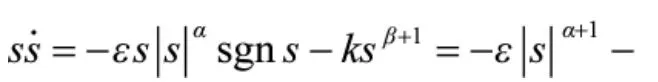
3　滑模控制律求取

对于含有扰动的不确定性系统而言，不确定性和扰动是无法获知的，在求解控制律时，只能利用被控系统的标称系统进行控制器设计。

则系统式（1）的标称系统为

当系统状态到达滑模面时

s=0（14）

对式（2）和式（14）求导得

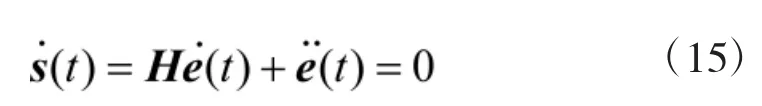
把式（13）代入式（15），并假设（CB）-1存在，整理得等价控制为

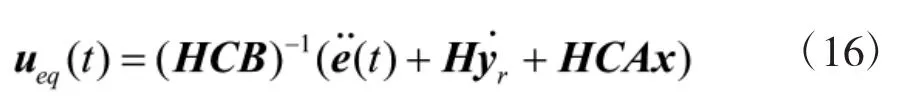
式（16）求取的控制律没有考虑实际系统中存在的不确定性和外部干扰等因素影响，也没有考虑系统趋近运动的品质。为此，本节采用u=ueq+△u的控制方案，其中ueq为等价控制，△u为切换控制。△u的作用是驱使系统状态或误差到达滑模面，并抵消系统参数摄动等不确定性和外部干扰的影响。

联立式（6）和式（13），求得控制律为

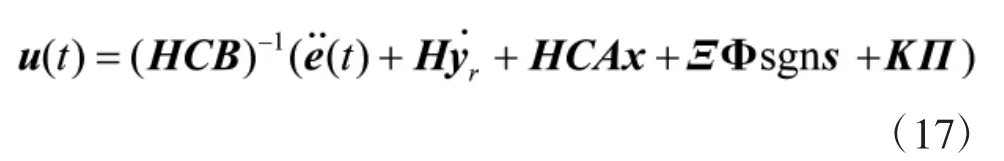
则由式（16）和式（17）知，

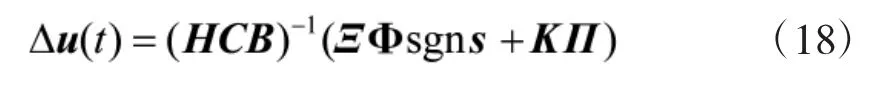
4　稳定性分析

设计控制器首先得考虑其稳定性，而后分析本节设计控制器的稳定性。

定义Lyapunov函数

对式（19）求导得

将式（6）代入到式（20）得

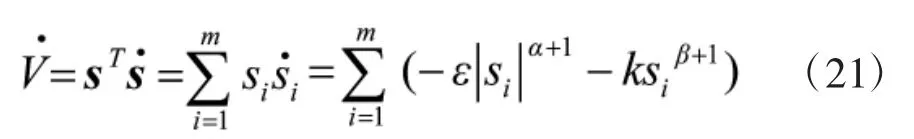
已知ε＞0，k＞0，1＞α≥0，β为正奇数，则

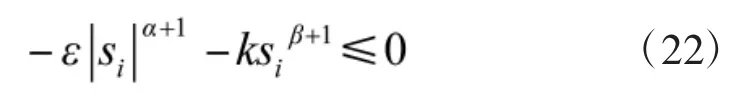
式（22）中的等于号只有在系统状态到达滑模面后才成立。

因此

由Lyapunov稳定性理论知，本文设计的控制器是稳定的。

5　仿真与结果分析

某型航空发动机在最大及其以上状态采用双变量控制计划，即用主供油量调节低压转子转速nL，喷管喉部面积调节涡轮落压比πL。以H=0 km，Ma=0为设计仿真点，其地面最大状态相对增量形式线性数学模型为：

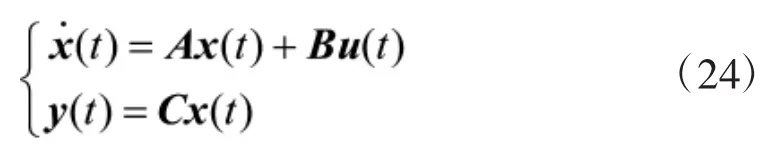
式中x=［nH，nL，mf，A8］T，u=［f8］T，y=［nL，πT］T；nL，nH，mf，A8，πT分别为发动机低压转子转速、高压转子转速、主供油量、尾喷管喉部面积和涡轮落压比。在实际系统中外部干扰等因素是不可避免的，为此设定f（k）值为

f（k）=［-0.2+0.25sin（0.015kπ），0.3+cos（0.03kπ），0，0］T。

设定参数H的初始值为［10，10］T，其值大小按照第①节设计的模糊规则输出变化，Ξ=diag ［1.2，1.2］，αi=0.5，i=1.2，K=diag［1.5，1.5］，βi=3，i=1.2。假设期望的输出向量yr=［1，1］T，初始状态向量x（0）= ［0，0］T。按照本文设计的控制器对低压转速nL和涡轮落压比πT进行阶跃响应仿真，仿真结果如图4和图5所示。

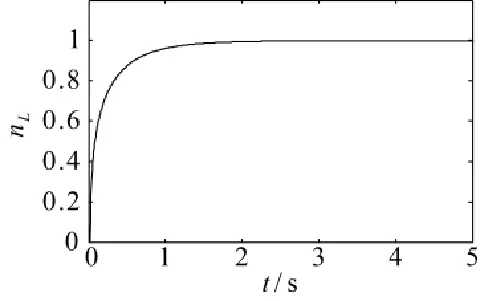
图4 H=0 km，Ma=0时低压转速nL阶跃响应曲线

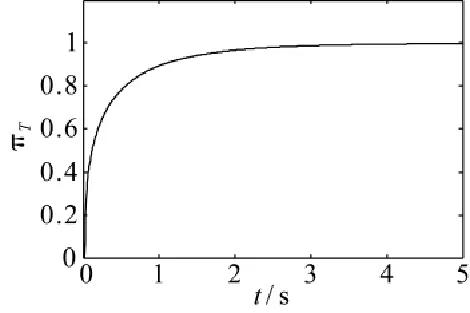
图5 H=0 km，Ma=0时涡轮落压比πT阶跃响应曲线

由图4和图5所知，本文设计的控制器响应快速，具有良好动态性能，削弱了抖振，无稳态误差。

在实际系统中，系统的参数摄动和外部干扰不可避免，尤其像航空发动机这种工作范围宽广的系统，在不同的工作状态，系统特性是不同的。为此，采用在地面状态（H=0 km，Ma=0）设计的滑模控制器，被控对象状态换为高空状态（H=10 km，Ma=1.0），此时航空发动机最大状态相对增量形式线性数学模型矩阵为：

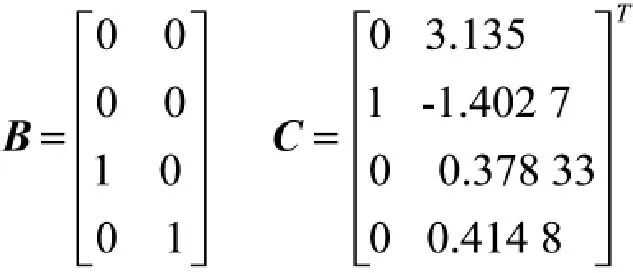
为此设定f（k）值为：

f（k）=［-0.2+0.25sin（0.015kπ），0.3+cos（0.03kπ），0，0］T。

同样，对低压转子转速nL和涡轮落压比πT进行阶跃响应仿真。仿真结果如图6和图7所示。可知虽然选取的仿真点偏离控制器设计点比较大，但系统输出响应还是比较快速，削弱了抖振。由于参数摄动和外部干扰的存在，使得低压转子转速和涡轮落压比都出现了不同程度的波动，但仍然满足发动机控制设计要求。分析原因是由于系统误差状态一开始还未到达滑模面，对参数摄动和干扰还不具有完全不变性，这也是本文采取模糊调节滑模面和改进幂指数趋近律缩短趋近运动时间原因所在。但随着系统误差状态到达滑模面，系统对干扰具有了不变性，最终系统到达指令位置，无稳态误差。

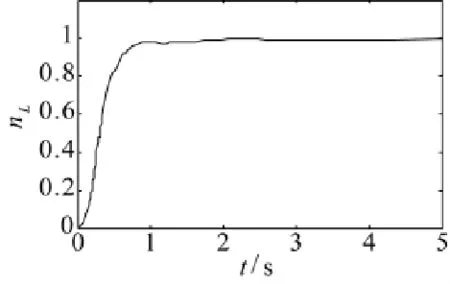
图6 H=10 km，Ma=1.0时低压转速nL阶跃响应曲线

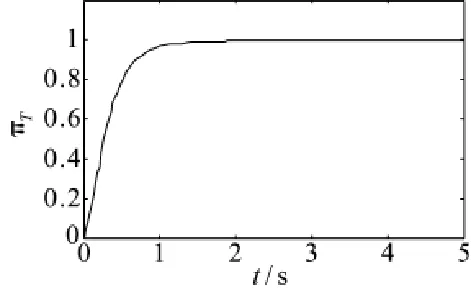
图7 H=10 km，Ma=1.0时涡轮落压比πT阶跃响应曲线

6　结论

本文针对航空发动机是一个具有不确定性的复杂系统，采用一种其参数模糊调节的时变滑模面，“主动迎上”系统状态轨迹，缩短趋近运动时间，提高控制器的鲁棒性。并且提出了一种基于改进幂指数趋近律的削抖控制方法，克服了传统指数趋近律的缺点并保留其优点，既加快了趋近速度又避免了抖振增加。仿真结果表明了该方法的有效性，削弱了抖振，对参数摄动和外部干扰具有一定的鲁棒性。将其作为航空发动机非线性控制器是完全可行、有效的。

参考文献：

［1］刘大响，程荣辉.世界航空动力技术的现状及发展动向［J］.北京航空航天大学学报，2002，28（5）：490- 496.

［2］张绍基.航空发动机控制系统的研发与展望［J］.航空动力学报，2004，19（3）：375-382.

［3］闫月亮，董照飞.航空发动机控制发展趋势及新技术浅析［J］.国际航空杂志，2006（7）：78-80.

［4］高为炳.变结构控制的理论及设计方法［M］.北京：科学出版社，1998.

［5］刘金琨.滑模变结构控制MATLAB仿真［M］.北京：清华大学出版社，2005.

［6］何秀然.航空发动机离散滑模变结构控制理论及应用研究［D］.西安：空军工程大学，2009.

［7］米文鹏，刘新学，洪成华，等.基于改进趋近律的模糊自适应滑导弹姿态控制系统［J］.导弹与航天运载技术，2009 （1）：15-19.

［8］KRUPP D，SHTESSEL Y B. Chattering-free sliding mode control with unmodeled dynamics［C］// Proc of American Control Conf，San Diego，IEEE Press，1999.

［9］HAJATIPOUR M，FARROKHI M. Chattering free with noise reduction in sliding-mode observers using frequency domain analysis［J］. Journal of Process Control，2010，20（7）：912-921.

［10］HO H F，WONG Y K，RAD A B. Adaptive fuzzy sliding mode control with chattering elimination for nonlinear SISO systems［J］. Simulation Modelling Practice and Theory，2009，17（8）：1199-1210.

［11］HUSSAIN M A，HO P Y. Adaptive sliding mode control with neural network based hybrid models［J］. Journal of Process Control，2004，14（1）：157-176.

［12］BARTOLINI G，PUNTA E. Chattering elimination with second-order sliding modes robust to coulom biriction［J］. Journal of Dynamici Systems，Measurement and Control，2000（122）：679-686.

［13］EDWARDS C. A practical method for the design of sliding mode controllers using linear matrix inequalities［J］. Automatica，2004，40（10）：1761-1769.

［14］YANG D Y，YAMANE Y，ZHANG X J. A new method for suppressing high-frequency chattering in sliding mode control system［C］// Proc of the 36th SICE Annual Conf，Tokyo，Japan，IEEE Press，1997.

［15］HACIOGLU Y，ARSLAN Y Z，YAGIZ N. MIMO fuzzy sliding mode controlled dual arm robot in load transportation［J］. Journal of the Franklin Institute，2011 （348）：1886-1902.

Fuzzy Sliding Mode Controller For Aeroengine Based on An Improved Power Exponential Reaching Law

TIAN Hu-sen1，XIE Shou-sheng1，MIAO Zhuo-guang1，2，WANG Lei1，3，Ren Li-tong1
（1. The Aeronautics and Astronautics Engineering Institute，Air Force Engineering University，Xi’an 710038，China；
2 .Unit 95961 of Chinese PLA，Beijing 100195，China；3. Unit 93704 of PLA，Beijing 101100，China）

Abstract：For the reaching process of sliding mode variable structure control without robustness，a method of fuzzy sliding mode controller for aeroengine based on an improved power exponential reaching law is put forward. The sliding mode surface adapted automatically by fuzzy system is proposed，which can shorten the time of reaching process to enhance the robustness by making the sliding mode surface near the system state. And an improved power exponential reaching law is designed，weakens the chattering. Simulation results show that the devised controller has good effect，effectively restrains the influence and weakens the chattering.

Key words：aero-engine，robustness，sliding mode variable structure control，reaching law，chattering

作者简介：田虎森（1989-），男，陕西汉中人，硕士。研究方向：飞机推进系统控制与监控。

收稿日期：2015-01-09

文章编号：1002-0640（2016）02-0108-05

中图分类号：V233.7

文献标识码：A

修回日期：2015-03-16