基于扩展比例导引律的制导模型*

张　刚，王运明

（1.江苏建筑职业技术学院，江苏　徐州　221116；2.南京理工大学自动化学院，南京　210094）



基于扩展比例导引律的制导模型*

张刚1，王运明2

（1.江苏建筑职业技术学院，江苏徐州221116；2.南京理工大学自动化学院，南京210094）

摘要：针对常用比例导弹导引律制导命中率低的问题，分析了比例导引律、偏置比例导引律、修正比例导引律的制导性能，提出了一种基于扩展比例导引律的制导模型，经仿真表明，该导引律具有目标垂直和水平机动跟踪能力，提升了反导作战的机动能力和效率。

关键词：制导模型，扩展比例制导，比例导引律，偏置比例导引律，修正比例导引律

0　引言

导引律是描述导弹质心运动的准则，用于确定弹道质心在空间的运动轨迹。在导弹的制导系统中，导引律的作用是确定导弹飞行并命中目标的运动学弹道。如何采用一种合适的导引方法来改善导弹的制导性能，提高导弹的命中精度是制导领域的热点问题。比例导引律具有易于工程实现、目标适应能力强等特点而被广泛应用于各类导弹上。

因此，本文详细分析了基本比例导引律、偏置比例导引律、修正比例导引律3种常用比例导引律的建模方法，并在3种比例导引律下对弹道轨迹和遭遇时间进行了仿真分析。在此基础上提出了一种基于扩展比例导引律的建模方法。该方法在对付大机动目标时可降低导弹的过载、脱靶量及命中时间，并提高了导弹的制导精度。

1　常用比例导引律建模方法分析

1.1比例导引律

比例导引律是自寻的导弹中采用最多的一种导引规律，具有对目标运动情况响应速度快，导引精度高、工程技术上易于实现等特点，因此，得到了广泛的应用。目前世界各国装备的自寻的式空空导弹大都采用传统的比例导引律，它具有导弹制导系统结构简单、对匀速目标射击时精度高和可靠性高等特点。

假定目标、导弹在同一个平面内运动，采用极坐标（r，q）来表示导弹和目标的相对位置，且导弹是一个可操纵质点，目标为运动质点。包括目标速度向量VT、导弹速度向量V，弹目之间相对位置如图1所示。其中，MT（弹目连线）称为目标瞄准线，q称为视角，r表示目标与导弹之间的相对距离。σT是弹道偏角（攻击平面为水平面），σ是弹道倾角（攻击平面为铅垂平面）；σT、σ是目标速度向量、导弹速度向量与基准线之间的夹角。

图中目标线旋转角速度dq/dt与导弹速度向量、目标速度向量关系式：

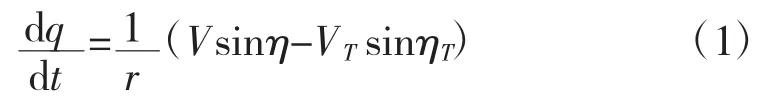
相对运动方程为：

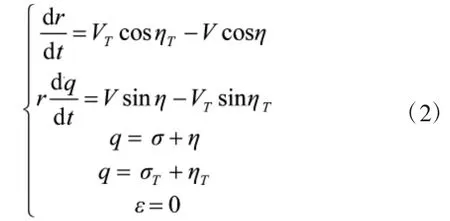
1.2偏置比例导引律

偏置比例导引律是指在比例导引律的原则上对比例导引视线角速度增加一个偏置量，然后在进行比例导引，表达式如下：

得出比例导引法关系式为

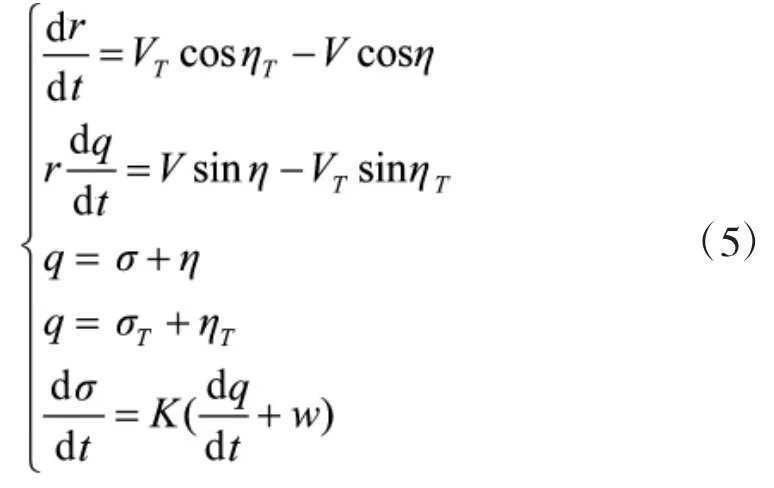
1.3修正比例导引律

为了避免在比例导引律中对付机动目标的视线角速度存在着发散导致目标的机动性能下降的问题，将比例导引律和追踪导引律结合起来，追踪法作为新导引律的修正项，得到一种新的导引律：

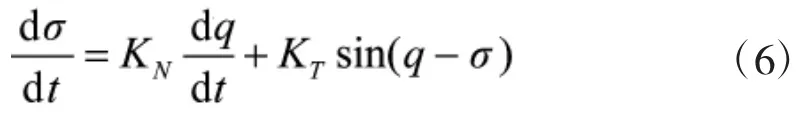
式中，等式右端的第1项为比例导引法，第2项为修正项。

1.4 3种比例导引律模型仿真分析

在制导系统初步设计阶段，为简化问题，突出重点，通常采用相对运动模型来研究导引弹道。

图2所示的比例导引示意图描述了导弹目标之间的相对运动模型，其中，Mk为第k个时刻导弹所处的空间位置，Mk+1为第k+1时刻导弹所在的空间位置。Tk为第k个时刻目标所处的空间位置，Tk+1为第k+1时刻目标所在的空间位置。r（k）表示第k个时刻导弹和目标之间的距离。Sm表示一个时间间隔内导弹运动的距离，Sm=vm×△t。xm，ym，zm表示导弹的立体直角纵坐标，xt，yt，zt表示目标的立体直角纵坐标。仿真弹道时，采用差分方法，求每隔一段时间的导弹离散三维离散坐标，以此绘制出理想弹道，并仿真得出导弹目标遭遇时间。

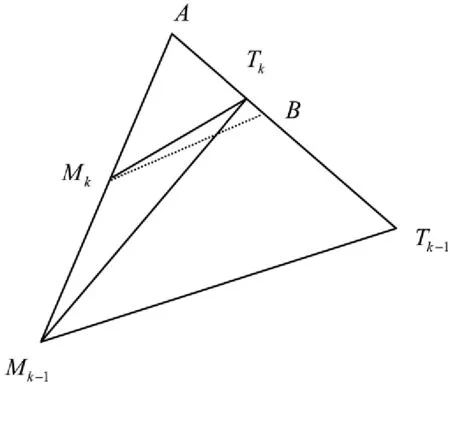
图2比例导引示意图

在导引系数k=3，偏置量和修正项的值为0.002时，对前面阐述的比例导引律、修正比例导引律、偏置比例导引律进行仿真分析，得到的弹道轨迹曲线如图3所示。从上至下依次为修正比例导引律曲线、偏置比例导引律曲线、比例导引律曲线、目标曲线。遭遇时间如图5所示，得出表1所示。

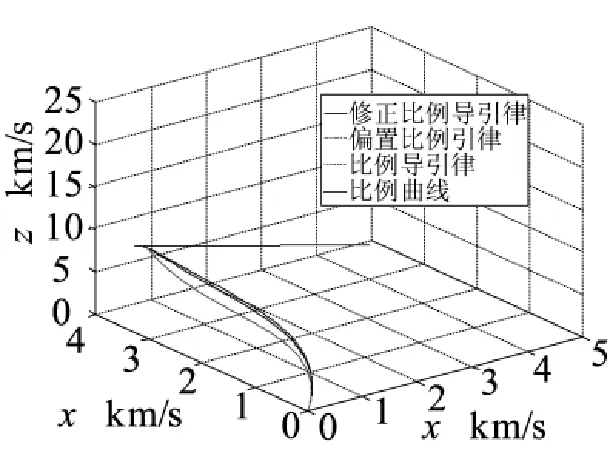
图3 3种比例导引下的弹道轨迹图

表1遭遇时间表

仿真结果分析：

（1）ω=0.002时，k取值范围为1～6，步长为0.5，通过多次仿真分析比较3种比例导引法的遭遇时间，得到遭遇时间曲线图4所示。通过仿真表明，当ω固定时，随着导引系数的增大，遭遇时间逐渐减小到一定值后趋于稳定。在参数ω=0.002、k取1～6下，偏置比例导引优于其他两种导引律，修正比例导引次之。在k取值为5.5~6.0时修正比例和偏置比例的弹目遭遇时间最短为19.7 s，均优于纯正比例导引律。

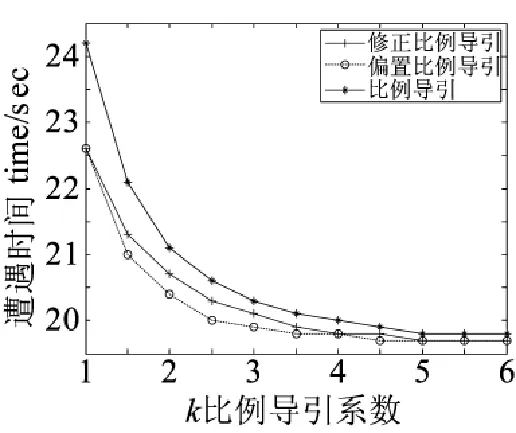
图4不同比例导引系数下遭遇时间图

（2）在k=3、ω=0.002，导弹的速度取500 m/s～850 m/s时，通过多次仿真分析比较3种比例导引法的遭遇时间，得到遭遇时间曲线图5所示，通过仿真表明，随着导弹的速度的增大，3种比例导引下的弹目遭遇时间逐渐减小趋于平缓。

图5不同导弹速度下遭遇时间图

2　扩展比例导引律模型

现代拦截目标正向着高速和高机动性方向发展，这给导引律设计提出了更高要求。为此，人们一直在不断地改进比例导引律，期望能进一步有效地克服目标大机动等不确定因素对导引性能的影响。比例导引律在导弹拦截非机动目标时存在零脱靶量，脱靶量表示导弹和目标的距离，当目标作较大机动时，比例导引律脱靶量较大，不能满足拦截大机动目标的要求。因此，本文提出了一种扩展比例导引律，根据不同的导弹和目标的参数值选取合适的导引系数和偏置修正参数来减少比例导引律的脱靶量。导引方程为：

其中，k为导引系数，ω为偏置修正参数。

针对不同的参数选择，设置参数k、ω的值。当k 为1时，等同于偏置比例导引；当ω为零时，等同于传统比例导引。

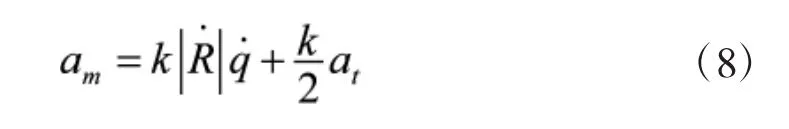
其中k为比例系数，一般取值3~5，am为导弹指令加速度，为弹目接近速度，at为目标加速度在垂直视线方向上的分量为视线角速度。

扩展比例导引制导规律在经典比例导引上对导弹的加速度、重力的影响及目标机动的影响进行补偿，经补偿后，导弹接近目标时，弹道平直，需用过载趋近于零，从而减小脱靶量。系统一般采用比例制导，当出现较大脱靶量时，采用扩展比例导引。ω根据实际情况进行补偿。通过仿真验证，改进的导引律在对付大机动目标时可降低导弹的过载、脱靶量及命中时间，极大地提高了导弹的制导精度。

经过研究分析，结合复合制导的思想，在导弹处于初始段，速度较大；当导弹到达一定的位置，速度趋于平缓。于是假设选取k为3，ω为速度的分段函数，与之前的修正比例导引律、偏置比例导引律、比例导引律进行仿真比较分析，假设目标初始位置位于（4，3，4），导弹对其进行攻击。为了便于观察，假设目标速度大小为0.42 km/s，导弹在攻击其中速度变化不大，近似为0.6 km/s，时间间隔为0.1 s，当导弹与目标之间的距离＜60 m，就认为遭遇。在导引系数

k=3，偏置量和修正项的值为0.002时，得到如图6所示的三维轨迹图。

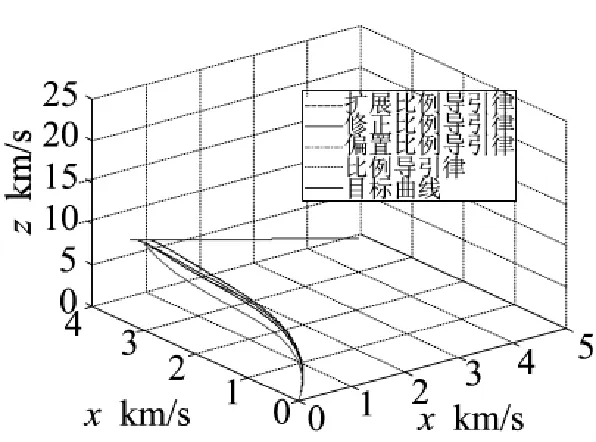
图6仿真比较图

通过仿真表明，采用扩展比例导引律的遭遇时间为19.1 s，均小于其他比例导引律的遭遇时间，表明该导引律具有较强机动性，能够快速打击目标。

4　结论

比例导引律经过长期的发展，在基础理论、实际应用中都取得了长足的发展，尤其是其改进形式更是得到了广泛应用。为了满足高技术条件下的战争需求，应以现有的实用制导规律为基础，扬长避短，同时结合实际需要，利用最新的相关学科知识与技术，对其作进一步的改进研究和优化设计。

参考文献：

［1］郭广明，方群.变论域策略在导弹模糊制导律设计中的应用［J］.火力与指挥控制，2011，36（5）：177-181.

［2］肖增博，雷虎民，滕江川，等.多导弹协同制导规律研究现状及展望［J］.航空兵器.2011，12（6）：18-23.

［3］葛连正，沈毅，院老虎.前向拦截的三维制导模型及制导律设计［J］.系统工程与电子技术，2008，30（6）：1118-1121.

［4］肖增博，雷虎民，宋龙，等.基于自抗扰控制的导弹三维制导规律［J］.固体火箭技术，2011，34（5）：548-563.

［5］胡诗国，方洋旺，张平，等.一种近空间高超声速飞行器的制导律设计与仿真［J］.弹道学报，2011，23（3）：7-12.

［6］XIAN Y，SI W H. Research on midcourse maneuvering penetration guidance law of ballistic missile based on genetic algorithm［M］. IEEE，2009.

［7］HAN Y H，XU B. Variable structure guidance law for attacking surface maneuver targets［J］. Journal of Systems Engineering and Electronics，2008，19（2）：337-341.

The Research of Guidance Model Based on the Extended Proportional Guidance Law

ZHANG Gang1，WANG Yun-ming2
（1. Jiangsu Institute of Architectural Technology，Xuzhou 221116，China；
2. School of Automatic，Nanjing University of Science and Technology，Nanjing 210094，China）

Abstract：For the low percentage of missile guidance law，it analyzes guidance performance of proportional guidance law，a bias proportional guidance law and the guidance law modified proportional，a new patulous proportional guidance model is proposed，after particular analysis，this guidance law with vertical and horizontal maneuvering target tracking capability，enhance the anti missile combat maneuver capability and efficiency.

Key words：guidance mode，patulous proportional guidance，proportional guidance law，bias proportional guidance law，modified proportional guidance law

作者简介：张刚（1986-），男，江苏徐州人，硕士。研究方向：计算机仿真。

*基金项目：国家“863”计划基金（2010XX）；辽宁省教育厅创新团队基金资助项目（2008403002）

收稿日期：2015-01-05

文章编号：1002-0640（2016）02-0082-03

中图分类号：TJ39

文献标识码：A

修回日期：2015-03-12