分布式麦克风阵列的声源定位*

张会新，闫安斌，王　昕，姜　维

（1.中北大学电子测试技术国家重点实验室，太原　030051；2.仪器科学与动态测试教育部重点实验室，太原　030051；3.北京宇航系统工程研究所，北京　100076）



分布式麦克风阵列的声源定位*

张会新1，2，闫安斌1，2，王昕3，姜维3

（1.中北大学电子测试技术国家重点实验室，太原030051；2.仪器科学与动态测试教育部重点实验室，太原030051；3.北京宇航系统工程研究所，北京100076）

摘要：声定位探测技术的无源被动特性，使其在定位技术研究领域内独树一帜，时延估计和定位算法是支持这一技术的核心。DUET时延估计算法简单，通过对接收到的信息分段帧移加窗处理，能够有效识别有用语音信息，时延估计精度较高，在高噪声的环境中非常适用；球面定位算法是基于时延估计提出的，对麦克风的排列形式不固定，适用于任意排布的麦克风阵列，并且在时延估计精度较高的情况下，能够很准确地对声源目标进行定位。

关键词：声定位，DUET，时延估计，帧移加窗处理，球面定位算法

0　引言

麦克风阵列的声源定位属于被动声测技术，它是利用物体运动或振动时产生的音频信号，通过对该音频信号进行采集、提取和分析，实现对发声体定位的一种技术。麦克风阵列是指若干个具有相同性能或性能接近的麦克风群体，它们有的被以某种规则的几何形式进行排列，有的则是随机地散布在某些应用区域中。

阵列的选取对目标定位的精度影响很大［1］，常见的阵列形式有直线型和十字型。均匀线阵结构简单，计算量小，但其获得信息量也较少，只适用于平面定位；十字阵列由相互垂直的线阵组成，中间阵元共用，较线性阵列结构复杂，所获得的信息量也较多，通过适当的计算，这些信息量可以测算出声源的俯仰角、方位角及距离；但规则的阵元排布需要人为去实现，不适用于传感器节点的大量散布和空投方式，也不利于将节点散布在有争议或人类不适宜到达的区域，故本文提出一种基于任意阵列的定位算法，任意阵排布的麦克风阵列结构复杂多样化，实际应用比较简单，其缺点是计算量相对较大。

1　时延估计

在声阵列定位系统中，精确测量声源目标的相对距离和相对方位参数的关键，是要能够准确而又及时地得到声源发出的音频信号到达接收麦克风质检的时延值，时延估计技术显得尤为重要。传统的时延估计算法是通过计算信号与信号之间的相关性，根据相关函数得到时延差。这种算法对只存在单一声源的场合中，计算简单，时延估计比较准确，但在实际情形中，往往不可能只存在唯一的声源，这将导致传统时延估计采用的互相关法，因噪声的存在，使得信号之间的时延旁瓣过高，而无法准确得到目标声源到达不同麦克风的时延。目前出现的一类基于时频稀疏特性的算法，该算法实现简单，能同时对多个声源信号进行分离。尤其Van Hulle提出的DUET算法应用最为广泛［2］。

1.1语音信号的加窗处理

语音信号的频率随时间的变化而不同，几乎没有完全重合的两段声音谱线，但在众多学者的长期试验与探索中，发现在一段很小的时间内，语音信号的频率基本是平稳的。故对语音信号的分析，需将信号进行分段后才能进行后续的处理。一般为了保持信号的连续性，使得帧与帧之间平滑过渡，通常采用交叠分段的方法［3］，前后帧的交叠部分称为“帧移”，如图1所示。

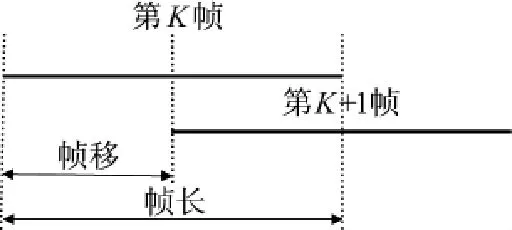
图1帧移与帧长关系图

语音信号的分帧是利用可移动的有限长度窗口进行加权来实现的。即利用窗函数w（n）与信号s（n）相乘，常用的窗函数有两种，一种是矩形窗，另一种是汉明窗。窗函数的选择直接影响语音信号的短时分析特性（语音信号的特性变化），进而影响到后续的延时处理，直接导致定位的精度。

窗函数的选择主要考虑两个方面：窗口形状和窗口长度。从形状上看，汉明窗的主瓣宽度是矩形窗的两倍，同时带宽增加了一倍，带外衰减也是矩形窗的两倍，故汉明窗较矩形更能够保证波形成分的完整［2］，窗口长度的确定由采样频率和频率分辨率共同决定：

从表达式不难看出，当采样频率确定后，窗口长度取长，则频率的分辨率便会降低；若提高频率分辨率，则会使窗口的长度变短，两者变化相互矛盾。换言之，窗口长度如果取长，则不能如实反映语音信号幅度变化，反之，则短时能量将随时间产生很大变化，使得能量函数不够平滑。

根据实际需求，当采样率在20 KHz时，窗口长度N通常取200点~600点即可（即10 ms ~30 ms的短帧时间）。

1.2 DUET时延估计算法

语音信号是时频稀疏和短时正交的，即每个声源发出的声音在频率上都只集中在一个比例很小的范围内，并且各个声源发出声音的频率分布几乎互不交叠［4］。换言之，假设两个语音信号源si（t）和sj（t）经过一个矩形窗的窗函数W（t）傅里叶变换后，在频域上是互不交叠的，即认为两语音信号si（t）和sj（t）短时正交。

在无反射无混响的情况下，假设阵列中的两个同质麦克风收到来自多个语音源信号s1（t），s2（t），…，sn（t）组成的混合信号，则两路麦克风收到的信号可以表示为：

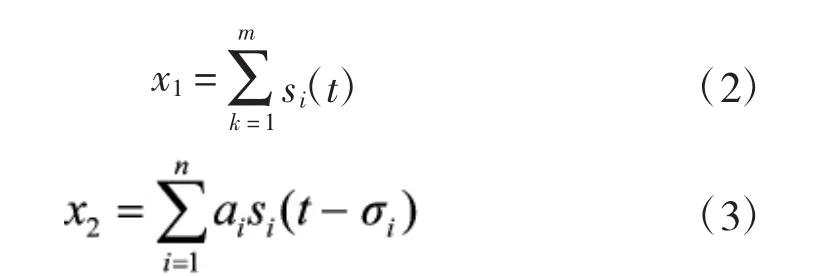
其中，x1表示麦克风1接收到的混合信号，x2表示麦克风2接收到的混合信号，δi表示两麦克风之间的相对延时，ai表示语音信号到达两麦克风之间的相对衰减系数。

基于无反射无混响的假设前提，对两路信号进行加窗傅里叶变换，将信号的时域表达式转换为频域表达式：

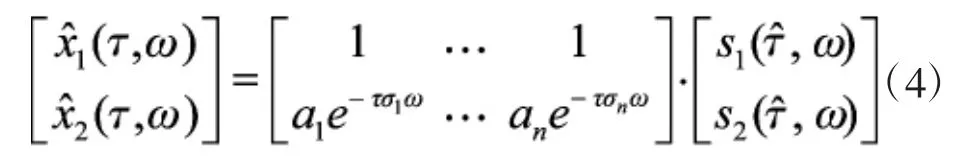
由于语音信号满足时频稀疏和短时正交性，故可以认为在每一个时频点（τ，ω）处，最多只有一个声源起主导作用，则每个时频点处的频域表达式可以表示为：

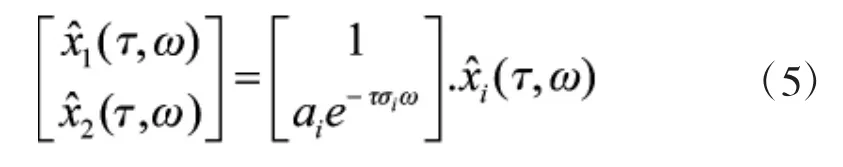
其中，x赞i（τ，ω）指在时频点（τ，ω）处起主导作用的声源信号的傅里叶变换。

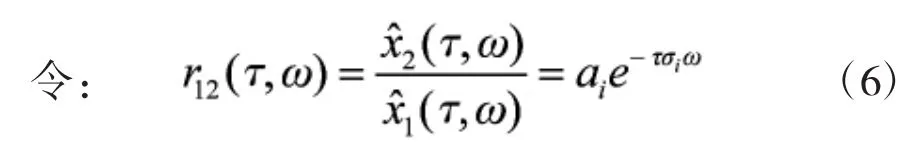
扩展到N个同质麦克风，则可得到任意两个同质麦克风在时频点（τ，ω）处的频域相关系数矩阵：

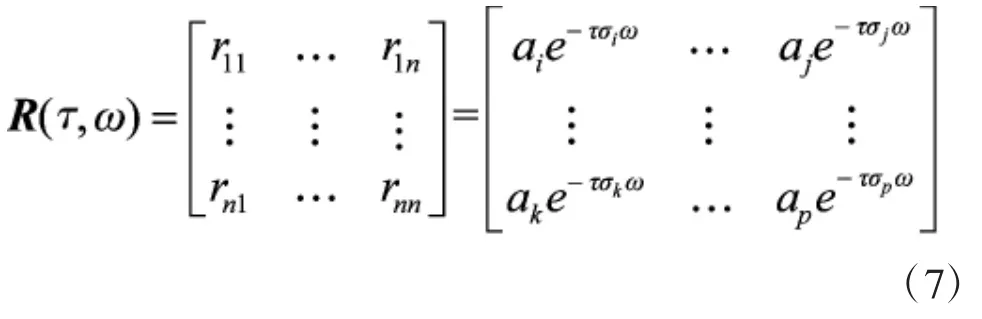
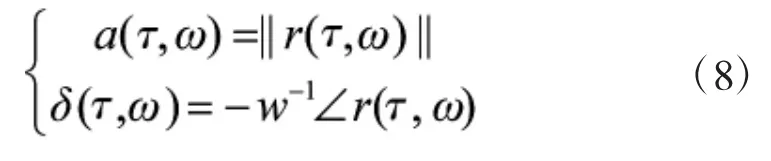
由于本文使用的定位计算是通过得到信号源产生的信号到达各个麦克风的时间差，确定声源距离两麦克风的距离差，进而得到声源的位置，故在此暂不考虑a（τ，ω）。

最后确定声源对应于各个麦克风的时延参数δ（τ，ω），是通过对得到的所有参数进行加权聚类处理，对于移动速度比较慢或者静止的声源，短时内，信号到达两麦克风的时延是固定的，故经计算得到的时延参数会散落在各自实际时延值的附近，根据概率估计便可估计出实际的时延值。

2　阵列定位算法

任意排布的麦克风阵列，由于其摆放形式比较自由，投放形式也比较自由，更加适用于有争议的地区或者人无法直接到达的区域，实用性更强。

2.1时延定位算法（TDOA）

时延定位（TDOA）算法是通过研究和探测声波的传播情况来对目标进行定位的。声音在同种介质中传播的速度是一定的，由于其传播速度相对于光速和无线电传输速度比较小，声源发出语音信号与麦克风接收该语音信号之间会存在一定的时延，并且该时延相对较大，利用音信信号到达每个接收麦克风的时延都不同，提出了基于时延的定位算法。

根据时延定位算法理论，构建的数学模型如式

化简可得：

（9）所示：

其中，ti为声源发出语音信号与麦克风接收该语音信号的时延，ri表示语音信号接收麦克风距离声源的距离，ni表示由于测量误差引起的随机噪声。同理，可以推广到麦克风阵列中其他麦克风对应的时延数学模型：

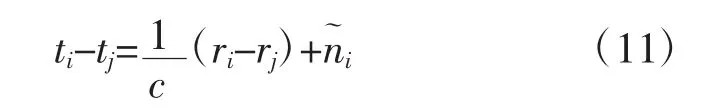
由此，只要计算出传感器节点之间的相对时延，即可清楚地定位被测目标声源的位置。

2.2球面交汇法［5-6］

设阵列阵元按任意位置摆放，如图2所示，将阵元O置于原点作为参考点（x0，y0，z0），

通过等式变焕，可以得到：

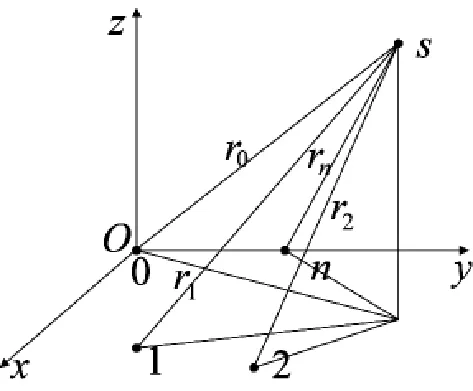
图2球面交汇法示意图

阵列中其他第i个麦克风节点的坐标设为（xi，yi，zi），声源S的坐标用（x，y，z）表示，ri表示声源S与第i个麦克风的距离。结合上图并根据时延定位算法思想，可得到其定位的数学模型：

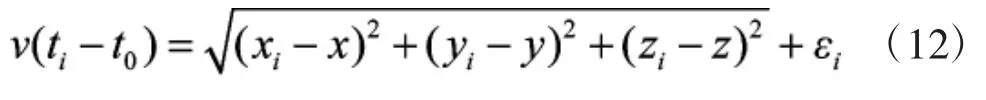
或

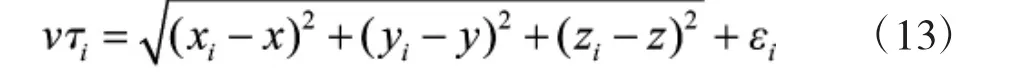
其中，t0表示声源S开始发射信号的时刻，ti为第i个麦克风接收到信号的时刻，εi为模型测量误差，τi=ti-t0。

比如，当阵元的个数是3的时候，得到的方程组如式（14）：

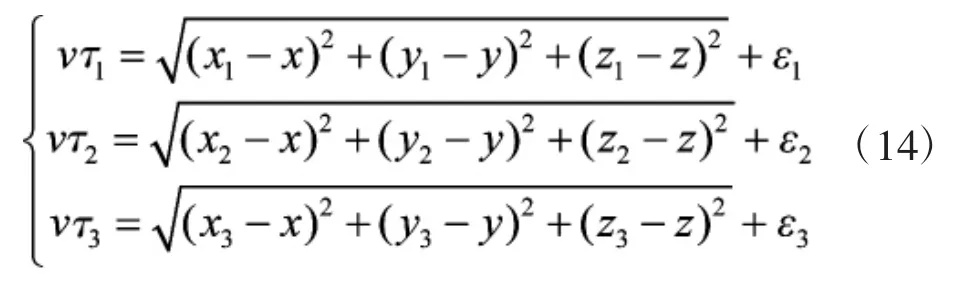
令

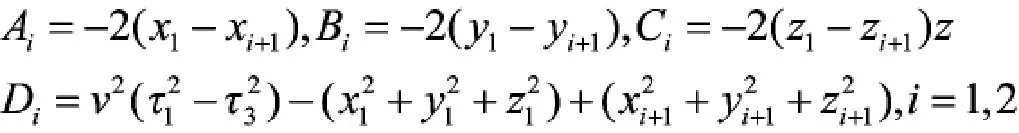
则，式（14）可转换为：

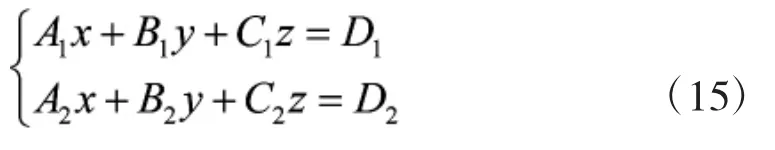
由上述方程可得：

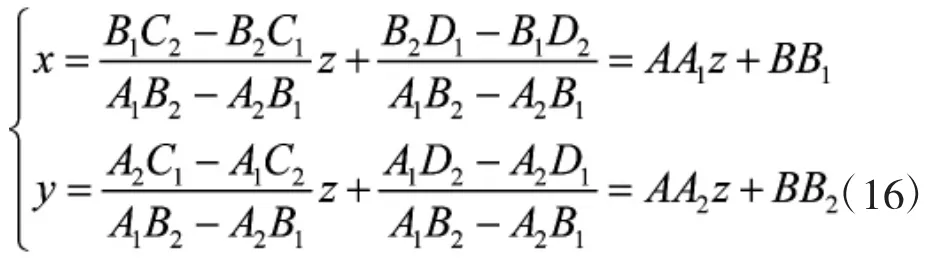
又由式（14）和式（16）可得

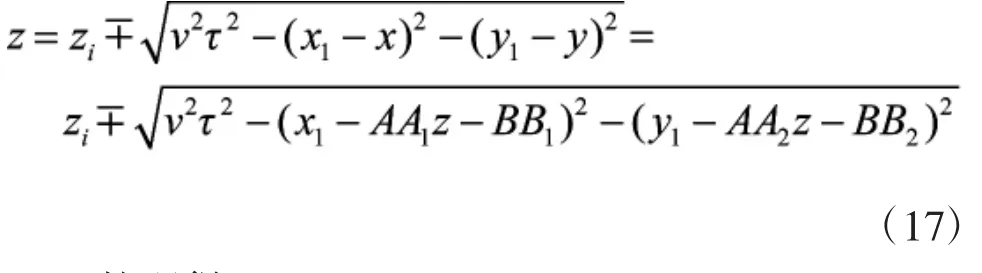
整理得：

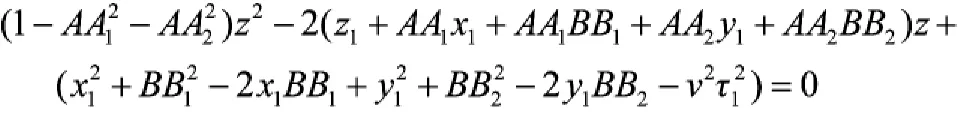
即

az2+bz+c=0

解得：

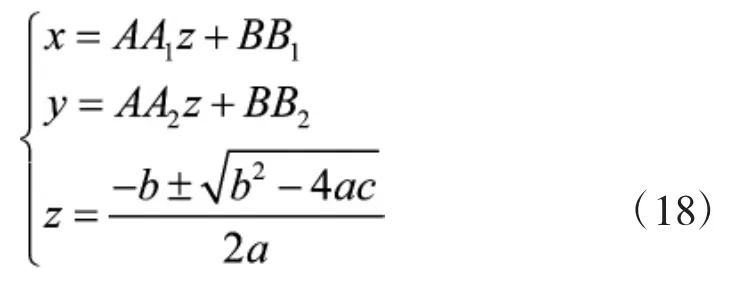
由上述推导可知，此模型至少需要3个麦克风即可计算出声源坐标（x，y，z）的值（当多余3个时，可使用最小二乘法计算最佳解）。

3　仿真分析

为了验证该算法的有效性，本节基于模拟仿真软件，做了大量的试验，并对试验结果进行了深入的理论分析。通过研究分析表明，DUET时延算法对有干扰源的声源环境中，能有效识别有效信息，并能够有效得到不同麦克风接收声源信息之间的时延值，对后续的定位算法起关键作用。球面交汇法适用于任意排布的麦克风阵列的声源定位，定位的相对误差较小，能够有效地对声源位置进行定位。3.1 DUET时延算法仿真分析

本次时延仿真试验中，设定声源距离麦克风a 为40 m，距离麦克风b为50 m，a、b两麦克风距离为20 m，采样频率为20 KHz，阵列采样的信号长度为2.1 s，为兼顾语音信号的短时平稳特性，本次设定信号帧长为30 ms，帧移为1/2。根据DUET算法，对每帧数据汉明加窗后进行1 024点的短时傅里叶变换，得到麦克风接收到的混合信号的模型，构建阵列麦克风频域矩阵，对矩阵进行相关性计算，得到相关系数矩阵，进而得到各个麦克风之间的时延。

利用大数定理，对得到的时延样本进行估计，以确定最终的时延值。图3为本次仿真试验结果图：

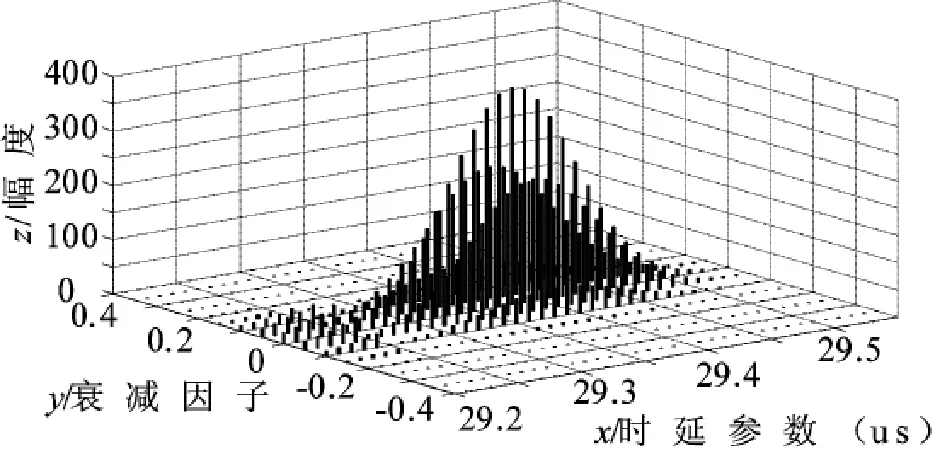
图3时延估计样本分布三维图

由图3可以看出，中间出现一个尖峰，尖峰对应的时延值大概为29.38 ms，基本接近实际时延值29.41 ms，故此算法对有噪声干扰的环境中的声源信号时延估计具有适用性。

3.2球型定位算法仿真分析

构建三维立体坐标系，假设3个麦克风的坐标分别为a（0，0，0，），b（3，8，0），c（11，4，0），声源S坐标为（19，6，10），如图4所示：

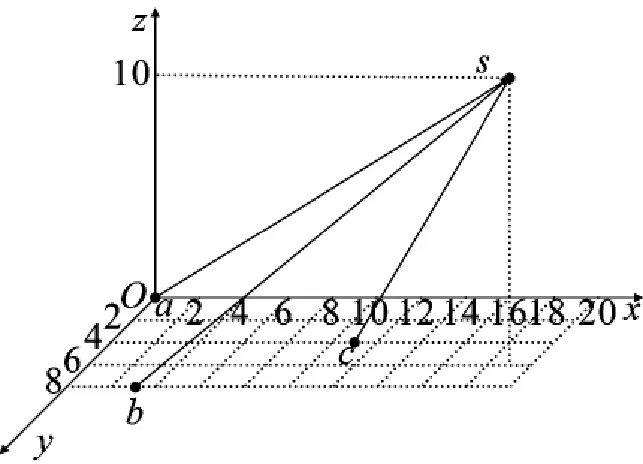
图4声源与麦克风位置示意图

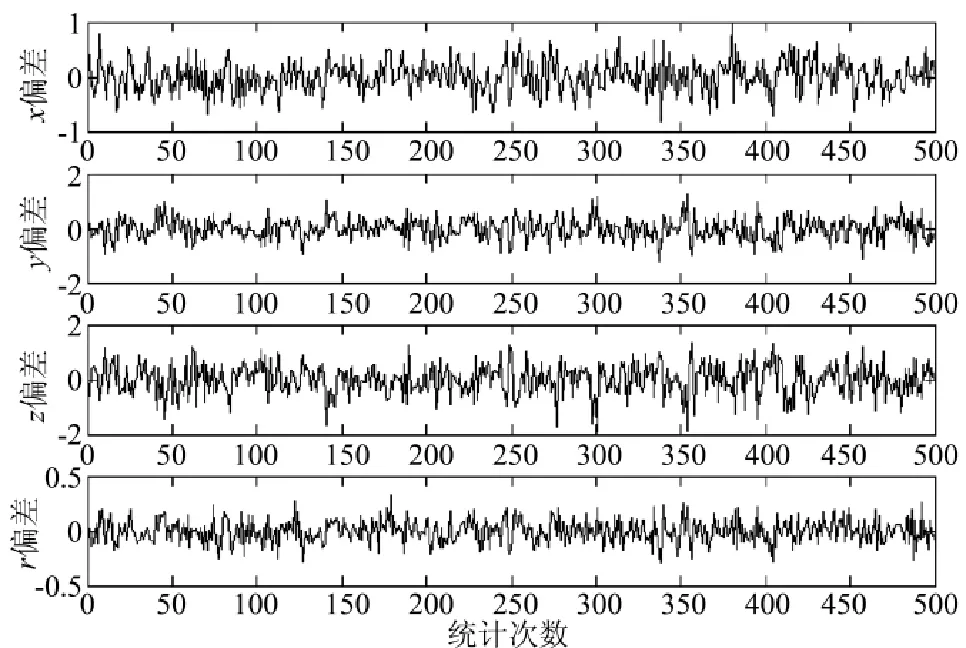
图5球面交汇法定位计算误差统计示意图

当时间测量误差呈50 us的正态分布时，用球面交汇定位法对声源的3个坐标系进行偏差计算及距离的偏差计算，统计结果如图5所示，本次仿真试验共统计500次。

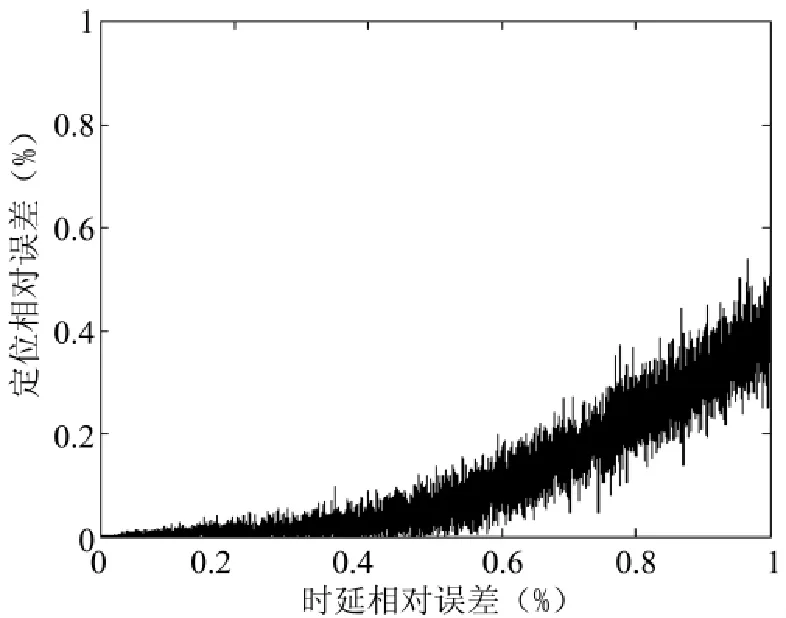
图6球面定位误差与时延误差的关系示意图

此外，图6给出了时延误差对球面交汇法声源定位的影响的示意图。

从图6可知，当时延相对误差控制到0.4以下时，可将定位的相对误差控制到0.1以下。

4　结论

声定位探测技术因其无源被动的特性，已成为目前定位技术研究的一个重要方面。时延估计和定位算法的选择都是决定定位精度的关键技术。本文提到的DUET时延估计算法，适用于噪声比较复杂的环境中，并且时延估计精度较高；球面定位算法在时延估计误差较小的情况下，其定位精度也相对较好。

参考文献：

［1］HE J，LIU Z. Two-step azimuth and elevation angle estimation with vector hydrophone array［J］. Chinese Journal of Electronics，2009，18（4）：754-758.

［2］顾添翼.基于麦克风阵列的多声源侧向方法研究［D］.南京：南京理工大学，2014.

［3］甘海波.语音识别系统中声学层模型的研究［D］.哈尔滨工业大学，2008.

［4］ARBERET S，GRIBONVAL R，BIMBOT F.A robust method to count and locate audio sources in a multichannel underdetermined mixture［J］. Signal Process，IEEE Transaction on，2010，58（1）：121-133.

［5］王鹏.基于MEMS矢量水听器阵列的声目标定向定位技术研究［D］.太原：中北大学，2013.

［6］雷鸣，陈绍钦，雷志勇.近地炸点声定位算法研究［C］.计算机测量与控制，2012，20（3）：734-736.

Sound Source Localization Distributed Microphone Array

ZHANG Hui-xin1，2，YAN An-bin1，2，WANG Xin3，JIANG Wei3
（1. National Key Laboratory for Electronic Measurement Technology，North University of China，Taiyuan 030051；2. Key Laboratory of Instrumentation Science & Dynamic Measurement of Ministry of Education，Taiyuan 030051，China；3. Beijing Institute of Astronautics System Engineering，Beijing 100076，China）

Abstract：Passive features of Acoustic positioning detection technology make it unique in the field of positioning technology，TDE and positioning algorithm is the core to support this technology. DUET delay estimation algorithm is simple，with segmenting information received via the docking frame shift windowing，it can effectively identify useful speech information，high delay estimation accuracy is corporately accurate which is suited in high -noise environments ideally；spherical delay estimation algorithm is put forward based on TDE，the arrangement of the microphone is not fixed in the form of its requirements，and therefore is applicable to any arrangement of the microphone array，and in the case of high precision delay estimation，it can accurately position the sound source target.

Key words：acoustic positioning，DUET，TDE，windowing frame shift，spherical localization algorithm

作者简介：张会新（1980-），男，山西太原人，讲师。研究方向：动态测试技术及智能仪表。

*基金项目：国家“863”计划基金资助项目（2011AA0404040）

收稿日期：2015-01-12

文章编号：1002-0640（2016）02-0077-05

中图分类号：TN925+.1

文献标识码：A

修回日期：2015-03-07