基于联系数的电子装备体系效能倍增效应分析*

夏　斌，徐　勇，柯宏发，贺齐辉

（1.中国洛阳电子装备试验中心，河南　洛阳　471003；2.总装备部工程设计研究总院，北京　100028；3.装备学院复杂电子系统仿真重点实验室，北京　101416）



基于联系数的电子装备体系效能倍增效应分析*

夏斌1，徐勇2，柯宏发3，贺齐辉1

（1.中国洛阳电子装备试验中心，河南洛阳471003；2.总装备部工程设计研究总院，北京100028；3.装备学院复杂电子系统仿真重点实验室，北京101416）

摘要：提出了基于联系数的电子装备系统和体系作战效能倍增效应分析新方法。首先介绍了联系数的定义与数学运算，其次提出以基于作战能力指数的同异联系数来描述电子装备的作战效能，并根据不确定系数的取值分别对电子装备系统和体系的作战效能倍增效应进行了分析，最后基于侦察装备对目标的侦察能力进行了实例分析，结果表明该方法合理可行。

关键词：系统工程方法论，作战效能，倍增效应，联系数，电子装备体系

0　引言

文献［1］中把比较复杂的研究对象称为系统，即相互作用和相互依赖的若干组成部分组合而成的具有特定功能的有机整体。这个系统又从属于一个更大的系统。而体系则定义为系统之系统［2-8］。系统要素的功能必须服从系统的整体功能，系统的功能不等于要素功能的简单相加，各种武器组成系统或体系后就可能会产生“兵力倍增器”［9］的作用。从对这些文献的分析来看，虽然体系对作战效能的提升作用基本上只是以语言或定性地分析，并指出分析过程中存在的不确定性问题，很少的文献能进行定量的分析；但是可以肯定，目前基于随机、模糊等信息机理的不确定性分析方法是对体系作战效能倍增效应进行分析的公认的可行方法。集对分析法（Set Pair Analysis，SPA）是我国学者赵克勤提出的一种新的系统分析方法［10-11］，本文提出利用基于作战能力指数的同异联系数来描述电子装备的作战效能，并根据不确定系数的取值分别对电子装备系统和电子装备体系作战效能的倍增效应进行了分析。

1　联系数的定义及运算

1.1联系数的定义

集对分析实质上是一种新的不确定性理论，其核心思想是将确定、不确定视为一个确定、不确定系统；它是从同、异、反三方面研究两个事物的不确定性关系，全面刻画二者之间的联系。在这个系统中，确定性和不确定性相互联系、相互影响、相互制约，并在一定条件下相互转化，概念联系数充分体现了上述辩证思想，能够统一描述模糊、随机、中介和信息不完全等所致的各种不确定性，从而把对不确定性的辨证认识转化为具体的数学运算。将具有某种一定联系的两个集合A和B组成的对子，记为H（A，B），对组成集对的两个集合特性作同一性、差异性、对立性分析，其特性用联系数进行定量刻画，有两个集合的联系数表达式

式中N为集合特性的总数，S为同一特性的个数，F为差异特性的个数，P为对立特性的个数；i为差异不确定系数，在［-1，1］之间视不同情况取值，有时仅起差异标记作用；j为对立度系数，在计算中j=-1，有时仅起对立标记作用。为简便计，称a=S/N为同一度，b=F/N为差异度，c=P/N为对立度，其中a、b、c为非负且满足归一化条件a+b+c=1。上述联系数表达式可写为

μA-B=a+bi+cj（2）

式中a、b、c为非负，但不要求满足归一化条件时，上述联系数称为同异反联系数或三元联系数，有时根据实际需要进一步将三元联系数或同异反联系数表达式简化为如下的二元联系数表达式：

μA-B=a+bi（3）

μA-B=bi+cj（4）

μA-B=a+cj（5）

上面3个表达式分别称为同异联系数、异反联系数、同反联系数表达式。

联系数μA-B具有宏观、微观两个层次，联系数中的a和c分别是对事物同一和对立两种状态的定量刻画，同时又可以对介于同一和对立之间的不确定性进行区分，宏观层次上的不确定性用b来度量，微观层次上的不确定性用不确定系数i来承载。i并不是在联系数的确立过程中确定的，而是在3个宏观参数确定后赋予b，目的在于进一步在微观层面上对不确定性程度进行调整。联系数μA-B具备了从宏观和微观两个尺度对系统进行刻画的能力。

1.2联系数的运算

设有3个联系数u1=a1+b1i、u2=a2+b2i和u3=a3+b3i，则有

①加法运算

u1+u2=a1+b1i+a2+b2i=（a1+a2）+（b1+b2）i（6）

由运算规则可知，联系数满足加法交换律与结合律，且可推广到有限个联系数的和。由加法运算规则还可以推导出平均联系数表达式：

②减法运算

u1-u2=a1+b1i-（a2+b2i）=（a1-a2）+（b1-b2）i（8）

③乘法运算

u1·u2=（a1+b1i）×（a2+b2i）=a1·a2+（a2b1+a1b2+b1b2）i（9）

④除法运算

⑤关系运算

联系数u1与u2相等，联系数的同部和异部必须分别相等，即

u1=u2圳a1=a2，b1=b2（11）

联系数u1与u2在比较大小时，与i的取值有关。当i∈［-1，1］时，若u1-u2＞0，则有u1＞u2；若u1-u2＜0，则有u1＜u2。

2　电子装备系统和体系

体系的基本含义是指“系统的系统”，电子装备体系是指为了完成电子对抗作战任务，为发挥最佳整体作战效能，而由功能上相互联系、性能相互补充的各种电子装备系统按照一定结构综合集成的更高层次的电子装备系统。可见体系是一类特殊的系统，电子装备体系的基础是电子装备。

电子装备体系的作战效能是指在体系规模范围内，在给定的作战条件和作战环境中，完成作战使命和达到预期目标的能力。该体系中的任何一套电子装备系统所发挥的作战效能，除了该电子装备系统本身具备的作战效能外，还受到其他电子装备系统的影响、制约等作用，因此，难以基于加性或拟加性函数对各电子装备系统的作战效能进行简单的累加组合而得到体系的整体作战效能。另外，战场环境的时变性、各个电子装备系统之间的相关复杂性、以及各种函数关系数学模型描述的非精确性等不确定性，也使得电子装备体系作战效能的分析难度极大。

联系数对客观存在的种种不确定性予以客观承认，并把不确定性与确定性作为一个既确定又不确定的同异反系统进行辨证分析和数学处理。本文基于联系数，以一个简单的电子装备体系为例，如图1所示，对电子装备系统和体系作战效能的倍增效应进行初步的探讨；同类型电子装备为某一作战目标组成电子装备系统，图中的侦察装备、测向装备、干扰装备分别构成电子装备系统。

图1一种电子装备体系组成示例图

3　电子装备系统作战效能倍增效应分析

设有n（n≥2）个同类型电子装备为某一作战目标组成电子装备系统，这时作用在该目标上的总体作战效能等于所有电子装备的作战效能之合成。该系统中每一装备在发挥本身具备的作战效能，其作战效能在和其他n-1套装备作战效能合成时，并不是单纯的求和关系，因为电子装备在进行作战时存在电磁波传播衰减等很多不确定因素的影响，而且每一装备在和其他n-1套装备组成系统时还有相互的影响与制约等作用，这种影响作用也是很复杂的非线性关系，并不是一个简单的函数关系就能描述的。因此，在进行系统作战效能的合成时，同类型电子装备组成系统进行作战是一种并行关系，对组成系统的每一装备的作战效能描述时需要考虑上述不确定性，然后就可以简化认为系统的总体作战效能等于所有电子装备的作战效能之和。

根据该模型可以做如下的分析：

（1）当i→1时，表示系统作用的最理想状态，该状态下该系统中任何一套电子装备作战效能发挥对其他装备作战效能发挥都起到积极作用，每套装备电子装备都由于系统的作用而带来作战效能的倍增，此时装备系统的作战效能值为an（1+k）。由此可知，在理想状态下，一个由n（n≥3）套电子装备组成的电子装备系统的作战效能大于这n套电子装备单独作战时的作战效能之和an。当kmax=n-1时，装备系统的作战效能值为an2，是该系统中n套电子装备单独作战时的作战效能之和的n倍，这是系统的积极作用发挥到最大时的理想结果。

（2）当i=0时，表示该系统中任何一套电子装备系统作战效能的发挥对其他电子装备作战效能的发挥既不起积极也不起消极的作用，此时该模型的优化结果为an。这表明该系统中任何一套电子装备都在独立地发挥着作战效能，系统的作战效能仅仅等同于各个电子装备的个体作战效能之和，换句话说，这时毫无系统作战效能可言。

（3）当i→-1时，表示该系统中任何一套电子装备作战效能的发挥对其他电子装备作战效能的发挥只起消极的作用，装备成系统作战带来的作战效能起不到倍增的作用，倍增系数k→1+，此时该模型的优化结果为an（1-k），并有an（1-k）→0-，其趋近于0的含义是指系统的作战效能越来越难以发挥。也就是说，当i→-1时，系统中的这些电子装备不能“相互帮助”地实现作战效能的倍增作用，而是“相互拆台”、相互干扰，甚至使每套电子装备连其本身的正常作战效能也难以发挥；并且由an（1-k）→0-可以看出，n越大，系统效能an（1-k）越小，还不如

以作战能力指数衡量电子装备的作战效能，采用a+bi型同异联系数的形式进行描述，其中a表示电子装备本身具备的作战效能，b表示受其他电子装备影响而增加或衰减的作战效能，不确定性系数i在区间［-1，1］内取值。

在一般情况下，假设该系统中每套电子装备的作战效能为a+kai（1≤k≤n-1），其中k定义为装备成系统作战带来的作战效能倍增系数，则由n（n≥2）套电子装备组成的电子装备系统的作战效能为an+akni。将电子装备组成系统进行作战目的是为取得最大作战效能，也就是说，希望上述不确定性发挥积极的影响，针对不确定性系数i的取值，最好i能趋近于1取值。因此，得到该系统作战效能的优化模型为单套电子装备作战效能的发挥，因为系统的规模越大，系统中电子装备之间的“相互拆台”、相互干扰作用越大。

事实上，如果该系统中任何一套电子装备作战效能的发挥对其他装备作战效能的发挥起“相互帮助”的作用大于“相互拆台”的作用，即0＜i＜1时，有an+akni＞an（1+k）＞an，表明一个由n（n≥2）套电子装备组成的电子装备系统的作战效能大于这n套电子装备作战效能之和，起到了系统效能的作用。所以，如果确保电子装备工作时的相互干扰比较小，组成系统来工作时的系统作战效能比多套电子装备独立工作时的作战效能之和要大。

4　电子装备体系效能倍增效应分析

设有n（n≥3）个不同性能的电子装备系统为完成某一作战任务组成一电子装备体系，这时该体系中的任何一套电子装备系统所发挥的作战效能，除了装备系统本身具备的作战效能外，还受到其他n-1套装备系统的影响、制约等作用，但这种作用对该体系作战效能的发挥是积极还是消极，这些装备系统之间相互发挥作用是协同还是离心，或者两者都不是，则具有不确定性。体系中的这种不确定性因子用联系数表示为1+（n-1）i，其中i在区间［-1，1］内取值。

图1中是电子装备体系由位于某种战场环境中的1套电子侦察系统、1套电子测向系统和1套电子干扰系统基于信息系统构成，其中电子侦察系统由套电子侦察装备组成、电子测向系统由套电子测向装备组成、电子干扰系统由套电子干扰装备组成。本节的电子装备体系作战效能的倍增效应不考虑信息系统的作战效能，此时该体系的不确定性因子为1+2i。

假设电子侦察装备系统的作战效能为U1=a1n1+a1k1n1i、电子测向装备系统的作战效能为U2=a2n2+a2k2n2i、电子干扰装备系统的作战效能为U3=a3n3+a3k3n3i，则该电子装备体系的作战效能为

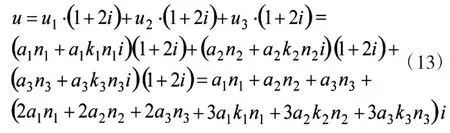
则有该体系作战效能的优化模型为

根据该模型依据i的取值可以做如下的分析：

（1）当i→1时，表示在正理想状态下，该体系中任何一套电子装备系统作战效能的发挥对其他装备系统作战效能的发挥都起积极的作用，此时体系的作战效能为

该体系中所有装备独立作战时其作战效能之和为

u'a1n1+a2n2+a3n3

令kmin=min{k1，k2，k3}，则有

由此可知，该电子装备体系的作战效能是该体系中所有装备作战效能之和的3（1+kmin）倍，远远大于这些装备的作战效能之和，充分说明了进行体系作战时装备作战效能的倍增效应。

在电子装备的体系作战效能实际发挥中，由于多种不确定性因素的存在，很难达到上述理想状态，但是一般能实现0＜i＜1，即该体系中任何一套电子装备系统作战效能的发挥对其他装备系统作战效能的发挥起积极作用大于消极作用，这时有

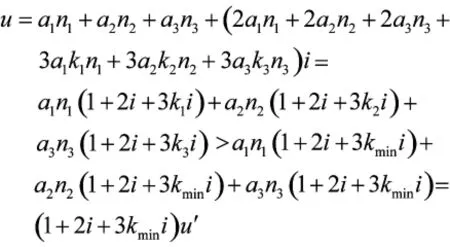
可以看出，该电子装备体系的作战效能大于这些装备独立工作时的作战效能之和，起到了体系效能的倍增作用。所以，在电子装备的作战使用上，如果确保它们工作时相互干扰比较小，装备之间“相互帮助”的作用大于“相互拆台”的作用，应该将多套电子装备组成体系来工作，避免多套装备独立工作的现象。

（2）当i=0时，表示该体系中任何一套电子装备系统作战效能的发挥对其他装备系统作战效能的发挥既不起积极也不起消极的作用，这时有

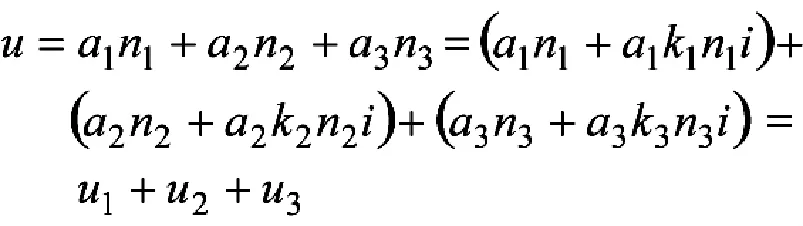
结合上一小节i=0时的分析结论，这表明该体系中任何一套电子装备都在独立地发挥着作战效能，体系的作战效能仅仅等同于各个电子装备的个体作战效能之和。

（3）当i→-1时，表示在负理想状态下，该体系中任何一套电子装备系统作战效能的发挥对其他装备系统作战效能的发挥只起消极的作用，此时

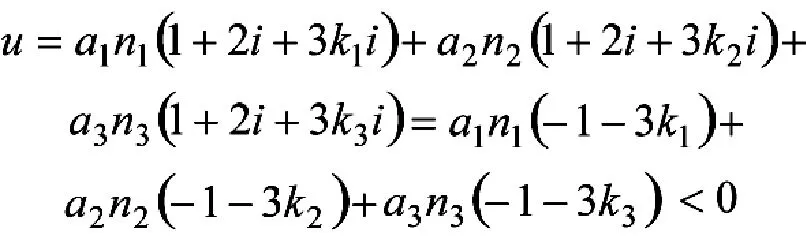
该式表明体系作战效能完全无法发挥（并不是表示作战效能为负数），而且电子装备体系的规模越大，即n1越大、或n2越大、或n3越大、或n1+n2+n3越大，体系作战效能无法发挥的程度越大，这时体系中装备系统或装备之间的“相互拆台”作用越大。

综上所述，基于联系数对体系作战效能进行分析，可以得到电子装备体系作战效能随不确定性系数的倍增效应示意图，如图2所示。

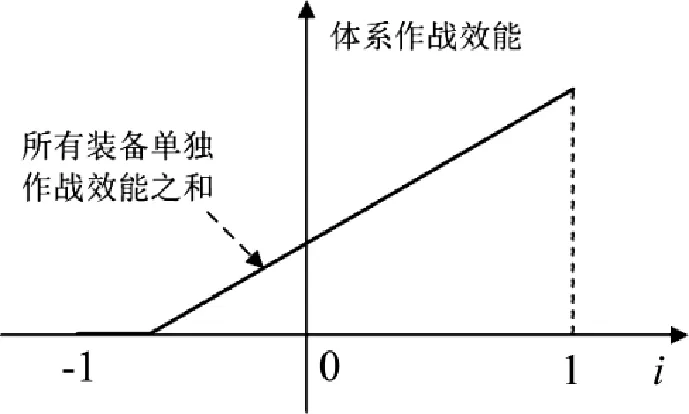
图2体系作战效能倍增效应示意图

5　基于联系数的电子侦察装备侦察能力分析

假设3套电子侦察装备E1，E2，E3对某个地域的t1，t2，…，t9，t10等10个目标进行侦察，假设侦察装备E1在不受任何影响的情况单独进行侦察，可以侦察识别t1，t2，t3，t4，t5等5个目标，有外界情报辅助时还可以侦察识别t6、t7、t8等3个目标，受到外界干扰仅能时侦察识别t3，t4，t5等3个目标；侦察装备E2在不受任何影响的情况单独进行侦察，可以侦察识别t2，t3，t4，t5，t7等5个目标，有外界情报辅助时还可以侦察识别目标t6、t8，受到外界干扰仅能时侦察识别t3，t4，t5等3个目标；侦察装备E3在不受任何影响的情况单独进行侦察，可以侦察识别t2，t3，t4，t5，t9，t10等6个目标，有外界情报辅助时还可以侦察识别目标t7、t8，受到外界干扰仅能时侦察识别t3，t4，t5，t9，t10等5个目标。

在上述假设条件下，以侦察识别目标的个数表示侦察装备的作战效能，则有电子侦察装备E1，E2， E3作战效能联系数表达式分别为

可以看出，当3套电子侦察装备E1，E2，E3都单独进行侦察（这时i1=0、i2=0），其作战效能之和为

u1+u2+u3=（5）+（5）+（6）=8

即最多能侦察到8个目标。

当3套电子侦察装备E1，E2，E3组成系统进行侦察，并假设3套装备相互起帮助促进作用，这时有i1=1、i2=0，其作战效能之和为

u1+u2+u3=（5）+（3）i1+（5）+（2）i1+（6）+（2）i1=10即最大能侦察到10个目标。

又当3套电子侦察装备组成系统进行侦察，并假设3套装备相互起“相互拆台”的反作用，这时有i1=1、i2=-1，其作战效能之和为

u1+u2+u3=（5）+（2）i2+（5）+（2）i2+（6）+（1）i2=5即在这种情况下仅能侦察到5个目标。

6　结论

本文提出了基于集对分析理论中联系数的电子装备系统和体系作战效能倍增效应分析新方法，分析结果表明：①于联系数对电子装备系统和体系作战效能倍增效应进行分析是有效可行的，该方法可以推广应用于其他武器装备体系作战效能分析活动中；②电子装备系统或体系作战效能的倍增是不确定的，在进行电子装备系统或体系设计与建设时，应该从整体上使装备要素之间的“相互帮助”作用大于“相互拆台”作用，这样才能获得倍增的总体作战效能；③当组成系统或体系的装备之间的相互干扰比较大时，宁可让这些装备独立工作，也不要组成系统或体系来工作，这时至少可以获得各个装备个体作战效能之和的总体作战效能。

参考文献：

［1］常显奇，程永生.常规武器装备试验学［M］.北京：国防工业出版社，2007．

［2］PITSKO R，VERMA D. System of system case study - why the network centric command and control system needed to change：lessons from army command and control in operation

iraqi freedom［C］// Proceedings of the 2011 6th International Conference on System of Systems Engineering，Albuquerque，New Mexico，USA，2011.

［3］LOREN J. System of system engineering for air force capability development［J/OL］. United States Air Force Scientific Advisory Board，2005［2014-4-9］.http：//www.dtic.mil/cgibin/GeTRDoc?AD=ADA442612.

［4］CROSSLEY W A. System of systems：an introduction of purdue university schools of engineering’s signature area［J/OL］. Software System Engineering，2002.http：//esd.mit.edu/symposium/pdfs/papers/crossley.pdf.

［5］LANE J A，BOHN T. Using SysML to evolve systems of systems［J/OL］.2010.http：//csse.usc.edu/csse/TECHRPTS/2010/ usc-csse-2010-506/ usc-csse-2010-506.pdf.

［6］DELAC G.System engineering guide for systems of systems［J/OL］.2009. http：//www.acq.osd.mil/se/docs/SE-Guide-for-SoS.pdf.

［7］BUDISELJ C I.The characteristics and emerging behaviors of system of systems［J/ OL］. 2005. http：//necsi.edu/education/oneweek/ winter05/NECSISoS.pdf.

［8］SMITH D. Analysis of system of systems［OL］. 2nd Annual System of Systems Engineering Conference，2006.http：//www. sosece.org/pdfs/2ndconference/Presentations/SoSECE% 20Breakout%20Day%202/Smith Wuenschel. pdf.

［9］李恒劭，秦立富.战场信息系统［M］.北京：国防工业出版社，2003.

［10］赵克勤.集对分析及其初步应用［M］.杭州：浙江科技出版社，2000．

［11］赵克勤，米红.非传统安全与集对分析［M］.北京：知识产权出版社，2010.

Multipactor Effect Analysis for Combat Efficiency of Electronic Equipment System of System Based on Connection Number

XIA Bin1，XU Yong2，KE Hong-fa3，HE Qi-hui1
（1. Luoyang Electronic Equipment Testing Center，Luoyang 471003，China；
2. Center for Engineering Design and Research under the General Equipment Department，Beijing 100028，China；
3. Science and Technology on Complex Electronic System Simulation Laboratory，Academy of Equipment，Beijing 101416，China）

Abstract：New multipactor effect analysis method for combat efficiency of electronic equipment system of system based on connection number is put forward. Firstly，the definition and arithmetic operations of connection number are introduced. Secondly，the connection number of similarity and difference type which based on combat efficiency index is proposed to describe the combat efficiency of electronic equipment. Then，multipactor effect of combat efficiency of electronic equipment system and system of system based on the value of the uncertainty coefficient are analyzed respectively. Finally，example of reconnaissance ability analysis of electronic reconnaissance equipments is given. And the feasibility and effectiveness of the proposed method were proved by the simulated example.

Key words：system engineering methodology，combat efficiency，multipactor effect，connection number，electronic equipment systems of system

作者简介：夏斌（1978-），男，江苏江阴人，硕士，工程师。研究方向：电子对抗训练、电子信息装备试验技术。

*基金项目：2012年度国家社会科学基金资助项目（12GJ003-102）

收稿日期：2015-01-10

文章编号：1002-0640（2016）02-0072-05

中图分类号：TN915

文献标识码：A

修回日期：2015-03-08