连续波强激光武器的动态毁伤概率数学模型*

王向民，王　军，郭　治

（南京理工大学自动化学院，南京　290014）



连续波强激光武器的动态毁伤概率数学模型*

王向民，王军，郭治

（南京理工大学自动化学院，南京290014）

摘要：在强激光武器的跟踪误差为均方可导、各态历经、零均值的正态过程的条件下，通过明晰的物理概念与严谨的数理演绎，导出了它的动态毁伤概率的级数表达式。通过算例探讨了动态毁伤概率的性质：它存在两个极大值所对应的随机穿越的自然频率，当跟踪系统工作在其中的非零频率上时，更具有快速反应能力；展现了跟踪误差的传递函数与动态毁伤概率间的定量关系。为论证、设计、检验强激光武器系统的动态毁伤概率提供了理论依据与技术支持。

关键词：强激光武器，跟踪误差，随机穿越特性，毁伤概率

0　引言

连续波强激光武器作为精确、高效定点杀伤武器，已成为战术武器系统的发展前沿而受到极大的重视。装载在运载体上的连续波强激光武器在对运动目标实施射击时，在相同的毁伤定义下，只有它的毁伤概率优于现有担负同类任务的其他类型的武器，才有成为列装武器的可能。如果将强激光载体与其射击的目标存在相对运动时的毁伤概率称为强激光武器的动态毁伤概率，显然，建立这种动态毁伤概率的数学模型，对论证、设计、检验强激光武器都是一项基础性重要任务。文献［1-3］对动态毁伤概率进行了仿真研究，其中也提到了对它的数学模型的急切需求，但至今未见这一数学模型的相关文献。

当用静止强激光对准一个固定目标直接照射时，不同特性的强激光在不同的环境下，对不同材质目标毁伤能力的特性，谓之强激光的静态毁伤特性。有关这种特性的研究文献颇多，其中文献［4］以可信的理论分析和大量的试验成果概括出了一条具有普适性的、有关连续波强激光的静态毁伤特性：在确定的环境中对特定材质的目标直接照射一确定的时间（致毁时间）Th后，即可导致该目标毁伤；倘若上述条件发生确定性改变，只是致毁时间发生相应的变化；强激光致毁目标的时间很短，目标由于温升而致毁的过程可近似一个绝热过程，即在一个允许的时间内，致毁时间可以分解为多个时段依次辐照，只要总的辐照时间不变，毁伤效果亦不变。本文在上述静态毁伤特性的支持下，推导出了动态毁伤概率并通过算例分析了它的性质。

1　致毁条件

为达到动态毁伤，本文提出了3个武器系统必须满足的致毁条件：

条件1：连续波强激光光束覆盖目标上一个固定的待毁中心O的总时间超过致毁时间Th，目标将被毁伤。

条件2：强激光束的跟踪误差，即激光束中轴相对待毁中心O的方向角误差Z（t）=（x（t），y（t））T为相互独立的二维、均方可导、各态历经、零均值的正态过程。

当强激光武器载体的稳定系统与目标跟踪系统均采用无偏估计与无偏控制策略，且射击过程在过渡过程结束后实施时，上述条件是完全可以接受的。又由随机过程理论可知，各态历经、均方可导、零均值的正态过程的导数依然是各态历经、零均值的正态过程，且与原函数相互独立，故x（t），y（t），（t），（t）都是相互独立的的，其联合密度函数

式中：σx，σy为x（t），y（t）的均方差；σx，σy为（t），（t）的均方差。

强激光束的束散角记为2ρ，以待毁点O为中心，半径等于ρ的圆称为射击门，显然，跟踪误差Z（t）可能以不同的随机轨迹穿越射击门，如图1所示。

图1射击门与跟踪误差的示意图

图中φ为ρ与x方向的张角。而tin，i={t2i-1-t2i-2；i=1，2，…}为辐照时间，一般文献上称为滞留时间。而tout，i={t2i-t2i-1；i=1，2，…}为失照时间，一般文献称为待机时间，又tch，i=tin，i+tout，i={t2i+1-t2i-1；i=1，2，3，…}为随机周期。很明显，tch，i，tin，i和tout，i都是随机变量。

条件3：强激光在t=t0瞬时发射，在t-t0=Ts＞Th＞0时结束。

欲保证在t=t0瞬时发射强激光，必须设置一个能检测到跟踪误差Z（t）穿入射击门瞬时的装置，例如一直跟踪目标的弱激光跟踪装置。

在满足上述条件下，如果在t∈［0，Ts）的时间内，存在一个n，使

则目标必然毁伤。推导此公式在3个致毁条件下的概率即是本文的中心命题。

2　对射击门随机穿越的自然频率

单位时间内，跟踪误差对射击门的随机穿越周期的平均个数称为跟踪误差对射击门随机穿越的自然频率，它是表征随机穿越快慢的一个特征参数。仅有（（t）（t））T在射击门半径方向上的分量与φ的分布特性才影响随机穿越的次数，而与无关，故记

显然

又由于（x，y）在φ方向上的密度函数为瑞利分布，即

因而，在所有φ∈［0，2π）上随机周期在单位时间内出现的平均个数

式中

为虚自变量第一类贝塞尔函数的展开式，它收敛极快。

若σx=σy时，有

3　 n个随机穿越周期的密度函数

设α0为跟踪误差覆盖射击门区域的概率，则有

为跟踪误差在射击门内的概率。当σx=σy时，有

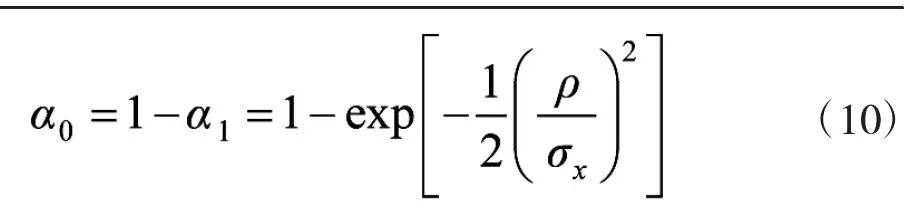
对均方可导、且各态历经的零均值的二维正态过程，当已知α0与λ，由文献［5-6］可知，其单个辐照时间的密度函数服从指数分布

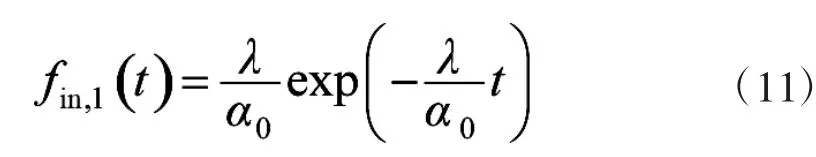
n个辐照时间的密度函数服从Γ分布

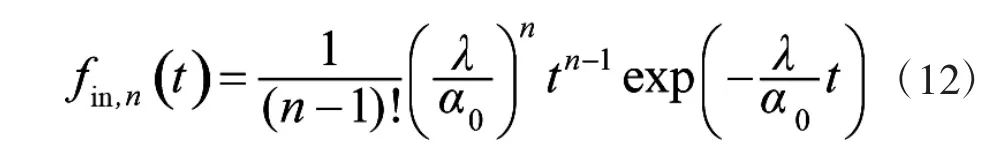
若将上述两式中的α0置换为α1，则得到对应的失照时间的密度函数。单个随机周期的密度函数

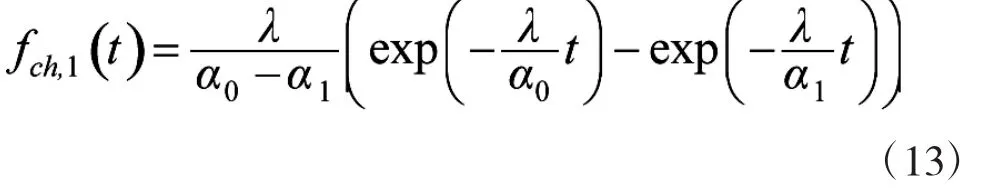
考虑到n个独立随机周期的密度函数等于一个随机周期的密度函数的n-1次卷积，又由于一个随机周期的密度函数存在拉普拉斯变换，依据拉普拉斯变换的卷积定理，有n≥1个随即周期的密度函数

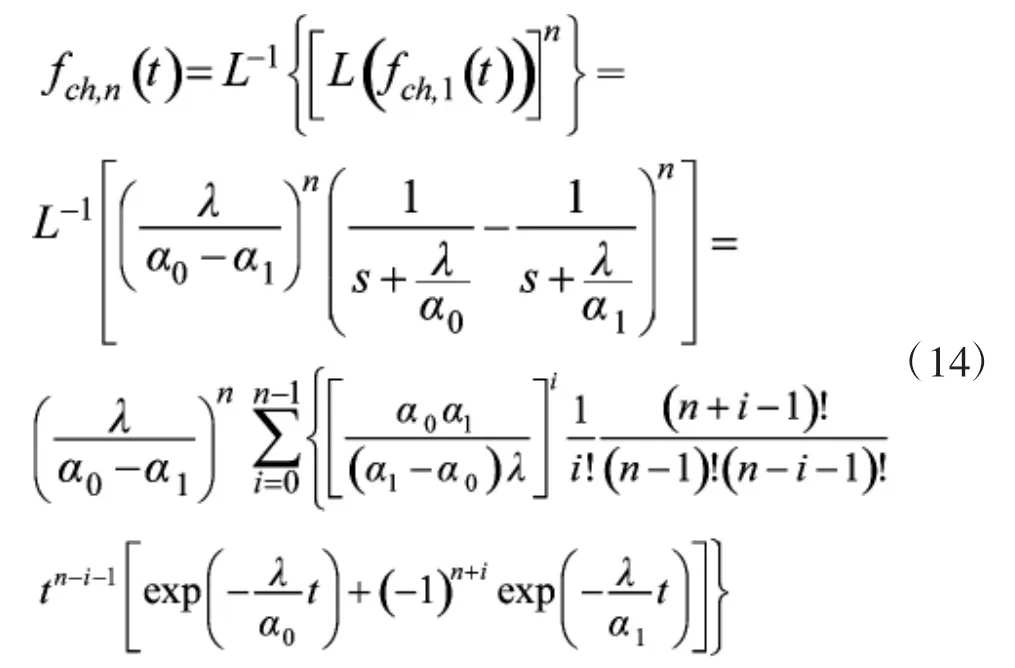
由于致毁条件3要求强激光发射从Z（t）穿入射击门开始，因而，必然有一个服从指数分布的辐照时间tin，1，当发射时间Ts＜tin，1时，Z（t）不存在随即周期，故有零随机周期的密度函数

式（14）、式（15）共同构成了n个随机周期的密度函数，如下页图2所示。

显然，不论n≥0为多少，n个随机周期的长度的取值范围都是［0，∞）。

图2随机周期的密度函数

强激光武器的动态毁伤概率指的是在发射前对射击过程中所存在的辐照时间之和不小于致毁时间的概率的预测值。根据致毁条件3，强激光的发射瞬时应处于Z（t）对射击门的穿越点，因而，必然进入一个由辐照时间构成的零随机周期，之后继之以失照时间与辐照时间交替更新的非零随机周期。由于每个周期的历时都是随机的，因而任何随机周期都有可能结束于停止发射的瞬时。图3给出了n=0，1，2的示意图：

图3随机穿越周期示意图

由于强激光发射后，首先进入一个服从指数分布的零随机周期，若随机的tin，1不小于致毁时间，即tin，1≥Th（16）则目标必毁，此时的毁伤概率

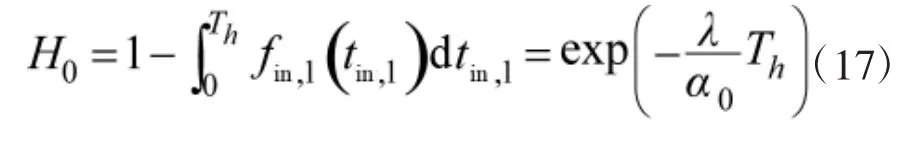
当第一个辐照时间未达到毁伤阈值时，若要在激光一次发射时间内使累积辐照时间大于毁伤阈值Th，则至少会出现一个完整的随机周期。而强激光的一次射击过程可以认为是由辐照时间和失照时间两种状态（状态0和状态1）构成的齐次马尔可夫链，且开始于辐照时间状态，若令P（t）为转移概率阵

依连续时间马尔可夫链的定义及性质可得若随机的tin，1小于致毁时间，可求得［7］

和

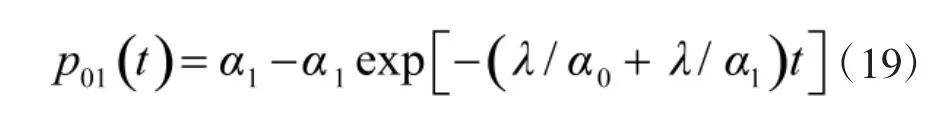
式（18）和式（19）分别表示激光束在Ts时刻时，处于射击门内和射击门外的概率。考虑到以随机周期的计数过程作为更新过程，利用更新过程的性质，可以求的在t∈［0，Ts］时间内，随机周期可能出现的个数概率为

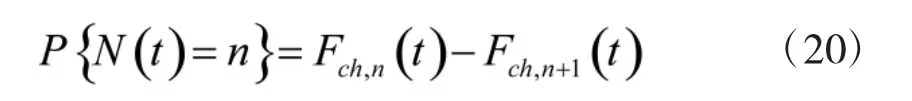
运用全概率公式，则强激光武器的动态毁伤概率表达式为

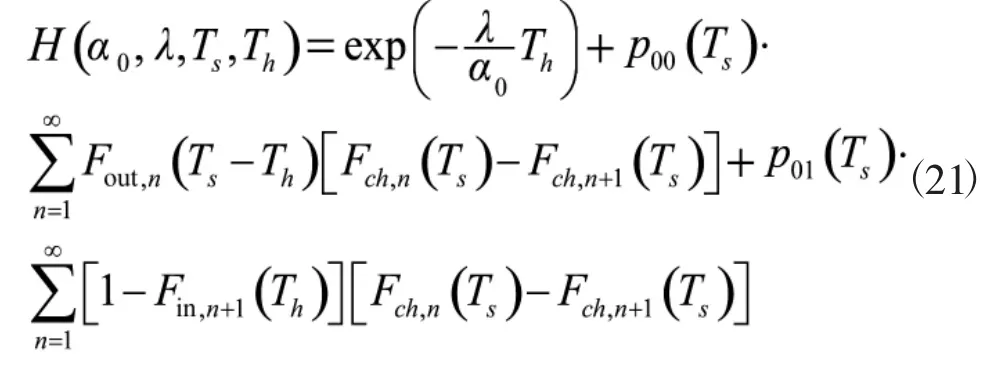
式中

和

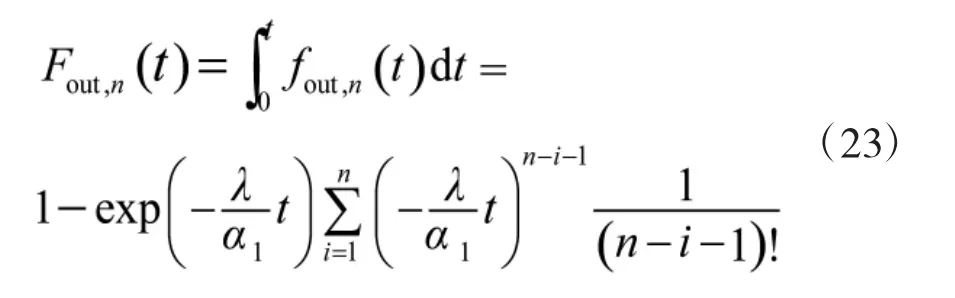
以及

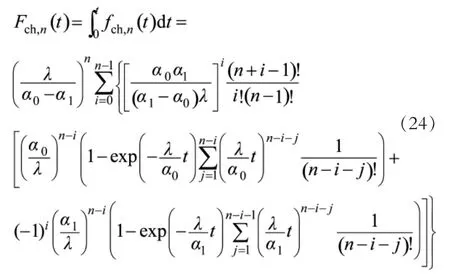
在利用式（21）计算动态毁伤概率时，当α0=α1=0.5时，由于辐照时间与失照时间的密度函数相等应以代替式（24）实施运算，以避免分母出现零值。

4　示例

示例1设Ts=4，Th=2.5，α0=0.6，当λ∈［0.1，4］时，利用式（21）计算动态毁伤概率如图4所示。

图4动态毁伤概率H随自然频率λ变化图

此示例表明，动态毁伤概率是自然频率λ的函数，且存在两个极大值。其中λ=0对应于跟踪误差为强相关误差，尽管可以在零值附近设置λ，但Z（t）当在射击门外时，却难以尽快地进入射击门实施射击，而另一个非零自然频率所对应的极大值却可以避免上述缺憾。

示例2设圆形射击门半径ρ=1，Ts=4 Th=2.5；wx（s）=wy（s）=为跟踪误差的白化后的整形滤波器，Φx（s）=Φy（s）=为跟踪系统的误差传递函数；以其输出的不相关的各态历经函数x（t），y（t）作为在两个方向上的跟踪误差的模拟量，当T1=0.1时，选取T2∈［0.1，6］时，利用式（5）即可得到动态毁伤概率随T2的变化，如图5所示。

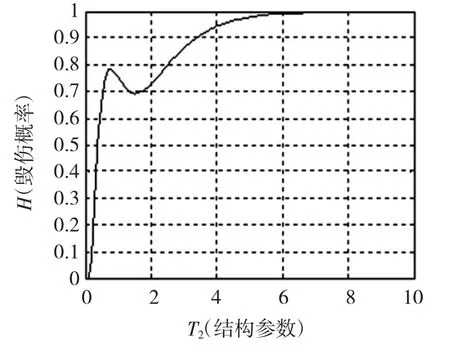
图5动态毁伤概率随T2的变化

从图中可以发现，当T2=2.126时，动态毁伤概率取得局部极大值。由于它对应的λ=1.561，因而具有快速进入射击门的能力。

此示例表明，动态毁伤概率在静态毁伤特性一定时，还直接决定于武器跟踪系统的动态特性及目标的机动特性。因而，该公式可以用以论证与设计连续波强激光武器系统的估计与控制策略，对动态毁伤概率进行优化。

5　结论

由于在公式演绎过程中所引用的物理概念均有确切随机理论支持，其间未引用经验数据与近似公式，因而只要强激光武器在运行中满足本文给出的3个致毁条件，所得结论是无误的；由于本文导出的动态毁伤概率所需的原始数据包含有武器系统稳态跟踪误差及其导数的方差，因而，它不仅可以作为动态毁伤概率论证的依据，而且可以直接与强激光武器系统的传递函数或状态方程结合在一起，以动态毁伤概率为目标函数，优化控制策略。

当武器系统的运行环境相对本文给出的致毁条件发生变化，例如，目标与武器的距离发生变化时，目标散热现象明显时，多个强激光束同时发射时，则应依具体变化状态，对本文给出的动态毁伤概率公式作必要修正。

参考文献：

［1］李勇，汪民乐，张均.高能激光武器对弹道导弹毁伤能力研究［J］.红外与激光工程，2006，35（5）：588-592.

［2］冯国斌，杨鹏翎，王群书，等.强激光远场光斑强度分布测量技术［J］.强激光与粒子束，2013，25（7）：1615-1619.

［3］吴艳梅，李俊昌.高能激光武器热毁伤仿真研究［J］.电光与控制，2009，16（2）：33-35.

［4］李清源.强激光对飞行器的毁伤效应［M］.北京：中国宇航出版社，2012.

［5］康正亮，胥凯晖，杨传超.ANFIS在航材需求量预测中的应用［J］.四川兵工学报，2015，34（1）：84-87.

［6］朱位秋.随机振动［M］.北京：科学出版社，1992.

［7］KARLIN S，TAYLOR H M.随机过程初级教程［M］.北京：人民邮电出版社，2007.

Mathematical Model for Dynamic Damage Probability of the CW High- energy Laser Devices

WANG Xiang-min，WANG Jun，GUO Zhi
（School of Automation，Nanjing University of Science and Technology，Nanjing 210094，China）

Abstract：Aimed at the CW high-energy laser devices，under the assumption that the tracking error is the normal stochastic process of mean square differentiability and ergodicity，the Series Expression of the dynamic damage probability was given. The examples demonstrate some characteristics of the dynamic damage probability as follow. First there exists natural frequencies of stochastic passage relevant to two different maximums. Second，the tracking system has a more rapidly response to non-zero frequencies. At last，the system proposed indicates the quantitative relationship between dynamic damage probability and transfer function of the tracking error system，which offers theoretical and technological support on proofing，designing and testing the dynamic damage probability of CW high-energy laser devices.

Key words：CW high power laser，tracking error，stochastic passage characteristic，damage probability

作者简介：王向民（1975-），男，湖南华客人，博士生，助理研究员。研究方向：火力控制。

*基金项目：国家自然科学基金（61104197）；国家部委预先研究基金资助项目（40405070103）

收稿日期：2015-01-09

文章编号：1002-0640（2016）02-0055-05

中图分类号：TP273，TJ95

文献标识码：A

修回日期：2015-03-11