基于shearlet与PCNN的多聚焦图像融合方法*

牛　玲，冯高峰

（1.周口师范学院，河南　周口　466001；2.济源职业技术学院，河南　济源　454650）



基于shearlet与PCNN的多聚焦图像融合方法*

牛玲1，冯高峰2

（1.周口师范学院，河南周口466001；2.济源职业技术学院，河南济源454650）

摘要：针对传统脉冲耦合神经网络（PCNN）模型在多聚焦图像融合领域应用中面临的参数繁杂等问题，提出一种基于剪切波（shearlet）变换与改进型PCNN的多聚焦图像融合方法。相比以往的变换域方法，shearlet具有理想的图像信息捕捉性能以及较低的计算复杂度，因此，可利用shearlet将待融合图像进行多尺度多方向分解。其次，对经典PCNN模型加以改进，综合运用清晰度水平以及协调矩阵完成低频子带图像以及一系列高频子带图像的融合过程。最后，运行shearlet反变换得到最终融合图像。仿真实验选取了若干组待融合图像进行仿真，验证了该方法在主、客观评价两方面的优越性。

关键词：剪切波变换，脉冲耦合神经网络，协调矩阵，清晰度

0　引言

成像设备中焦距的不同通常会使图像中的目标信息出现分化，即部分目标较为清晰处于聚焦状态，而另外一部分目标处于离焦状态较为模糊。

目前，国内外相关领域的学者针对多聚焦图像融合问题，提出了一系列融合方法。见文献［1-11］。本文拟将ST与PCNN模型相结合，提出一种基于shearlet与改进型PCNN模型的多聚焦图像融合方法。该方法针对传统PCNN模型待定参数多、运行机制复杂的问题加以改进，综合运用清晰度水平以及协调矩阵完成低频子带图像以及一系列高频子带图像的融合过程。仿真实验结果表明，该方法在主、客观评价过程中均有良好表现。

1　剪切波变换

Guo等人在文献［8-12］中指出，当维数n=2时，可以得出以下仿射系统模型：

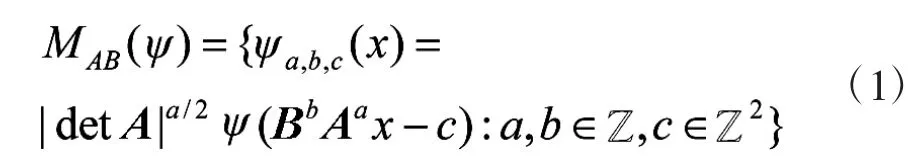
其中，ψ∈L2（R2），Aa与Bb均为2*2的可逆矩阵，且满足表达式|detB|=1。若MAB（ψ）满足帕斯维尔理论紧框架，即满足：

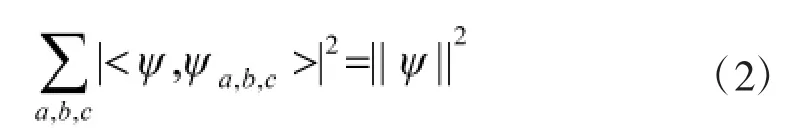
则该仿射系统中的元素可称作合成小波。

合成小波同经典离散小波变换理论类似，满足多尺度分析特性，因此，可以给出剪切波变换的定义：令ψ∈L2（R2）满足下列条件：

其中ψ赞为ψ的傅里叶变换；

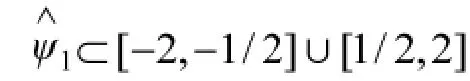
③若ψ赞2∈C∞（R）且suppψ赞1奂［-1，1］，且在区间（-1，1）上满足ψ2>0且||ψ2||=1，则由ψ，Aa，Bb可以生成下列系统：

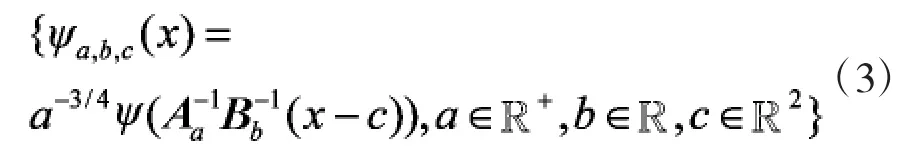
其中，Aa=［a 0，0 a1/2］，Bb=［1 s，0 1］，式（3）即为shearlet系统，Aa和Bb分别为各向异性膨胀矩阵和剪切矩阵。

通常，可取a=4，s=1，即：

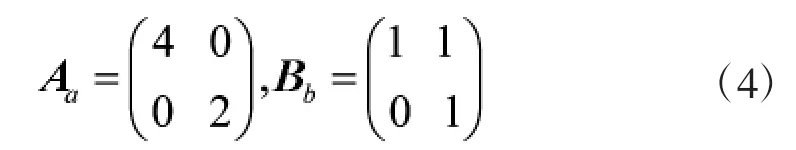
2　改进型PCNN模型

PCNN模型有着广泛的生物学背景，其数学表达式如下：

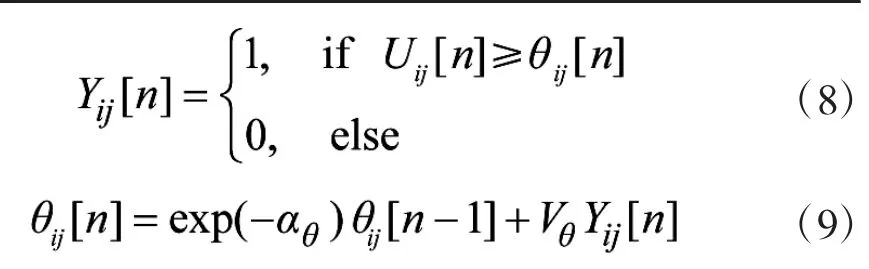
显然，经典PCNN模型中大量存在的待定参数以及过于繁杂的工作机制导致其优势无法大幅度地发挥，为此，本文提出一种改进型PCNN模型，其数学表达式如下：

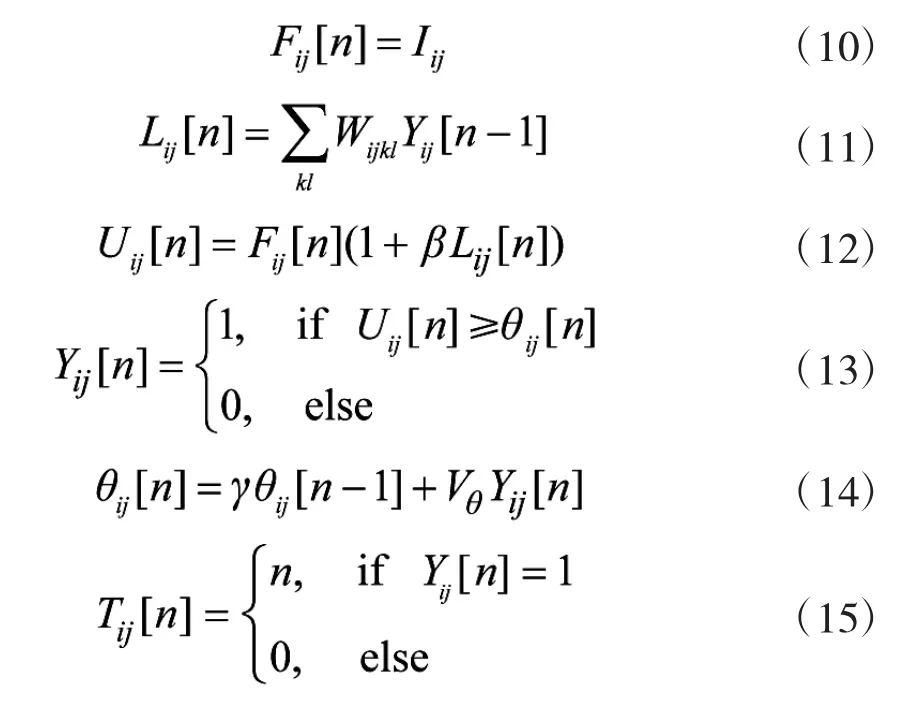
其中式（10）忽略了前一次的馈送效果值以及输出结果矩阵对本次馈送输入的影响，仅仅考虑外部输入的效果；式（11）仅对上一次的输出效果矩阵进行了记录；式（14）有助于解决以往模型中阈值衰减速率及幅度不稳定的缺陷；此外，迭代效果的好坏在很大程度上取决于迭代次数的设置。如果迭代次数K的数值过大，将会白白浪费大量的计算资源；反之，如果迭代次数K的数值设定过小，又会导致算法运行的不充分，难以获得令人满意的运行结果。式（15）则是借鉴文献［13］中赋时矩阵的概念，依靠神经元自身的同步脉冲发放机制自适应地决定迭代次数n的数值。赋时矩阵T将对每一个像素点的发放脉冲时对应的迭代次数加以记录，并且保证每一个像素点在发生点火后，点火阈值急剧增大从而不再被激发，即每个像素点仅点火1次。当所有的像素点均完成脉冲发放即脉冲输出矩阵Y=1时，迭代过程自行停止。

不难发现，本文提出的改进型模型仅涉及Wijkl，β，γ和Vθ4个待定参数。由于赋时矩阵机制的引入，为了保证每个像素点对应的神经元仅进行一次点火，只需将式（14）中的Vθ赋予一个较大的数值即可，因此，待定参数Vθ的数值也容易设定。

（1）Wijkl：该矩阵用于设定神经元间的关联程度，重点描述周围神经元的输出情况对中心神经元的影响程度，通常认为：中心神经元的水平及垂直方向上直接相邻的神经元对中心神经元有较大的影响，而45°、135°、225°以及315°方向上相邻的神经元影响较弱，因此，以3*3区间为例，可以设定水平及垂直方向上的神经元间隔距离为1，则Wijkl可以设定为：

（2）γ：主要功能是用来控制阈值的衰减幅度。该参数的设定主要取决于源图像中灰度分布的情况。如果一幅图像的灰度分布较为均匀且纹理较为单一，则可以适当减小γ的数值，提高实验速率；反之，如果一幅图像的灰度变化较为剧烈，则应当赋予γ一个较大数值，从而尽可能地把握灰度剧变过程中的边界信息。

（3）β：用来反映馈送域输入与链接域输入的耦合程度，β的数值越大，链接域输入的作用就越大，内部连接U的数值也越大。由于多聚焦图像融合的主要目的是将多幅待融合源图像中的聚焦区域即清晰区域加以提取并注入到最终融合图像中，为此，本文采取自适应取值方法，以清晰度水平作为标准对每个像素点对应的神经元链接强度β进行赋值。

由于图像空间频率（Spatial Frequency，SF）的大小可以较大程度地反映图像中各像素点的活跃程度，因此，SF数值较大的像素点往往可以表示该像素点与周围像素点具有明显不同的活跃水平，即“异常突出的或清晰的”，因此，本文采用SF作为清晰度指数对链接强度β进行赋值。文献［14］给出了SF的数学表达式：

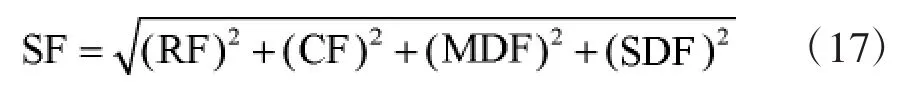
其中，RF表示水平方向的梯度值，CF表示垂直方向的梯度值，MDF表示主对角线方向的梯度值，SDF表示副对角线方向的梯度值。4种方向上的梯度示意图如图1所示。

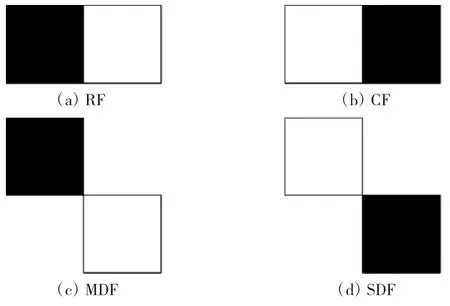
图1 SF的4个方向梯度分量

其中白色方框代表待考察中心像素点，黑色方框代表其相邻的像素点。4种方向的梯度表达式如下所示。

针对图像I（i，j），分别有RF，CF，MDF以及SDF的表达式如下：

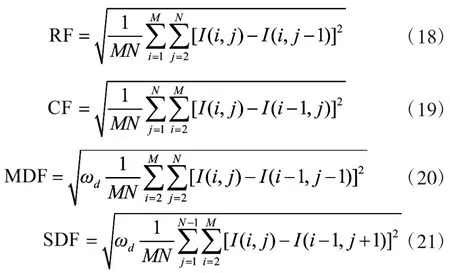
其中，ωd表示距离权值，可以取1/21/2。

显然，SF可以针对对应像素点的周边像素信息进行较为详尽的描述。

3　协调矩阵构造

大多数基于像素点的图像融合方法仅负责从各幅源图像中提取出相关像素点并加以融合，并不考虑融合结果图像中像素点间的协调程度，因此，常常会导致“人为虚假边缘”的产生，例如重影、块状反应等。为此，本文提出一种协调矩阵C用于对结果图像进行局部调整，从而实现融合后图像直觉效果的改善。

协调矩阵C将某一中心像素点周围的像素点成员划分为近域成员N和远域成员D，其中近域成员N对中心像素点具有较大的影响能力，而远域成员D对中心像素点影响较弱。以5*5邻域区间为例，具体影响因子（Impact Factor，IF）赋值如下所示。

在式（22）中，将中心像素点相邻的8个像素点视为近域成员N，这8个成员距离中心像素点仅有1个步长的距离；而将除了这8个近域成员之外的16个像素点视为远域成员D，这些成员距离中心像素点均有两个步长的距离。协调矩阵算法如下所示。

输入：初始邻域空间半径r，由两幅源图像A，B得出的初步融合结果图像；

输出：协调矩阵机制处理后的融合图像；

步骤1：比较中心像素点a的近域成员，若NA＞NB，则中心像素点a应来源于源图像A，并转向步骤6；否则，转向步骤2；

其中，NA，NB分别表示近域成员中来自于源图像A和B的数目；

步骤2：若NA＜NB，则中心像素点a应来源于源图像B，并转向步骤6；否则，转向步骤3；

步骤3：若NA=NB，则比较中心像素点a的远域成员。若DA＞DB，则中心像素点a应来源于源图像A，并转向步骤6；否则，转向步骤4；其中，DA，DB分别表示远域成员中来自于源图像A和B的数目；

步骤4：若DA＜DB，则中心像素点a应来源于源图像B，并转向步骤6；否则，转向步骤5；

步骤5：若DA=DB，则扩充邻域空间半径r，使得r=r+2，并转向步骤3；

步骤6：算法结束，并输出最终融合图像。

4　基于ST域改进型PCNN的图像融合算法

本节以两幅已配准待融合多聚焦源图像A和B的仿真过程为例，给出基于shearlet域改进型PCNN的多聚焦图像融合算法。具体的实现流程图如图2所示。

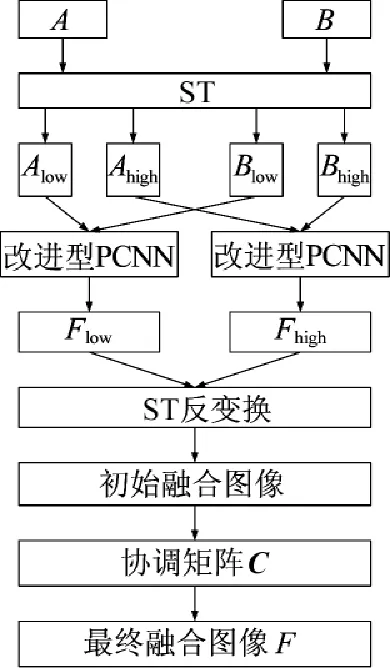
图2基于shearlet域改进型PCNN的多聚焦图像融合过程图

融合算法的具体步骤如下：

输入：两幅已配准源图像A，B；

输出：最终融合图像F；

步骤1：利用ST将源图像A，B各自分别分解为低频子带图像Alow（K），Blow（K）以及一系列高频子带图像Ahigh（k，lk），Bhigh（k，lk）；

其中，K为尺度分解级数，lk表示k尺度下l方向分解，1≤k≤K；

步骤2：将各子带图像对应像素点的灰度值的绝对值作为外部输入I，经由改进型PCNN模型加以处理，得到融合后的低频子带融合图像和一系列高频子带融合图像；

步骤3：进行ST反变换得到初始融合图像；

步骤4：利用第3节的协调矩阵算法对初始融合图像加以处理，获取最终融合图像F。

5　仿真实验与分析

5.1实验描述

为了验证本文方法的有效性和可行性，本节选取了两组待融合多聚焦源图像进行仿真实验。所有仿真平台为一台配置为2.3 G CPU和2 G内存的个人PC。选取了3种多聚焦图像融合方法与本文方法进行比较，分别为：方法1（ST与改进PCNN的融合方法）［12］；方法2（自适应PCNN的形态小波多聚焦图像融合方法）［14］；方法3（基于小波变换的多聚焦图像融合新算法）［15］。本文方法的参数设置情况如下：Wijkl=［0.707 1.000 0.707；1.000 0.000 1.000；0.707 1.000 0.707］，Vθ=300，γ=0.85。

针对实验仿真结果，除了进行直观视觉评价方法外，还将选取信息熵（IE）、边缘强度（EIN）、空间频率（SF）三项指标进行客观评价。其中，IE描述了图像中信息量的包含程度，IE数值越大，图像的信息越丰富。EIN表示图像中边缘特征信息的保持程度，EIN的指标值与图像边缘细节信息的保持状况成正比。SF反映了整幅图像的活跃程度，SF数值越大，整幅融合图像越清晰。

5.2实验结果与分析

本文选取了两组待融合多聚焦源图像用于仿真实验，分别是Clock图像以及Pepsi图像。这两组源图像均含有256级灰度，尺寸大小为512*512。两组待融合多聚焦源图像如图3所示。4种融合方法的仿真结果如下页图4、图5所示。

图3两组待融合多聚焦源图像

图4 Clock待融合多聚焦源图像仿真结果

图5 Pepsi待融合多聚焦源图像仿真结果

从整体上，4种多聚焦图像融合方法对图3中的两组待融合源图像均进行了较好融合，源图像中的主体信息得到了有效地提取和描述。图3中的主干信息在仿真结果中均得到了不同程度的体现。

但通过仔细观察后不难发现，基于本文提出方法的融合结果图无论在图像清晰程度还是源图像信息保持上均具有很明显的优势。为了进一步比较仿真结果，以图5中的仿真结果为例，给出了局部放大图像，如图6所示。

通过比较红色区域中的细节信息，可以发现，相比其他3种图像融合方法，基于本文方法的融合图像具有更好的清晰度水平。此外，相关的客观评价结果如表1、表2所示，实验结果验证了本文方法的有效性。

图6仿真结果局部放大图

表1 Clock融合实验客观指标结果

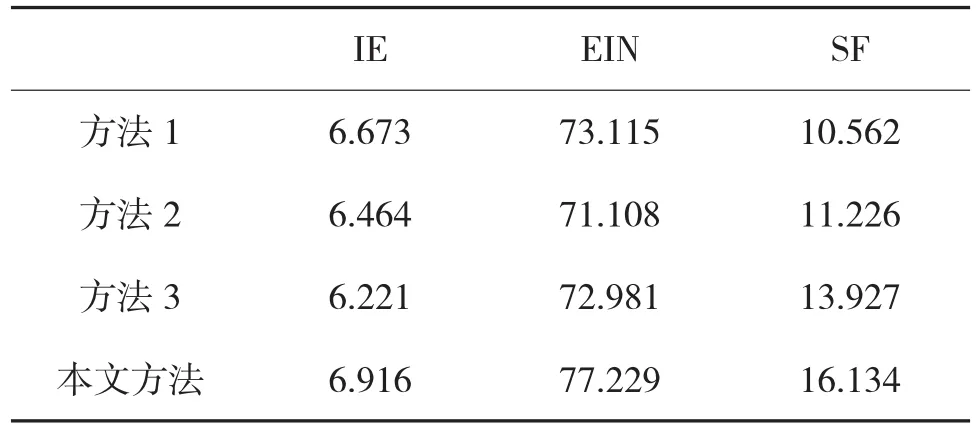
表2 Pepsi融合实验客观指标结果

6　结论

相对之前的变换域方法，ST具有更好的图像信息捕捉能力和较低的计算复杂度，因此，能够很好地适用于实时性要求较高的应用场合。另一方面，PCNN模型作为一种具有丰富生物学背景的人工神经网络模型，已被广泛应用于图像融合领域。本文提出一种基于shearlet与改进型PCNN的多聚焦图像融合方法，旨在将ST与PCNN二者的优势相结合，探索一种融合性能更为优越的多聚焦图像融合方法。两组融合实验验证了本文提出方法的有效性和优越性。

参考文献：

［1］CHAI Y，LI H F，LI Z F. Multifocus image fusion scheme using focused region detection and multiresolution［J］. Optics Communications，2011，284（19）：4376-4389.

［2］TAO W，ZHU C C，QIN Z C. Multifocus image fusion based on robust principal component analysis［J］. Pattern Recognition Letters，2013，34（9）：1001-1008.

［3］ZHAO H J，SHANG Z W，TANG Y Y，et al. Multi-focus image fusion based on the neighbor distance［J］. Pattern Recognition，2013，46（3）：1002-1011.

［4］ISHITA D，BHABATOSH C. Multi-focus image fusion using a morphology-based focus measure in a quad-tree structure ［J］. Information Fusion，2013，14（1）：136-146.

［5］ZHANG Y X，CHEN L，ZHAO Z H，et al. Multi-focus image fusion based on robust principal component analysis and pulse-coupled neural network［J］. Optik，2014，125（17）：5002-5006.

［6］ECKHORN R. Neural mechanisms of scene segmentation：recordings from the visual cortex suggest basic circuits or linking field models［J］. IEEE Transactions on Neural Network，1999，10（3）：464-479.

［7］MIAO Q G，SHI C，XU P F，et al. A novel algorithm of image fusion using shearlets［J］. Optics Communications，2011，284 （6）：1540-1547.

［8］GUO K H，LABATE D. Optimally sparse multidimensional representation using shearlets［J］. SIAM Journal on Mathematical Analysis，2007，39（1）：298-318.

［9］GUO K H，LABATE D，WANG L. Edge analysis and identification using the continuous shearlet transform［J］. Applied and Computational Harmonic Analysis，2009，27（1）：24-46.

［10］LIU X，ZHOU Y，WANG J J. Image fusion based on shearlet transform and regional features［J］. International Journal of Electronics and Communications，2014，68（6）：471-477.

［11］SHI C，MIAO Q G，XU P F. A novel algorithm of remote sensing image fusion based on Shearlets and PCNN［J］. Neurocomputing，2013，117（6）：47-53.

［12］廖勇，黄文龙，尚琳，等. Shearlet与改进PCNN相结合的图像融合［J］.计算机工程与应用，2014，50（2）：142-146.

［13］刘勍，马义德.一种基于PCNN赋时矩阵的图像去噪新算法［J］.电子与信息学报，2008，30（8）：1869-1873.

［14］何刘杰，胡涛，任仙怡.自适应PCNN的形态小波多聚焦图像融合方法［J］.计算机工程与应用，2013，49（12）：132-135，159.

［15］韩潇，彭力.基于小波变换的多聚焦图像融合新算法［J］.计算机与数字工程，2014，42（9）：1628-1631.

Fusion Method for Multi- focus Images Based on Shearlet and Pulse Coupled Neural Networks

NIU Ling1，FENG Gao-feng2
（1.Zhoukou Normal University，Zhoukou 466001，China；2. Jiyuan Vocational And Technical College，Jiyuan 454650，China）

Abstract：In order to settle the problem that there are so many parameters in the Pulse Coupled Neural Networks（PCNN）model when used in the area of multi-focus image fusion，a fusion method for multi-focus images based on shearlet transform and improved PCNN is proposed. Compared with the past transform domain methods，shearlet possesses much better ability to capture the image information and much lower computational complexities，so it can be used to conduct the multi-scale and multi-directional decompositions towards the source images. Besides，with the definition level and coordinate matrix，the classic PCNN model can be improved to fuse the low-frequency sub-images and a series of high -frequency ones. Finally，the final fused image can be obtained with the inverse shearlet. Several different groups of source images have been chosen in the simulation experiments，the proposed method proves to be superior in both subjective and objective aspects.

Key words：shearlet transform，pulse coupled neural networks，coordinate matrix，definition level

作者简介：牛玲（1980-），女，河南周口人，硕士，主任。研究方向：图像处理、网络安全。。

*基金项目：国家自然科学基金（61103143）；河南省高等学校重点科研基金资助项目

收稿日期：2015-01-05

文章编号：1002-0640（2016）02-0041-06

中图分类号：TP182

文献标识码：A

修回日期：2015-03-09