面向多平台多目标协同跟踪的指派问题*

宋志强，周献中，徐　锋

（1.南京大学工程管理学院，南京　210093；2.苏州经贸职业技术学院机电与信息技术学院，江苏　苏州　215009；3.北方自动控制技术研究所，太原　030006）



面向多平台多目标协同跟踪的指派问题*

宋志强1，2，周献中1，徐锋3

（1.南京大学工程管理学院，南京210093；2.苏州经贸职业技术学院机电与信息技术学院，江苏苏州215009；3.北方自动控制技术研究所，太原030006）

摘要：针对多平台多目标协同跟踪中要求多个无人地面平台尽可能均匀地协同跟踪多个目标的特点，提出了改进的离散粒子群优化算法。首先采用连续型粒子群优化算法中的速度和位置迭代公式，然后对粒子位置进行离散编码，使粒子编码对应于可行的指派方案；其次，在优化算法中引入局部搜索，提高算法寻优性能。最后将所提算法应用于多平台多目标协同跟踪中的指派问题，并与未加入局部搜索的粒子群优化算法比较，仿真结果表明，加入局部搜索后的离散粒子群优化算法具有较好的寻优性能。

关键词：跟踪任务分配，指派问题，粒子编码，离散粒子群优化算法，局部搜索

0　引言

现代战争敌我双方对抗的复杂性，要求指挥中心能够根据战场环境，快速、合理地指派多地面无人平台（Unmanned Ground Vehicle，UGV）协同跟踪多个目标，最大限度地发挥协同跟踪的优势。多平台多目标协同跟踪中的平台指派问题是非常重要的一个环节。多平台多目标协同跟踪问题具有平台规模较大的特点，为尽量降低平台的运动能耗，提高多目标跟踪系统性能，需要将多平台进行合理指派，使它们能够互相协作，协同跟踪各个目标。为此需要构建多平台多目标协同跟踪指派问题数学模型，把多平台多目标协同跟踪指派问题转化为受约束的组合优化问题，然后采用优化算法求解指派问题。

指派给被跟踪目标的平台越多，则平台可获得的关于目标的数据越可靠，从而可得到对该被跟踪目标更优的跟踪性能，在存在多个被跟踪目标情况下，就需要指挥中心合理指派平台跟踪目标。本文将多平台多目标协同跟踪中的平台跟踪任务分配看作一个广义指派问题，即平台数m和目标数n不相等，由指挥中心按照一定的指派原则和约束条件，给多平台指派跟踪任务，指派多个平台跟踪多个目标，使其总作战效果达到最优或较优。当然，本文设计的基于粒子群优化算法的指派方案也适合于平台数m和目标数n相等的情况。

1　多平台多目标指派问题及数学模型

多平台多目标指派问题描述：设有n个目标，现有m（m×n）个UGV，指挥控制中心需指派UGV去协同跟踪各个目标。规则如下：每个平台仅跟踪一个目标（允许多个平台协同跟踪同一个目标），即指挥中心仅分配给每个平台一个跟踪任务，每项跟踪任务可由多个平台协同完成，即指挥中心可分配多个平台跟踪一个目标，且保证各个平台尽量均匀地跟踪各个目标，已知第i个UGV到第j个目标的距离为dij（i=1，2，…，m；j=1，2，…，n），需确定最优指派方案，使得所有UGV与目标的距离之和尽量小。

根据要保证各个平台尽量均匀地跟踪各个目标的规则，假设m=6，n=4时，则指派UGV1、UGV2跟踪目标T1，指派UGV3、UGV4跟踪目标T2，指派UGV5、UGV6分别跟踪目标T3、T4是一种可行的指派方案。而指派UGV1、UGV2、UGV3跟踪目标T1，UGV4、UGV5、UGV6分别跟踪目标T2、T3、T4为不可行的指派方案。假设m=9，n=3时，则指挥控制中心指派3个平台群（每个群由3个UGV组成）各自跟踪不同的目标，这样的规则约束可以使得多个平台较均匀地承担跟踪任务。定义UGV-目标指派矩阵Am×n表示指派方案，其元素为aij（i=1，2，…，m；j=1，2，…，n），aij取值为0或1，aij=1表示指派第i个UGV跟踪第j个目标，否则aij=0。现对上述问题进行建模：

目标函数：

约束条件：

其中［.］表示取整操作。目标函数（1）表示求解最优指派方案使得指派总效益最优（距离和最小）；约束条件（2）表示每个平台仅能跟踪一个目标；约束条件（3）表示指挥中心均匀指派UGV跟踪各个目标，每个平台至少跟踪一个目标；由dij组成的矩阵Dm×n=（dij）m×n为多平台多目标跟踪指派问题的UGV-目标距离矩阵。

从模型可看出，多平台多目标跟踪指派问题属于NP-hard问题，当平台数及目标数较大时，采用精确算法求解将非常耗时，而智能优化算法在求解此类问题时具有较大的优势，典型的智能算法有遗传算法、蚁群算法、粒子群优化算法等。其中粒子群算法与遗传算法、蚁群算法相比，粒子群优化算法的实现更加方便、需设定的参数更少且粒子群优化算法执行速度更快［1］。故本文采用粒子群优化算法解决多平台多目标协同跟踪中的指派问题。

2　离散粒子群优化（DPSO）算法设计

2.1基本粒子群算法

粒子群优化（Particle Swarm Optimization，PSO）算法［2］是一种进化计算技术，由Kennedy和Eberhart提出，源于对鸟群捕食行为的研究。在PSO算法中，优化问题的解被抽象成无质量和体积的粒子，并延伸到多维空间。粒子在多维空间中的位置为一个矢量，各个粒子的飞行速度也是一个矢量。通过各个粒子的相互协作与信息共享，并不断调整粒子的速度和位置，从而使得整个粒子群向最优解收敛。由于PSO算法具有实现简单和收敛速度快等特点，因此，自其提出以后，引起了国内外学者的高度关注，成为群智能研究领域的主要算法之一，实验结果表明粒子群优化算法能够解决遗传算法能够解决的各类优化问题［3］。自粒子群算法提出至今，学者们对其展开了大量研究工作，对PSO算法进行了各种改进，主要有基于惯性加权因子的改进［4］、基于加速度因子的改进［5］、融合其他算法的PSO［6］等。

粒子群优化算法最初用于连续空间的问题优化，其基本粒子群算法的数学描述如下：

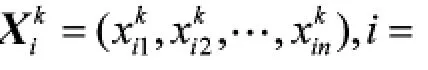
其中，ω是惯性加权因子，c1、c2为加速度因子，rand1和rand2为0~1之间的随机数。vmax为最大速度，用以限制粒子的飞行速度。pbesti为粒子个体极值，记录当前粒子历史最优位置。gbest为全局极值，记录整个群体的历史最优位置。通过式（1）进行速度更新，式（2）进行位置更新，通过迭代，粒子能够不断更新，逐渐“飞”至最优解所在位置。当迭代达到最大次数或搜索结果达到预设阈值时，优化算法结束，最后输出为PSO算法搜索到的最优解。

2.2粒子编码与迭代

粒子群算法主要用于求解连续、无约束的优化问题，在离散、具有约束的优化问题求解方面的应用还比较少，为了将粒子群算法应用于广义指派问题，必须将其离散化，文献［7］采用离散化粒子群算法解决作战弹药分配问题，但不适合求解m和n相差较大的问题。本文采用基于连续空间的PSO算法，对粒子位置进行离散编码，得到指派问题的可行解，采用连续空间PSO算法的速度、位置更新规则，使得算法计算简单、耗时短，较好地解决了多平台多目标跟踪问题中的多平台指派问题，能够得到最优解或较优解。

针对第2节建立的m个UGV，n个目标的多平台多目标指派问题模型，采用长度为m的由1~n组成的自然数串表示粒子位置X：

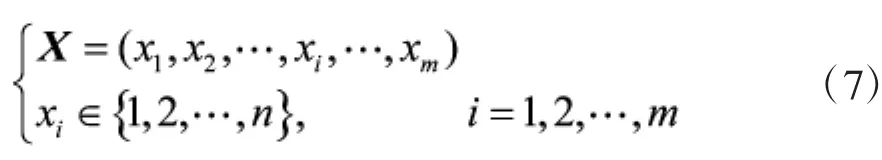
采用式（7）表示的粒子位置是一个m维矢量，是一种指派方案，粒子每一维的数值在1~n的自然数中取，xi=j表示第i维对应的UGV跟踪第j个目标，j=1，2，…，n。但是上述粒子位置并不能保证这是一种可行指派方案，即并不能保证满足约束条件（3），因此，需要对粒子位置更新式（6）产生的连续型位置矢量Xnew进行离散化编码，设计如下编码方案：

Step 1：按Xnew的每一维度的数据进行升序排序，将排序结果存于Xsort，并记录下Xnew和Xsort之间的映射关系。

Step 2：对Xsort数组中索引（Index）为1~［m/n］*n（索引从1开始编号）的数组根据索引对n取模的情况赋值：若Index Mod n≠0，则Xsort=Index Mod n；如果Index Mod n=0，则Xsort=n。若m-［m/n］*n≠0，则对索引为［m/n］*n~m的Xsort数组元素赋互不重复的1~m的随机数。

Step 3：根据Step 1已记录下的排序映射关系进行逆向映射，即可得满足约束条件的X'new的离散化编码。

Step 4：编码后的X'new为一个满足约束条件的可行指派方案，粒子仍按照式（5）、式（6）更新速度和位置更新，对新得到的连续型新矢量Xnew再进行编码得到离散化X'new编码，如此可一直进行迭代求解。

该编码方案建立了粒子位置矢量与可行离散解空间的映射关系，编码后的粒子由于已将不可行解排除之外，因此，搜索范围被大大压缩，搜索效率显著提高。图1为粒子离散化可行编码生成示例。

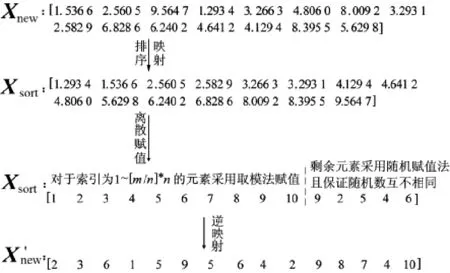
图1粒子离散化可行编码生成示例

2.3粒子适应度计算

根据目标函数式（1），按式（8）选取粒子的适应度值：

经过上述粒子速度、位置表示、编码、适应度计算等定义之后，就基本完成了改进的离散粒子群优化（IDPSO）算法的设计，为了使得IDPSO能够获得更好优化效果，需加入2.4小节的局部搜索。

2.4加入局部搜索

为增加算法的寻优能力，在算法中增加局部搜索操作。本文在得到一次粒子离散编码后，计算其适应度值之后，还要基于贪婪思想对当前离散编码的所有邻域作局部搜索。

定义：矢量P的邻域：所有交换两个不同索引位置对应值而得到的新矢量的集合称为P的邻域。

局部搜索过程如下：

Step 1：对离散编码X'new产生两个不同位置的索引，交换两处索引位置上的值，得到一个新的离散编码。

Step 2：计算新的离散编码对应的适应度值，若该适应度值优于当前粒子适应度值，则记录下该离散编码及适应度值。

Step 3：遍历离散编码X'new的邻域，若遍历完则转Step 4；否则转Step 1。

Step 4：结束局部搜索，若离散编码邻域的适应度值优于X'new对应的适应度值，则用该离散编码对应的连续粒子位置更新粒子，否则仍用当前连续粒子位置作下一次迭代。

3　仿真实验和结果分析

仿真实验在安装有Matlab 2010b编程环境的PC上进行，PC机配置为Windows 7 Home操作系统，Intel（R）Core（TM）i3-2310 CPU@2.10 GHz，4 G内存，500 G硬盘。假设在［0，5 000］m×［0，5 000］m的监测区域内存在3个目标，指挥控制中心及平台可通过携带的传感器获得目标及自身的位置信息，监测区域内有9个可用UGV及若干备用UGV，9个可用UGV及3个目标的分布图如图2所示。算法参数：ω采用随迭代次数不断线性下降的方式取值，取值范围为（0.4，0.9）。c1=1.494 45，c2=1.494 45。

图2多平台多目标分布图

UGV-目标距离矩阵如下所示：

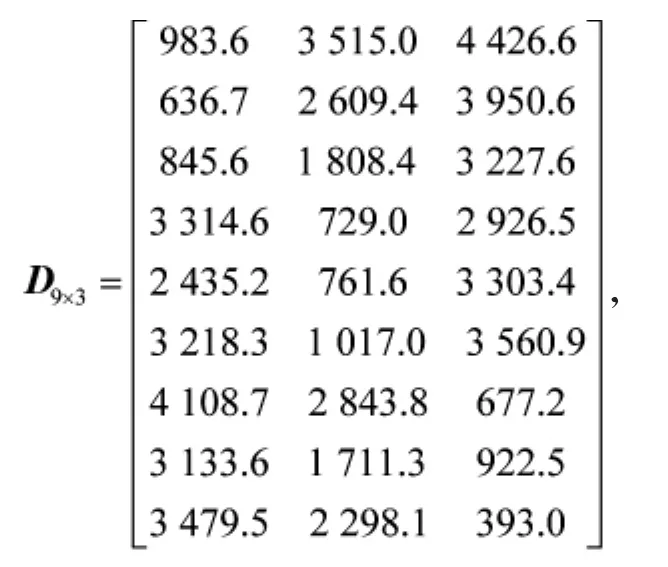
得到的最优指派矩阵A9×3如下所示：

若算法不加入局部搜索，则不能保证每次都得到最优解，而运行加入局部搜索的算法，种群规模Size为10，最大迭代次数为50，算法运行100次，每次均能得到最优解，即适应度值Fitness=6 966.2，所以在算法中加入局部搜索很有必要。

4　结论

针对多平台多目标跟踪中的UGV多于被跟踪目标的指派问题，本文提出了一种改进的离散粒子群优化算法，为增加算法的寻优能力，在算法中增加局部搜索操作，通过与未加入局部搜索的离散粒子群优化算法在仿真实验中的比较，表明本文所提出算法在性能优化方面的有效性。

参考文献：

［1］陈翔，顾庆，王子元，等.一种基于粒子群优化的成对组合测试算法框架［J］.软件学报，2011，22（12）：2879-2893.

［2］KENNEDY J，EBERHART RC. Particle swarm optimization ［J］. In：Proc. of the IEEE Conf，on Neural Networks，Perth：IEEE Press，1995（4）：1942-1948.

［3］HASSAN R，COHANIM B，DE WECK O，et al. A comparison of particle swarm optimization and the genetic algorithm［C］//Proceedings of the 1st AIAA Multidisciplinary Design Optimization Specialist Conference，2005.

［4］EBERHART R C，SHI Y. Comparing inertia weights and constriction factors in particle swarm optimization［C］//Evolutionary Computation，2000，Proceedings of the 2000 Congress on. IEEE，2000.

［5］GUO W，CHEN G，FENG X. A new strategy of acceleration coefficients for particle swarm optimization［C］//Computer Supported Cooperative Work in Design，2006，CSCWD'06. 10th International Conference on，IEEE，2006.

［6］高鹰，谢胜利.免疫粒子群优化算法［J］.计算机工程与应用，2004，40（6）：4-6.

［7］赵志宁，石全，张军刚.基于改进离散粒子群优化算法的作战弹药分配研究［J］.数值计算与计算机应用，2013，34（3）：205-211.

Research on Assignment Problem for Coordinated Tracking of Multi- platform Multi- target

SONG Zhi-qiang1，2，ZHOU Xian-zhong1，XU Feng3
（1. School of Management and Engineering，Nanjing University，Nanjing 210093，China；
2. Institute of Electrical and Information Technology，Suzhou Institute of Trade & Commerce，Suzhou 215009，China；3. North Automatic Control Technology Institute，Taiyuan 030006，China）

Abstract：Aiming at the characteristics of requiring multiple unmanned ground vehicles tracking multiple targets as evenly as possible in the coordinated tracking system of multi-platform multi-target，an improved discrete particle swarm optimization algorithm is proposed. Firstly，the iterative formula of speed and position of the particle swarm optimization algorithm in the continuous space are adopted，and then a discrete particle coding scheme is designed to the particle position，making the particle coding corresponding to the feasible assignment solution; Secondly，a local search is introduced，providing better optimization performance. Finally，the proposed algorithm is applied to the assignment problem of coordinated tracking for the multi-platform multi-target，and compared with particle swarm optimization algorithm without the local search. The simulation results show that the discrete particle swarm optimization algorithm with a local search has better optimization performance.

Key words：tracking task allocation，assignment problem，particle coding，discrete particle swarm optimization algorithm，local search

作者简介：宋志强（1977-），男，江苏张家港人，副教授，博士研究生。研究方向：网络化群智能系统的协调与控制。

*基金项目：国家自然科学基金（71171107）；装备预研基金重点项目（9140A06050213BQX）

收稿日期：2015-01-12修回日期：2015-03-17

文章编号：1002-0640（2016）02-0032-04

中图分类号：O22

文献标识码：A