农业节水灌溉项目优选—基于改进模糊物元分析模型
2016-03-23宁宝权陕振沛
宁宝权,陕振沛
(1.六盘水师范学院 数学系,贵州 六盘水 553004;2.大连理工大学 管理与经济学部,辽宁 大连 116024)
农业节水灌溉项目优选
—基于改进模糊物元分析模型
宁宝权1,2,陕振沛1
(1.六盘水师范学院 数学系,贵州 六盘水553004;2.大连理工大学 管理与经济学部,辽宁 大连116024)
摘要:借助改进熵权法对评价指标进行赋权,在灰关联分析和模糊物元分析理论的基础上,建立了改进熵和灰关联分析的模糊物元分析模型。根据灰色关联度的大小对评价对象进行排序,并将其应用到农业节水灌溉项目的优选中,说明此模型的合理性。
关键词:农业节水灌溉项目;改进熵权法;灰关联分析;模糊物元分析;灰色关联度
0引言
我国农业节水灌溉项目关系到农民增收问题,而且影响因素较多,是一个多属性决策问题。因此,如何运用合理、科学的评价方法对农业节水灌溉项目进行综合评价是个非常值得研究的问题。孙士尉、张铁壁、王海松等将模糊控制算法应用在滴灌节水系统中,实践表明该算法有效[1];曹然、王会英、郭微建立了基于熵理论和遗传算法的优化模型,通过实例试验提出的模型用于作物灌溉决策优化,比基本遗传算法计算精度有了明显提高[2];陈娟、李杰将组合权的灰色关联理想模型应用到节水灌溉项目中的综合评价中,并取得了良好的效果[3];黄娅婷将熵值理论与模糊物元建模相结合,建立了节水灌溉项目的熵权的模糊物元节水灌溉项目综合评价模型,结果表明模型简单可行、方便实用[4]。本文对传统的熵权法进行了改进,克服其弊端,扩展其使用范围,对指标进行赋权,在模糊物元分析理论的基础上,结合灰关联分析,建立了改进熵和灰关联分析的模糊物元分析模型。该模型综合了熵权法、灰关联分析和模糊物元分析的诸多优点,将该模型应用到农业节水灌溉项目的优选中,根据灰色关联度的大小对农业节水灌溉项目进行排序,从而得到最优的农业节水灌溉项目。
1模糊物元分析
1.1构造复合模糊物元

(1)
其中,Mi为比较事物(评价对象);Cj为比较事物的特征(评价指标);vij为Cj相对应的量值,i为比较事物的序号;j为比较事物特征的序号。
1.2将复合模糊物元矩阵转换为隶属度矩阵
模糊物元矩阵转变为隶属度矩阵,要求引入从优原则。根据本文的指标的类型,指标分成正向指标、负向指标和适中型指标3类,则指标隶属度的计算也分成3类;通过计算指标的隶属度,可以把复合模糊物元矩阵转换为指标的隶属度矩阵。
1)正向指标隶属度计算。正向指标是指数值越大越好的指标。设xij为第i个评价对象第j个指标的隶属度,vij为第i个评价对象第j个指标的值,m为被评价对象的个数。根据正向指标的标准化公式[7],则xij为
(2)
2)负向指标隶属度计算。负向指标是指数值越小越好的指标。根据负向指标的标准化公式[7],则xij为
(3)
其中,式(3)中各个符号的含义与式(2)相同。
3)适中型指标隶属度计算。适中型指标是指数值既不太大也不太小的指标,取中间值。根据适中型指标的标准化公式[7],则xij为
(4)
其中,vj为指标的适中值。式(4)中各个符号的含义与式(2)相同。

(5)
1.3构造最优模糊物元
根据式(5)的隶属度矩阵,可以构造最优评价对象M0的模糊物元R0n。根据本文的隶属度计算方式,无论原始指标是正向指标还是负向指标,标准化后的指标都是正向指标,所以只需要取指标隶属度的最大值。最优模糊物元为
(6)
1.4改进熵权法确定指标权重

1)各指标熵值确定方法。
(7)

2)各指标差异系数确定方法。
Hj=1-Pj
(8)
3)权重确定方法。对指标差异系数作标准化处理,可以得到权重。计算公式为
(9)
1.5构造改进熵和灰关联分析的模糊物元分析模型
灰色系统中的灰色关联分析[9-10]由于其使用方便、容易操作,因而在综合评价中经常使用灰色关联度体现两列数据间的误差程度。本文在原始灰色关联分析的基础上引入指标的组合权重,并结合模糊物元分析理论,得到改进熵和会关联分析的模糊物元分析模型。具体计算步骤如下:
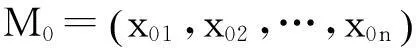
2)计算灰色关联系数。灰色关联系数按照以下公式进行计算。
(10)
其中,i为第i个评价对象;k为第k个最优指标;β为表示分辨系数,0<β<1,通常取β=0.5。
3)计算灰色关联度。计算每个评价对象的每个模糊物元序列和最优模糊物元序列的组合加权灰色关联度,按照以下公式进行计算,即
(11)
2应用实例
2.1构造复合模糊物元

(12)
2.2将复合模糊物元矩阵转换为隶属度矩阵

(13)
2.3构造最优模糊物元
根据式(13)的复合模糊物元隶属度矩阵,取式(13)中每一个指标(也就是每一列指标隶属度)的最大值,显然每一列的最大值都是1,则最优模糊物元公式为
(14)
2.4改进熵权法确定指标权重
以式(13)的隶属度矩阵中的数据为基础,根据文中的式(7)~式(9),可以得到15个评价指标的熵权法权重,如表1所示。
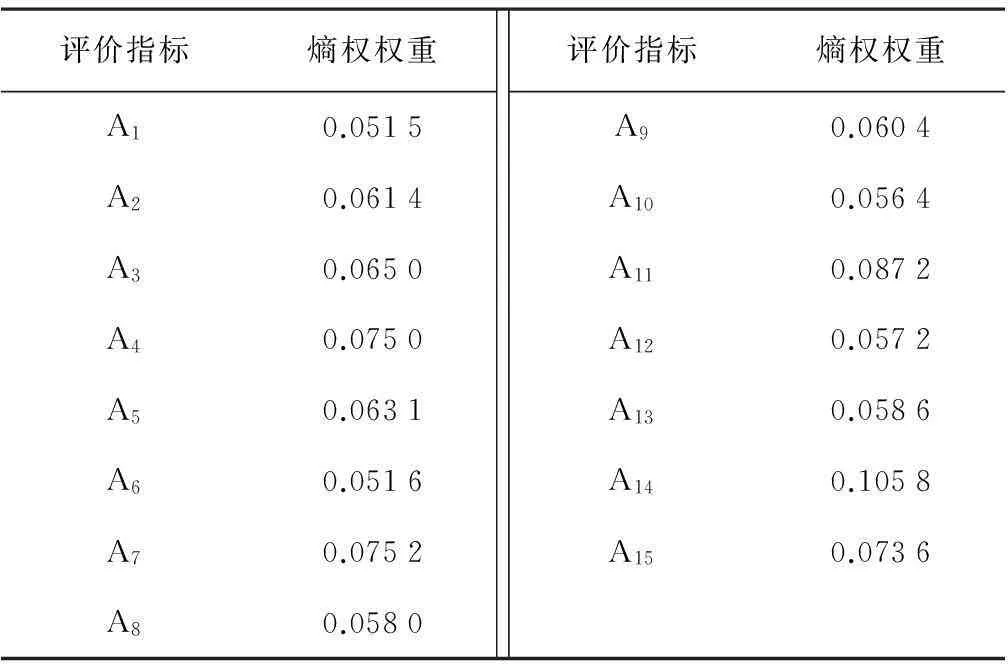
表 1 评价指标的权重
2.5灰色关联度计算
结合式(13)和式(14)中的数据,根据文中式(10)和式(11)可以计算每一个备选县的灰色关联度。同时,根据灰色关联度的大小能够得到6个备选县的排序,如表2所示。

表2 评价对象的灰色关联度及排序
根据表2中的排序结果,6个备选县的排序为P1≻P3≻P6≻P4≻P2≻P5(Ai≻Aj表示Pi优于Pj)。根据排序结果,很显然应该选择P1和P3。所得的结果和文献[3]的结果是一样的,说明此模型是有效的。
3结论
本文在传统的熵权法的基础上,对其进行改进,使其应用范围更广、更实用。同时,并运用改进熵权法对指标进行赋权,在物元分析理论的框架下,结合灰色关联理论,构建了基于改进熵和灰关联分析的模糊物元分析模型。将该模型应用到农业节水灌溉项目的综合评价中,根据排序结果给出农业节水灌溉项目排序,说明了模型的有效性,同时丰富了指标赋权方法和农业节水灌溉项目的评价方法。此模型不仅能够应用到农业节水灌溉项目综合评价中,还可以运用到其它相似的综合评价问题上,值得借鉴和推广。
参考文献:
[1]孙士尉,张铁壁,王海松,等.模糊控制算法在滴灌节水系统中的实现[J].农机化研究,2010,32(6):66-66.
[1]曹然,王会英,郭微.基于熵理论和遗传算法的作物灌溉决策的优化研究[J].农机化研究,2011,33(9):89-92.
[2]陈娟,李杰.基于组合权的灰色关联理想模型在节水灌溉项目中的应用[J].人民珠江,2010(2):27-29.
[3]黄娅婷.基于熵权模糊物元模型的节水灌溉工程优选[J].广东水利水电,2011(4):9-11,21.
[4]傅金祥,刘聪慧,张荣新,等.欧氏贴近度模糊物元分析法优选制浆造纸中段水处理工艺[J].环境工程学报,2014,8(11):4600-4604.
[5]王春娟,冯利华.物元分析在需水量变化预测中的应用[J].浙江师范大学学报:自然科学版,2013,36(3):355-360.
[6]郭亚军.综合评价理论、方法及应用[M]北京:科学出版社,2007:49-51.
[7]程启月.评测指标权重确定的结构熵权法[J].系统工程理论与实践,2010,30(7):1225-1228.
[8]曹辉.基于熵权灰色关联模型的陕西省可持续发展能力探究[J].科技进步与对策,2014,31(9):51-55.
[9]王霞,党耀国,谈静艳.基于灰关联熵的多指标灰靶决策方法[J].数学的实践与认识,2014,44(24):54-58.
[10]凌春雨,张得志,李双艳.改进灰色关联分析法在物流园区选址中的应用[J].现代物流,2005,27(4):20-23.
Optimal Selection of Agricultural Water Saving Irrigation Projects—Based on Improved Fuzzy Matter-element Analysis Model
Ning Baoquan1,2, Shan Zhenpei1
(1.Department of Mathematics, Liupanshui Normal University, Liupanshui 553004,China;2.Faculty of Management and Economics,Dalian University of Technology,Dalian 116024,China)
Abstract:Evaluation indexes were weighted by improved entropy weight method,fuzzy matter-element analysis model based on improved entropy and grey relational analysis on the basis of fuzzy matter-element analysis and grey relational analysis was builded,evaluation objects are ranked by sizes of grey relational degree and applied the model to optimal selection of agricultural water saving irrigation projects,the case proved the model effective.
Key words:agricultural water saving irrigation projects; improved entropy weight method;grey relational analysis;fuzzy matter-element analysis; grey relational degree
文章编号:1003-188X(2016)04-0049-04
中图分类号:N945.1;S277
文献标识码:A
作者简介:宁宝权(1980-),男,黑龙江绥化人,副教授,博士研究生,(E-mail)bqning@126.com。
基金项目:贵州省科学技术基金项目(黔科合J字LKLS[2013]33号);贵州省教育厅高校人文社会科学研究项目(13QN011);贵州省教育厅自然科学基金项目(黔教科2010101);六盘水师范学院自然科学研究项目(LPSSY201313);六盘水师范学院数学教育教学团队项目(LPSSYjxtd201102)
收稿日期:2015-03-15
