曲柄滑块式清选筛机构惯性力平衡研究

李　革，王　婵，李颖聪，方明辉

(1.浙江理工大学 机械与自动控制学院，杭州　310018；2.湖州思达机械制造有限公司，浙江 湖州　313000；3.湖州师范学院，浙江 湖州　313000)



曲柄滑块式清选筛机构惯性力平衡研究

李革1，王婵1，李颖聪2，方明辉3

(1.浙江理工大学 机械与自动控制学院，杭州310018；2.湖州思达机械制造有限公司，浙江 湖州313000；3.湖州师范学院，浙江 湖州313000)

摘要：利用解析法对曲柄滑块式清选筛机构进行运动学及动力学分析，得到构件的惯性力和机构的总惯性力，通过质量代换法对该机构进行平衡建模，计算出机构部分平衡时曲柄上添加的平衡质量，并进行平衡质量的优化分析。在履带式谷物联合收割机上进行曲柄滑块式清选筛机构的振动试验，获取机架上不同点及驾驶室内的振动信号，采用时域平均法对振动数据进行处理，以验证理论分析正确性。理论分析及试验研究表明：曲柄滑块式清选筛进行部分平衡时，安装在曲柄链轮上的平衡块在矢径r1=95mm、质量为2kg时机器振动达到最小。

关键词：联合收割机；曲柄滑块式清选筛；惯性力

0引言

清选筛是联合收割机的重要部件之一，其作用是实现物料与茎秆、颖壳、杂草等杂物之间的分离[1]。大多数联合收割机采用曲柄摇杆式清选筛机构，对该机构振动的研究主要是进行惯性力平衡分析及运动仿真。近些年，我国的一些履带式谷物联合收割机借鉴国外的技术，开始应用曲柄滑块式清选筛机构，以解决清选筛运动机构安装空间有限的问题，并可以达到简化结构的目的。但是，由于缺乏针对曲柄滑块式清选筛机构振动的理论研究，我国的一些谷物联合收割机的曲柄滑块式清选筛机构惯性力平衡量基本是凭经验选取，造成了平衡量设计不合理、机器振动过大、工作可靠性降低等问题。为此，本文就曲柄滑块式清选筛的结构进行了惯性力平衡研究，提出了该机构惯性力平衡的优化方法。

1工作原理及惯性力分析

1.1　曲柄滑块式清选筛工作原理

将清选筛结构简化为一个具有两个滑块的曲柄滑块机构(见图1)，由曲柄(偏心轮)、连杆、筛面、滑块1、滑块2、机架及曲柄链轮组成。其中，曲柄与曲柄链轮为同轴固定连接，导轨固定于机架上。

1.偏心轮　2.连杆　3.清选筛　4.滑块1

1.2　滑块式清选筛运动学及惯性力分析

机构的运动分析有多种方法，常用的为图解法和解析法。图解法是利用理论力学中的运动合成原理，对机构进行速度和加速度的矢量合成[2]；解析法则是对机构进行运动学建模，借助计算机分析运动过程中的参数特性并绘制参数曲线图[3]，便于对机构进行优化。本文采用解析法，建立位移方程式，进行一次、二次求导，得到机构的运动速度及加速度。以曲柄回转中心O为原点建立坐标系XOY。一般履带式谷物联合收割机的曲柄滑块式清选筛机构中各杆长度及质量分别为：L1=LOA=16mm、L2=LAB=59mm、L3=LBC=1 124mm、m1=1kg、m2=1kg、m3=70kg。其中，LOO1表示曲柄OA的质心O1与O点的距离、LAO2表示AB的质心O2与A点的距离，LBO3表示筛面质心O3与B点的距离。同时有：LOO1=s1=L1/2、LAO2=s2=L2/2,质心O3的相对位置为θ=6.53°、LBO3=s3=534mm，θ表示BO3连线与筛面BC的夹角，两滑块的运动方向线与水平面的夹角为β=30°；右侧滑块1的运动方向线与X轴的交点距原点O的距离l1=30mm，左侧滑块2的运动方向线与X轴的交点距原点O的距离l2=1 300mm；同轴固定连接的曲柄链轮与曲柄沿轴线方向的距离为h=200mm，平衡块与偏心轮在同一平面内；曲柄以w匀速转动。机构的运动学模型为

式中A、B—铰链点A、B的位移矢量；

VA、VB—铰链点A、B的速度矢量；

aA、aB—铰链点A、B的加速度矢量；

xA、xB—铰链点A、B的水平位移；

yA、yB—铰链点A、B的竖直位移；

VxA、VxB—铰链点A、B的水平速度；

VyA、VyB—铰链点A、B的竖直速度；

axA、axB—铰链点A、B的水平加速度；

ayA、ayB—铰链点A、B的水平加速度；

α1—曲柄转角；

α2—连杆AB与水平面夹角。

由于本文中的筛面做平移运动，根据理论力学刚体平移定理[4]可知：铰链点C的运动参数与铰链点B的运动参数是相同的。同理，清选筛质心的运动学参数也与铰链点B运动参数一样，所以不再对其进行建模分析。

α2的计算过程为

同理得

式中α3—筛面BC与水平面的夹角。

机构中各构件质心运动模型为

式中OO1、OO2、OO3—质心O1、O2、O3的位移矢量；

VO1、VO2、VO3—质心O1、O2、O3的位移矢量；

aO1、aO2、aO3—质心O1、O2、O3的加速度矢量；

S1、S2、S3—质心O1、O2、O3的质心半径。

惯性力的方向与加速度方向相反，计算时需要改变其数学符号,得到各构件的惯性力为

式中IO1、IO2、IO3—曲柄OA、连杆AB、筛面BC的惯性力矢量。

平衡前曲柄滑块式清选筛机构的总惯性力矢量为各构件惯性力矢量之和，则有

I=IO1+IO2+IO3

式中I—平衡前机构总惯性力矢量；

I—平衡前机构总惯性力标量；

Ix—平衡前机构总惯性力水平分量；

Iy—平衡前机构总惯性力竖直分量。

运用MatLab软件对上述机构的运动学和动力学模型进行运动仿真，得如图2所示的曲柄滑块式清选筛总惯性力标量及水平竖直分量曲线图。

2机构惯性力的部分平衡

2.1　惯性力平衡模型分析

目前，有两类方法可建立运动机构的惯性力平衡模型，即线性无关矢量法和质量代换法。其中，线性无关矢量法计算过程比较复杂，本文采用质量代换法建立惯性力平衡模型。为使构件在质量代换前后构件的惯性力和惯性力偶矩保持不变，应满足下列3个条件[2]：①代换前后构件质量不变；②代换前后构件的质心位置不变；③代换前后构件对质心轴的转动惯量不变。

在本机构中，清选筛的运动为平动，所以可采用静代换的方法进行质量代换，只需满足前两个条件。如图1所示的曲柄滑块清选筛，其运动形式为刚体的平动，故筛面上的质心位置不影响机构的惯性力大小，本文中按其在构件中心处考虑。构件1、2、3的质量分别为m1、m2、m3，并将各构件的质量通过静代换方法得各铰链点上的集中质量为

式中m1O、m1A—构件1在铰链点O、A处的集中质量；

m2A、m2B—构件2在铰链点A、B处的集中质量；

m3B、m3C—构件3在铰链点B、C处的集中质量。

所以，铰链A、B两点处的集中质量为

mA=m1A+m2A

mB=m2B+m3B

式中mA—铰链点A处的集中质量；

mB—铰链点B处的集中质量；

mC—铰链点C处的集中质量。

在铰链A处，集中质量mA产生的惯性力，可在曲柄OA的反向延长线上添加平衡质量m，使之满足

式中r—平衡质量矢径，r=L1。

在铰链B处，集中质量mB产生的为往复惯性力IB，其大小随曲柄转角的变化而变化，且与该点的加速度大小相关，则有

IB=mB×aB=mB×[axB,ayB]T

式中IB—平衡质量惯性力矢量。

式中mb—矢径为r时添加的平衡质量；

r1—平衡质量矢径；

mb1—矢径为r1时添加的平衡质量；

Imbx—平衡质量水平惯性力；

Imby—平衡质量水平惯性力。

在对机构铰链点A、B、C等3点处的集中质量进行惯性力的完全平衡时，曲柄处的平衡块质量会很大，而且安装位置有限。本文中只考虑A、B铰链点处部分的惯性力平衡。

从图1可以看出：河道两侧的两块绿地分别被划分为多个不规则小三角形块。小三角形块的划分是由指定区域的形状规则程度所决定。整体计算边界为规则的矩形时，三角网呈现出比较一致的小三角形块；而计算边界形状极为不规则时，三角网则由差异较大的不同形状、不同大小三角形组成。

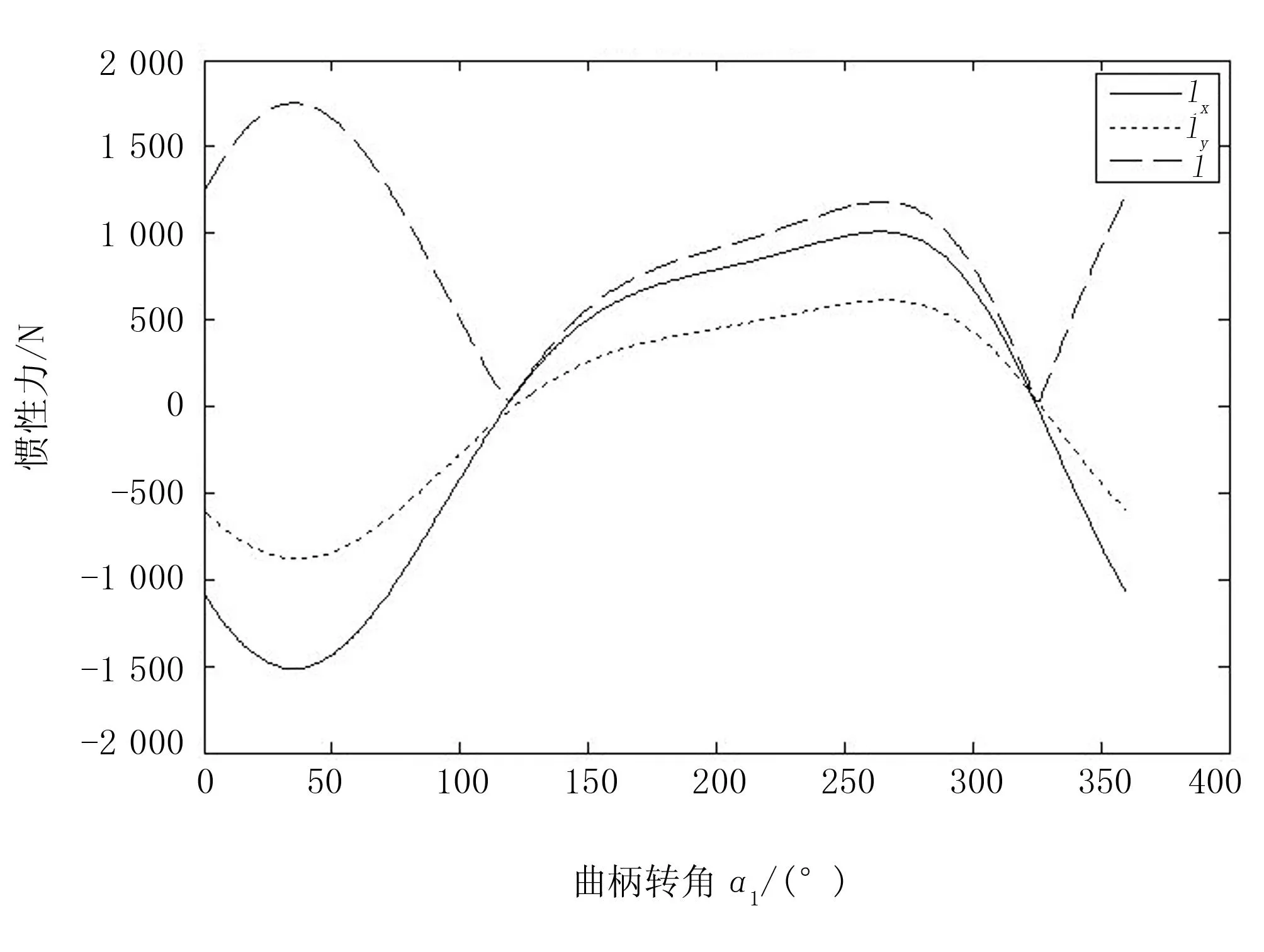
图2　平衡前惯性力曲线图

2.2　平衡质量优化

对机构进行平衡时，以平衡后水平、竖直以及总惯性力的最大值最小并且平均值为最小作为优化目标进行优化。部分平衡后机构惯性力为

式中I2—部分平衡后的机构总惯性力。

基于MatLab软件对机构平衡前与平衡后惯性力进行对比仿真分析，编辑main函数，在矢径为r=L1=16mm时，平衡质量mb在[0,40]之间以步长0.5kg取值计算，求得不同平衡质量mb2下惯性力水平、竖直以及总惯性的最大值和平均值，分别表示为maxIx、maxIy、maxI、averIx、averIy及averI。绘制变化曲线如图3所示。

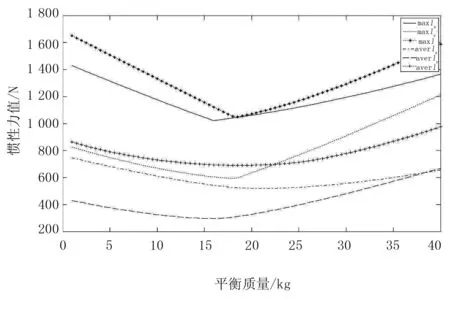
图3　矢径r=16mm时平衡后惯性力曲线图

由图3可以看出：矢径r=L1=16mm、曲柄上的平衡质量在15～25kg之间时，整个机构的惯性力较小；而当平衡质量继续增加时，机构的惯性力又继续增大。由此可见，矢径为r时的较优平衡质量在15～25kg之间。显然，这么大的平衡质量不合适，所以可通过增加平衡质量矢径的方法来减轻质量。又因为受安装空间限制，在曲柄处增加平衡质量矢径不可能。所以，把平衡质量转移到与曲柄同轴固定连接的曲柄链轮上(两者之间的距离200mm)，这时平衡质量矢径的长度可达95mm，即取r1=95mm。

在矢径r1=95mm时，使mb1在 [0,4]kg之间以步长为0.5kg取值计算，求得不同平衡质量mb1下惯性力水平竖直方向及总惯性的最大值和平均值，表示为maxI1x、maxI1y、maxI1、averI1x、averI1y及averI1。绘制变化曲线如图4所示。

由图4可以看出：矢径r1=95mm、曲柄上的平衡质量小于2kg时，随着平衡质量的增加，机构的惯性力逐渐减小；而平衡质量大于2.5kg后，随着平衡质量的增加，机构惯性力越来越大。考虑到清选筛机构质量已经很大，所以选取矢径为r1时的平衡质量进行机构惯性力平衡，此时机构的较优平衡质量在2～2.5kg之间。

平衡质量分别为2、2.5kg及未添加平衡质量的惯性力曲线如图5所示。其中，Ix2、Iy2,I2分别表示在2kg平衡质量下的水平、竖直及总惯性力；Ix2.5、Iy2.5、I2.5分别表示在2.5kg平衡质量下的水平、竖直及总惯性力；Ix、Iy、I分别表示在无平衡质量下的水平、竖直及总惯性力。

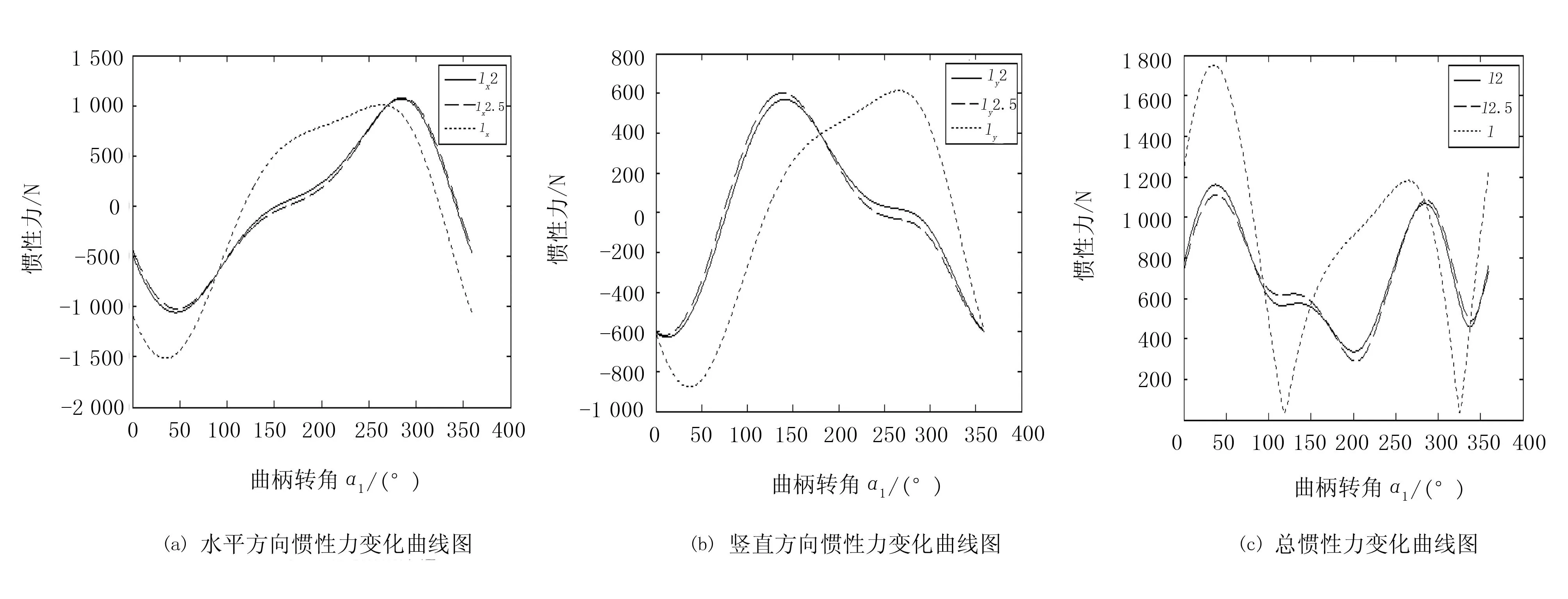
图5　不同平衡质量下的惯性力曲线图

3曲柄滑块式清选筛机构的振动试验

为了验证上述理论的正确性，本文采用振动测试仪对该机构进行了振动试验。

3.1　试验设备

利用AVANT 数据采集与信号分析仪来获取振幅大小的数据。该系统提供了振动和噪声分析领域的专业解决方案，能提供实时信号分析、冲击测量分析、模态数据采集、声压分析及其他应用。分析仪负责采集数据和实时分析，所有的实时分析均由DSP处理器完成，包括信号采集、抽取、滤波、实时分析及信号源输出等；然后，数据通过USB电缆连接，传输到计算机；计算机基于Windows应用软件则主要完成用户测试设置、命令操作、信号及数据的显示和存储等工作。

3.2　试验测试

履带式谷物联合收割机的振源较为复杂，主要包括行走路面不平整、割台、滚筒、发动机及清选筛[5]。所以，本次试验在谷物联合收割机处于停止状态、割台和滚筒均不工作，以及发动机以额定功率输出的工况下进行。试验的测试点1选在振动影响最大的曲柄链轮轴承座附近；测试点2和3选在车架上，以观察对车架振动的影响；测试点4选在驾驶座附近，以观察对驾驶员振动的影响，如图6(a)所示。叠加的平衡块如图6(b)所示，旨在方便测试不同平衡质量下的机构振动。平衡块的安装平面位于曲柄链轮平面上，通过螺栓进行固定，如图6(c)所示。

1.测试点4　2.测试点3　3.平衡块安装位置　4.测试点2　5.测试点1

试验时，以平衡质量在 [0,3]kg之间，步长为0.5kg进行配重的添加，试验测试时间为40s。

在试验过程中，计算机进行数据采集，并通过软件进行离线分析。针对获取的振动数据中混有噪声干扰，本文采用时域平均法对振动信号进行处理，消除无关信号，提高信噪比[6]，从而得到如图7所示的振幅信号。

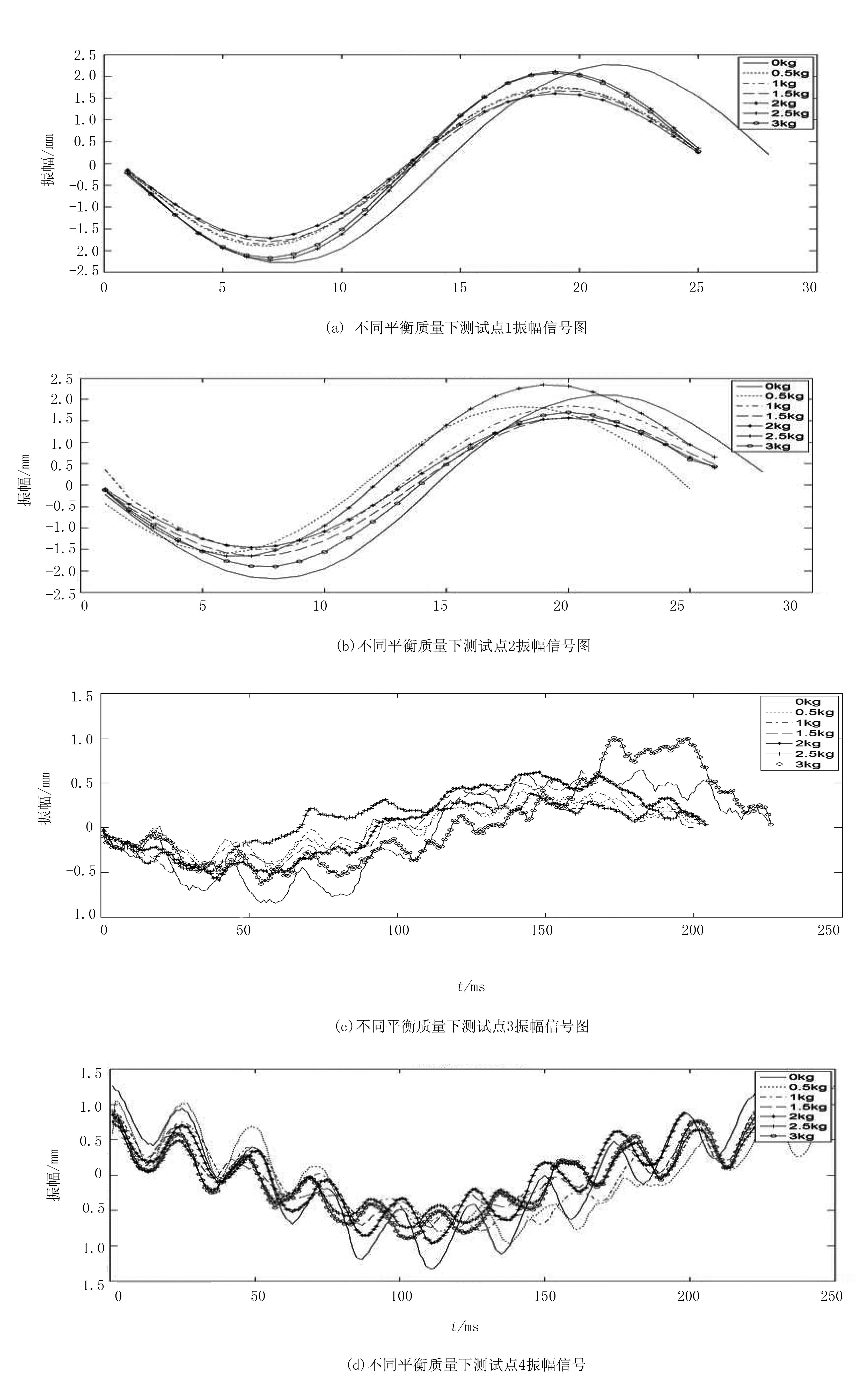
图7　各测试点振幅信号图分析

从图7(a)、(b)中可以看出：测试点1、2在无配重情况下振幅达到最大；当链轮上平衡质量由小到大逐渐增加时，这两个测试点的振幅也随之减小；当平衡质量mb1=2kg时，振幅达到最小；当平衡质量大于2kg时，它们的振幅又随之增大。

测试点3、4的振幅图分别如图7(c)、(d)所示。在平衡质量mb1=1.5～2.5kg之间时，振动比无配重时明显减少，且受到发动机的振动的影响，振源复杂。

综合分析4个不同测试点的振幅信号图，取曲柄链轮上平衡质量2kg为曲柄滑块式清选筛部分平衡时的最优平衡质量。添加2kg的平衡质量后振幅的减小量如表1所示(取绝对值之后计算)。

表1　振动试验结果

4结论

1) 建立了曲柄滑块式清选筛机构的运动学及动力学模型，得到清选筛机构的总惯性力，并通过质量代换法对惯性力进行平衡建模。运用MatLab软件，对机构添加平衡质量前、后的惯性力进行了运动仿真分析。

2) 在清选筛机构曲柄上添加矢径为r=L1=16mm的平衡质量时，机构较优的平衡质量在15～5kg之间；矢径r1=95mm时，机构的较优平衡质量在2～2.5kg之间。鉴于机构质量已经很大，且曲柄滑块式清选筛曲柄上没有安装位置，所以本文选择矢径为r1=95mm时平衡质量对机构惯性力进行部分平衡，并将平衡块安装在与曲柄同轴固定连接距离为h=200mm的曲柄链轮上。

3) 在理论分析和优化的基础上，对安装有曲柄滑块式清选筛的履带式谷物联合收割机进行清选筛的振动试验，将采集数据通过时域平均法分析。结果表明：在平衡质量为2kg时测试点1、2的振幅峰值达到最小，且测试点3、4的振幅峰值相对无配重时也有较大幅度降低，峰值减小量最少21.2%，最多29.5%。通过理论分析和试验，建议曲柄滑块式清选筛的曲柄链轮上平衡质量安装矢径为r1=95mm、质量为2kg，与曲柄方向成180°夹角。

参考文献：

[1]王茜，罗康，杨捷，等.联合收割机振动筛机构惯性力平衡的研究[J].机械研究与应用，2012(6):36-39.

[2]孙恒，陈作模，葛文杰.机械原理[M].北京:高等教育出版社,2006:77-86.

[3]赵匀.农业机械分析与综合[M].北京：机械工业出版社，2008: 86-90.

[4]李耀明，邓玲黎，丁为民.小型联合收割机清选装置的技术分析[J].农机化研究，2004(5):55-56.

[5]洪美琴.联合收割机脱粒系统中振动筛的动力学分析[J].农机化研究，2012,34(5):79-82.

[6]李磊，柴民杰，张英荣.复数矢量法在机构运动和仿真分析中的应用[J]. 邢台职业技术学院学报，2009，26(5)：79-81.

[7]赵环帅，鲍玉新，陈思元，等.国内外高频振动筛技术与设备现状及发展趋势[J].矿山机械，2011,39(10):83-88.

[8]余雷.曲柄滑块机构惯性力优化平衡[J].安徽机电学院学报，1999,14(1):64-67.

[9]陈坤昌，赵匀，俞高红.全喂入式水稻联合收割机切割机构的动力学分析与惯性力平衡[J].机械设计与研究，2005,21(3):98-100.

[10]岳宏伟，杨光， 冯迎春.平面机构惯性力部分平衡最佳平衡量的选取[J].机械工程与自动化，2004(6):18-22.

[11]刘黎阳.平衡曲柄滑块机构的惯性力研究[J].现代制造技术与装备，2008(1):6-8.

[12]黄麟，张春林，韩宝玲.曲柄滑块机构惯性力部分平衡的研究[J].机械设计，2006,23(8):37-40.

[13]何正嘉，刘雄，屈梁生.信号时域平均原理和应用[J].信号处理，1986,2(4):236-243.

[14]孙美玲，朱春吉，岳晓峰.时域同步平均在振动信号分析中的应用[J].长春工业大学学报，2014，35(4)：398-401.

[15]万德安，孙继东，赵永杰.汽车变速箱故障诊断中的时域同步阶次分析法的分析研究[J].计算机测量与控制，2006，14(3)：299-300.

[16]郭瑞琴，孔宪文.平面连杆机构摆动力完全平衡的质量矩替代法[J].机械传动2000，14(1)：9-12.

Abstract ID:1003-188X(2016)08-0024-EA

Investigation on Inertial Force Balancing of Slider-crank Type Cleaning Sieve

Li Ge1, Wang Chan1, Li Yingcong2, Fang Minghui3

(1.College of Machinery and Automation,Zhejiang Sci-Tech University,Hangzhou 310018,China;2.Huzhou starmachine manufacturing Co.LTD.,Huzhou 313000, China;3.Huzhou Universtiy,Huzhou 313000, China)

Abstract：Kinematics and dynamics analysis of the mechanism by analytical method in this paper, obtained the total inertia force of each part and the whole mechanism, analyzed by quality substitution method to built balance model, calculated the part balance quality of the crank and further to optimized. Designed vibration test for the union harvester which has the slider-crank type cleaning sieve, got vibration signal from the point in frame and the cab, vibration signals were processed by time domain average method which proved the correctness of theory analysis. Theoretical analysis and experimental study show that the slider-crank type cleaning sieve part balance quality which installed in the sprocket-crank equal to 2kg, radius vector was 95mm, at this time ,the mechanism has the minimum vibration and achieved the best state.

Key words：union harvest；slider-crank type cleaning sieve； inertial force

中图分类号：S225.3；S220.3

文献标识码：A

文章编号：1003-188X(2016)08-0024-07

作者简介：李革(1957-),男，杭州人，教授，硕士生导师，博士，(E-mail)lige0717g@163.com。通讯作者：王婵(1990-),女，湖南湘潭人，硕士研究生，(E-mail)15700197513@163.com。

基金项目：湖州市重点科技创新团队项目(2012KC04)；国家自然科学基金项目(51375459)

收稿日期：2015-07-15