灯泡贯流式水轮机尾水管流动特性分析

敏 政, 李秋桐, 李琪飞, 张毅鹏, 李正贵，邓育轩(. 兰州理工大学 能源与动力工程学院，兰州 730050； . 南昌工程学院 机械与电气学院，南昌 330099)

0 引 言

贯流式水轮机是适用于低水头，大流量的水电机组[1]，由于河流上游流量的不稳定，机组需要经常改变运行工况[2]，特别是在非协联工况下，水轮机内部流态会急剧恶化，对过流部件的空化性能会产生很大的影响[3]。叶片和导叶之间漩涡与尾水管涡带是引起压力脉动的重要原因之一，其中尾水管涡带所引起的低频振动引起众多学者兴趣。当水轮机在偏离于最优工况点运行时，尾水管中的会产生空腔涡带，且其涡带形态与此时水轮机负荷的大小有着密切的关系，在低负荷时出现螺旋状偏心涡带，高负荷时产生柱状涡带。尾水管内流场的特性会因为空化涡带的形态变化而随之改变。杨静[4]采用LES模型对混流式水轮机尾水管内涡带引起的压力脉动进行了研究。夏林生[5]等对灯泡贯流式水轮机在飞逸状态下进行了全流道的数值模拟，计算了此过渡过程中尾水管内涡带的演变规律。季斌等[6]通过计算小流量工况下过流部件之间的动静干涉作用以及涡带的演化过程。钱忠东等[7]采用大涡模拟湍流模型，对灯泡贯流式水轮机额定工况下和偏工况下进行了计算，分析不同流量下尾水管内产生的涡带对压力脉动的影响，并与实验数据进行了比较。王磊等[8]基于气泡两相流的方法，对白鹤滩模型水轮机进行定长和非定常计算，预估了水轮机转轮和尾水管内空化的发生情况，并与实验结果进行了比较。由于灯泡贯流式水轮机在国内研究起步较晚，因此相关的一些研究多见于国外[9-11]。

本文采用汽液混输相均质假设和基于组分输运方程的空化模型，通过求解汽液混相均质流的雷诺平均N-S方程以及汽相组分输运方程，并考虑不可凝结汽相的影响，计算了贯流式水轮机尾水管内部的空化流场和压力脉动变化特点。

1 基本参数和计算工况

1.1 基本几何参数

根据提供的基本参数，以Pro/e为三维建模软件，图1为建立从进口到尾水管出口的全流道几何模型，图2为转轮的几何模型，表1列出了水轮机基本参数。

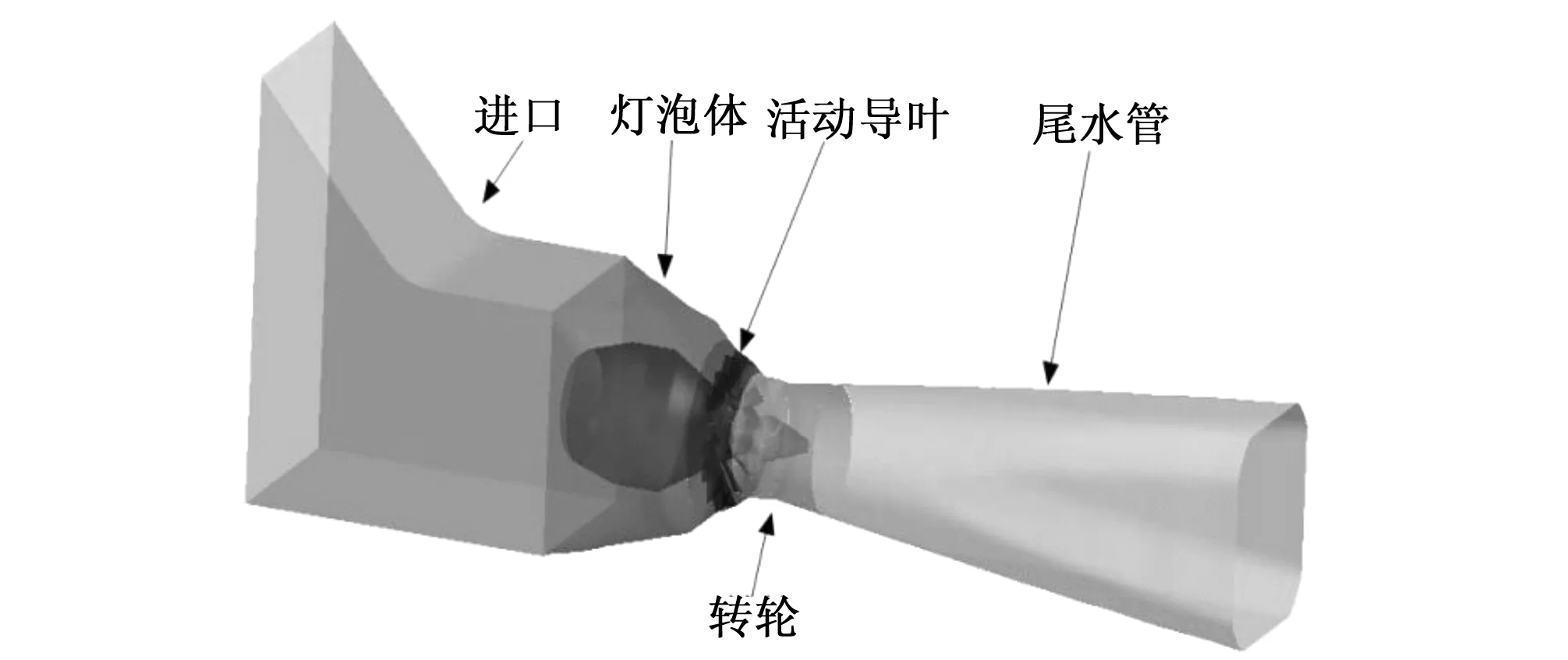
图1 水轮机全流道三维实体图Fig.1 The geometrical model of tubular-turbine

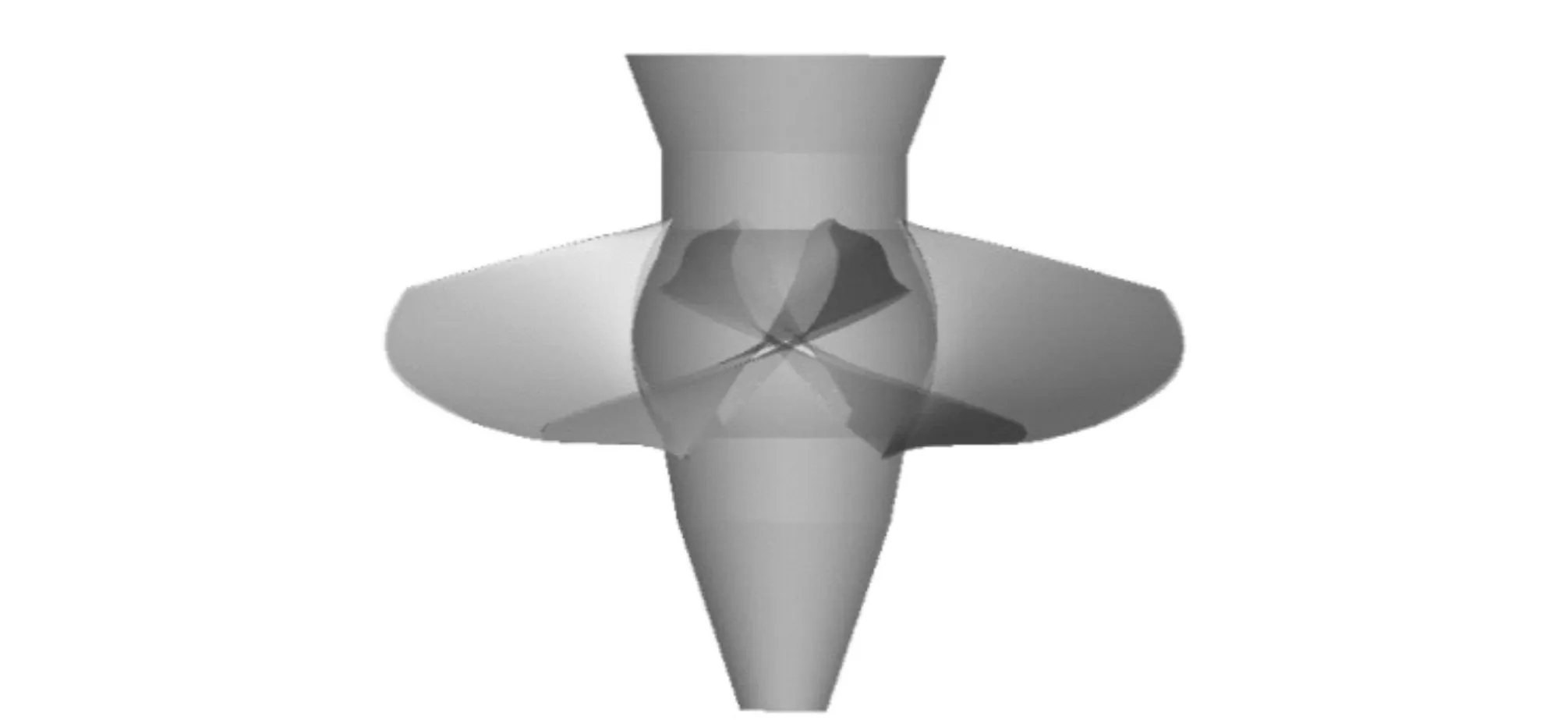
图2 叶片示意图Fig.2 The sketch of blades

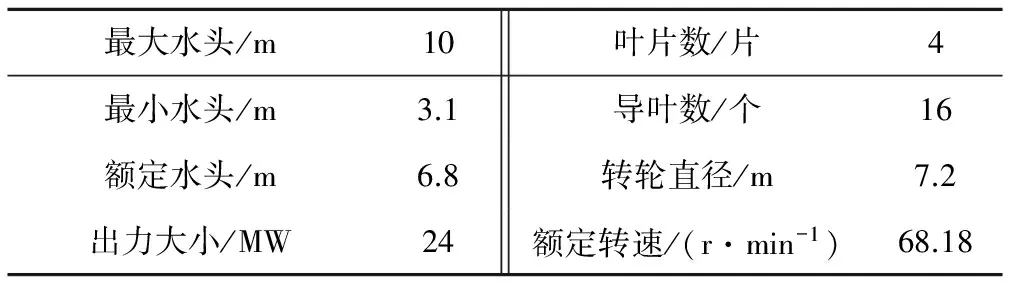
表1 水轮机主要参数Tab.1 Main characteristics of the tubular turbine

1.2 网格参数

对几何模型进行网格划分，采用ICEM网格划分软件对进口区域，尾水管和流道进口划分为六面体结构化网格，对转轮和导叶划分为四面体非结构化网格。为了减小网格数对计算结果的影响，对设计工况点进行网格无关性假设，最终确定的网格数为10 065 610，节点数为2 788 414，计算所用的网格如图3所示，网格无关性假设，如图4所示。

图3 水轮机全流道网格图Fig.3 Mesh of turbine

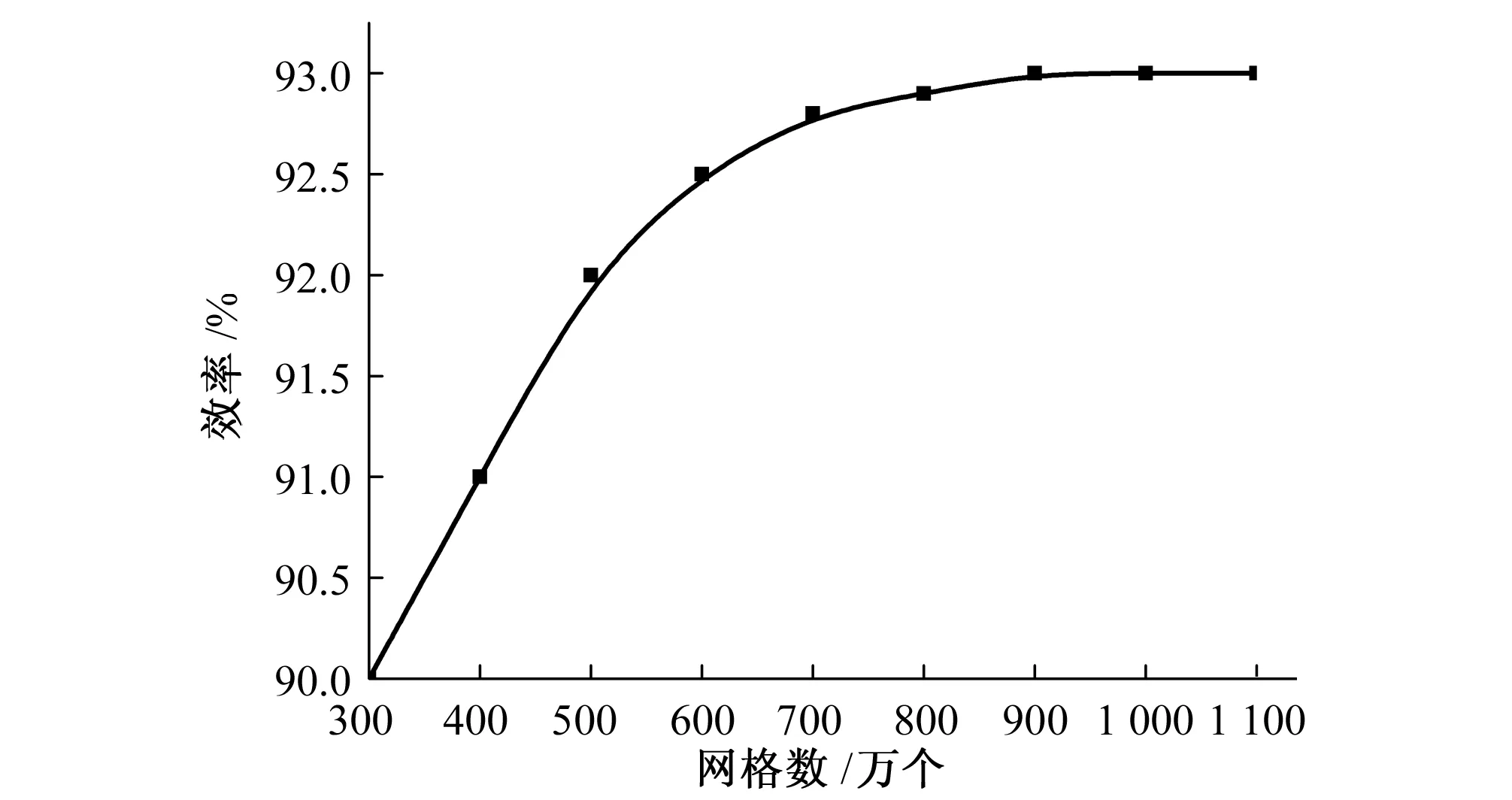
图4 网格无关性假设Fig.4 Verifying grid independence

2 数值计算方法

2.1 数学模型

由Rayleigh-Plesset方程得到的空泡特性和考虑各种影响的空化模型,水轮机中空化流动计算的连续性控制方程描述如下。

(1)混合流体的连续性方程：

(ρ)+▽·(ρv)=0

(2)汽相的连续性方程：

(ρf)+▽·(ρfv)=Re-Rc

蒸汽生成率 ：

蒸汽凝结率：

(3)混合流体的动量方程：

▽ (ρvv)=

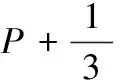
式中：ρ为水流相和空泡相形成的混合流体质量密度；v为混合流体的速度矢量；f为空泡相的质量组分；Re为水蒸气的生成率；Rc为水蒸气的凝结率；P为静压力；μ为分子黏性系数；μt为湍流黏性系数；g为重力加速度矢量。

由于采用了混合流体处理水轮机内部的空化流动，因此湍流模型中的和在形式上与单相流动相同，但其中的混合变量均为混合流体的平均量。计算中的物性参数取工作水温为25时的值，根据水轮机的实际运行情况，其中汽化压力=3 540，水-空泡表面张力-0.071 7 NM，假定水中不凝结性气体的质量组分为1×10-5。

2.2 离散和湍流模型

对计算区域采用混合网格，采用有限体积法对上述方程进行离散求解。时间项采用全隐世离散，扩散项和离散相采用中心差分格式，动量方程的对流项采用二阶迎风差分格式，变量储存在控制体中心，压力和速度采用SIMPLEC算法进行耦合求解。由于水轮机在偏工况运行时，存在漩涡，二次流等复杂流态，本文定常计算使用RNG k-ε模型代替标准的k-ε模型，非定常计算采用SST湍流模型，空化模型选用基于输运方程模型的Singhal完全空化模型[9,10]。

2.3 边界条件

为了模拟真实情况下水轮机内部的流动情况，在计算流动区域进口面上根据流量给定速度条件，并假定速度垂直于进口面；出口边界条件：自由出流；壁面边界条件：采用无滑移边界条件。初始流场条件：设置导叶和桨叶开度为某一固定值，通过三维定长计算得到流场结果，以此作为非定常计算的初始结果。为了预测尾水管的压力脉动，全文进行全流场的非定常湍流计算，考虑后期进行频谱分析的需要，计算的时间步长定位转轮旋转一圈的1/360，转速n=68.18 r/min，得到非定常的时间步长为0.002 444 5 s。

3 计算监测点位置与试验

3.1 计算监测点

从导叶段到尾水管一共取了6个截面，截面A位于导叶出口处，截面B位于转轮出口处，截面C位于轮毂尾部，截面D为尾水管进口处，截面E，截面F位于尾水管中后部，在每个截面上均匀取四个监测点，共有24个监测点。如图5所示。

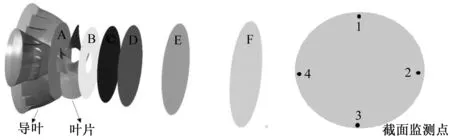
图5 监测点位置分布图Fig.5 Positions of sampling points

3.2 模型试验

为了保证几何模型建立的准确性，对所计算的结果与模型试验进行了对比。本次的模型试验由东方电机股份有限公司承担，如图6所示，试验台参数均满足ICE所规定的要求[11]，图7为在额定水头下数值计算和模型试验的效率变化曲线。

图6 试验现场Fig.6 Test site

通过图7线可以看出，效率的变化趋势基本一致。在较大空化数下，空化并没有对水轮机的外特性产生明显影响，效率基本保持不变。然而当空化数降低至初生空化附近时，效率曲线出现小幅度下降，其原因可能是由于少量的空化气泡出现在叶片出口边附近时，转轮出口速度矢量的方向发生了改变，尾水管进口的轴向速度有所增加，因此效率略微下降。

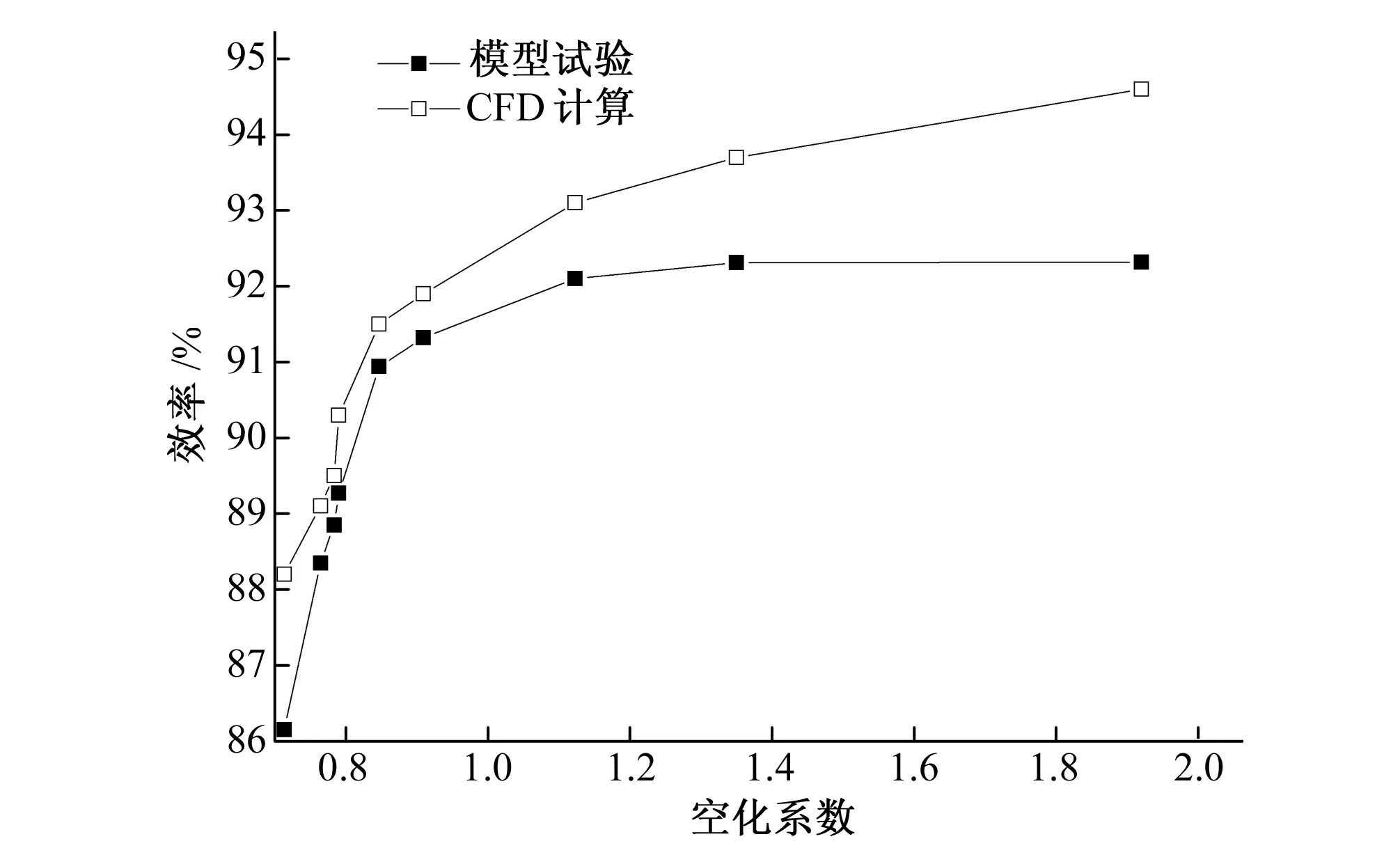
图7 效率变化曲线Fig.7 The curves of efficiency

随着出口压力的进一步降低，较大范围的空化气泡产生在叶片区域及尾水管内，严重阻塞流道致使流量及输出功率降低，进而导致效率曲线明显下降，效率下降3%时的空化点即为临界空化点。然而受到计算精度及非定常计算的数值模型等因素的影响，数值计算的结果略高于实验得到的结果。

4 计算结果与分析

4.1 定常计算结果

图8为在不同空化系数下流场内压力和流线分布。从图8中可以看出，随着空化系数的降低，流道内的流线密集程度逐渐在降低，说明流道内的流体流通性较好，没有发生边界层分离，二次流和漩涡等干扰正常流动的因素较少，这时流场比较稳定，水力损失少。当空化系数继续降低后，转轮出口处压力持续下降，在尾水管内出现的“柱状”低压区面积增大，此时流道内空化发生加剧，含有气体的空泡附着在叶片表面，降低了叶轮的做功能力，并且气泡充满流道阻碍了水流的正常流动，使流道内流场结构产生了巨大的改变，致使水轮机的效率继续降低，这与图7中所显示的效率变化是相符的。通过定常计算，数值模拟的效率和模型试验的结果相差不大，说明了本次计算的准确性和数值计算的可靠性。

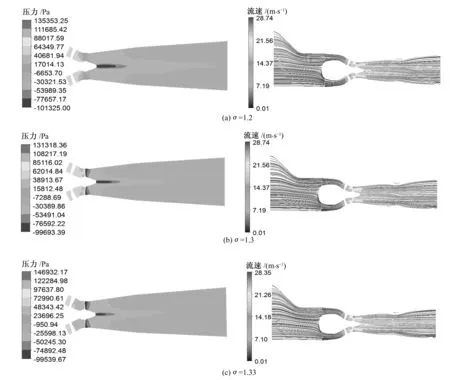
图8 不同空化系数下流道内压力和流线分布Fig.8 Pressure and streamline contour in different cavitation coefficient

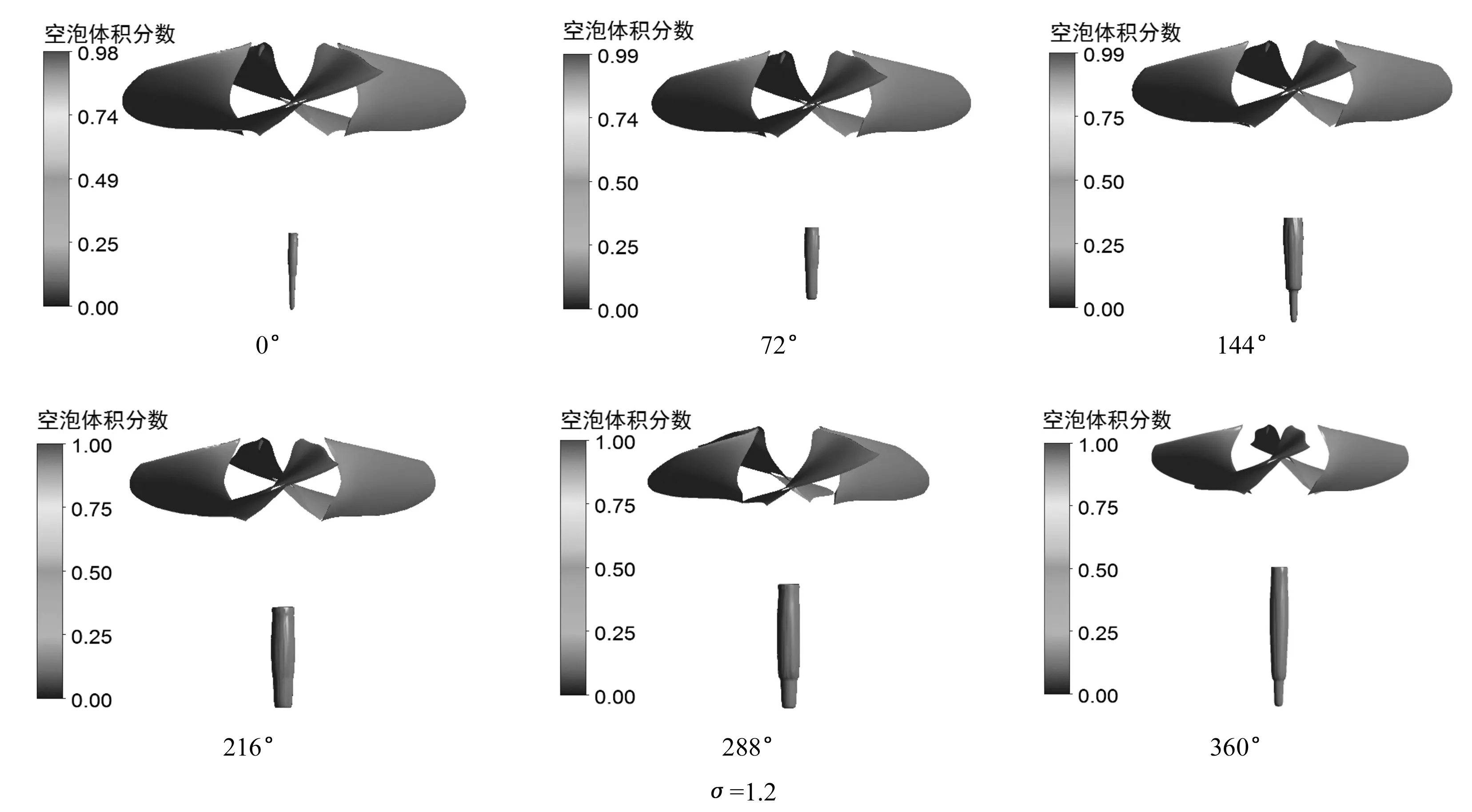
图9 尾水管涡带形态Fig.9 Pattern of vortex rope in draft tube

4.2 非定常计算结果

图9为在空化系数σ=1.2尾水管内涡带随时间的变化图。从图9中可以看出，在水轮机尾水管内的空化涡带形态呈现为接近“柱状”，涡带长度以及直径均随着时间的变化而演变。在转轮转动一个周期刚开始时，在尾水管内出现体积较小的柱状空化涡带。随着时间的向后推移，空化区域逐渐增大，空化涡带体积变化剧烈，在涡带体积增大的过程中，尾部会出现脱流；当到达0.6t时，涡带的尾部直径会出现很明显的突然减小，这种现象称之为“环形水跃”，Dorfler[12]在使用两相流对空化涡带进行数值模拟中也发现了这个现象，并且这种现象在单相流的模拟中不会出现。这与Alligne S[13]等所研究的现象是一致的。当转轮周期继续增加时，尾水管内的空化涡带直径及长度仍会继续增大，此时尾水管内空化已经发展至非常严重的程度，大量的气泡会堵塞流道。环形水跃现象一般解释为：柱状空化涡带主要通过体积波动来影响流场，但空化涡带本身也是在不断旋转的，受尾水管扩散段及下游流场的影响，空化涡带的尾部附近流场压力会越来越高，空泡体积浓度越来越低，因而无法继续形成直径较大的空化涡带，所以会出现突然的水跃。随着空化涡带体积波动过程，涡带环形水跃以下直径较小的部分会出现频繁的空泡增长和脱落现象。

4.3 压力脉动计算结果分析

图10为图5中所示截面中监测点1处的压力脉动时域图。由图10中可以看出，所检测截面上压力的相位和脉动周期均表现出了相似的变化规律，但是流体经过转轮做功后使这些位置表现出不同的压力脉动特性。从导叶出口处到尾水管内所监测的截面上可以看到，在导叶出口处，由于并未发生空化，所以此处压力值与其他部分相比较高，压力波动平稳；在转轮出口处因为发生了空化，此处的压力波动剧烈，在一个大的波动后出现若干个较小的脉动区域，随着时间的向后推移，这种变化会不断地持续下去，压力在数值上呈现出剧烈下降趋势，这与流场中所展示的压力变化是相吻合的；随着在轮毂末端区域出现明显的柱状空腔涡带，沿着水流方向尾水管两侧呈现出对称性延生分布，且涡带区域有着不断扩大的趋势，表现出了极强的不稳定性，因而压力进一步降低波动更加剧烈；在尾水管中段，涡带消失，空化涡带由于自身的旋转作用的减弱而对内部流场的压力影响同样愈见下降，此时压力数值回升，所以表现为监测面E和F上压力脉动的相位差也愈来越小，波动趋于平缓，这对于尾水管的压力回复性能提高是有利的。当空化系数降低时，整个流场内压力波动加剧，并且压力数值大幅降低，这是由于空化发生更加剧烈所导致的。

水轮机在稳定运行过程中，机组的转频为fn=1.123 6 Hz，对计算数据进行快速傅里叶变换得到频域图。

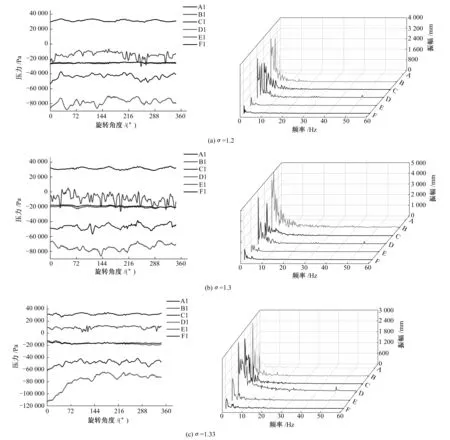
图10 监测断面压力脉动时域图和频域图Fig.10 Frequency spectra of pressure fluctuations at different sections

图10中右侧为在3个空化系数下相应截面监测点1的压力频谱，3个工况下的结果比较类似，转轮出口处、尾水管内转频为4fn，为叶片通过频率，此时频率下压力脉动的幅值较小；轮毂末端和尾水管进口处的转频为0.8fn，属于低频压力脉动，这时压力脉动幅值相比较大，这是因为柱状空化涡带工况尾水管进口处流场出现“环形水跃”现象，导致涡带尾部受到水流产生的脱流现象而导致空泡不断发生溃灭的影响，这时流场内部出现十分明显的流量不均匀性，这就是导致压力脉动幅值在此处高于其他地方的原因。

不同频率的压力脉动同时向着上游和下游同时传播开来，与此同时幅值不断降低，说明幅值会随着距离的增加而降低，最小幅值出现在尾水管中段，这是由于此处涡带已经逐渐消失，受到涡带影响很小，流体运动平稳。从图10中还可以看出，除了空化涡带所占据的主频以外，流场中还存在一个空化涡带所引起的频率为5fn的次频，从B、C、D 3个截面可以明显看出其对于流场的影响，这和图9中出现的小幅动的压力波动相对应。随着空化系数的降低，压力脉动幅值增大，这是由于流道内空化发生加剧，形成各种复杂的空化漩涡，特别是在轮毂末端和尾水管进口处不断增强空腔涡带，诱发了大量的低频高幅压力脉动，易引发由于空化涡带产生的噪声。导叶和转轮之间截面A中监测点压力脉动主频为fn=4.54 Hz，接近转轮的叶频，这主要是由于转轮在旋转过程中切割活动导叶所形成的射流-尾迹产生强烈的动静干涉作用，在此作用下，造成了频率较高的低幅压力脉动，因而很容易引起机组的振动。此时压力脉动的最大幅值ΔH/H达到6.7%，幅值沿着下游方向减小，动静干涉作用随着逐渐远离叶轮而影响逐渐降低。

5 结 论

(1)随着时间的变化，空腔涡带的体积逐渐增大，涡带的长度增幅远大于直径的增幅，涡带分布均匀，位于尾水管中部；在涡带的尾部由于不断出现的小的空泡脱流及溃灭，从而导致了涡带尾部出现“环形水跃”现象。

(2)涡带出现时，尾水管内所取的截面监测点位置处压力脉动的相位差并不是完全相同的，尾水管内压力脉动以低频为主，涡带主频为转频，其余频率由涡带公转产生以2～5倍主频的次频；从转轮出口到尾水管进口处压力脉动变化最为剧烈，这与此处产生空腔涡带有关；随着空化系数的逐渐降低，监测点处压力脉动变化更加剧烈。

(3)压力脉动对空化系数的变化很敏感，空化系数越低，压力脉动越严重，会降低机组运行中的稳定性，使水轮机的水力效率下降。

□

[1] 程良骏.水轮机[M].北京:机械工业出版社,1981.

[2] 于 波,肖惠民.水轮机原理与运行[M].北京:中国电力出版社,2008.

[3] 扬 波，李培根.贯流式水轮机转轮试验研究[J].东方电机,2001,(1):41-47.

[4] 杨 静, 混流式水轮机尾水管空化流场研究[D].北京:中国农业大学,2013.

[5] 夏林生,程永光，张晓曦.灯泡式水轮机飞逸过渡过程3维CFD模拟[J].四川大学学报(工程科学版),2014,46(5):35-41.

[6] 季 斌,罗先武，西道宏.混流式水轮机涡带工况下两级动静干涉及其压力脉动传播特性分析[J].水力发电学报,2014,31(1):191-196.

[7] 钱忠东,魏 巍,冯晓波.灯泡贯流式水轮机全流道压力脉动数值模拟[J].水力发电学报,2014,33(4):242-249.

[8] 王 磊,娄 瑜，王照福.混流式模型水轮机空化流动分析与试验研究[J].排灌机械工程学报，2014,32(9):771-775.

[9] Necker J,Aschenbrenner T. Model test and CFD calculation of a cavitating bulb turbine [C]∥ Proceeding of the 25th IAHR Symposium on Hydraulic Machinery and Systems. Timisoara:IPO Publishing,2010.

[10] Yang W, Wu Y L,Liu S H. An optimization method on runner blades in bulb turbine based on CFD analysis [J].Science China Technological Sciences,2011,54(2):338-344.

[11] Thaithacha Sudsuansee, Udomliat Nontakaew. Simulation of leading edge cavitation on bulb turbine [J]. Songklanakarin Journal of Science and Technology, 2011,(1):51-60.

[12] Zwart P,Gerber A G,Belamri T.A two-phase model for predicting cavitation dynamics[C]∥ Proceedings of ICMF 2004 International Conference on Multiphase Flow,Yokohama,Japan,2004:1-11.

[13] Mejri I,Bakir F,Rey R.Comparison of computational results obtained from a homogeneous cavitation model with experimental investigations of three Inducers[J].Journal of Fluids Engineering,2006,128(6):1 308-1 323.

[14] Liu Shuhong,Li Shengkai,Wu Yulin. Pressure fluctuation Prediction of a model Kaplan turbine by unsteady turbulent flow simulation[J]. Journal of Fluid Engineering,2009,131(10):101012.1-101012.9.

[15] Dorfler P K, Keller M,Braun O. Francis full-load surge mechanism identified by unsteady 2-phaseCFD[C]∥ Proceedings of 25th IAHR Symposium on Hydraulic Machinery and Systems, Timisoara,Romania,2010.

[16] Alligne S, Maruzewski P, Dinh T,et al. Prediction of a Francis turbine prototype full load instability from investigations on a reduced scale model[C]∥ Proceedings of the 25th IAHR Symposium on Hydraulic Machinery and Systems,Timisoara,Romania,2010.