小开河灌区地表水沙及地下水联合优化配置模型

孔 珂，徐 晶，王 昕，徐征和(.济南大学资源与环境学院，济南 500; .山东省水利科学研究院，济南 5003)

1 问题的提出

小开河灌区位于山东省滨州市，实际控制灌溉面积7.67万hm2，是黄河下游重要的大型引黄灌区。自建成以来，灌区年均引水近2.0 亿m3，持续稳定地在保障农业生产、改善群众生活等方面发挥着巨大作用。在当前水资源日益短缺的形势下，灌区的良性健康发展已成为区域社会经济可持续发展的重要支撑。然而，同黄河下游其他引黄灌区一样，小开河灌区当前也面临水资源供需矛盾加剧、地下水环境恶化以及泥沙淤积严重等问题[1-3]。与其他灌区不同，小开河灌区没有在渠首建设沉沙池的条件，因而将其设在了渠道中部，需要在输水的同时将泥沙长距离输送入池以避免渠道淤积。从实践情况看，小开河灌区较好地实现了长距离输沙的设计目标，基本实现了不冲不淤[4]，但其防淤压力一直很大。对此，相关学者已在地表地下水联合调度、水盐平衡分析、水沙调度及泥沙资源化等方面取得了许多成果[2-6]。从系统的角度看，这些问题都源于灌区地表、地下以及引黄水的时空配置，同时问题的解决也以水资源配置的最终效果为目标，因此，有必要针对水资源供需矛盾、地下水环境保护以及泥沙长距离输送这三大问题综合优化小开河灌区的水资源配置方案。

2 模型的建立

小开河灌区输水干线自南向北分为输沙渠、沉沙池、输水渠三部分，总长89.3 km，设有支渠31条，涵盖5县18个乡镇，除农业灌溉外，还向滨州市的西海水库以及无棣县的北海水库这两座主要用于城镇用水的水库供水。按照供水顺序和用水关系，本模型将用水区域从(干渠)上游到下游依次分为滨城区、开发区、惠民、阳信、沾化、无棣6个子单元，以月为决策时段长，先以水资源配置总体效益为目标建立优化模型，然后分别以输沙效果以及地下水位控制为目标建立两个子模型，最后用分层序列法将3个模型耦合起来。

2.1 水量分配效益模型

水资源效益模型就是从水资源供需和利用效率的角度出发，将不同的水源在不同的时间分配到不同区域的不同行业中，在满足各类供需水限制的前提下，尽量使整体效益最高。

小开河灌区的水源有引黄水、地表水、地下水和内河客水。用水行业分为农业灌溉用水、工业用水和城乡居民生活用水等，其中农业灌溉用水又分为粮食作物用水和经济作物用水。水量分配的限制条件包括引黄能力约束、地表地下可用水资源量约束、灌溉需水约束、工业需水约束、生活需水约束等。

2.1.1目标函数

(1)

式中：Wri,j,k，Wgi,j,k，Wdi,j,k分别为k时段i行业(农业取1)地表水，地下水，引黄水使用量；αi,j,βi,j,γi,j分别为i子区行业j行业引黄水，地表水，地下水利用净效益。

2.2.2约束条件

(1)水量平衡。任何时间段各子区内各行业的引黄水使用量之和等于各子区有效引黄量：

(2)

式中：Wtk为k时段引黄总量；ηi为i子区引黄水渠道水利用系数。

(2)供水能力约束。任何时间段的各类引水总量不能超过其水源可供水量，由于内河客水较少，所以按引黄水、地表水、地下水三类考虑：

(3)

式中：LWri,k,LWgi,k分别为k时段i子区地表、地下用水量限制；LWdk为k时段设计引黄水量上限；TWy为全年有效引黄水可用总量。

(3)需水约束。

(4)

式中：Di,j,k，Gi,j,k分别为k时段i子区行业j行业最低，最高需水量。

(4)非负约束。

(5)

2.2 输沙模型

小开河灌区需要长距离输沙，因此除了一般的防沙减淤措施外，在水沙调度方面有更高的要求。在“小开河引黄灌区泥沙长距离输送与优化配置”(中国水利水电科学研究院、滨州市水利局，2009年)课题中，科研人员和灌区管理人员在引水调度方式、支渠口门的运行管理等六个方面研究总结了保障小开河灌区泥沙长距离输送和水沙优化调度的具体措施。本文选出其中与水量配置有关联的部分，将它们转化为不同的数学形式，如表1所示。建立输沙效果子模型。

表1 具体措施模型化Tab.1 Modelling practical measures

2.2.1目标函数

本部分有两个目标函数：①黄河水含沙量低时，应多引水，反之应少引水；②小流量引水时，应尽量先满足前面的用水单位。 对于①，可将其表达为尽量使低含沙量期间的引水总量与高含沙量期间的引水总量的差值最大。相比较而言，黄河主汛期7-10月份的含沙量较高，为高含沙时段，其他月份作为低含沙时段，其形式为：

(6)

式中：Ω为指标集，表示黄河含沙量小的月份。

对于目标②，由于在引黄期间各单元引水时间基本一致，为求解方便，可将其转化为引黄水量小时尽量满足上游地区。考虑到高含沙期引黄水量本身就较小，那么就可将两个目标结合起来，即将目标①中的上游区域(前3个区)低含沙期的作用弱化，同时将其高含沙期的作用强化，这样既能实现控制高含沙期引水总量的目的，又能尽量使其分布在上游区域，从而将水沙模型由两目标转化为单目标。其形式为：

(7)

式中：π为调节系数，取0.05～0.1；∏为上游区域集合。

2.2.2约束条件

最低流量约束：供水期的平均引水流量不低于3/4设计引水流量

Wtk/htk≥0.75Id

(8)

式中：htk为k时段引黄闸引水时间；Id为引黄闸设计流量。

2.3 地下水位控制模型

灌区地下水资源主要分布在滨城、惠民、阳信、无棣四县区，其中滨城、惠民地区较为丰富，且具有较好的开采条件，但因有引黄河水的便利条件，利用程度较低；下游地区虽有一定的水资源储量，但是埋深较深，开发费用较高，利用程度也很低。

目前，灌区地下水开发利用中的环境问题主要是防止土壤次生盐渍化以及下游滨海地区的海水入侵，其关键就是控制地下水埋深。根据《滨州市地下水超采区成果报告》(滨州市水利局，2004年)，小开河灌区较为合理的埋深范围是3～6 m。

从1986-2012年的地下水位观测资料看，灌区的地下水埋深较浅，普遍不到3 m。所以，本模型以灌溉过程中地下水水量平衡为基础，将3 m作为模型的目标，即埋深越接近3 m越合理，将6 m作为控制约束，即埋深不能超过6 m。

2.3.1目标函数

(9)

式中：msi,k为i区域k时段的地下水埋深。

2.3.2约束条件

(1) 水量平衡约束。忽略灌区各地区之间水平方向水量交换，地下水埋深的变化由水量平衡得出：

msi,k+1=msi,k-[ωi·Pi,k·F+

(Wdi,1,k+Wri,1,k)(ξi+σiρi)+Wgi,1,k(θi-1)]/(μiFi)+

ETi,k

(10)

式中：Fi为i子区面积；ωi为i子区降雨补给系数；Pi,k为i子区k时段降雨；σi为i子区渠系水利用系数；ρi为i子区灌溉入渗补给系数；ξi为i子区渠系入渗补给系数；θi为i子区井灌回归补给系数；μi为i子区的给水度；ETi,k为i子区k时段地下水蒸发强度；Wdi,1,k为i子区k时段农业用引黄水量；Wri,1,k为i子区k时段农业用的地表水量；Wgi,1,k为i子区k时段农业用地下水量。

(2) 地下水埋深约束。地下水埋深的下限为6 m：

msi,k≤6

(11)

3 模型求解

3.1 模型耦合求解方法

本模型是一个多目标模型，各子模型的目标函数的量纲不同，无法直接求解。本研究采用分层序列法[7]，以水资源分配效益为主目标， 依次将输沙效果子模型和地下水控制子模型耦合进来，逐步求解，每次都在前一个目标函数的最优解集中求解下一个目标的最优解。为保证求解的成功，这里按照80%的控制标准将前一步的最优解扩展为最优解集，作为约束条件嵌入下一步的求解。

本次计算的水平年选择降雨P=50%和P=75%，所需降雨、引黄、地表地下水、水文地质参数、社会经济参数来自小开河灌区的设计资料、“十二五”规划资料以及相关部门的统计资料。

3.2 求解过程

(1)水量分配效益模型的求解。由于模型比较复杂，这里采用专业优化软Lingo11求解，该软件具有较快的速度和较高的可靠性。求解2.1节的模型，得到50%水平年时最大效益为9.182亿元，75%水平年时为8.763亿元。该结果只考虑了水量分配效益。

(2)水量-输沙模型的求解。将上一步求得的最优效益的80%作为约束条件，连同其他水量约束耦合到2.2节的输沙效果模型，得到水量-输沙模型，如式(12)所示。

(12)

求解该模型可以得到50%水平年时最优输沙目标值为1.257亿m3，效益目标为8.789亿元；75%水平年时最优输沙目标值为1.113亿m3，效益目标为8.362亿元。该结果综合考虑了水量配置效益与输沙效果。

(3)水量-输沙-地下水模型的求解。将模型(12)的最优输沙目标的80%作为控制条件，连同其他水量-水沙约束一起耦合入2.3节的地下水位控制模型，得到水量-输沙-地下水模型，如式(13)所示。

求解模型(13)，可以得到50%水平年时地下水控制目标的最优值为 122.706，此时水量分配效益为8.733亿元，水沙目标为1.257亿m3；75%水平年时地下水控制目标的最优值为 81.299，水量分配效益为8.251亿元，水沙目标为1.113亿m3。该结果综合考虑了水量配置效益、输沙效果、地下水位控制三方面的因素。

(13)

4 结果分析

为便于分析分层求解效果，在依次求解上述3个单目标模型的同时，也分别计算出其他两个目标，50%水平年的计算结果如表2所示，75%水平年的计算结果如表3所示。

从表2、表3可以看出，两种水平年下的计算效果都是逐层优化的。水量模型只考虑了经济效益，不考虑其他限制，因此其得出的效益结果必然是最大的经济效益，经过水量-输沙模型和水量-输沙-地下水模型的逐步优化之后，虽然两种情况下的效益值都有所下降，但最后仍都保持在最优值的95%以上；水沙目标经水量-水沙模型优化后都有一定的提高，并且在最后的方案中也都没有下降，而地下水目标则在水量-输沙-地下水模型中比最初均改善了40%以上，效果明显。因此，可以看出，利用本模型得出的最终的方案是比较均衡的方案，即我们通过分层序列法的逐步优化，得到了综合考虑输沙效果与地下水水位控制的水量优化配置方案。

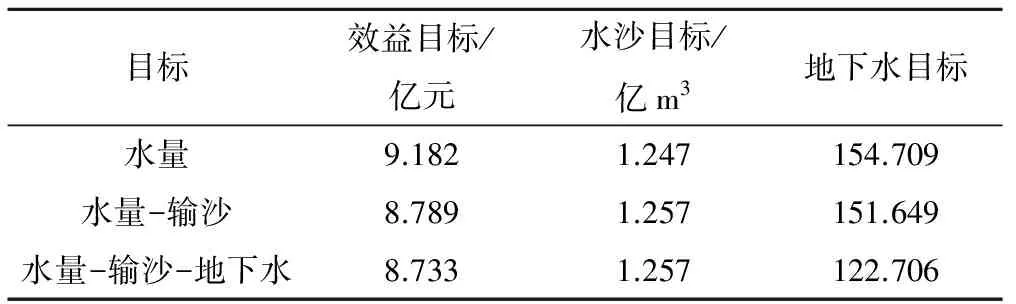
表2 50%水平年的分层优化结果对比Tab.2 Hierarchy optimal results comparation in 50% level year

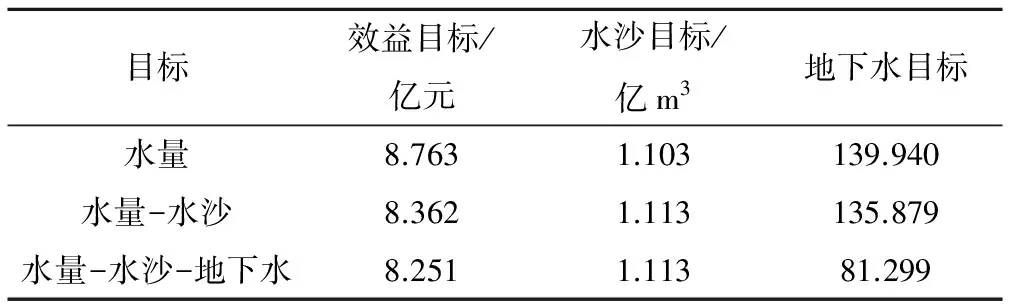
表3 75%水平年的分层优化结果对比Tab.3 Hierarchy optimal results comparation in 50% level year

5 结 语

水资源供需矛盾、地下水环境保护以及长距离输沙这三大现实问题是小开河灌区水资源优化配置的重点问题。本文利用多目标优化模型对灌区水资源进行了优化配置，提出了综合配置方案，对灌区水资源科学管理有促进作用。由于条件所限，本方案以月为研究时段并且将整个研究区域概化成了6个单元，没能考虑更细致的时空差异，也没能将生态用水纳入模型。另外由于缺少确切的生产数据以及各类经济、环境实际效益值，所以在方案对比分析上比较欠缺，这些都有待于进一步研究完善。

□

[1] 吴登忠.齐河县引黄灌溉供水现状与发展对策[J].山东水利,2013,(4):54-57.

[2] 刘景华.黄河下游引黄灌区水盐分析与水沙调度技术研究[D].南京:河海大学,2006.

[3] 戴 清.引黄灌区有关问题与实现水沙配置的效益分析[J].中国水利水电科学研究院学报,2007,5(1):15-21.

[4] 毛伟兵,王景元,张玉明.小开河引黄灌区泥沙资源的合理利用与优化配置[J].山东农业大学学报(自然科学版), 2006, 37 ( 2): 231- 234.

[5] 岳卫峰.基于GAMS的内蒙古河套灌区水资源联合利用分析[J].南水北调与水利科技,2013,11(3):12-16.

[6] 王艳华.引黄灌区水沙资源优化配置[D].北京:中国水利水电科学研究院,2007.

[7] 尚松浩.水资源系统分析方法及应用[M].北京:清华大学出版社,2006.