灌溉用水效率尺度效应的模拟分析——以宁夏惠农渠灌域典型灌排单元为例

陈皓锐，韩松俊，王少丽，焦平金，管孝艳(.中国水利水电科学研究院 国家节水灌溉北京工程技术研究中心，北京 00048；2.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072)

灌溉用水效率具有尺度依赖性已被广泛接受[1-3]，回归水重复利用和空间变异性被普遍认为是导致这一现象的主要原因[4-6]， 由于回归水重复利用方式和数量的差异以及空间变异性影响的不确定性，灌溉用水效率尺度效应尚无统一结论，如Peter发现土耳其Gediz流域SRB灌区从田间到流域的灌溉水分生产率逐渐增大，原因是小尺度只计算了棉花的产量，而大尺度还包括了其他的作物[7]。Bastiaanssen等计算了渠灌水分生产率和腾发量水分生产率随面积变化的规律，结果表明两个指标基本都是随面积增大而逐渐减小，原因是上游土壤更肥沃引起的高产所导致[8]。崔远来、董斌等对湖北漳河灌区的不同灌溉用水效率指标随尺度变化的规律进行了揭示，结果表明回归水的重复利用使得大部分指标总体上呈现随尺度增大而变大的规律[9]。陈皓锐计算了河北石津灌区净入流量水分生产率随尺度变化规律，也发现了该指标随尺度增大而增大[10]。可见，不同区域、不同水循环特征、不同内涵用水效率指标、不同回归水重复利用方式都可能导致用水效率尺度效应出现结论的差异。

本文以宁夏惠农灌域某个300 hm2的典型灌排单元为例，利用修改后的干旱区绿洲散耗型水文模型进行不同尺度水平衡要素模拟，并计算了腾发量占净入流量比例和出流量占净入流量比例随尺度变化规律，模拟揭示了地表排水再利用和地下抽水两种重复利用条件下的灌溉用水效率尺度效应。

1 材料与方法

1.1 研究区概况和试验布置

研究区位于宁夏平罗县城以东8 km，属惠农渠灌域第6管理所范围，多年平均降水量183.4 mm，蒸发量1 701.7 mm。区域总面积299.6 hm2，灌溉面积281.3 hm2，其中旱作物(小麦、玉米和蔬菜)面积占85.3%，水稻面积占14.7%。按照斗渠供水范围不同划分为4个地块，水稻集中在地块2和地块3。区域主要由南北两条支渠(新建渠和大张渠)及其所属的四条斗渠供水灌溉，并通过区域中心的支沟进行排水。灌溉时由昌润渠(干渠)分水至大张渠和新建渠，再分配给各条斗渠后进入田间进行灌溉，排水时首先汇入区域中心的支沟，再进入第五排水沟流出研究区外。在地块2末梢处设置的泵站利用支沟排水对地块2进行灌溉，在地块3末梢和地块4的东部设有两个机井抽取上游汇聚的地下水对各自地块进行补充灌溉。

图1 研究区示意图Fig.1 Sketch map of the study area

田间试验观测和数据收集项目包括渠道灌溉水量、气象数据、地下水位、机井抽水量、沟水回用量、土地利用和种植结构以及典型沟渠断面参数。观测试验从2013年10月份冬灌开始至2014年10月份冬灌前结束。

(1)灌溉水量：四条斗渠共10个进水口，灌溉期间记录每个进水口的开关闸时间，并利用流速仪测量灌溉流量，测量频率为每天两次。

(2)气象数据：从距研究区7 km的平罗气象站获得，用于计算参考作物腾发量。

(3)地下水位：根据作物分布状况共布置15眼地下水位观测井，利用自动水位计记录地下水位变化。

(4)回归水重复利用量：分别利用水表对沟水回用量和机井抽水量进行计量，得到不同地块回归水重复利用量。

(5)土地利用和种植结构：利用GPS对研究区土地利用和种植结构进行调查，得到不同地块不同作物种植面积。

1.2 尺度界定和用水效率计算

本研究从上游往下游逐级嵌套累加划分为A/B/C/D四个空间尺度。空间尺度划分情况见表1和图2。

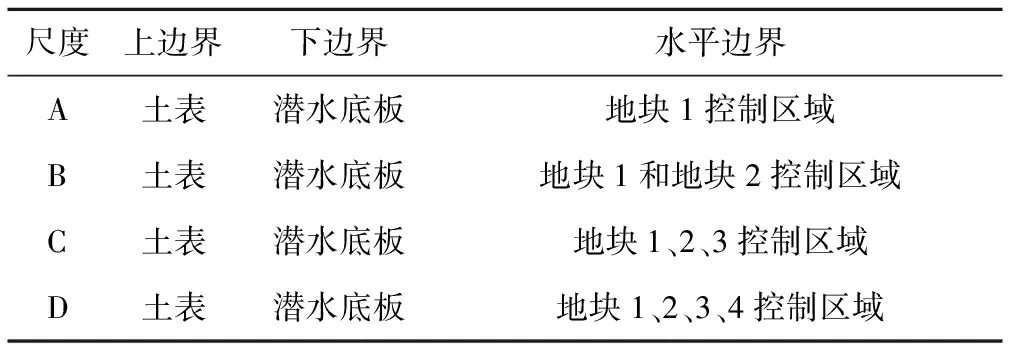
表1 空间尺度的边界说明Tab.1 Spatial scales definition

图2 空间尺度划分示意图Fig.2 Sketch map of different scales

本文选择腾发量占净入流量比例和出流量占净入流量比例两个灌溉用水效率指标进行不同尺度的评估及尺度效应分析。各个指标计算公式如下。

(2)

式中：FRi为腾发量占净入流量比例；FRoi为出流量占净入流量量比例；k为下标，地块编号，从上游往下游依次为1～4；t为下标，地块总数，4；m为下标，作物种类编号；n为下标，作物种类总数；ET为作物腾发量；P为降雨量；Ick为斗渠引水量；Igk为地下水抽水灌溉量；ΔS-土壤水库蓄水增加量；ΔG为地下水库蓄水增加量；R为地表排水量；Out为地下侧向出流量；In为地下侧向入流量；GR为地下排水量。

1.3 水循环模拟模型

本文利用干旱区绿洲散耗型水文模型(“四水转化”模型)进行研究区的水循环模拟，该模型基于水量平衡原理，对干旱区灌域的水资源引用、转化、消耗和循环过程进行分区模拟，已应用于塔里木河流域多个绿洲灌区和内蒙古河套灌区[11-13]。模型将各个分区分为灌溉地和非灌溉地，然后细分为农地/非农地、沟渠、水库、泉、井等多种均衡单元分别进行模拟，不同均衡单元和分区之间通过地下水侧向流动、渠道分配水、沟道排水汇流等过程建立水力联系。灌溉地水分转化关系复杂，在土壤垂直剖面上分为上部土壤层(非饱和带)和下部地下水层(饱和带)，考虑地表水、土壤水和地下水的转化。非灌溉地土壤水变化不大，在土壤垂直剖面上不区分上部土壤层和下部地下水层，只考虑地表水和地下水的转化。河段、泉、井、水库、湖泊等水均衡单元、因各自的地表水、土壤水和地下水联系紧密，在垂直方向不加区分，重点考虑地表水入流和出流及地表水和地下水的转化。

根据研究区实际情况，对“四水转化”模型进行了适当简化和修改，主要包括如下几个方面：①灌溉水源增加地下抽水，并在地下水循环和地下水位计算时将抽水的影响纳入考虑；②由于本研究主要关注灌溉地，因此不考虑不同类型非灌溉地之间也可能发生的地下水的侧向交换；③根据资料搜集状况，将原模型模拟时长由月尺度改为日尺度；④由于研究区土地利用相对简单，不考虑水库、泉等单元的水循环过程。

2 结果分析

2.1 水循环模型率定和验证

采用2013年冬灌至2014年夏灌前实测地下水位对模型参数进行率定，采用2014年夏秋灌期间实测地下水位对模型进行检验。图3为不同地块实测和模拟的平均地下水埋深对比。从图3上可以看出，模拟值与实测值变化趋势具有较好的一致性，部分数据之间存在偏差的可能原因如下：①每个分区内的不同田块并不是同时灌溉，不同田块的灌水时间存在差异，而模拟时采用相同的灌溉量和灌溉时间与实际情况存在一定差异；②模拟的时间间隔为1d，与实际灌溉情况存在一定差异；③冬灌后由于土壤冻结，灌溉对地下水的补给小于模拟值，土壤化冻后，由冬灌蓄存在土壤的水分将对地下水形成补给，此时虽然没有灌溉但地下水位在4月初会较快上升，模型对此仅根据地下水埋深概化对地下水的补给；④假定计算区域内的土壤质地是均一的，与实际情况可能存在一定差异。

图3 不同地块地下水埋深模拟值与实测值对比Fig.3 Computed vs. observed groundwater depth in different fields

将不同地块地下水埋深的模拟值与实测值绘制在同一张图中，见图4。

为进一步说明模型模拟效果，采用平均残差比例、分散均方根比例、相对误差和Nash-Sutcliffe效率系数4个统计参数对模拟效果进行分析。各统计参数计算公式如下。

平均残差比例：

(3)

分散均方根比例：

(4)

图4 率定和验证期地下水埋深散点图Fig.4 Scatter plots for groundwater depth in validation and calibration periods

相对误差：

(5)

Nash-Sutcliffe效率系数

(6)

根据上述公式可以分别计算模型率定期和验证期各个评价指标见表2。

对于一般模型，尤其是实测资料本身误差很大的情况下，认为RE小于15%，且Ens>0.5的时，模拟效果可以接受，参数较为可靠，可用于实际模拟应用。从各个统计参数的计算结果可以看出，平均残差比例、分散均方根比例、相对误差皆在15%以内， Nash-Sutcliffe效率系数在率定和检验期也都超过了0.5的临界标准。总体上来说，构建的水均衡模型的概化方式、各种参数取值基本是合理的，没有发生大的错误，它模拟的水平衡要素基本是理想的。

表2 水均衡模型模拟效果评价Tab.2 Parameters for the accuracy assessment of the hydrological model

2.2 研究区水平衡分析

利用构建的水平衡模型对作物生育期不同地块水均衡进行模拟，得到研究区水均衡图，见图5。

根据图5可以得到不同尺度和不同地块水均衡框架。见表3。

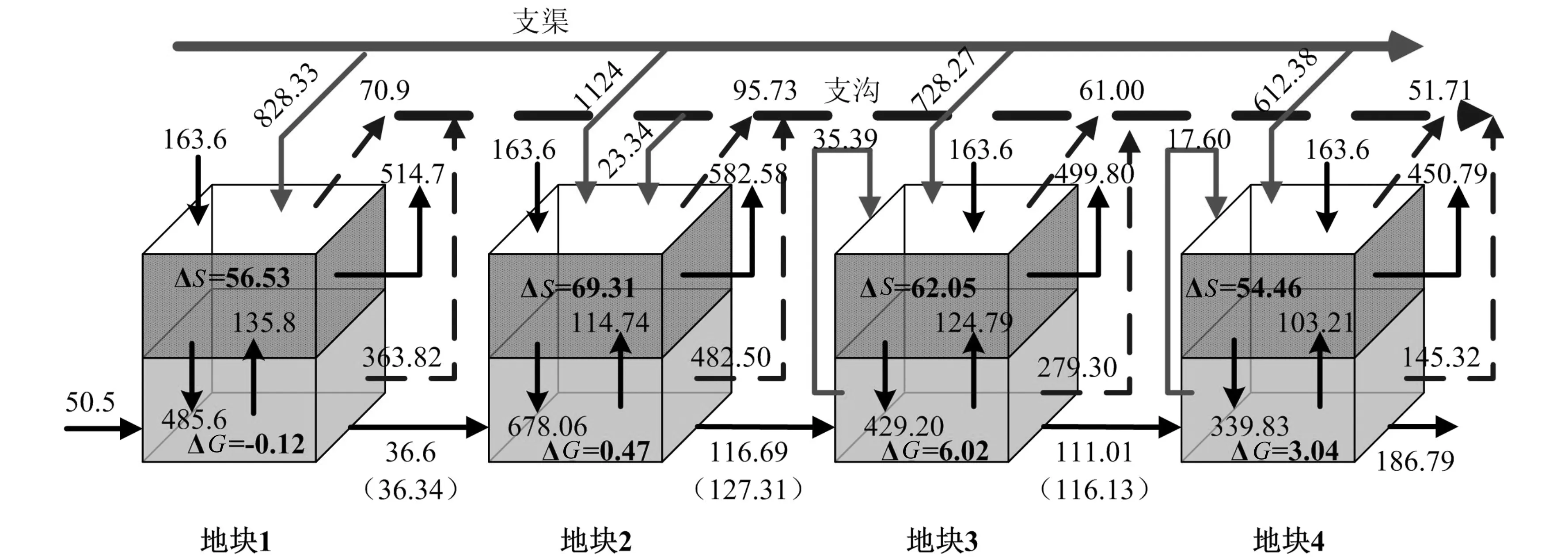
图5 研究区水均衡图(单位:mm)Fig.5 Schematic diagram of the water budget in study area

从整个研究区的角度可以更清楚的看到总体的水收支状况，图6给出了整个研究区土壤水和地下水的水分收支比例。从图6可以看出，土壤水分收入方面，渠道引水灌溉是主要的供水来源，占总水分收入的73.35%，其次为降雨量和潜水蒸发量，分别占比14.42%和10.58%，由于地下水埋深较小，地下水通过毛管上升作用进入土壤水库被作物吸收利用量较大。在水分支出方面，作物腾发量和深层渗漏量大概是1∶1的比重，地表排水量相对较小，只占6.6%。在地下水分收支方面，地下水库的水分收入主要来自渠系和田间的渗漏补给，该变量与侧向流入的比值大概8.5∶1.5；地下水库支出方面，地下水向沟道的排水量占比较大，达57.1%，主要是地下水埋深较浅导致。侧向流出量和潜水蒸发量占比接近，皆为20%左右，地下抽水灌溉量占比相对较小。

表3 不同地块水均衡框架Tab.3 Water accounting for different fields

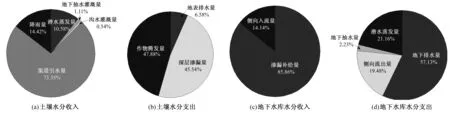
图6 研究区水分收支状况Fig.6 Water budget for the soil water and groundwater system

2.3 用水效率尺度效应

根据2.2节不同尺度灌溉用水效率计算公式以及表3中研究区水平衡要素模拟量化结果可以计算得到不同尺度灌溉用水效率评价结果。

图7为单个地块两种灌溉用水效率指标评价结果，从图7可以看出，腾发量占净入流量比例在0.456～0.540变动，出流量占净入流量比例在0.45～0.54之间变动。地块2的用水效率相对偏低，出流量比例相对偏大，主要原因在于该地块水稻所占面积相对较大，导致灌溉水量和出流量较大所致。

图7 单个地块用水效率评估Fig.7 Irrigation water use efficiency (IWUE) in different fields

图8为不同尺度灌溉用水效率评估结果。从图8可以看出，腾发量占净入流量比例总体随着尺度增大而增大，但在尺度B有所降低，主要原因在于尺度B在尺度A基础上包括了地块2，虽然该地块存在对尺度A的地表排水再利用情况(沟水灌溉水稻)，但该地块中水稻种植比例相对较大，灌溉量和出流量相对偏大，使得用水效率总体有所降低导致；随着尺度进一步增大，由于尺度C和尺度D存在对小尺度出流(地下水侧向流出)的再利用(机井抽水)，加之旱作种植面积逐渐增大，灌溉水量和出流量都有所减少，因此用水效率有所提升。出流量占净入流量比例与腾发量占净入流量比例的变化趋势正好相反，原因也在于此。

图8 灌溉用水效率尺度效应Fig.8 Scale effect of IWUE

为了尽可能削减由于种植结构空间差异导致的用水效率尺度效应，凸显重复利用水量对用水效率的作用效果，将尺度修正为单个地块-任意连续两个地块-任意连续3个地块-任意连续四个地块，并将各个尺度得到的结果进行加权平均，得到尺度修正后的灌溉用水效率随尺度变化规律，见图9。从图9看出，经过尺度修正后，用水效率随尺度发生变化规律有所改变，如腾发量占净入流量比例总体呈现单调升高趋势，从单个地块提升到连续4个地块后，该指标提升6.4%，出流量占净入流量比例总体呈现逐渐减小趋势，减小幅度6.7%。

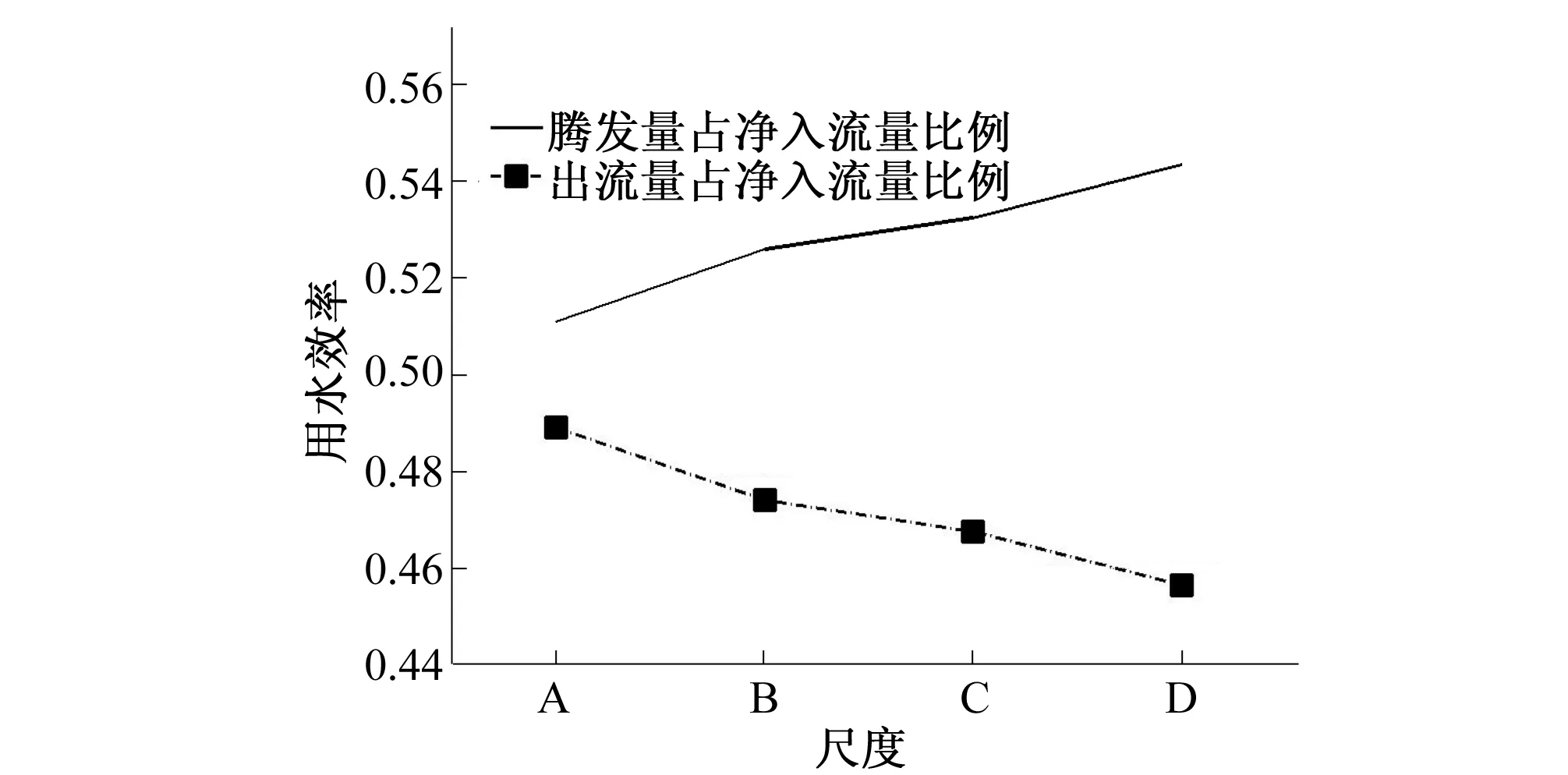
图9 不同尺度灌溉用水效率(尺度修正后)Fig.9 IWUE at multiple modified scales

3 结 语

(1)由于小尺度的出流量在更大尺度上被重复利用，不同空间范围内的灌溉用水效率表现出尺度差异性，回归水重复利用量以及种植结构等的空间差异使得灌溉用水效率的尺度效应表现显著地复杂性和非线性特征。

(2)修改后的干旱区绿洲散耗型水文模型(“四水转化”模型)可以较好的模拟宁夏惠农渠灌域典型支渠控制范围内的水分循环过程。模拟期土壤水的主要供水水源为渠道引水灌溉量，其次为降雨和潜水蒸发，主要支出为作物腾发量和深层渗漏，地表排水相对较少；地下水库的主要补给源为渠系和田间渗漏补给，主要支出是地下排水。

(3)由于存在对地表排水和地下水的重复利用，出流量占净入流量比例随着尺度的增大，总体呈现下降趋势，腾发量占净入流量比例随着尺度增大，总体呈现增大趋势；种植结构的空间差异对该尺度效应有一定负面影响，原因是尺度增大时，水稻面积有一定增加趋势，使得排水量增加，导致用水效率有一定降低。

(4)将同一尺度的多个(连续)地块进行加权平均计算灌溉用水效率，可在一定程度上减少由于种植结构空间差异对尺度效应的影响，但由于回归水重复利用量相对偏少，用水效率随尺度提升效果有限，从单个地块提升到4个地块，腾发量占净入流量比例提升6.4%。

□

[1] Hafeez MM, Bouman BAM, Van de Giesen N et al. Scale effects on water use and water productivity in a rice-based irrigation system (UPRIIS) in the Philippines[J]. Agricultural Water Management, 2007,92(1-2):81-89.

[2] 许 迪. 灌溉水文学尺度转换问题研究综述[J]. 水利学报，2006,37(2):141-149.

[3] 茆 智. 发展节水灌溉应注意的几个原则性技术问题[J]. 中国农村水利水电， 2003,(3):19-23.

[4] 陈皓锐，黄介生，伍靖伟，等. 灌溉用水效率尺度效应研究评述[J]. 水科学进展，2013,22(6):872-880.

[5] 崔远来，董 斌，李远华，等.农业灌溉节水评价指标与尺度问题[J].农业工程学报，2007,23(7):5-7.

[6] Schulze R.Transcending scales of space and time in impact studies of climate and climate change on agrohydrological responses [J].Agriculture Ecosystems and Environment，2000,82:185-212.

[7] Peter Droogers，Geoff Kite. Estimating productivity of water at different spatial scales using simulation modeling. Research Report 53[R]. Colombo，Sri Lanka：International Water Management Institute，2001.

[8] Wim Bastiaanssen，Mobin-ud-Din，Zubair Tahir. Upscaling water productivity in irrigated agriculture using remote sensing and GIS technologies[C]∥ Molden D.Water Productivity in Agriculture：Limits and Opportunities for Improvement, 37-51.CABI，Wallingford，2003.

[9] 崔远来，董 斌，李远华.水分生产率指标随空间尺度变化规律[J]. 水利学报，2006，35(1)：45-51.

[10] 陈皓锐，伍靖伟，黄介生，等.石津灌区冬小麦水分生产率的尺度效应[J]. 水科学进展，2013，24(1)：49-55.

[11] 杜丽娟，刘 钰，雷 波. 内蒙古河套灌区解放闸灌域水循环要素特征分析——基于干旱区平原绿洲耗散型水文模型[J]. 中国水利水电科学研究院学报，2011，9(3)：168-175.

[12] 雷志栋，胡和平，杨诗秀，等. 塔里木盆地绿洲耗水分析[J]. 水利学报，2006，37(12)：1 470-1 475.

[13] 黄聿刚，丛振涛，雷志栋，等. 新疆麦盖提绿洲水资源利用与耗水分析——绿洲耗散型水文模型的应用[J]. 水利学报，2005，36(9)：1 062-1 066.