基于灰色神经网络-加权马尔可夫链的大坝变形监控模型及预报研究

何 启，戴 波(1.河海大学 水利水电学院，南京 210098；2.河海大学水文水资源与水利工程科学国家重点实验室，南京 210098)

1 研究背景

近些年建成或在建的大坝规模越来越大，如二滩、向家坝、锦屏一级、溪洛渡等[1]。因此，建立大坝安全自动化监测系统，分析变形规律及时进行预报至关重要。许多学者对此进行了研究：杨杰等[2]利用误差逆传播算法的BP神经网络模型对大坝位移监测数据进行拟合及预报研究；何鲜峰等[3]对实测数据与确定性分量预测结果的残差序列进行分析，把混沌分量预报模型和分形预测模型叠加构成混合预测模型；闫滨等[4]把单纯形法嵌入遗传算法并与神经网络有机结合，构成遗传单纯形神经网络算法模型；何政翔等[5]把模糊聚类和多元逐步回归法进行结合对大坝变形资料进行分析并作出预报；此外还有多尺度小波分析的自回归预测[6]，小波消噪与BP神经网络[7]结合等预测方法。

大坝监测系统既含已知信息，又有确定、未确定的信息，因此可以把大坝看成一个灰色系统。灰色理论用于预测的模型主要是GM(1,1)，它可对时间短、数量少、波动性不大的数据序列建模，预测效果良好。BP神经网络在较大量训练样本数据的基础上才可以准确地反映非线性函数的映射关系，这在大坝蓄水初期是较难实现的。而马尔可夫链预测理论是通过状态之间的转移概率来推测系统未来发展变化的，适用于数据随机波动性较大的情况[8]。本文结合3者的优点，构建灰色神经网络-加权马尔可夫链预测模型，首先利用灰色神经网络对少量样本数据进行非线性拟合，揭示大坝水平位移的整体变化趋势，然后将其相对误差作为随机波动数据序列，利用加权马尔可夫链确定相对误差的转移概率来修正模型预测值，提高预测精度[9]。

2 灰色神经网络-加权马尔可夫链预测模型的构建

由于原始数据数量的有限性，数据本身的波动性和无序性，欲将灰色模型预测精度控制在一定范围内比较困难。神经网络需要大量数据才能取得良好的预测效果，故引入灰色理论构建灰色神经网络模型可减少对样本数量的依赖。虽然灰色神经网络模型在小样本数据预测中优于传统GM模型，但一些预测值的相对误差较大，难以满足预测要求[10]，而马氏链适用于数据波动性较大的预测问题。

2.1 GM(1，1)模型

记原始序列X(0)={x(0)(k1),x(0)(k2),…,x(0)(kn)}，x(0)≥0,k=1,2,3,…,n，X(1)为X(0)对原始数据作一次累加：

(1)

GM(1，1)模型为：

(3)

k=1,2,…,n

(4)

GM(1，1)模型预测值与实际值的相对误差为：

(5)

式(5)反应的是拟合值与原始值的偏离程度。

2.2 灰色神经网络模型

n个参数的灰色神经网络模型的微分方程表达式为：

(6)

式中：y2,…,yn为系统输入参数；y1为系统输出参数；a,b1,b2,…,bn-1为微分方程系数。

式(9)的时间响应式为：

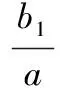
(7)

令：

式(10)可以作如下转化：

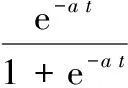
(8)

将转化后的公式用扩展的BP神经网络进行映射得到n个输入值、1个输出值。网络拓扑结构如下图1所示。

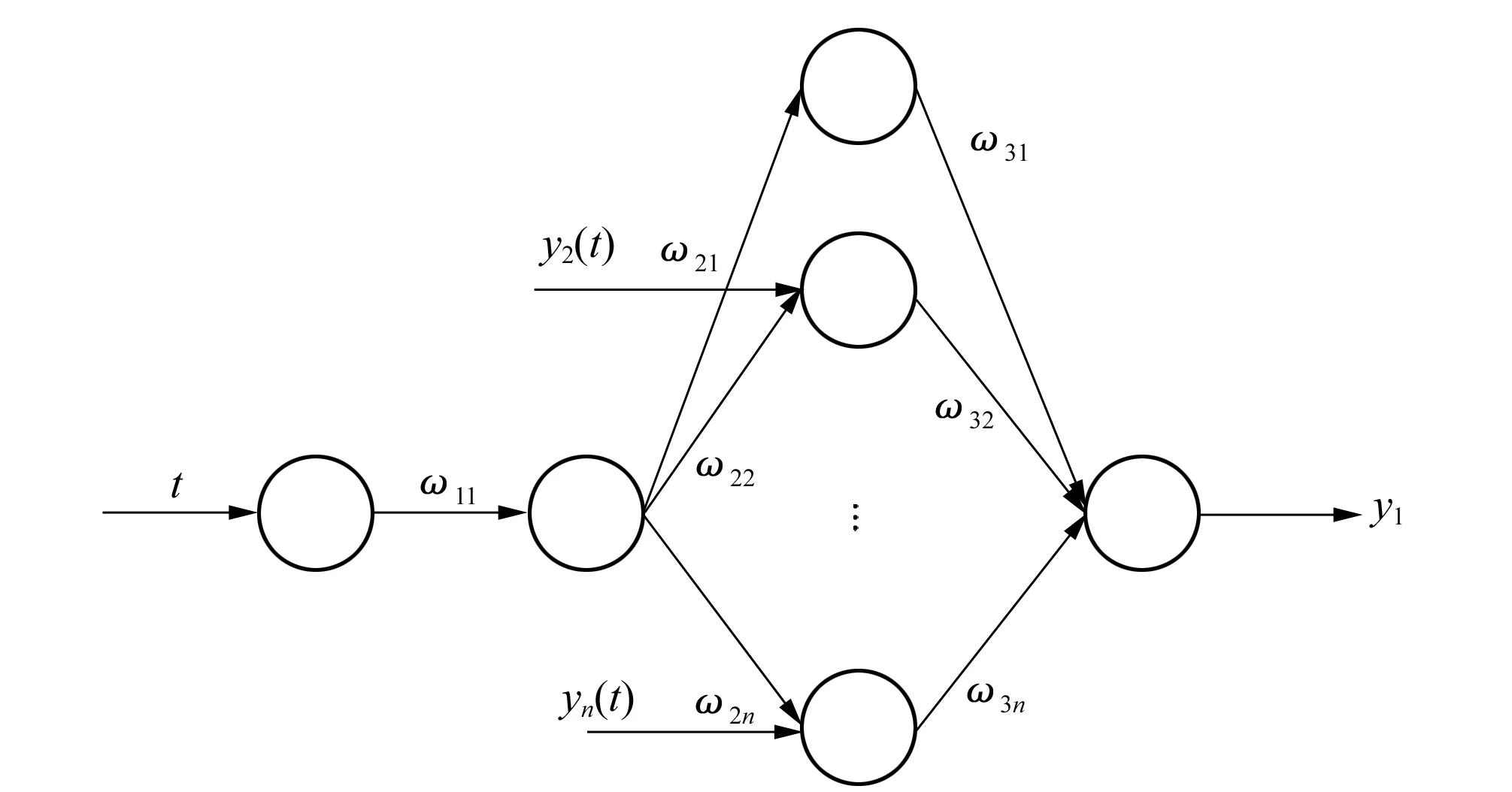
图1 灰色神经网络拓扑结构Fig.1 Grey neural network topology

图1中，t为输入参数序号；y2(t),…,yn(t)为网络输入参数；ω21,ω22,…,ω2n，ω31,ω32,…,ω3n为网络权值；y1为网络预测值。

2.3 加权马尔可夫链预测的基本步骤

根据实测资料建立训练样本，利用灰色神经网络可拟合出一条非线性函数曲线，确定大坝变形的趋势，然后利用马尔可夫链的“无后效”性分析相对误差的波动规律，修正预测值。对几种传统马尔可夫链预测方法的对比研究表明:加权马尔可夫链预测理论在数据序列随机波动性较大的预测中精度最高[11]。

根据马尔可夫链理论，首先计算灰色神经网络模型ε(k)的转移概率矩阵，然后对同一状态下的概率进行加权求和，其最大值对应的状态即为加权马尔可夫链的预测状态，并依此对灰色神经网络模型结果进行修正[12]。具体步骤如下。

(2)按(1)所建立的分级标准，确定各拟合值相对误差所对应的状态。

(3)“马氏性”检验。通常用χ2统计量来检验随机离散序列的马氏链。设所讨论的序列包含m个可能的状态，(fij)ij∈E代表状态转移频数矩阵，将(fij)ij∈E的各列之和除以各行各列的总和得到“边际概率”，记为：

(9)

(4)计算各阶自相关系数。即:

(10)

式中：rk为第k阶自相关系数；xl为第l时段的相对误差；n表示相对误差序列长度。

对各阶相关系数规范化：

(11)

作为各种步长的马尔可夫链的权重。

p(K)=(p(K)ij)ij∈E

(12)

(6)以离预测值最近的K个相对误差值为初始状态，根据其相应的转移概率矩阵即可预测该时段相对误差的状态概率p(K)i,i∈E,K为步长，K=1,2,…,m。

(7)确定预测状态。对同一状态的各预测概率进行加权求和，得到相对误差的转移概率为：

(13)

max{pi,i∈E}所对应的状态为该时段相对误差的预测状态。

(8)利用状态特征值结合线性插值的方法对预测值进行推断[13]， 先计算状态特征值：

(14)

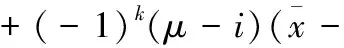
(15)

也可用上限法：

x)

(17)

(9)对后续时间预测，将前一时间预测值加入原序列中重新构置马尔可夫链，重复步骤(1)～(8)可进行预测。

3 实例分析

某水电站大坝为碾压混凝土重力坝，位于福建省境内，该工程除发电外，在防洪、航运、水产养殖等方面也发挥着效益。水电站建成后，是闽西南最大水电站，也是省网主要电源之一，可以担任省网调峰、调频任务，同时对增加网内有调节能力的水电比重发挥作用，改善了省网电源北重南轻布局。

3.1 预测因子的选择与处理

为加快学习的速度，可对训练样本数据按如下公式进行归一化处理：

X′=0.1+0.8 (X-Xmin)/(Xmax-Xmin)

(18)

式中：Xmax、Xmin分别表示每组样本数据的最大、最小值。

3.2 灰色神经网络的大坝变形预测结果

根据4号坝段PL7正垂线 方向(上下游方向为正)位移监测资料建立灰色神经网络模型。选取蓄水初期2003年11月14日至2003年12月20日的实测数据作为训练样本用于拟合计算，共37组，取12月20-26日6组数据作为预测样本，评价模型的预测性能。

根据原数据序列建立灰色神经网络模型并运用Matlab程序训练、预测，预测结果如表1所示。

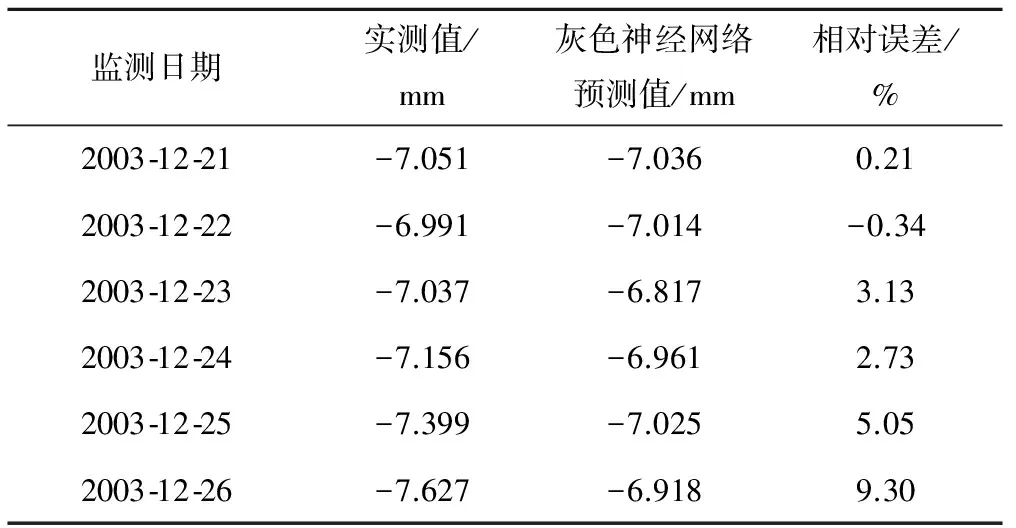
表1 水平位移预测结果与实测值的相对误差Tab.1 Prediction of horizontal displacement and the relative error of the measured value

从表1中可以看出，灰色神经网络适应于小样本预测，但某些相对误差相对较大，因此可用加权马尔科夫链理论对结果进行进一步修正。

3.3 加权马尔可夫链拟合及预测结果

(2)根据状态区间确定各拟合值相对误差对应的状态如表2中“5”纵栏所示。

表2 灰色神经网络预测结果、相对误差及状态Tab.2 Grey neural network predicting, relative residuals and states

(3)不妨直接对37组相对误差作马氏性检验，根据步骤(5)和表2的资料可计算进一步状态转移频数矩阵和一步转移概率矩阵：

(4)根据步骤(4)计算各阶自相关系数，如表3所示。

(5)根据步骤(5)计算相对误差的K步状态转移概率矩阵p(K)：

表3 各阶自相关系数和各种步长的马尔可夫链权重Tab.3 The weights of Markov chain of various steps and various auto-relative coefficients

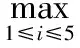
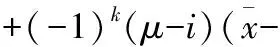
同理，将计算出的预测值加入原序列中重新构置马尔可夫链，重复过程 (1)-(7)计算得2003年12月22日-2003年12月26日的预测值，相对误差范围为0.055%～1.625%，精度较高。本文又采用GM(1,1)模型进行对比预测，结果见表5和图2。

表4 2003-12-21水平位移状态预测Tab.4 Prediction of horizontal displacement state on 2003-12-21

表5 不同模型预测结果比较Tab.5 Comparison of the results of different prediction model

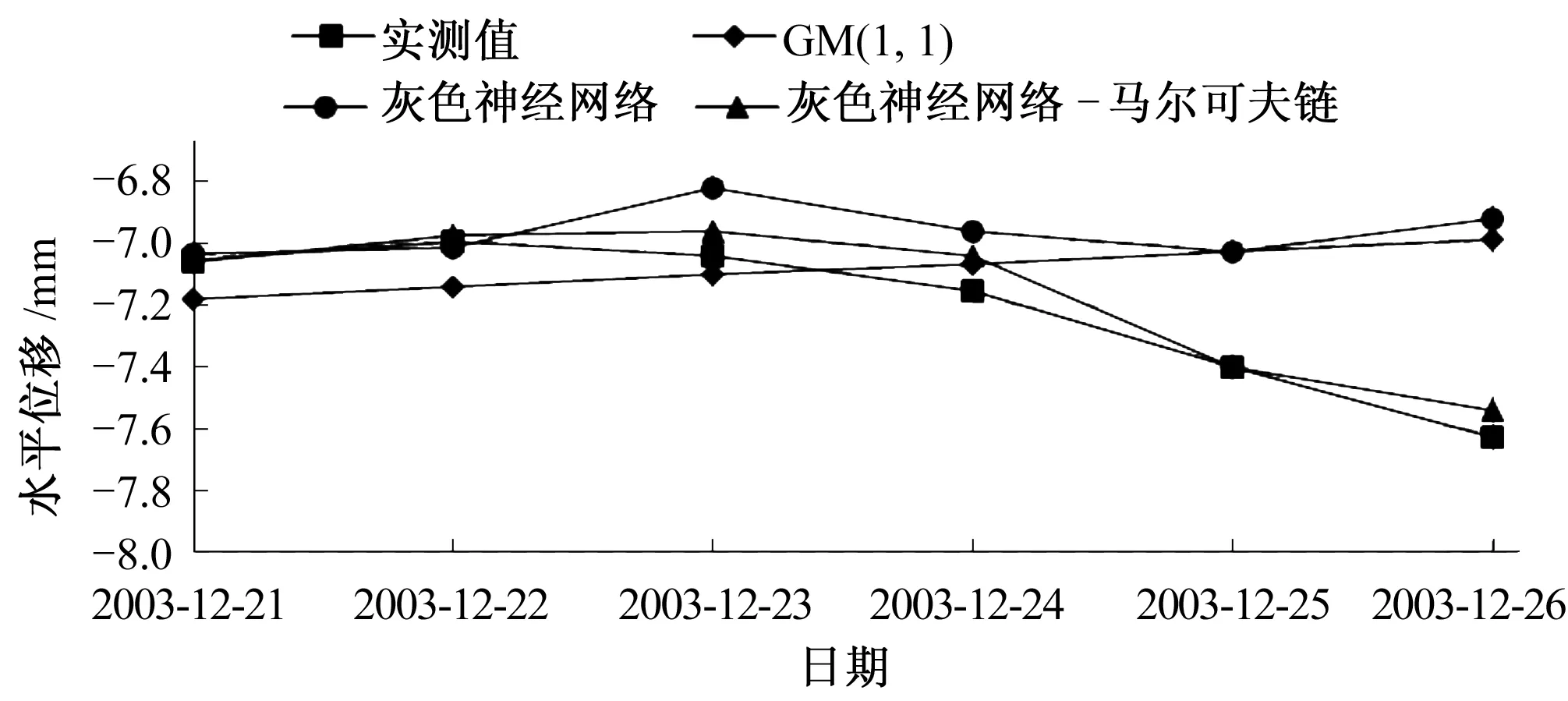
图2 不同模型预测结果比较Fig.2 Comparison of the results of different prediction model

通过对比3种方法的预测结果，可知灰色神经网络-加权马尔可夫链模型的预测误差显著降低，实测值与预报值更为接近，预测精度优于其他两种模型，为小样本、波动性大的数据预测提供了新的方法参考。

4 结 语

本文针对蓄水初期阶段大坝监测数据有限且波动性大的特点，结合灰色理论适应于小样本、BP神经网络高效准确拟合非线性函数、马尔可夫链适应于波动性比较大数据的优点，建立了灰色神经网络-加权马尔可夫链模型。通过某碾压混凝土坝4号坝段蓄水初期水平位移监测资料进行预测，结果表明该模型对小样本、数据序列波动大进行预测精度较高。由本文还可得到如下结论。

(1)灰色神经网络-加权马尔可夫链模型不仅可对大坝变形进行短期高精度预报，随着监测数据的增加也可为中长期预报提供理论方法。

(2)在完成一步预测后，将预测信息重新加入原模型进行下一步预测，可对资料数据进行动态更新，跟踪大坝变形的发展变化趋势，也提高了预测精度。

□

[1] 吴中如.水工建筑物安全监控理论及其应用[M].南京:河海大学出版社,1990.

[2] 杨 杰,吴中如,顾冲时，等.大坝变形监测的BP网络模型与预报研究[J].西安理工大学学报,2001,17(1):25-29.

[3] 何鲜峰,顾冲时,谷艳昌，等.分形-混沌混合预测模型在大坝安全监测中的应用[J].武汉大学学报(工学版),2008,41(1):45-49.

[4] 闰 滨,周 晶.基于遗传单纯形神经网络的大坝变形监控模型[J].水力发电学报,2007,26(4):110-114.

[5] 何政翔,张慧莉.模糊聚类方法应用于大坝变形监测资料分析[J].水力发电,2013,(11):59-61.

[6] 徐 伟,何金平.基于多尺度小波分析的大坝变形自回归预测模型[J].武汉大学学报(工学版),2012,45(3):286-289.

[7] 黄世秀,洪天求,高 飞，等.基于小波消噪及BP神经网络的大坝变形分析[J].人民长江,2011,42(9):90-93.

[8] 杜 川,梁秀娟,王中凯，等.改进灰色-马尔科夫模型在年降水量预测中的应用研究[J].节水灌溉,2014,(6):32-36.

[9] 杨皓翔,梁 川.基于加权灰色一马尔可夫链模型的城市需水预测[J].长江科学院院报,2015,32(7):15-21.

[10] 薛鹏松,冯民权,邢肖鹏.基于马尔科夫链改进灰色神经网络的水质预测模型[J].武汉大学学报(工学版),2012,45(3) 319-324.

[11] 夏乐天,朱元牲.马尔可夫链预测方法的统计试验研究[J].水利学报,2007,10(增):372-378.

[12] 赵 玲,许宏科.基于灰色加权马尔可夫SCGM(1,1)的交通事故预测[J].计算机工程与应用,2012,48(31):11-15.

[13] 夏乐天.马尔可夫链预测方法及其在水文序列中的应用研究[D].南京：河海大学,2005.

[14] 顾冲时,吴中如.碾压混凝土坝安全诊断与预警的理论和方法[M].南京:河海大学出版社，2012.