基于GA优化AR-LSSVR组合模型在区域降雨量预测中的应用研究

丁星臣，徐淑琴，路豪杰，陈际旭，刘琦峰

(东北农业大学水利与建筑学院，哈尔滨 150030)

目前降雨量的预测方法主要有小波神经网络法[1]、序位集对分析法[2]、均生函数法[3]、时间序列法[4]、马尔科夫预测法[5]、贝叶斯概率预报[6]、支持向量机预测法[7]等，而实际的降雨量数据并非纯粹呈指数的增长规律，是一种具有剧烈波动的非线性变化规律，利用单一的预测方法虽然在预测过程中取得了较好的效果，但自身难免都存在一些不足，单独使用预测精度不是很理想，误差较大。比如时间序列法在数据波动较大时预测效果较差，人工神经网络存在局部收敛、过拟合、网络层数和各层神经元数没有统一的确定标准等问题[8]，最小二乘支持向量机(Least Square Support Vector Machines，LS-SVM)继承了标准SVM优异的泛化性能和全局收敛能力，用等式约束代替了不等式约束，并用训练误差的平方代替了松弛变量，从而优化了SVM复杂的运算过程，极大地提高了训练速率[9]。本文针对目前降雨量预测方法存在的不足提出时间序列最小二乘支持向量机组合模型的降雨量预测方法，该组合模型充分考虑了降雨量变化的时序动态性、随机性因素，提高了预测准确度，为地区降雨量的精确预报提供了一种新的方法。

1 降雨量时间序列模型的构建

1.1 模型的基本原理

时间序列分析是一种暂不考虑外界因素影响对动态数据处理的统计方法，对非线性数据具有较好的拟合效果，本文首先对858农场1963-2004年的年降雨量采用AR模型进行拟合，年降雨量动态变化组成的数学表达式如下：

H(t)=h(t)+v(t)+x(t),t=1,2,3,…,n

(1)

式中:H(t)为年降雨总量，mm；h(t)为趋势变化项，mm；v(t)为周期变化项，mm；x(t)为随机干扰项。

1.2 模型各分量的确定

1.2.1趋势变化项h(t)

利用Excel2010软件数据回归分析功能对原始数据添加趋势线，在α=0.05显著水平下，挑选出适宜的趋势项模型为：

h(t)=0.086x2-5.006x+602.5,r2=0.028

(2)

由于降雨量数据动态变化趋势呈现较明显的周期性变化特点，本文采用谐波分析法提取周期项，取倍频极限即最大波数p=(N/2)，N为样本数，N=42，则p=21。根据最小二乘法和三角函数的正交性，可以得到序列v(t)的谐波系数估计值即傅立叶系数。在α=0.05显著水平下，Fα=3.05，经过对各个谐波方差进行检验，达到显著水平的谐波只有24号，其对应的F统计量为3.448 5>Fα=3.05。达到显著水平。故提取第24号谐波建立的周期序列为：

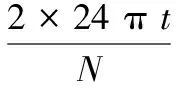
(3)

1.2.3随机干扰项x(t)

假定降雨量随机成分x(t)为平稳的，则x(t)由平稳相依成分D(t)和平稳独立随机成分(纯随机成分)εt组成，即x(t)=ε(t)+D(t)。对于x(t)可以用线性平稳随机模型来表示他的统计特征。一般的自回归模型表示为：

(4)

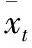
首先对序列x(t)分别进行自相关分析和偏相关分析[10]，自相关图和偏相关图如图1、图2所示。

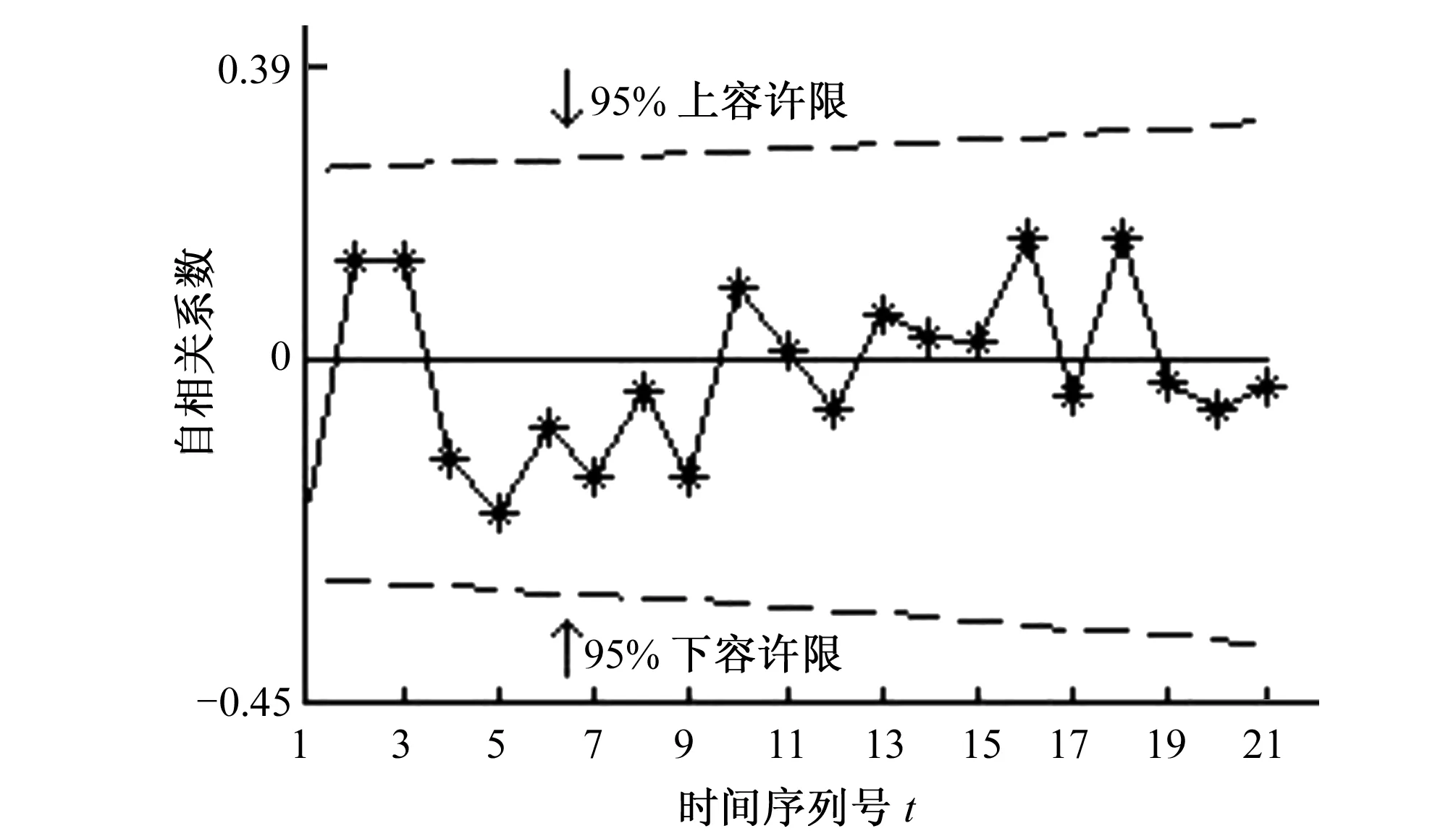
图1 自相关图Fig.1 Auto correlation graph

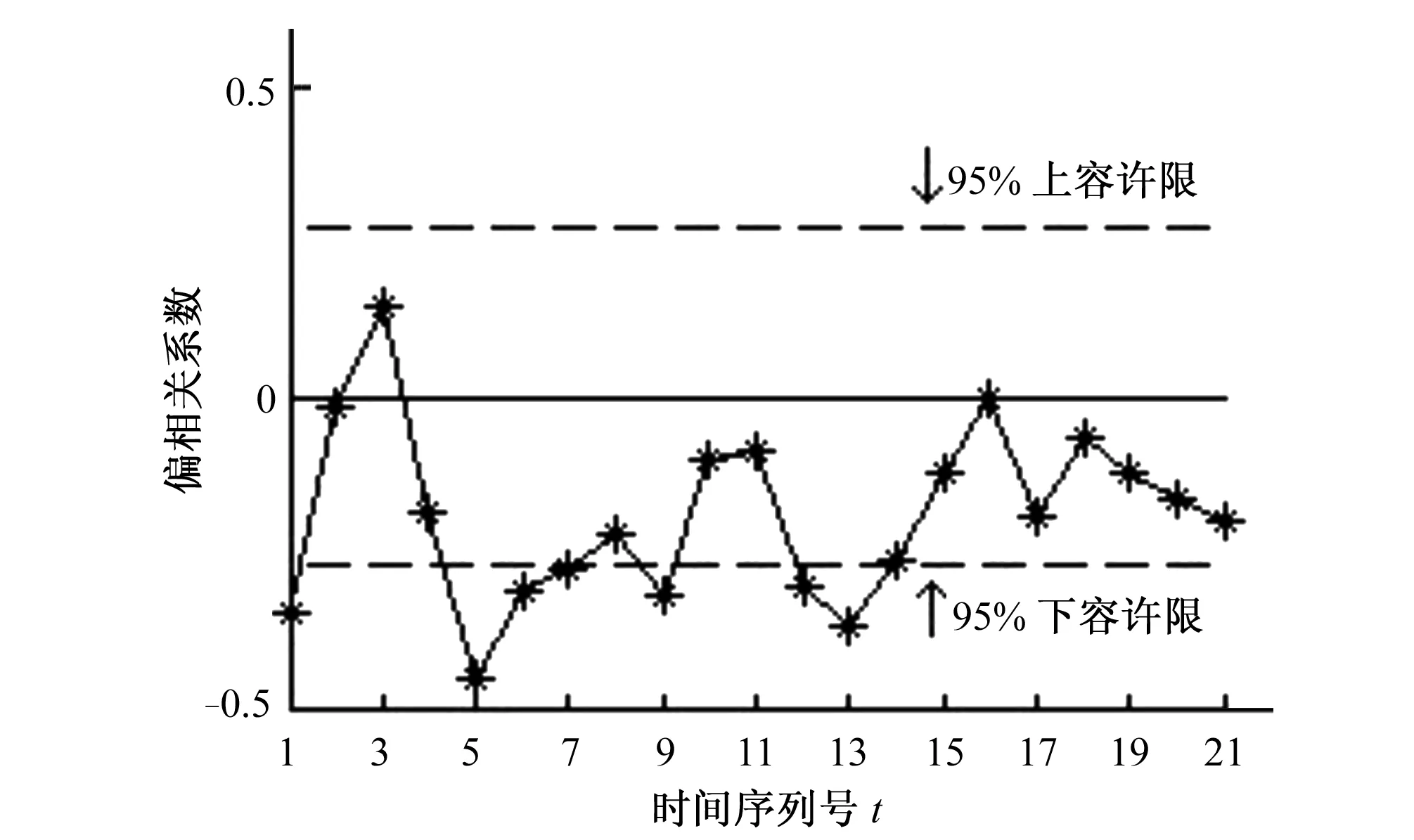
图2 偏相关图Fig.2 Partial correlation graph

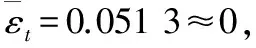
退行性膝关节骨性关节炎主要发生群体是老年人,随着国家老龄化社会结构的到来,退行性膝关节骨性关节炎的发生率逐年上升,该病症会严重影响患者的生活质量,甚至对社会生产力造成一定程度影响。退行性膝关节骨性关节炎会致使患者有巨大的病症疼痛感,也是致使患者残疾的重要原因之一。本文对退行性膝关节骨性关节炎患者的治疗过程中应用刺络放血配合温针灸治疗,以此评价刺络放血配合温针灸治疗的效果及对VAS评分的影响。

1.3 降雨量时序模型的建立

将以上计算得到的趋势项h(t)、周期项v(t)及随机性干扰项x(t)进行叠加，得到降雨量非平稳时序随机模型。应用该模型对858农场年降雨量拟合结果见图3。

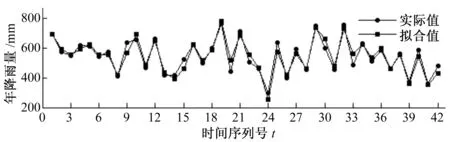
图3 1963-2004年降雨量拟合图Fig.3 1963-2004 annual rainfall fitting

2 最小二乘支持向量机的基本理论

根据Suykens的LS-SVM理论，LS-SVR建模的主要思想是首先把一训练样本集：(xi,yi),i=1,2,…,n,x∈Rd,y∈R通过非线性函数φ(x)将样本从原输入空间Rd映射到一个高维的特征空间Z中，在特征空间，采用如下公式来估计未知的非线性函数：

y=wTφ(x)+b

(5)

式中：φ(x)为空间映射函数；w为权重向量；b为偏置。

按结构风险最小化原理，LS-SVR取逼近误差二次项和来控制模型的经验风险，其优化问题被定义为：

(6)

式中：γ为正则化参数。

为求解上一优化问题，构造拉格朗日函数如下：

(7)

式中：αi∈R(i=1,2,…,N)为Lagrange因子。

根据最优性条件，分别求L关于变量(w,b,ei,αi)的偏微分，得到：

(8)

方程组(8)中，消去变量w和ei，再利用Mercer条件：

Ωi,j=φ(xi)Tφ(xj)=K(xi,xj),i,j=1,…,N

(9)

得到矩阵形式为：

LS-SVR模型的表达式为：

(10)

式中：αi,b是方程组(8)的解[11-14]。

3 AR-LSSVR组合模型在858农场年降雨量预测中的应用

本文选取858农场1963-2004年降雨量作为训练集，2005-2014年降雨量作为测试集，并对2015-2017年降雨量进行预测。首先采用AR模型对数据进行拟合，拟合结果见前文图3，用实际值与拟合值计算42个时间点对应的绝对误差，见图4。

图4 绝对误差分布图Fig.4 Absolute error distribution

从图4中可以看出，绝对误差数值分布规律具有很强的周期性，可以很好地用LS-SVR进行拟合，本文采用径向基核函数(RBF)：

RBF的参数较少，且变量限制性条件少，可以降低模型的复杂性，提高模型的训练速度。影响LS-SVM训练效果主要的参数是惩罚参数c和核函数参数g，惩罚参数和核函数参数是需要在模型训练前事先假定的，它决定了模型拟合的效果和预测精度，若c取值较小，则对样本数据的离群点惩罚度减小，使训练精度变差，算法的泛化能力加强。若c取值较大，相对应的wTw/2就小，算法的泛化能力将会变差。核函数参数g太小会对样本数据造成过学习现象，太大会对样本数据造成欠学习现象。本文采用交叉验证方法寻找最佳的惩罚参数c和核函数参数g，将原始数据均分成7组，将每个子集数据分别做一次验证集，同时其余的6组子集数据作为训练集，这样会得到7个模型，用这7个模型最终的验证集分类准确率的平均数作为此K-CV下分类器的性能指标，在每个模型最优参数选定过程中，本文采用遗传算法对参数进行寻优，避免了传统的网络搜索法在大范围寻优费时等缺点，采用启发式算法可以不必对网络内的所有参数点计算其分类准确率，迅速找到全局最优解，参数寻优的算法流程见图5。

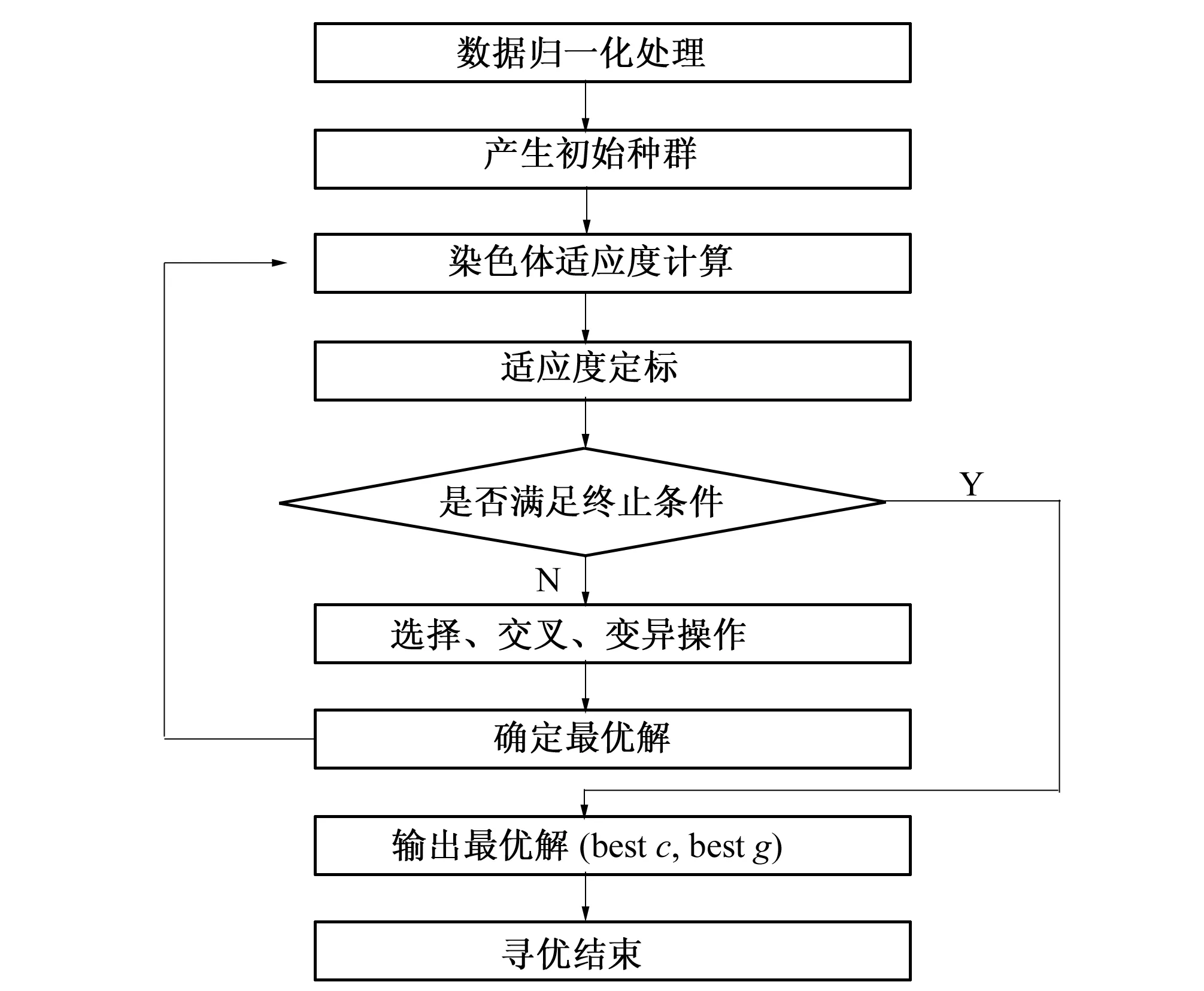
图5 GA优化流程图Fig.5 GA optimization flow chart

本文首先对绝对误差做归一化处理，最大进化代数为500，种群最大数量为20，参数c的变化范围设为(0，100]，g的变化范围设为[0，1 000]，交配概率及变异概率设为0.9，适应度函数采用平均相对百分比误差MAPE函数：

(11)

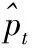
利用GA算法对训练样本寻优得到的参数c=4.066 6，g=56.968 6。组合模型的预测原理如图6所示。

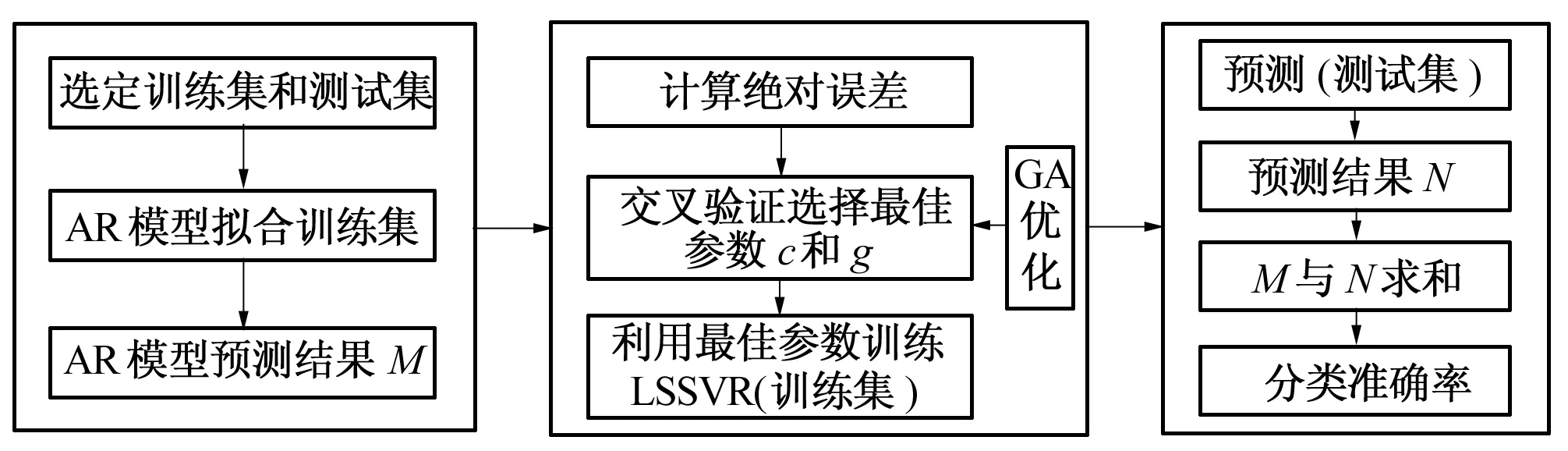
图6 AR-LSSVR组合模型预测原理Fig.6 AR-LSSVR combination model prediction principle

为了说明模型预测的准确性，利用组合模型对2005-2014年降雨量进行预测，预测结果见图7，将预测值与实际值作比较，得到相对误差分布图见图8。

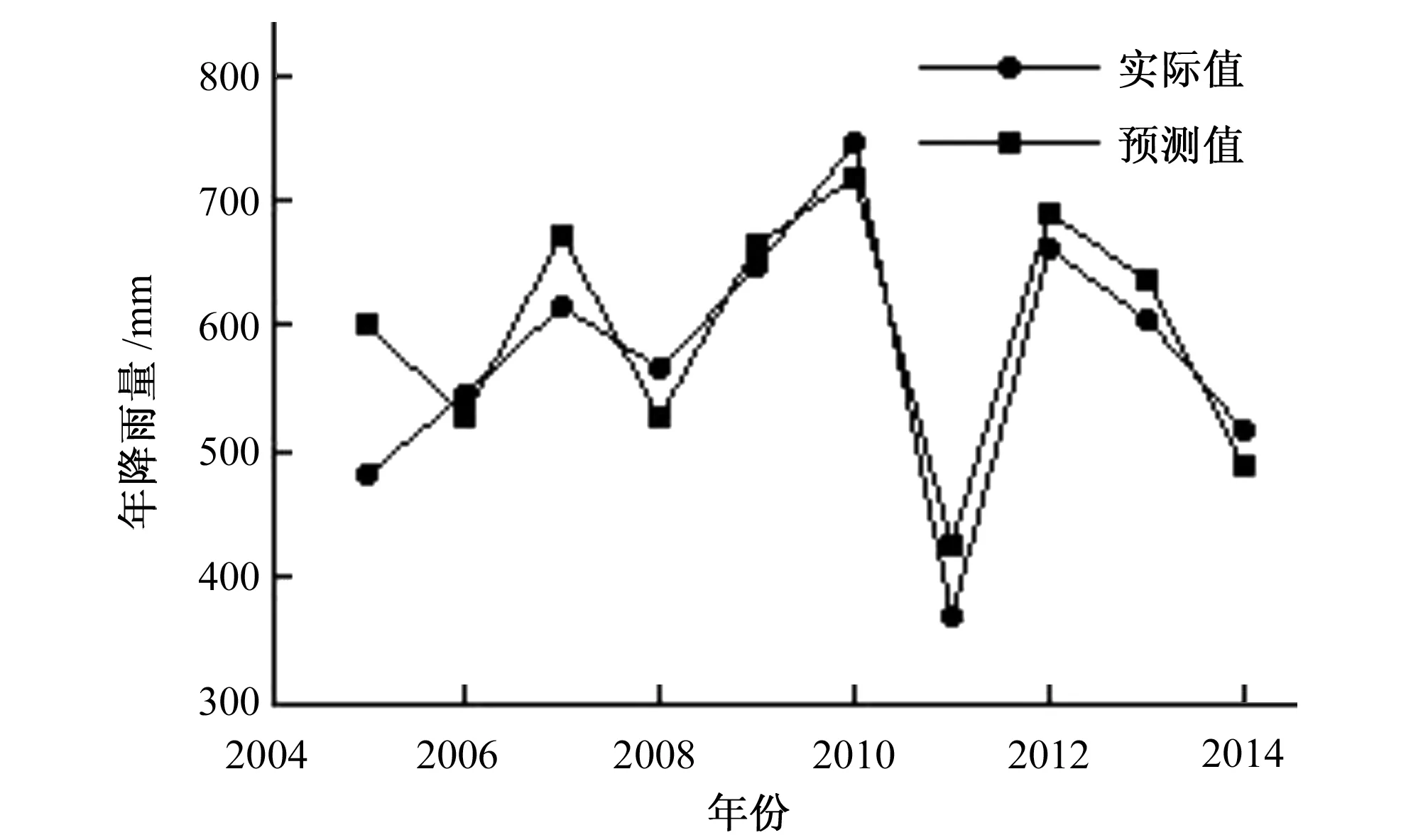
图7 2005-2014年降雨量预测值Fig.7 2005-2014 annual rainfall forecast

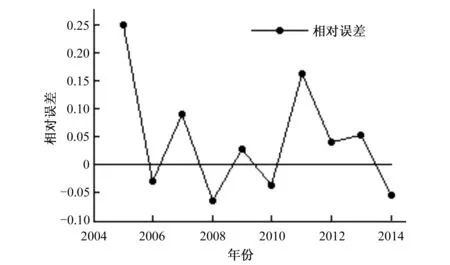
图8 相对误差分布Fig.8 Relative error distribution

由相对误差分布图可看出，2004和2011年的预测误差较大，其他年份误差较平稳，误差较小，根据《水文情报预报规范》[15]，相对误差≤20%为合理的预测标准，经过计算，本文预测检验合格率大于20%的达到了90%，达到一级预测标准。因此所建立的858农场AR-LSSVR组合预测模型具有较好的可靠性和预测精度，可以对858农场未来的降雨量进行预测。现对858农场2015-2017年的年降雨量进行预测，预测结果见表1。

表1 2015-2017年降雨量预测值 mm

4 结论与讨论

本文针对如何提高年降雨量预测精度提出AR与LSSVR组合模型，AR模型对非平稳降雨量数据进行预测时，由于不能消除其波动性使预测效果不理想，LSSVR的训练过程等价于求解一个线性且有限制性条件的二次规划问题，具有泛化能力强、不易陷入局部极小等优点，较好地解决了小样本、非线性、高维数、和局部极小问题，改进的GA优化算法能够在大范围快速准确地寻找最佳的核函数参数g和惩罚参数c，提高了LSSVR对样本的训练效果以及预测精度，为降雨量预测提供了一种快速的参数寻优方法。

虽然该模型达到了较高的预测精度，但还可以做更深入的研究：①影响降雨量的因素很多，本文由于数据的限制，仅采用单一年降雨量数据进行预测还不够全面，如果能同时考虑日照时间、空气湿度、大气中水气含量、地面蒸发量、风速等因素，能够提高降雨量的预测精度。②支持向量是SVM的训练结果,在SVM预测过程中起决定作用的是支持向量，而本文LSSVR训练过程中，将所有训练样本作为支持向量，降低了支持向量机的稀疏性，如能提出一种新的改进算法，可以提高LSSVR训练的准确性和运算速率。

[1] 侯泽宇,卢文喜,陈社明. 基于小波神经网络方法的降水量预测研究[J]. 节水灌溉,2013,(3):31-34.

[2] 刘银迪,张小壮,张泽中. 序位集对分析在辽河流域年降雨预测中的应用[J]. 安徽农业科学,2011,28:17 534-17 536.

[3] 窦浩洋,邓 航,孙小明,等. 基于均生函数-最优子集回归预测模型的青藏高原气温和降水短期预测[J]. 北京大学学报(自然科学版),2010,(4):643-648.

[4] 刘 杨,徐淑琴,董丽丽,等. 时间序列模型在查哈阳农场降雨量预测中应用[J]. 黑龙江水利科技,2012,(2):5-7.

[5] 杜 川,梁秀娟,王中凯,等. 改进灰色-马尔科夫模型在年降水量预测中的应用研究[J]. 节水灌溉,2014,(6):32-36.

[6] 邢贞相. 确定性水文模型的贝叶斯概率预报方法研究[D]. 南京：河海大学,2007.

[7] 欧阳琦,卢文喜,董海彪,等. 基于支持向量机回归分析的降水量预测研究[J]. 节水灌溉,2014,(9):38-41.

[8] 白玉洁. 改进时间序列模型在降雨量预测中的应用研究[J]. 计算机仿真,2011,(10):141-145.

[9] 李丽娟. 最小二乘支持向量机建模及预测控制算法研究[D]. 杭州：浙江大学,2008.

[10] 付 强.数据处理方法及其农业应用[M]. 北京：科学出版社, 2006:430-433.

[11] 曾 杰,张 华. 基于最小二乘支持向量机的风速预测模型[J]. 电网技术,2009,(18):144-147.

[12] 姜静清. 最小二乘支持向量机算法及应用研究[D]. 长春：吉林大学,2007.

[13] 袁从贵. 最小二乘支持向量回归及其在水质预测中的应用研究[D]. 广州：广东工业大学,2012.

[14] 陈其松. 智能优化支持向量机预测算法及应用研究[D]. 贵阳：贵州大学,2009.

[15] GB/T 22482-2008，水文情报预报规范[S].