面向生态的黑河中游模糊多目标水资源优化配置模型

杨献献，郭 萍，李 茉

(中国农业大学水利与土木工程学院，北京 100083)

流域水资源优化配置是在水资源生态经济复合系统内，按照可持续性、有效性、公平性和系统性的原则，遵循生态规律和经济规律，对特定流域内不同形式的水资源，通过各种工程和非工程措施，以单位产值的水资源消耗最小，生态系统提供的服务最大为目标，在生态与社会经济用水之间、区域之间、经济用水部门之间进行科学调配，尽可能提高流域整体的用水效率，促进流域水资源的可持续利用、生态系统的健康稳定和区域的可持续发展[1]。由此可见，研究水资源优化配置必须将生态用水纳入体系。考虑生态需水的水资源优化配置的研究，一方面是将生态需水作为约束[2-4]或生态目标[1]；另一方面是将生态服务价值引入模型[5]，综合考虑用水效率。然而，生态服务价值是一个比较模糊的数值，国内外虽然都给出了量化的方法，但是不同的专家对生态价值的评估差异很大，还没有系统的能让专家达成共识的体系。而且单位面积上的生态系统服务价值是一个不断变化的值，它会随着研究的深入、评估更广泛的生态系统服务、生态动力学和相互依存更实际地结合、生态系统服务功能变得更紧张而增长[6]。所以，将不确定性引入生态服务价值的估计很有必要，目前还没有发现类似的研究。

黑河中游位于黑河干流上的莺落峡和正义峡之间，从行政区来看，黑河中游包括张掖市的甘州区、临泽县和高台县。该区光热资源丰富，但干旱严重，依靠黑河供水，人工绿洲发育，是甘肃省的重要农业区。根据《黑河流域综合规划(东部子水系)》，全区用水总量17.24 亿m3，其中，农田灌溉用水达到14.62 亿m3，占84.8%，人工生态用水为1.56 亿m3，仅占9.0%。为了保证生态需水，本文从生态服务价值和生态需水出发，分别建立了基于0-1整数规划的单目标和多目标不确定性水资源优化配置模型。

1 水资源优化配置模型

1.1 水资源优化配置模型系统

本文面向生态的水资源优化配置模型包括生态服务价值计算模型、生态需水计算模型、基于节水灌溉的种植面积调整模型、模糊单目标水资源优化配置模型和模糊多目标水资源优化配置模型(见图1)。研究区域水资源优化配置的目的是降低农业用水，保证生态需水。

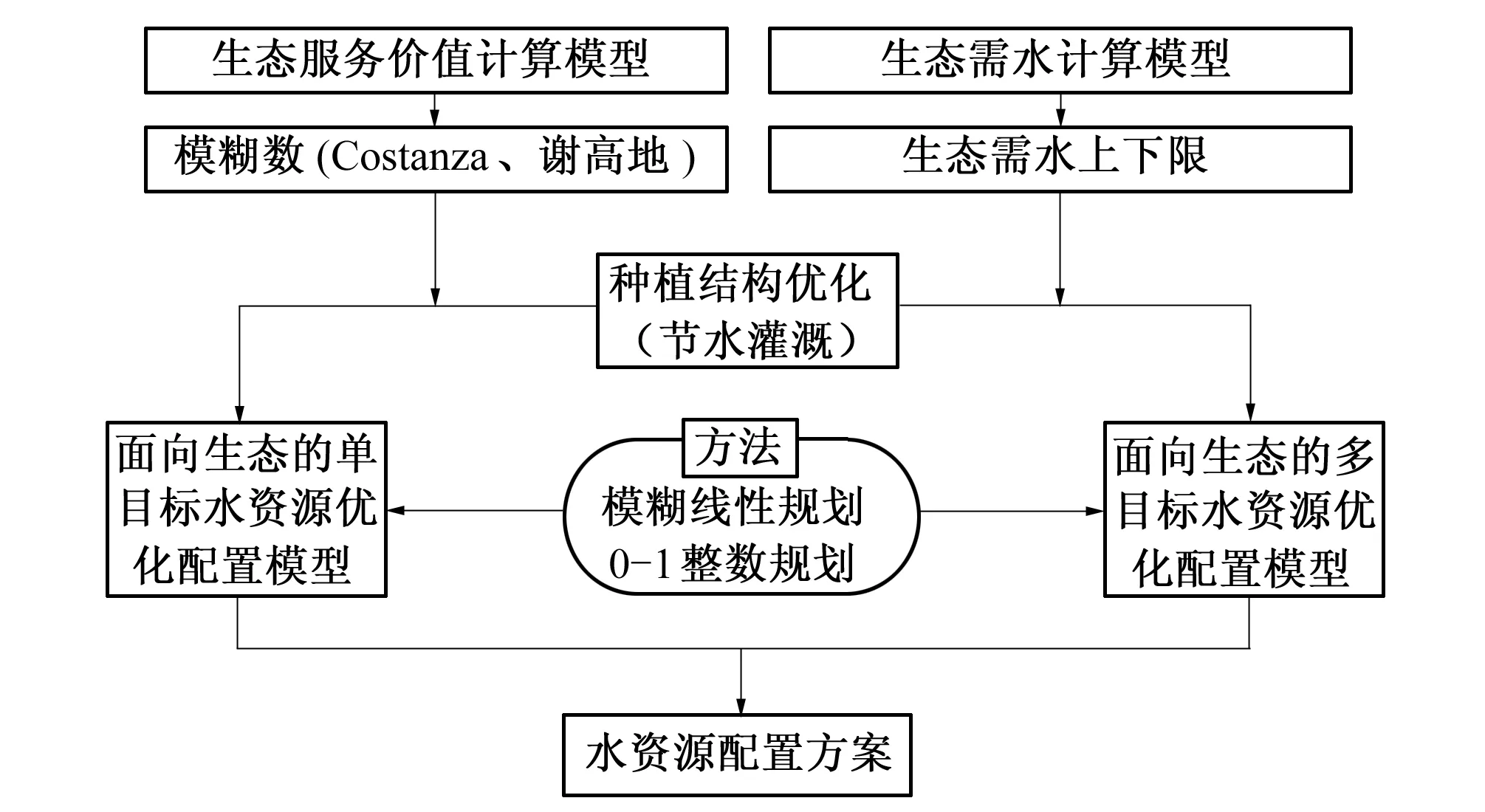
图1 水资源优化配置模型系统

1.2 方法介绍

1.2.1模糊线性规划

模糊数能够表达自然界一些属性的不确定性，将目标函数和约束条件中相关的参数用模糊数表示更具有合理性[7]。同时，约束条件也可以表示为模糊不等式约束。表示形式如下[8]：

(1)

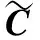
1.2.20-1整数规划

线性规划问题中，常要求某些变量的解必须是整数[9]。整数规划的一种特殊情形是0-1规划，它的变量仅限于0或1，变量以“0”表示“非”，以“1”表示“是”，0-1整数规划的一般形式如下：

(2)

式中：C为r×n目标矩阵；A为m×n约束矩阵；b为一个右边系数的m维矩阵；z为n维0-1决策变量。

1.3 单目标模糊规划水资源优化配置模型

以研究区域的农业效益和生态效益最大为目标，目标函数如下：

(5)

约束条件如下。

(1)水量约束：

(6)

式中：Q为农业和生态可利用水量，由预测得到。

(2)生态需水约束：

EWLi≤ESWi≤EWUi

(7)

式中：EWLi、EWUi分别为第i个行政区最低和最高生态需水量，根据研究区域现状结合生态需水模型[15]计算得到。具体计算内容及方法如下：采用降水蒸发差法计算水域需水；根据城镇绿化率得到各行政区绿化面积，采用定额法计算其需水量；将防护林的需水定额划分为死亡限需水、适宜需水和最适宜需水，计算其最高和最低需水量；根据2005年张掖土地利用类型图，在ARCGIS获得不同天然植被面积，采用潜水蒸发法----阿维扬诺夫公式计算天然植被需水量。各植被类型实际地下水位的确定主要有2个参考：一是根据张掖市2004年地下水埋深采用IDW空间插值得到的地下水埋深分布图；二是生态水位，即植被正常生长地下水埋深。

(3)粮食安全约束 ：

(8)

式中：TDFOOD为研究区域每年粮食总需求量，kg，由预测人口和每年人均粮食需求(420 kg)计算得到。

(4)决策变量约束：

且γijk=0或1

(9)

1.4 多目标模糊规划水资源优化配置模型

多目标水资源优化配置模型包括生态目标和经济目标，其中，生态目标以生态供水满足度最大为指标；经济目标以农业效益最大为指标，具体目标函数如下。

(1)生态目标：

(10)

式中：d为当整个研究区域生态供水量为满足生态需水下限时的满足度，一般可取0.5[1]。

(2)经济目标：

(11)

模糊多目标水资源优化配置模型中其他参数意义及约束条件同单目标水资源优化配置模型。

1.5 求解算法

(1)模糊单目标水资源优化配置模型求解算法：

第1步。将模糊单目标模型转化成如下多目标模型。

(13)

式中：TBL、TBM和TBR分别表示模糊数的下限、主值和上限；其他类似参数意义相同。

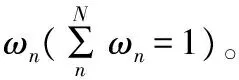
Maxf=ω1TBL+ω2TBM+ω3TBR

(14)

s.t.式(13)

(2)模糊多目标水资源优化配置模型求解算法。

第1步。将多目标模糊规划模型转化为如下多目标规划问题：

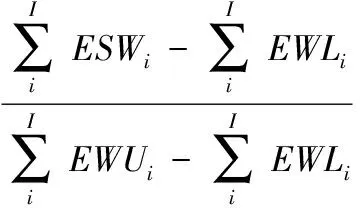
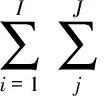
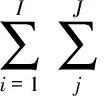
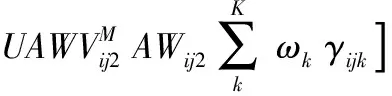
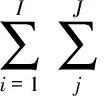
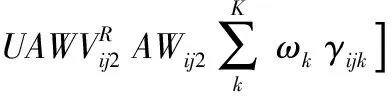
s.t.式(13)

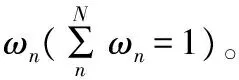
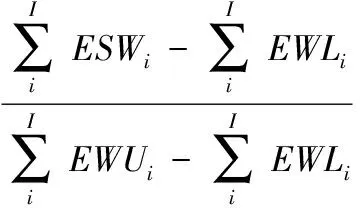
Maxf2=ω1TBL+ω2TBM+ω3TBR

(16)

s.t. 式(13)

第3步。求解如下规划问题：

Maxf*1=Maxft,t=1,2

(17)

s.t.式(13)

第4步。用标准化方法处理多维决策目标：

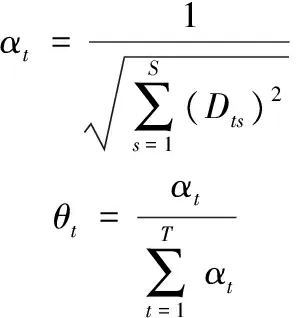
(18)

式中：Dts(t=1,2；s=1,2,…,S)是f1、f2的参数。

第5步。引入辅助变量λ，模型可以转化为如下问题：

Minλ

(20)

2 实例应用

2.1 基础数据

本文研究区域为甘州区、临泽县和高台县3个行政区，种植的农作物主要有15种，包括小麦、大麦、夏杂等。传统灌溉水利用系数为0.57，节水灌溉中，管灌、喷灌和滴灌的灌溉水利用系数分别是0.8、0.85和0.9。经预测，农业和生态可利用水量Q=14.15 亿m3，每年粮食需求量TDFOOD=35 667.43 万kg。模型中用到的相关数据见表1～表5。

表1 黑河中游生态用水经济效益系数

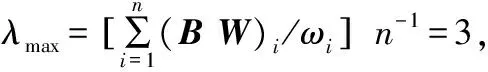
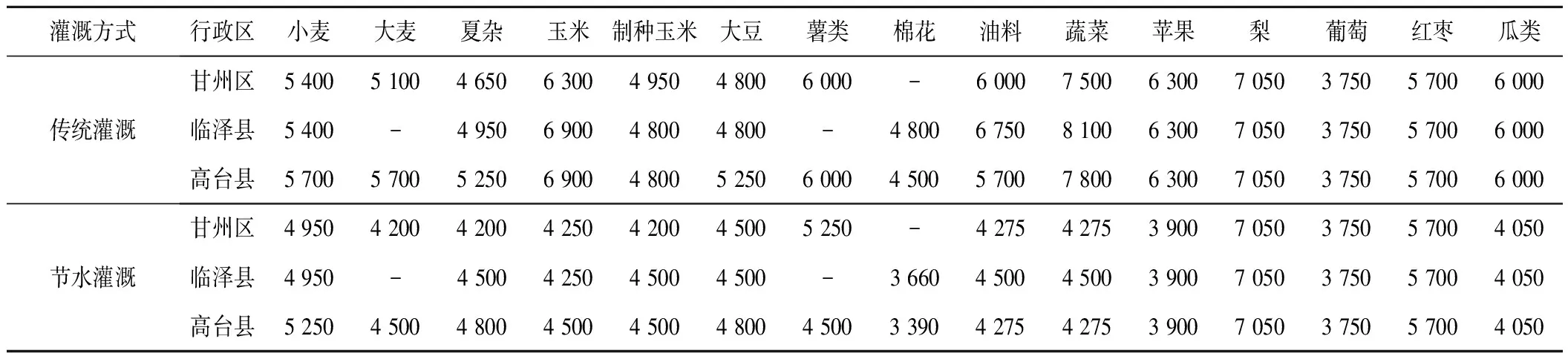
表2 黑河中游农作物灌溉定额 m3/hm2

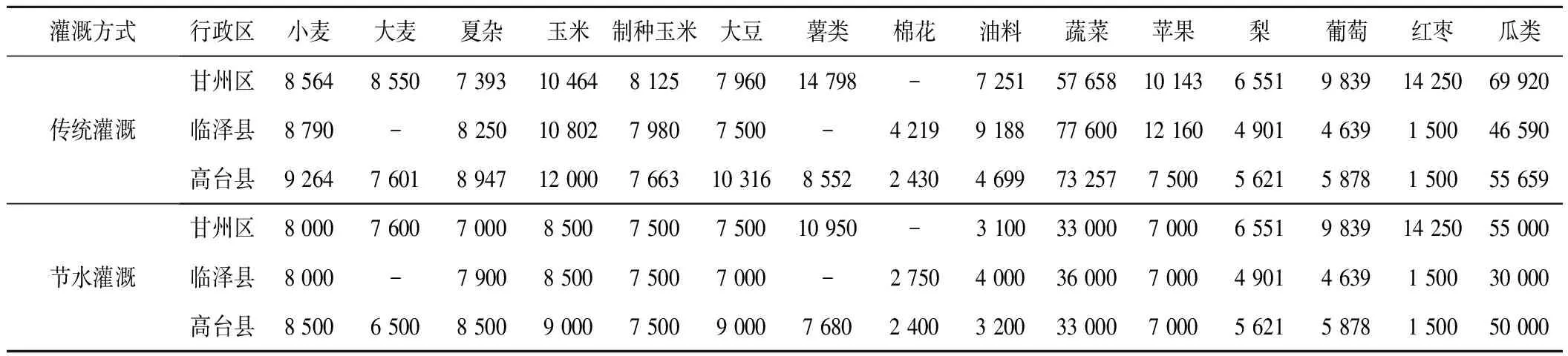
表3 黑河中游农作物单产 kg/hm2

表4 黑河中游农作物价格及成本

注：“①”表示管灌；“②”表示喷灌；“③”表示滴灌。

表5 黑河中游农作物的种植面积 hm2

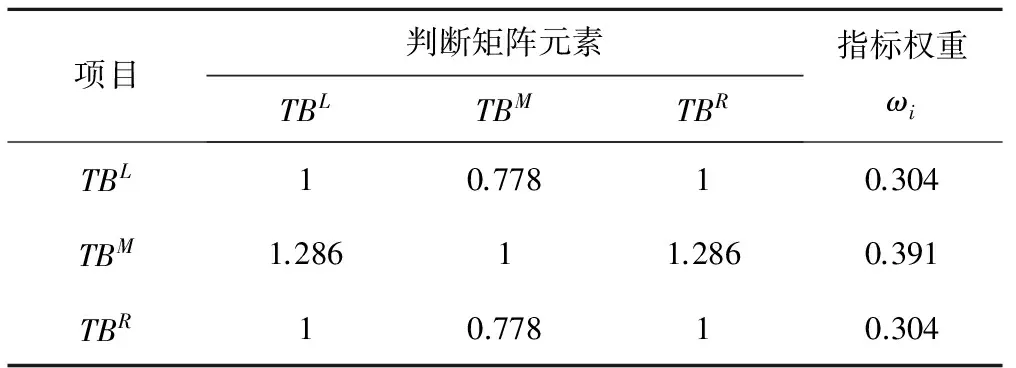
表6 AHP判断矩阵及权重计算结果

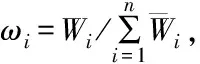
2.2 结果分析

应用上文中的求解算法编程求解，得到黑河中游单目标模糊规划模型优化结果见图2和表7，多目标模糊规划模型优化结果见图3和表8。

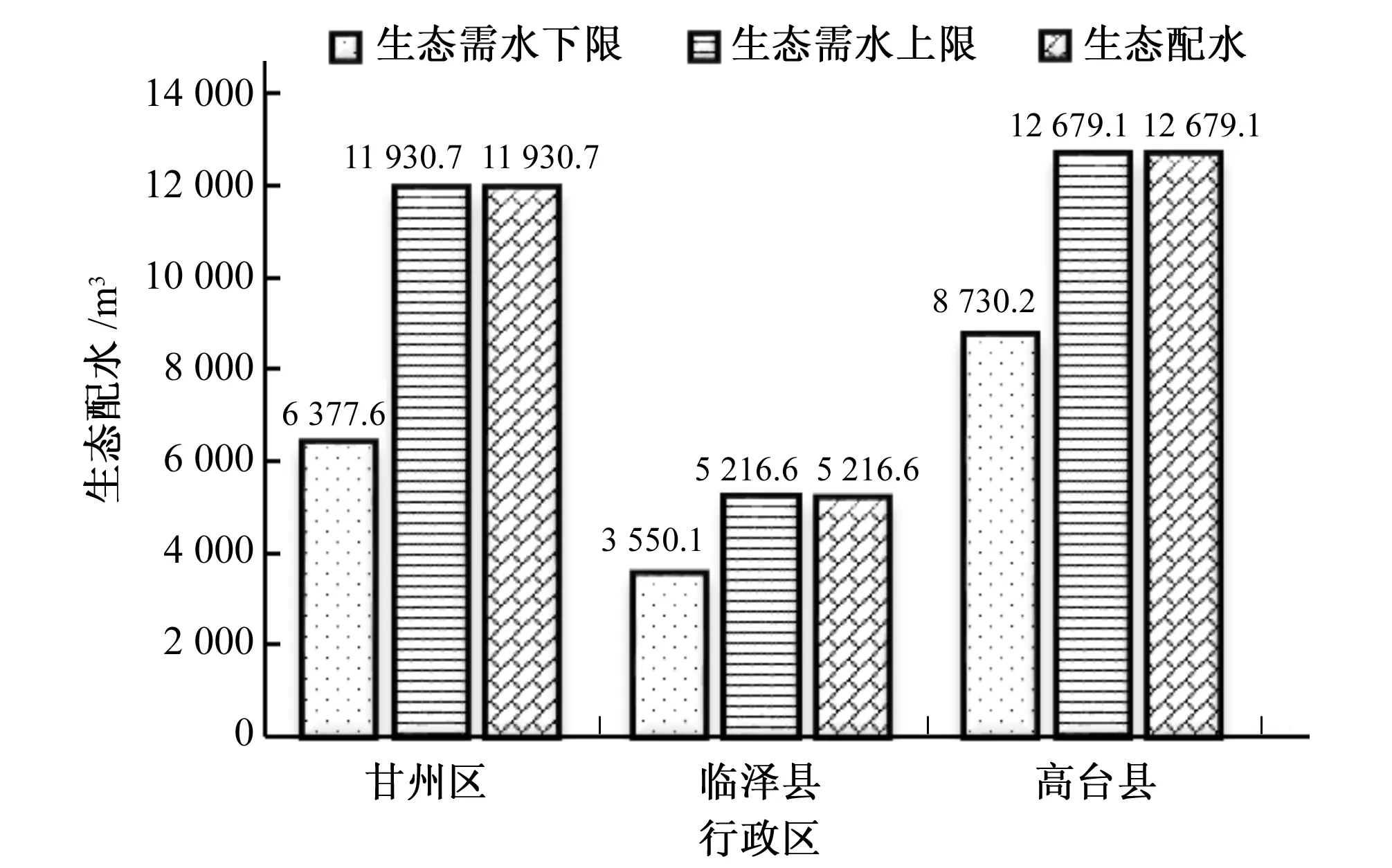
图2 单目标模型生态配水结果

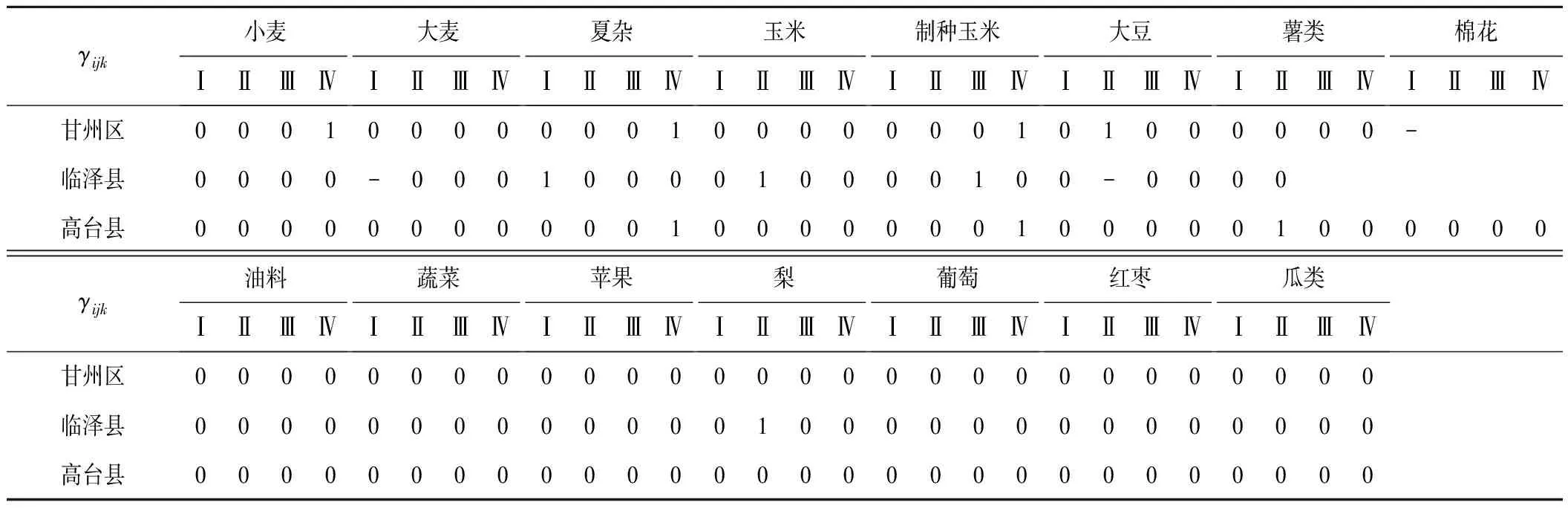
表7 黑河中游单目标模糊规划模型节水灌溉面积优化结果

注：“Ⅰ”、“Ⅱ”、“Ⅲ”、“Ⅳ”分别表示该种作物节水灌溉面积占总种植面积的5%、15%、25%和35%。

分析单目标模型优化结果可以得出：该模型综合考虑了3个因素来选择进行节水灌溉的作物和节水面积，第1个是单方水效益比较低的作物；第2个是实行节水灌溉后单方水效益提高比较大的作物；第3个是该作物总的种植面积。出现这样的结果的原因如下：单目标模型的参数是生态和农业单方水经济效益，而目标函数是经济效益最大，所以单方水经济效益低的作物，即粮食作物就首当其冲成为节水对象，而且，一旦选择了该作物，选择的节水灌溉面积标准就是最大的那个，即35%；其次是对于实行节水灌溉后单方水效益提高比较大的作物，也就是节水效益比较好的作物，它本身效益提高很明显，而且节出来的水还能补给生态效益；最后由于本模型是0-1整数规划模型，节水规模都是事先预设的，这就限制了生态配水的随意性，因此，哪种作物的种植面积搭配上某种节水规模正好能够满足目标函数的要求也会被模型参考。综合上述因素，可以从优化结果中看出，粮食作物如夏杂、制种玉米和大豆等实行了节水灌溉，而经济作物同样因其经济价值高而不宜采取节水灌溉；模型完全地满足了各行政区的生态需水，甘州区、临泽县和高台县的生态配水都达到了生态需水的上限，这说明，生态单方用水产生的经济效益是比较高的，足以让作物做出“牺牲”。

图3 多目标模型生态配水结果

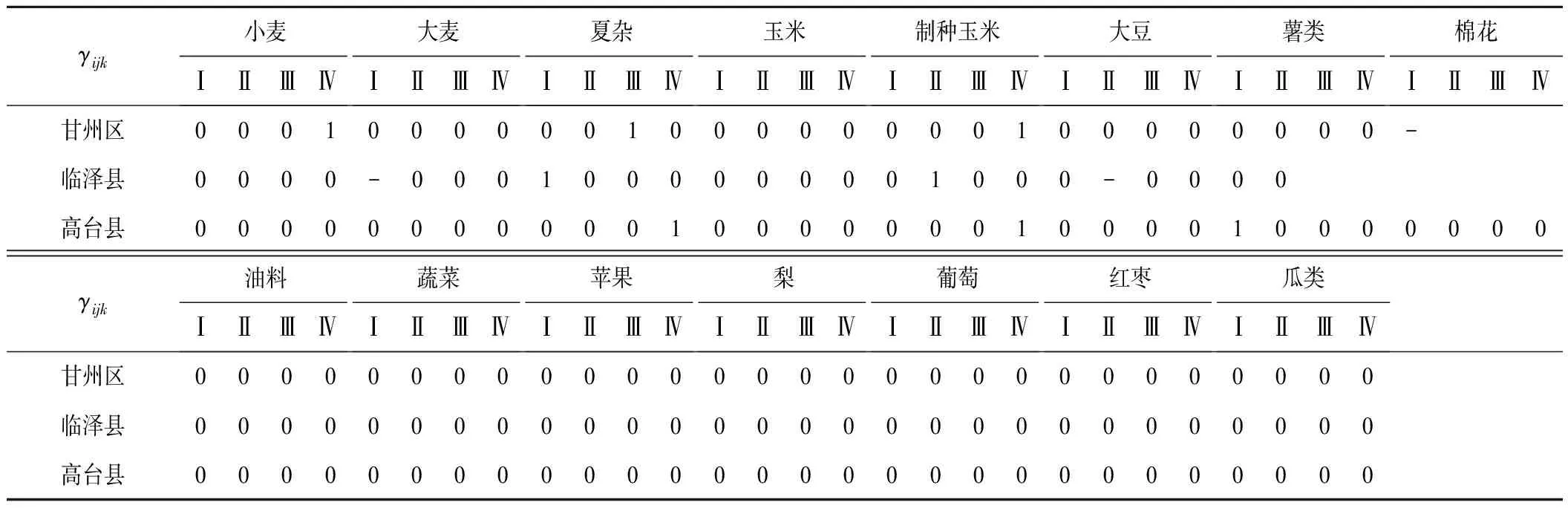
表8 黑河中游多目标模糊规划模型节水灌溉面积优化结果

多目标模型与单目标模型的不同之处在于，单目标模型是同一个经济目标里生态经济效益和作物经济效益在“较量”，而多目标模型是2个不同的目标在权衡。多目标模型跟单目标模型在优化时会遇到相同的问题，那就是哪种作物选择哪种节水灌溉标准。经分析，其选择的准则与单目标模型是一样的，此处不再赘述。综合上述因素，可以从优化结果中看出，粮食作物如小麦和夏杂等实行了节水灌溉，而经济作物因其经济价值高而不宜采取节水灌溉；模型尽可能满足生态目标，因为该模型的生态目标并不具备对各行政区的配水顺序进行限制约束，所以生态配水依次充分满足了甘州区和临泽县，使其生态配水都达到了需水上限，剩下的水都配给了高台县，其生态配水也达到了需水上限的97.8%。

3 结 语

(1)内陆河流域水资源的优化配置可通过节水灌溉措施来保证生态需水，促进生态系统的和谐发展。模型对于干旱内陆河流域，尤其是农业用水比例比较大的区域具有很好的适用性，可以减少农业用水量，并且可以根据研究区域缺水情况设置不同的节水灌溉标准，也具有很好的普及性。

(2)在计算天然植被生态需水时，为了确定各植被类型的实际地下水埋深，本文根据张掖市2004年地下水埋深在ARCGIS下采用IDW空间插值得到的地下水埋深分布图，并用各植被类型能够正常生长的生态水位对其进行修正，使计算结果更符合实际情况。

(3)关于生态价值，不同的学者对其看法不一，考虑到其确实存在模糊性，本文将生态服务价值以模糊数的形式引入模型中，更具有说服力。不过，对生态服务价值的应用是基于他人的研究结果进行的，其存在很大的差异性，今后仍需要更合理的理论来指导生态服务价值的研究。

(4)建立的2个模型可以得到从不同角度出发的各个计算单元的水资源优化配置结果，结果使农业用水比例由原来的84.8%下降到75%左右，有效保证了生态需水，能够为当地的生态保护提供有力的理论依据与决策支持。

[1] 粟晓玲, 康绍忠. 石羊河流域多目标水资源配置模型及其应用[J]. 农业工程学报, 2009,25(11):128-132.

[2] 严登华, 王 浩, 杨舒媛, 等. 面向生态的水资源合理配置与湿地优先保护[J]. 水利学报, 2008,39(10):1 241-1 247.

[3] 石建勋. 考虑灌区生态需水的水资源优化配置研究[D]. 银川：宁夏大学, 2008.

[4] Li Mo, Guo Ping, Zhang Liudong, et al. Multi-dimensional critical regulation control modes and water optimal allocation for irrigation system in the middle reaches of Heihe River basin, China[J]. Ecological Engineering, 2014,76:166-177.

[5] 粟晓玲, 康绍忠, 石培泽. 干旱区面向生态的水资源合理配置模型与应用[J]. 水利学报, 2008,39(9):1 111-1 117.

[6] Costanza Robert, D'Arge Ralph, de Groot Rudolf, et al. The value of the world's ecosystem services and natural capital[J]. 1997,387(6 630):253-260.

[7] Guo Ping, Chen Xiaohong, Li Mo, et al. Fuzzy chance-constrained linear fractional programming approach for optimal water allocation[J]. Stochastic Environmental Research and Risk Assessment,2013,28(6):1 601-1 612.

[8] Zeng Xieting, Kang Shaozhong, Li Fusheng, et al. Fuzzy multi-objective linear programming applying to crop area planning[J]. Agricultural water management, 2010,98(1):134-142.

[9] Yang Xianxian, Guo Ping, Li Mo. Fraction-programming-based crop area planning under engineering water-saving[C]∥ 2014管理工程国际会议. 中国上海, 2014.

[10] 粟晓玲, 康绍忠, 佟 玲. 内陆河流域生态系统服务价值的动态估算方法与应用----以甘肃河西走廊石羊河流域为例[J]. 生态学报, 2006,26(6):2 011-2 019.

[11] 谢高地, 甄 霖, 鲁春霞, 等. 一个基于专家知识的生态系统服务价值化方法[J]. 自然资源学报, 2008,23(5):911-919.

[12] Tianhong Li, Wenkai Li, Zhenghan Qian. Variations in ecosystem service value in response to land use changes in Shenzhen[J]. Ecological Economics, 2010,69(7):1 427-1 435.

[13] 张 超. 浅析生态系统服务价值评价方法[J]. 现代商业, 2013,(3):280.

[14] 孙慧兰, 李卫红, 陈亚鹏, 等. 新疆伊犁河流域生态服务价值对土地利用变化的响应[J]. 生态学报,2010,30(4):887-894.

[15] 粟晓玲. 石羊河流域面向生态的水资源合理配置理论与模型研究[D]. 陕西杨凌：西北农林科技大学, 2007.

[16] 张晨光, 吴泽宁. 层次分析法(AHP)比例标度的分析与改进[J]. 郑州工业大学学报, 2000,21(2):85-87.