基于多目标模糊优化模型的兰州市水资源优化配置研究
2016-03-23乔延丽禄芳霞
张 芮,乔延丽,禄芳霞,毛 兰
(甘肃农业大学工学院,兰州 730070)
20世纪40年代,Masse[1]首次提出了以水资源合理配置为目的的水库优化调度问题,而水资源优化配置的思想真正产生并来源于60年代初期科罗拉多的几所大学对计划需水量的估算及满足未来需水量的途径进行的研讨。随后Pearson[2]等(1982年),英国学者P W~ erbertson[3]等,荷兰学者E Romijn M Taminga[4],先后在考虑不同目标诸如多部门利益的相互矛盾水的多功能性和多种利益前提下开展了以水量配置为主的水资源优化配置研究。从80年代以来区域水资源优化配置研究逐步引起了我国相关学者的重视,贺北方(1988年、1989年)采用大系统分解协调技术求解建立了区域可供水资源大系统优化模型[5,6],翁文斌等(1995年)建立了基于宏观经济的水资源优化配置理论[3],吴险峰等(1997年)从社会、经济、生态综合效益考虑建立水资源优化配置模型[7],吴泽宁等(2004年)提出了区域水资源配置的多目标宏观决策分析方法[8],通过不断的研究促进水资源优化配置方法逐渐趋于成熟。
由于区域水资源系统结构复杂,影响因素众多,各部门的用水矛盾突出,研究成果多以多目标和大系统优化技术为主要研究手段,在可供水量和需水量确定的条件下,建立区域有限的水资源量在各分区和用水部门间的优化配置模型,求解模型得到水量优化配置方案。兰州市受国务院黄河“87”分水方案限制,近几年来所面临的缺水问题越来越严峻,尤其是重经济、轻生态的发展模式更加造成了严重的水体污染,从而加重了区域水质性缺水状况。针对上述问题,本文在综合考虑各个用水部门净效益系数、水利用系数和供水成本的基础上,进行兰州市水资源的优化配置,旨在为实现兰州区域经济发展可持续发展与水环境保护协调发展提供理论依据。
1 研究区概况介绍
兰州市位于甘肃中部地区,是中国版图的几何中心,全市总占地面积1.337 1万km2,属于温带大陆性气候,年平均气温11.2℃,年均降雨量322.1 mm,处于非季风区。兰州市多年来各用水部门用水资料见表1,由此可以看出在2005-2013年之间,兰州市水资源分配量中工业用水最多所占总用水量的比例超过了50%,生态用水最少所占总用水量的比例不足5%,农业和生活用水量居中分别占总用水量的30%和15%左右。
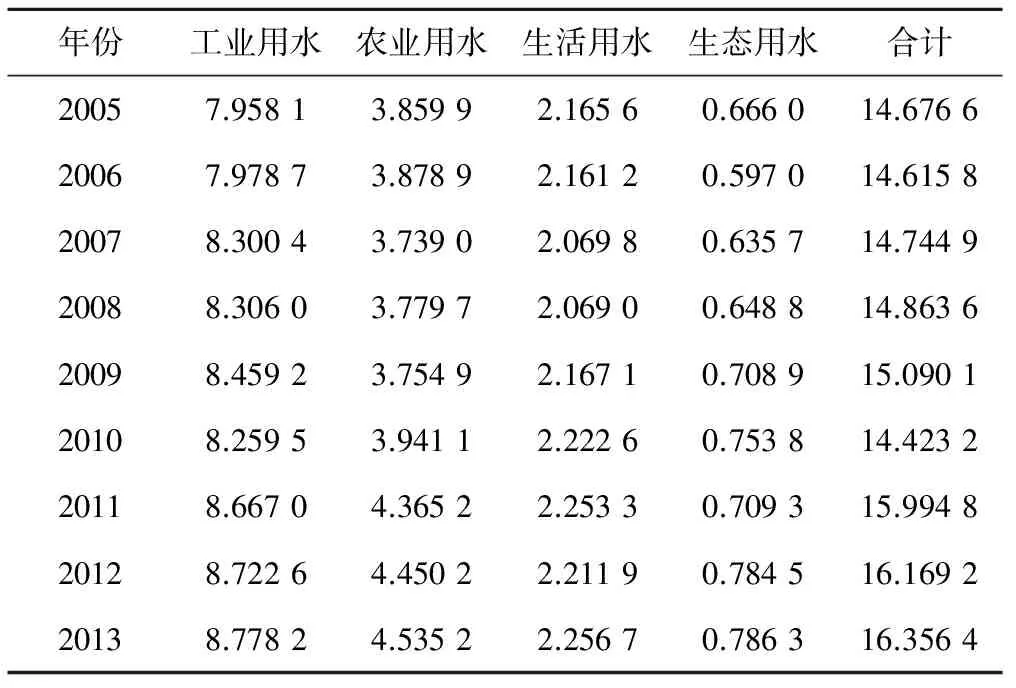
表1 2005-2013年兰州市历史用水量表 亿m3
2 研究方法
2.1 净效益系数确定[9,10]
净效益系数的计算需综合考虑到水资源的经济、社会、生态环境三方面效益,由此确定各用水部门的净效益系数。
(1)工业用水净效益系数。工业用水净效益系数是指供给工业部门单位体积的水所获得的用水净效益(元/m3)工业用水净效益采用产值分摊法计算,计算公式为:
B1=β(Q1/W)/Q1=β/W
(1)
式中:B1为单位工业用水效益,万元/m3;β为工业供水效益分摊系数;Q1为工业用水量,m3;W为工业万元产值耗水量,m3/万元。
(2)农业用水、生活用水、生态用水净效益系数。以单位工业用水净效益系数为基准,则各用水部门的单位用水效益为:
Bi=γiB1i=2,3,4
(2)
式中:γi为其他用水部门用水效益相对工业用水效益的系数。
(3)
式中:Bi为各用水部门单位用水效益,万元/m3;αi、βi、λi为折算系数,i=2,3,4,不同用水部门取不同的值;Qi为个用水部门用水量,m3;Qimin为各用水部门最小用水量,m3;Qimax为各用水部门最大用水量,m3。
2.2 层次分析法和熵值法求解指标融合权重
(1)层次分析法[11]。建立关于各用水部门综合效益最大的指标体系层次关系后,假设现有L个专业权威专家应用“1-9”标度法[9],对体系中m个指标的重要性进行两两比较,生成L个m×n判断矩阵,然后采用特征向量法求出判断矩阵最大特征值对应的特征向量并将其归一化,即为各个专家对层次体系中各指标相对于综合效益做出的主观权重ω′,最后对权重进行一致性检验。
(2)墒值法[12]确定的专家自身权重。熵是简单巨系统的一个重要概念,根据信息熵原理,可以获得各指标中的信息质量,是决策可靠性大小的决定因素之一,信息熵能够很好地反应在评判过程中,指标对结果影响的大小。据此可用信息熵建立专家自身权重来修正由层次分析法获得的主观权重。
根据L个专家对m个指标的评分结果建立m×L阶矩阵,根据各个专家的评分结果一致性的差异大小来度量各专家评分的优劣,即与其他专家评价结果一致性高说明该专家评价结果较优所占权重值大,与其他专家评分结果一致性低则说明该专家评价结果较劣,所占权重值小。各专家的评价水平向量:
Ei=(ei1,ei2,…,eiL)
(5)
i=1,2,…,m,k=1,2,…,j
式中:eik反映了专家Li对目标B(B1,B2,…,Bm)所做的评价结论的水平。
由此建立基于信息墒的专家指标评价模型:
(7)
i=1,2,…,m;j=1,2,…,n
墒值Hi代表不确定程度。墒值Hi越小,专家的决定水平越高,给出的评分可靠性就越高,越科学;反之,熵值越大的专家给出的评价结论可靠性越低,越不科学。因此可采用下式表示第i个专家的自身权重,Ci值越大,表示专家i的意见应在评价中占的比重越大。
(8)

W=w′Ci
(9)
2.3 模糊多目标综合效益系数确定[14]
设区域有n个用水部门表示为:xi={x1,x2,…,xn},样本j的特征值用m个指标特征值表示为xj=[x1j,x2j,…,xmj]T,由此各用水部门的指标特征值用m×n阶矩阵表示为:x={xij},i=1,2,…,m;j=1,2,…,n。
由于各指标的实际值的量纲不同,需对其用公式(6)~(8)进行标准化处理:
越大越优型:rij=xij/maxxj
(10)
越小越优型:rij=minxj/xij
(11)
式中:xij为样本j指标i的特征值;maxxj、minxj分别为n个方案中指标j的最大、最小特征值。
用水部门的各指标分为越大越优和越小越优型两类,通过公式(4)~(7)标准化后获得指标相对隶属度矩阵为:
(12)
应用相对优属度计算公式获得各个用水部门综合效益系数,即:
(13)
2.4 水资源优化配置模型
以区域水资源综合效益最大为目标,建立水资源优化配置的目标函数,以供需水量为约束条件,采用线性规划法[15]求解模型。
(1)目标函数。
(14)
(2)约束条件。
供水约束:
总
(15)
式中:Q总为总的供水量,m3,规划年取不同频率时Q总取不同值。
需水约束:
Qimin (16) 式中:Qimin、Qimax分别为农业、工业、生活、生态需水量的最小和大供水量,m3。 非负约束: Qi≥0i=1,2,3,4 (17) 将兰州市水资源的用水部门分工业、农业、生活、生态4个用水部门。综合考虑区域水资源的净效益系数、水利用系数和供水成本作为综合效益系数的计算指标。 根据水利研究会的相关决定,取β=11%,W=75.25 m3/万元,折算系数αi、βi、λi(i=1,2,3,4)按照文献[6]中的计算方法计算并代入公式(3)计算获得用水各部的折算系数r2=0.875,r3=1.700,r4=1.200;则由公式(1)和(2)计算各用水部门净效益系数见表4。 由层次分析法建立判断矩阵,由最大特征向量法获得各专家给出的主观权重见表2。 表2 各评价指标的主观权重值及一致性检验Tab.2 Subjective weight value and consistency test for each evaluate index 熵值法对各专家给出的主观权重进行修正,根据公式(4)~(8)获得各专家自身权重见表3。 表3 墒值法专家自身评价权重结果Tab.3 The result of experts themselves evaluation weight value 根据公式(9)计算可得指标融合权重为W=[0.478 9,0.200 5,0.165 6]T,归一化结果为W=[0.566 7,0.237 3,0.196 0]T。 确定综合效益系数时需综合考虑各用水部门的净效益系数、水利用系数及供水成本具体特征值见表4。 表4 各用水部门指标特征值Tab.4 The index eigenvalue for each water department 将表4中的数据根据公式(10)和(11)标准处理后各指标特征值的相对隶属度矩阵: (18) 将上式得到指标权重,代入公式(13)当p=2时计算得到非归一化综合效益系数为:uj=[0.595 3,0.659 7,0.925 0,0.940 7],归一化后的综合效益系数为:uj=[0.190 8,0.211 4,0.296 4,0.301 4]。 根据表1中兰州市各用水部门2005-2012年用水历史资料,采用灰色预测法[16,17]预测规划年2020年多年平均需水量预测结果见表5。 表5 规划年2020年各用水部门预测用水量及用水量上、下限 亿m3 注:生态需水和农业需水量的最大最小值可取预测值的20%~30%[6];根据生活用水特性, 其上下限取为等值[18]。 将计算获得的各用水部门综合效益系数代入公式(14)得到水资源优化配置的综合效益最大目标函数: maxE=max{0.190 8Q1+0.211 4Q2+ 0.296 4Q3+0.301 4Q4} (19) 由《甘肃省水中长期规划》获得不同频率下可供水量分别为:P=50%时,Q供=18.34亿m3;P=75%时,Q供=17.35亿m3;P=90%,Q供=16.19亿m3,并将实际数据代入公式(15)~(17)计算得约束条件数学表达式为: 需水约束为: 7.528 0 4.222 5 2.480 0 0.712 5 非负约束:Qi≥0i=1,2,3,4 采用Matlab中线性规划函数Linprog[19]求解水资源优化配置模型得出各用水部门水资源配置结果,见表6。 表6 水资源优化配置结果 Tab.6 The optimized allocation result of water resources 将规划年2020年的水资源预测结果与优化后的结果(频率为多年平均)相比较结果如表7所示。 采用信息熵法修正由层次分析法获得主观权重,获得了更加合理的指标权重。将复杂得多目标寻优问题转化为较简单线性规划问题,使整个模型的求解过程变的较为简单。分配的生态用水量相比较与预测生态用水量增加了0.237 5亿m3,对兰州市的水生态文明建设可持续发展具有积极意义,可为兰州市水资源配置决策提供技术支撑。本文建立了基于综合效益最大的兰州市水资源优化配置模型,其中约束条件不够严谨,有待进一步的完善。 表7 规划年2020年兰州市预测用水量与分配水量增量对照表 亿m3 [1] 贺北方.区域可供水资源优化分配与产业结构调整:大系统逐级优化序列模型[J].郑州工学院学报,1989,(1):56-62. [2] 贺北方. 区域水资源优化分配的大系统优化模型[J].武汉大学学报(工学版),1988,(5):109-118. [3] 李玉河.水资源水质水量优化配置研究进展[J].灌溉排水学报,2008,(3):103-105,120. [4] 吴险峰,王丽萍.枣庄城市复杂多水源供水优化配置模型[J].武汉水利电力大学学报,2000,(1):30-32,62. [5] 吴泽宁,索丽生.水资源优化配置研究进展[J].灌溉排水学报,2004,(2):1-6. [6] 张雪飞,程水源,郭秀锐,等.多目标优化方法在区域水资源优化配置中的应用----以唐山市为例[J]. 安全与环境学报,2006,(4):73-78. [7] 孙文水.水资源优化配置及对城市可持续发展的影响[J].城市道桥与防洪,2012,(4):129-131. [8] 王好芳,董增川.区域水资源可持续开发评价的层次分析法[J].水力发电,2002,(7):12-14. [9] 李天政,贾子超.层次分析法的原理及应用举例[J].内江职业技术学院学报,2008,(4):52-55. [10] 余建星,李彦苍,吴海欣,等.基于熵的海洋平台安全评价专家评定模型[J].海洋工程,2006,(4):90-94. [11] 余建星,蒋旭光,练继建.水资源优化配置方案综合评价的模糊熵模型 [J].水利学报,2009,(6):729-735. [12] 陈守煜,马建琴,张振伟.作物种植结构多目标模糊优化模型与方法[J].大连理工大学学报,2003,43(1):12-15. [13] 康永辉,王宝红.线性规划法在水资源系统规划优化配置中的应用[J].科学之友,2010,(7):6,12. [14] 刘淑慧,程伍群,高 芬,等.GM(1,1)模型预测农业用水量及节水灌溉形式[J]. 节水灌溉,2007,(8):14-16. [15] 杨华龙,刘金霞,郑 斌.灰色预测GM(1,1)模型的改进及应用[J]. 数学的实践与认识,2011,(23):39-46. [16] 张文鸽,黄 强,管新建.区域水资源优化配置模型及应用研究[J]. 西北农林科技大学学报(自然科学版),2005,33(12):153-158. [17] 张德丰. Matlab数值分析与应用[M]. 国防工业出版社,2007,(1):256-260.3 兰州市水资源优化配置
3.1 用水部门净效益系数确定
3.2 指标融合权重的确定
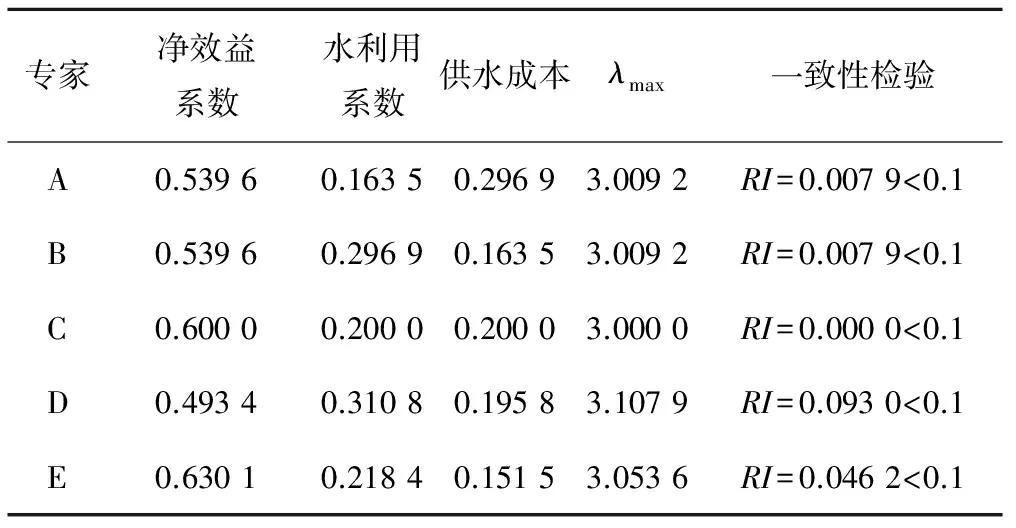

3.3 各用水部门综合效益系数确定
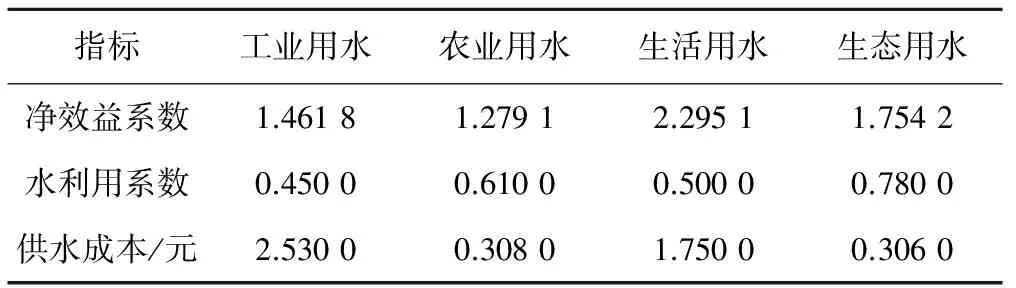

3.4 水资源优化配置
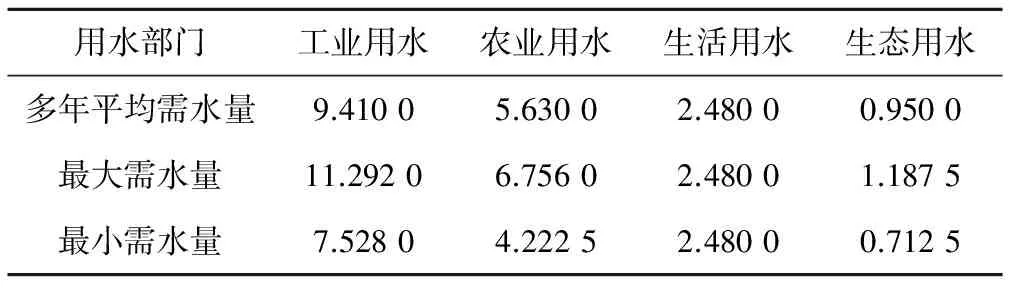


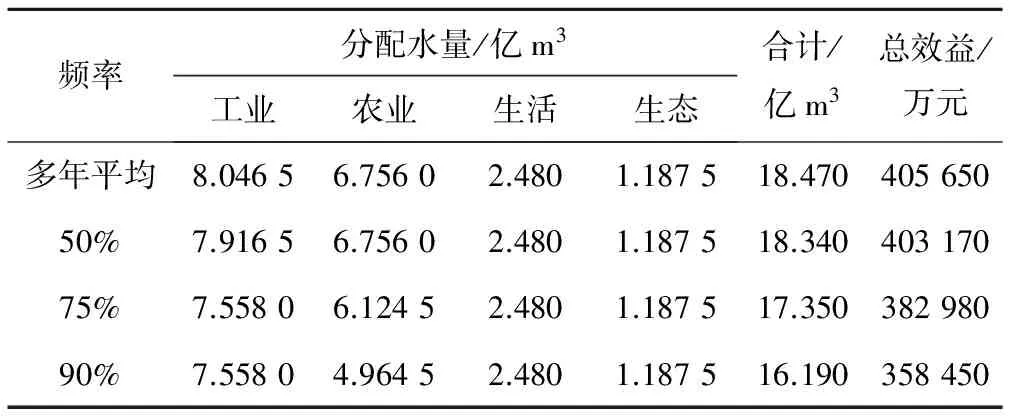
3.5 需水量分析
4 结 语