三支点叉车转向齿轮设计及动力学仿真

裘信国，周鑫卓，周见行，姜　伟，郑　颖，夏中楠，贾中楠

(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014)



三支点叉车转向齿轮设计及动力学仿真

裘信国，周鑫卓，周见行，姜伟，郑颖，夏中楠，贾中楠

(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014)

摘要：为获得三支点叉车转向时，转向齿轮的动力学变化规律，提出基于Hertz理论和虚拟样机仿真的方法.考虑叉车转向的实际情况对助力转向与回正过程中齿轮的转角、角速度、角加速度、圆周力、径向力、轴向力、法向载荷的变化规律进行了仿真研究.结果表明：运用Hertz理论和虚拟样机方法可以有效实现对EPS系统转向齿轮啮合的动力学研究，从而为电动助力转向系统的设计与改进提供理论支持及参考.

关键词：Hertz理论；虚拟样机；电动助力转向；齿轮啮合；动力学仿真

随着物流行业的发展，叉车的发展越来越受到重视，叉车领域的研究越来越多，陈帅人实现了基于捕捉意图的叉车参数化设计系统的研究[1].三支点电动叉车，以三支点为支撑形式，能实现90°转向，具有转弯半径小的特点，广泛应用于空间作业狭小的场所内.三支点电动叉车多配备电动助力转向系统，电动助力转向系统包括电转向系统和机械转向系统两部分，机械转向系统提高了驾驶员的手感，一旦电转向系统失效，机械转向系统依旧可以工作，有效避免了电转向系统失效时影响整车的转向，确保叉车运行安全[2].

电动助力转向系统与机械转向系统和液压助力转向系统相比有着省力、节能、结构紧凑、环保、效率高、随动性强、助力优越、显示角度、自动回正、质量轻、易保养、可移植性高等优点[3].电动助力转向系统已成为国内外高校和企业研究的热点，但目前主要集中在对电转向系统控制器的研究上[4-7]，对与之配套的机械转向很少研究，尤其关于电动助力转向齿轮的研究更少.三支点电动叉车转向时，电机与转向轮之间通过齿轮啮合传递助力，传统设计时，装到车上才发现问题，不仅浪费人力物力，而且很难找到问题所在，提出了基于SolidWorks与Adams联合搭建虚拟样机，对转向齿轮啮合进行动力学仿真，分析了转向与回正过程中，大小齿轮的转角、角速度、角加速度，反应了转向轮的实际运动情况；同时分析了圆周力、径向力、轴向力、法向载荷，并与理论值比较，误差在合理范围内，为三支点电动叉车转向系统的设计提供了理论参考，缩短了开发周期，节省了人力物力，有利于提高转向系统工作的跟随性、稳定性和可靠性.

1转向齿轮设计与虚拟样机搭建

1.1　转向阻力矩

三支点叉车转向时，其主要阻力矩为转向轮与地面的滑动摩擦阻力矩，且系统传动部分的摩擦可用效率η表达；由于原地转向时的阻力最大，为保证所设计转向系统满足工作要求，以此最大阻力矩为计算力矩.以某型叉车为例，其转向轮为实心轮胎，触地情况如图1所示.

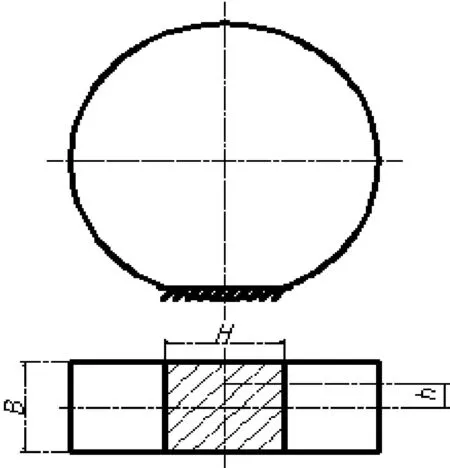
图1　实心轮胎触地情况Fig.1　The situation of solid tire contacting ground

对于实心轮胎，触地图形是边长为H和B的矩形，假定触地部分压力分布均匀，则原地转向时阻力矩计算为

M=Gμh/η=GμB/4η

(1)

式中：M为原地转向时的总阻力矩；G为转向轮所承受最大载荷；μ为滑动阻力系数；h为压力作用点到轮胎触地中心的距离；η为转向系统的传动效率.

1.2　齿轮参数的确定

根据计算转向阻力矩M，选定转向齿轮的传动比i=6.05，选择现有减速比为40的功率为0.25kW，转速为3 000r/min的直流有刷减速电机，可有效克服转向过程中的阻力矩.小齿轮材料为45钢，硬度为280HBS，大齿轮材料为45钢，硬度为240HBS，按齿面接触强度与齿根弯曲强度设计，并结合实际装配空间尺寸，确定转向齿轮参数如表1所示.

表1　齿轮参数

1.3　虚拟样机的搭建

启动迈迪三维设计工具集里的齿轮专家设计系统，按照计算得到的齿轮参数输入设计参数，专家系统会自动生成与之相匹配的尺寸参数，齿轮精度选择7级精度，载荷设置里效率设置为0.97，转速为75 r/min，传递功率设置为226.4 W，可保证大齿轮输出转矩能够克服转向阻力矩，其他参数的设置选择默认，在SolidWorks中生成所需要的齿轮，并在SolidWorks里完成转向机构的装配，导入Adams中，所获得的虚拟样机模型如图2所示.

图2　转向系统三维模型Fig.2　Three-dimensional model of steering system

2齿轮碰撞力的具体分析

齿轮的碰撞力源于轮齿啮入啮出引起的相互作用力，在Adams中将齿轮碰撞力模拟为弹簧阻尼器，并用碰撞函数Impact(x,x,x1,k,e,cmax,d)来计算[8]，Impact函数表达式为

(2)

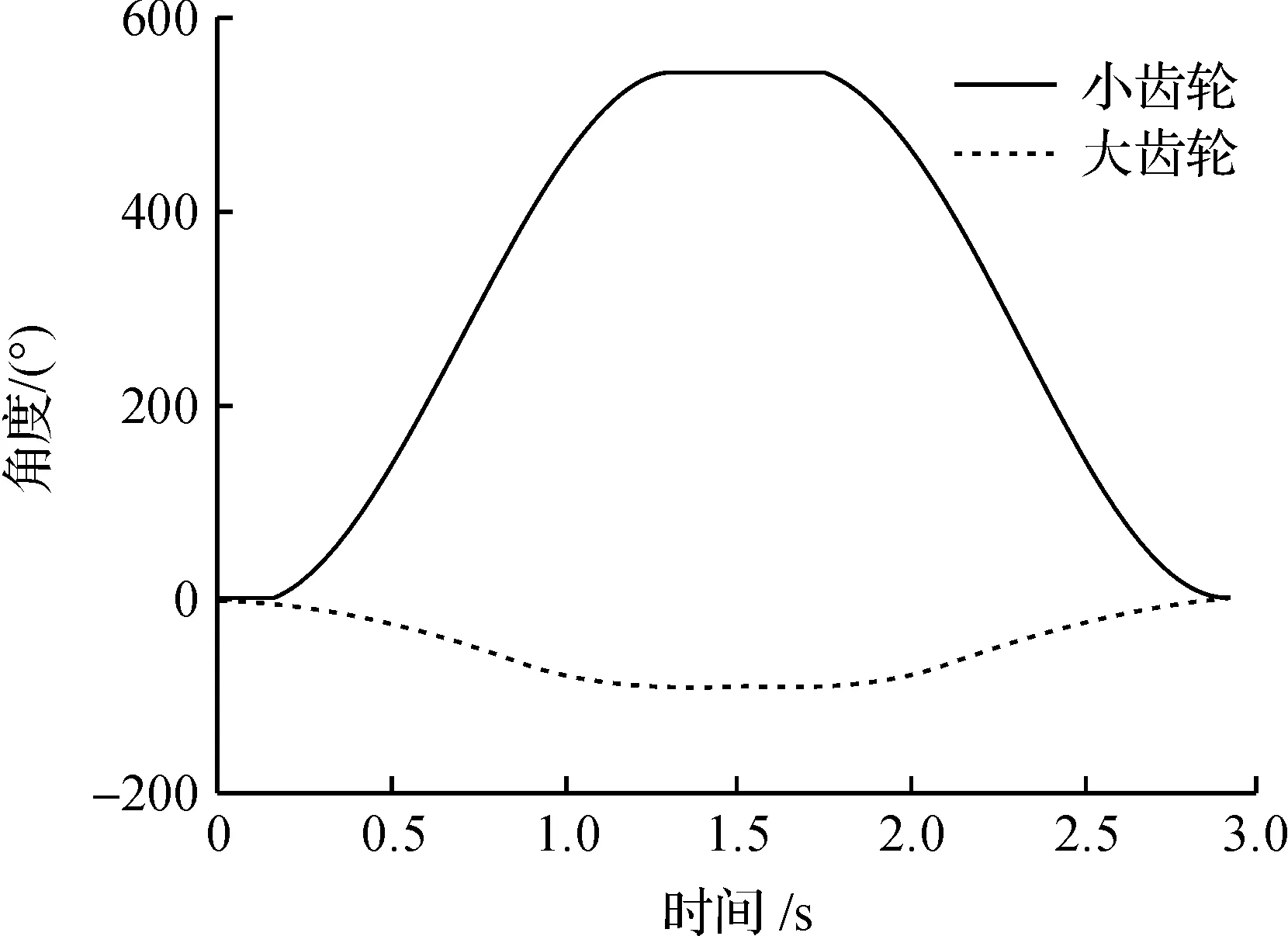
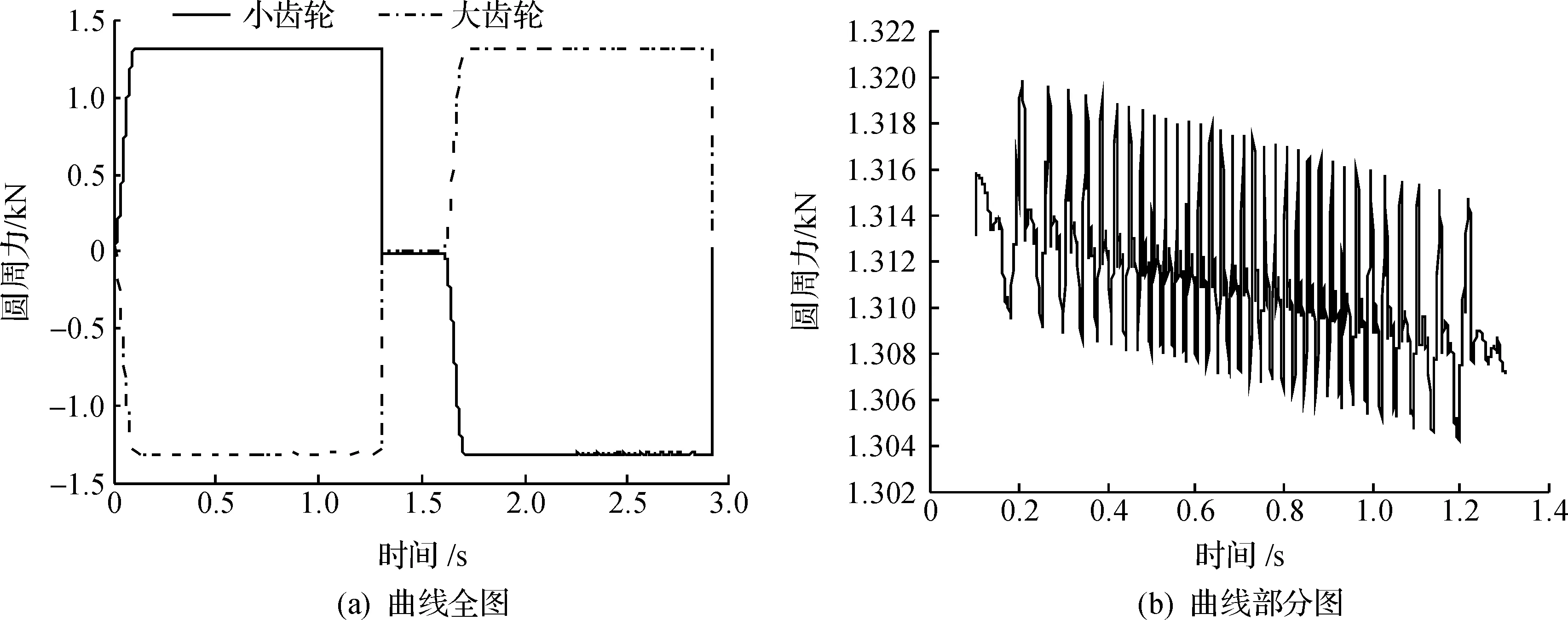
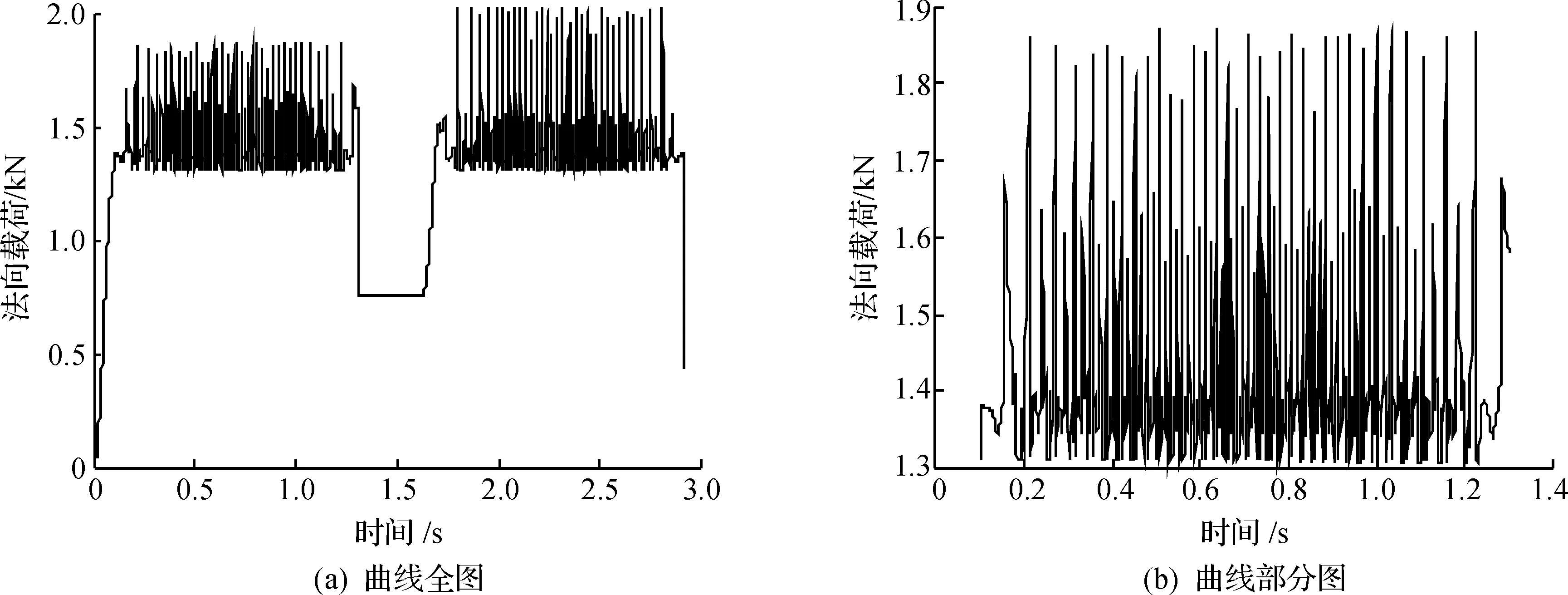
其中：x为两物体间的实际距离；x1为x自由长度的正实数；k为刚度系数；cmax为最大阻尼系数；d为阻尼最大时边界穿透量；e为力碰撞指数，对橡胶材料有[9]，2

可知碰撞力由弹性力与阻尼力两部分组成，弹性力主要受刚度系数k的影响，因此k值的确定非常关键.根据Hertz接触理论[10]，刚度系数计算表达式为

(3)

其中：ρ为综合当量半径；ρ1，ρ2分别为两齿轮在啮合处的各自的当量半径；E1，E2分别为两齿轮各自的弹性模量；μ1，μ2分别为两齿轮各自泊松比.

由于齿轮在啮合过程中啮合点沿着齿轮齿廓推进，两齿轮齿廓曲线上不同点的曲率半径是变化的，综合曲率半径也随之变化的，且两齿轮齿廓曲线上各自的曲率半径均围绕节点处的曲率半径上下变动；齿轮按照标准中心距安装，有啮合角等于分度圆压力角，节圆直径等于分度圆直径，两齿轮齿廓曲线节点处的曲率半径等于各自在啮合点处的当量半径，所以以节点为分析点，有当量半径计算为

(4)

其中：d1为小齿轮分度圆直径；d2为大齿轮分度圆直径；α为分度圆压力角.又因为ρ2/ρ1=d2/d1=μ，联合式(3，4)有

(5)

由式(5)代入数据，可求得k=3.835 1×105N/mm1.5，与碰撞力有关的其他参数设置如下：阻尼系数C=100N·s/mm，穿透深度d=0.1mm，静摩擦系数0.08，动摩擦系数0.05，静阻滑移速度为0.1mm/s，动阻转化速度为10mm/s，碰撞指数e=1.35.

3仿真结果分析

为转向系统各零件添加质量，并添加固定副锁定，为齿轮添加转动副，添加marker点，并创建齿轮副，为小齿轮添加恒定的驱动转速，为了避免由于开始的冲击造成的速度突变及综合考虑电动助力转向过程中，转向轮转过90度，然后回正的运动情况，则转速驱动以阶跃函数施加，在大齿轮上添加负载转矩，由于方向盘施加的力矩比较小，在分析时只添加转向阻力矩即可，并添加齿轮啮合处的碰撞力.为了更直观地分析电动叉车助力转向过程中，转向齿轮啮合的动力学情况，依据实际经验，现设定仿真时间为2.72 s，步长为0.001，可以反映出车轮在整个原地转向过程中齿轮啮合的动力学情况.

叉车转向时，先朝一个方向完成90度的转向，从图3知：齿轮开始时由静止突然加速，角加速度瞬间达到最大，紧接着角加速度呈线性减小到0，与之对应的图4中的角速度曲线变化的斜率逐渐减少到0，且角速度逐渐增大到最大，相应的图5中的转角逐渐增大，且齿轮转角曲线变化的斜率逐渐增大到最大；角加速度过0点后，呈线性增加到最大，与之对应的图4中的角速度曲线变化的斜率逐渐增大到最大，且角速度逐渐减小，相应的图5中的转角逐渐增大，且转角曲线变化的斜率逐渐减小；紧接着角加速度迅速减小到0，与之对应的图4中的角速度及其曲线变化的斜率迅速减小到0，相应图5中的齿轮转角曲线变化的斜率迅速减小到0，转角继续增大到最大值，完成转向，转向轮停止转向.转向结束后，需实现转向轮的回正，电动助力转向系统中，回正由助力完成，其回正过程中各参数的变化和转向过程中恰好相反，由图3，4，5中发现，转向和回正过程中角加速度、角速度、角度的变化满足对称性要求.图6给出了转角随角速度的变化曲线，与上面叙述的变化一致，直观地表示了整个转向过程中角度和角速度之间的关系.

图3　角加速度曲线图Fig.3　Angular acceleration curve diagram

图4　角速度曲线图Fig.4　Angular velocity curve diagram

图5　转角曲线图Fig.5　Rotation angle curve diagram

图6　齿轮角度—角速度Fig.6　Angle-angular velocity of gear

因起步冲击，齿轮啮合圆周力发生突变，变化幅度很大，0.1 s以后啮合力周期性的围绕一个静载均值在比较小的幅度内上下波动，表明齿轮啮合过程中具有一定的动载特性，存在着一定的冲击振动，而且啮合圆周力并非是对称循环的，但啮合圆周力逐渐趋于稳定的周期性的变化，是周期性啮合的良好体现.理论上，在转向过程与回正过程中，大小齿轮所受到的啮合圆周力应该是大小相等，方向相反，且各自呈对称性变化，与仿真结果图7(a)中曲线走向一致.理论上Ft=2T/d1=1 309 N，其中T为小齿轮输出的负载转矩，取圆周力在转向过程中的数据分析见图7(b)，经计算得仿真中的均值为1 311.3 N，则理论与仿真的误差为0.2%，在合理的允许范围内.

图7　圆周力曲线图Fig.7　Circle force curve diagram

理论上，在转向过程与回正过程中，大小齿轮所受到的啮合径向力应该是大小相等，方向相反，与仿真结果图8(a)中曲线走向一致.理论上Fr=Ft·tanα=476.44 N，取径向力在转向过程中的数据分析如图8(b)所示，经计算得仿真中的均值为475.48 N，则理论与仿真的误差为0.2%，在合理的允许范围内.

齿轮啮合法向力，是圆周力和径向力的合力，可由公式Fn=Ft/cosα得到，其中Fn为法向力，Ft为圆周力.在转向过程中，开始时因径向力为0，由图7(a)和图9(a)知：此时法向力与圆周力变化一致；之后由于径向力与圆周力均围绕一个均值波动，可知法向力也应该围绕一个均值波动，与图9(a)中法向载荷的变化一致.理论Fn=Ft/cosα=1 393 N，取法向载荷转向过程中的数据分析如图9(b)所示，经计算得仿真中的均值为1 421.8 N，则理论与仿真的误差为2.1%，在允许范围内.

齿轮啮合轴向力在整个转向和回正过程中，大小齿轮所受到的轴向力在理论上应该大小相等，方向相反，与仿真结果图10(a)中轴向力的曲线走向一致.且理论上轴向力为0，取轴向力在转向过程中的数据分析见图10(b)，可发现其围绕一个接近0的均值上下波动，经计算均值为0.004 2 N，约等于0，误差在正常范围内.

图8　径向力曲线图Fig.8　Radial force curve diagram

图9　法向载荷曲线图Fig.9　Normal load curve diagram

图10　轴向力曲线图Fig.10　Axial force curve diagram

对虚拟样机模型输出仿真数据与理论数据进行了比较，仿真数据和理论数据能够很好的吻合，结果表明了Hertz理论应用到转向齿轮仿真当中是可行的，能够很好地反映转向齿轮的动力学情况，反映了在转向与回正过程中，转向轮的运动情况.

4结论

运用Hertz理论和虚拟样机方法可以有效实现对三支点电动叉车助力转向齿轮啮合的动力学研究，得到了转向与回正过程中，齿轮转角、角速度、角加速度、圆周力、径向力、轴向力、法向载荷的变化规律，为设计与改进三支点电动叉车助力转向系统奠定了基础，具有很好的应用价值.通过对转向齿轮的动力学仿真，理论与仿真结果基本吻合，综合各曲线的走向，所搭建模型符合设计要求，避免了传统设计时，装到车上才发现问题，浪费人力物力，很难找到问题的情况，有效缩短了转向系统的研发周期，降低了成本.

参考文献：

[1]陈帅，姜少飞，洪滔，等.基于设计意图捕捉的叉车参数化设计系统研究[J].浙江工业大学学报，2011,39(6):639-643.

[2]张莉.国内外三支点电动叉车概述[J].叉车技术，2003(2):4-6.

[3]王迅.电动助力转向系统(EPS)技术现状与发展[J].湖北汽车工业学院学报，2008,22(3):21-22.

[4]邱明，杨家军，刘照，等.基于H_∞鲁棒控制原理的电动助力转向系统研究[J].华中科技大学学报，2002,30(12):71-73.

[5]周平，刘峰，方凯.电动叉车电动转向系统控制器的设计[J].工程机械，2004(5):18-21.

[6]施国标，申荣卫，林逸.电动助力转向系统的建模与仿真技术[J].吉林大学学报(工学版)，2007,37(1):31-36.

[7]MAROUF A, DJEMAI M, SENTOUH C, et al. A new control strategy of an electric-po-wer-assisted steering system[J].Vehicular technology,2012,61(8):3574-3589.

[8]石莹，江亲瑜，李宝良.基于虚拟样机技术的渐开线齿轮啮合摩擦动力学研[J].润滑与密封，2011,36(7):32-35.

[9]刘苗.基于虚拟样机技术的齿轮啮合分析[J].装配制造技术，2010(4):12-14.

[10]毕凤荣，崔新涛，刘宁.渐开线齿轮动态啮合力计算机仿真[J].天津大学学报，2005,38(11):991-995.

(责任编辑：刘岩)

Design and dynamic simulation for the steering gear of the three fulcrum forklift truck

QIU Xinguo, ZHOU Xinzhuo, ZHOU Jianxing, JIANG Wei, ZHENG Ying,XIA Zhongnan, JIA Zhongnan

(Key Laboratory of Special Purpose Equipment and Advanced Manufacturing Technology, Ministry of Education,Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:In order to obtain the dynamic changing pattern of three fulcrum forklift steering gear,a method based on the simulation of virtual prototype and Hertz theory was proposed.During the process of the power steering and the power steering reversal ,considering the actual situation of forklift steering,the research on the dynamic changing pattern of the gear angle, angular velocity, angular acceleration, angular acceleration, circumferential force, radial force, axial force, normal load was carried out .The results show that the dynamic research on steering gear meshing of the EPS system can be effectively realized by the Hertz theory and virtual prototyping method, which can provide theoretical support and reference for the design and improvement of electric power steering system.

Keywords:Hertz theory; virtual prototype; EPS; gear meshing; dynamic simulation

中图分类号：TH117.1

文献标志码：A

文章编号：1006-4303(2016)01-0023-05

作者简介：裘信国(1978—)，男，浙江绍兴人，助理研究员，博士，主要从事机械动力学分析研究，E-mail：xgqiu@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(51105338)

收稿日期：2015-09-08