基于Hertz接触理论的齿轮接触分析

胡夏夏，宋斌斌，戴小霞，刘晓曼

(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014)



基于Hertz接触理论的齿轮接触分析

胡夏夏，宋斌斌，戴小霞，刘晓曼

(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014)

摘要：由于齿轮啮合过程中齿廓接触点曲率半径变化以及单双啮合交替的存在，而引起齿面载荷分布不均匀和冲击的问题，根据Hertz接触原理对接触模型和接触应力进行了研究.分析提取啮合线上不同啮合点的综合曲率半径，利用包络线绘制一条连续的曲率曲线，并根据该曲线生成特征曲面；利用有限元方法分别对齿轮接触、特征曲面与平板之间接触进行了接触应力分析；分析结果显示两种接触模型的接触应力分布相似度比较高，简化后的齿轮接触理论模型可为齿轮接触应力实验分析提供参考依据.

关键词：Hertz接触原理；综合曲率半径；有限元；接触应力

渐开线齿轮是工程应用最为广泛的机械零件之一，齿轮传动具有传递功率大、传动比准确、安全可靠等优点.但是齿间接触属于高副，因此接触区域必然会存在应力集中现象，齿轮的接触应力循环作用下容易产生齿面接触疲劳现象.国内外有不少研学者对齿轮啮合过程中接触应力做过大量研究，并取得了丰硕的成果[1-4].但是大多数学者仅研究了节点啮合位置的接触应力，而对接触线上不同位置接触应力分布的研究较少，且相对精确的齿轮接触应力实验模型方面的研究就更少了.因此，开展对接触模型以及接触应力分布的研究有着重大实际意义[5].本研究根据Hertz接触原理[6]对齿轮接触模型和接触应力分布进行了分析，对比了简化前后齿轮接触模型的接触应力分布情况，为齿轮接触应力的实验分析提供了理论参考.

1简化模型的建立

1.1　Hertz接触原理

渐开线齿轮齿面为形状较复杂的特殊曲面，由于接触区宽度小于齿面在接触区域的曲率半径，因而可对啮合齿面作适当简化.Week等[7]试验结果表明：当运转条件相同时，轮齿间的接触状态可用一对滚子来模拟(图1)，一对轮齿之间的啮合可以转换为两个圆柱体沿其母线的接触.图1中两个圆柱体滚子的半径R1,R2分别为齿轮啮合位置的曲率半径.

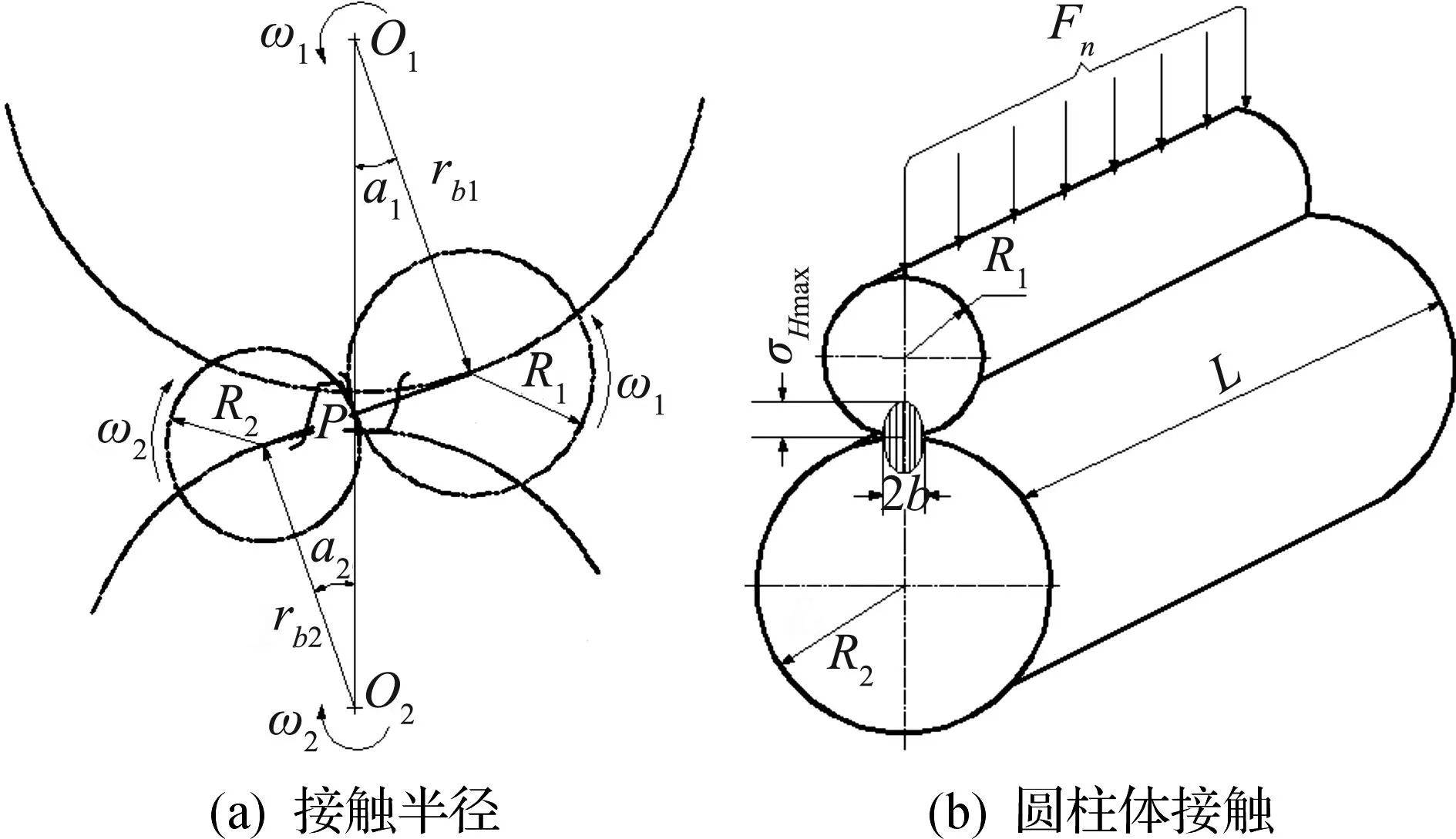
图1　接触模型简化示意图Fig.1　A simplified contact model

由Hertz接触理论推出的接触区最大触应力σH公式[8]为

(1)

(2)

式中：ZE为配对齿轮的材料系数；Fn为载荷；b为两圆柱体的接触宽度；ρ为综合曲率半径；ρ1，ρ2分别为两圆柱体接触线处的曲率半径.

齿面接触应力的计算是以两圆柱体接触时的最大接触应力推到出来的.由渐开线性质可知：一对齿轮啮合过程，由于齿轮表面啮合位置不同，可以看成为两个曲率半径随时变化着的平行圆柱体的接触过程，故各啮合位置的接触应力各不相同[9].因此，图1中一对轮齿的啮合可以简化成一对对应接触半径圆柱体的接触，建立了二个数值分析模型，下文将对其合理性进行验证.

1.2　特征曲面的生成

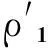
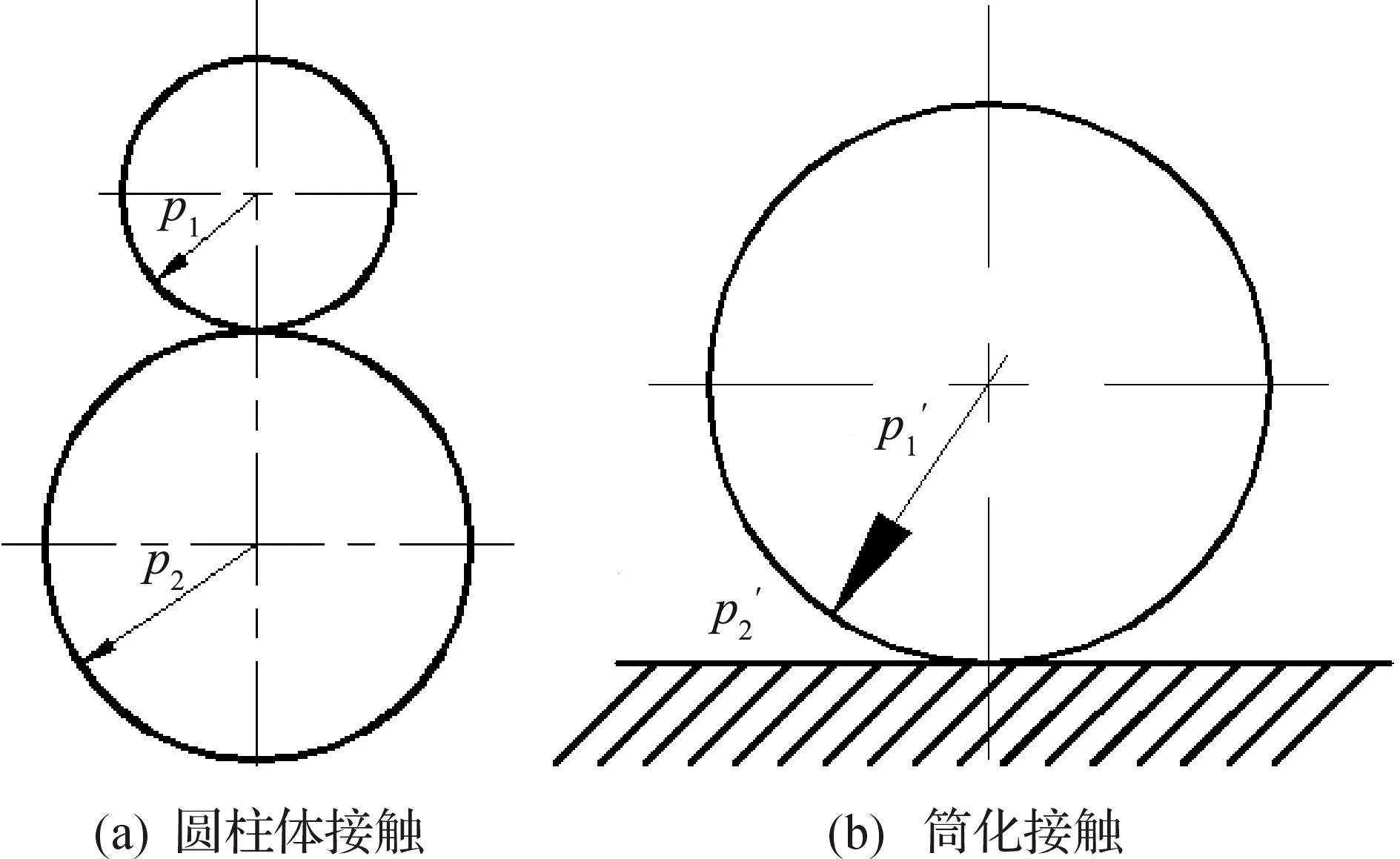
图2　综合曲率半径等效过程Fig.2　Equivalent process of synthetical curvature radius

同理，可将齿轮啮合线上每个啮合点通过图2的方法等效成一个综合曲率半径圆柱体与一个平板之间的接触.由齿轮啮合传动示意图以及齿轮各个参数的关系得出啮合线上两齿面的综合曲率半径为

(3)

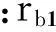
将综合曲率半径数值曲线导入到二维绘图软件AutoCAD中，利用包络线原理绘制出的综合曲率曲线[10]，如图3所示.图3中加粗曲线为综合曲率半径数值曲线，通过450个曲率圆包络成综合曲率曲线.最后在三维软件Pro/E中根据综合曲率曲线生成特征曲面.因此，特征曲面上的曲率半径的变化符合所研究直齿圆柱齿轮中一对轮齿从啮入到啮出过程中综合曲率半径的变化特征.在相同边界条件下，特征曲面与一平板的接触模型和齿轮接触模型在接触应力分布方面应具有一定相似度.

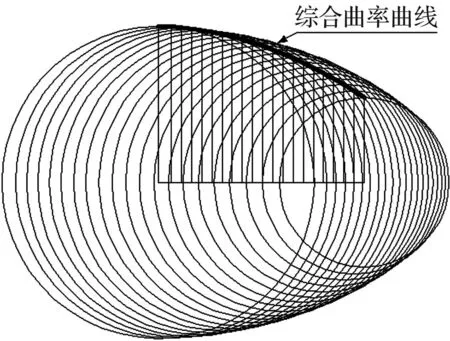
图3　综合曲率曲线形成过程Fig.3　A form process of synthetical curvature curve

2模型接触分析

2.1　载荷的确定

渐开线直齿圆柱齿轮在啮合过程中，为保证传动的连续性和平稳性，重合度ε必须大于1.当重合度ε在1~2之间时，啮合线两端各有一段两对轮齿同时啮合的区段，在这两区段里，每对齿轮副只承受一部分载荷；啮合线中间有一段只有一对轮齿啮合的区段，在这一区段里，由一对轮齿承受所有载荷.然而，载荷在同时啮合的轮齿之间存在一个分配问题，即载荷分配系数XΓ.根据ISO425E中关于XΓ的表达式[11]以及齿轮啮合过程示意图，如图4所示，齿轮啮合线上载荷分配系数的计算式为

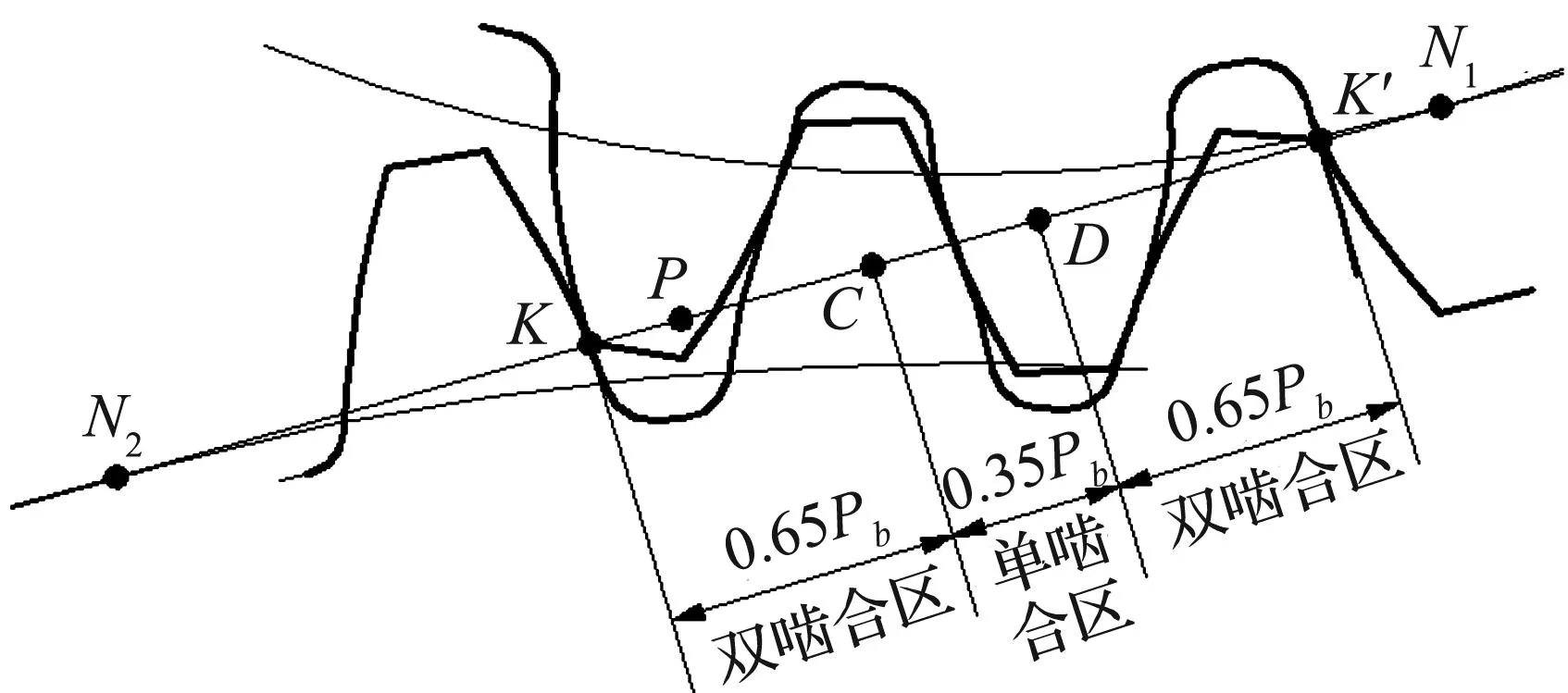
图4　齿轮啮合过程示意图Fig.4　Gear meshing process

(4)

式中：啮合点P从啮入点K向啮出点K′逐渐移动；XΓ为啮合点K点处轮齿的载荷分配系数.运用MATLAB对式(4)求解并得到啮合点位置与载荷分配系数的关系曲线，如图5所示.

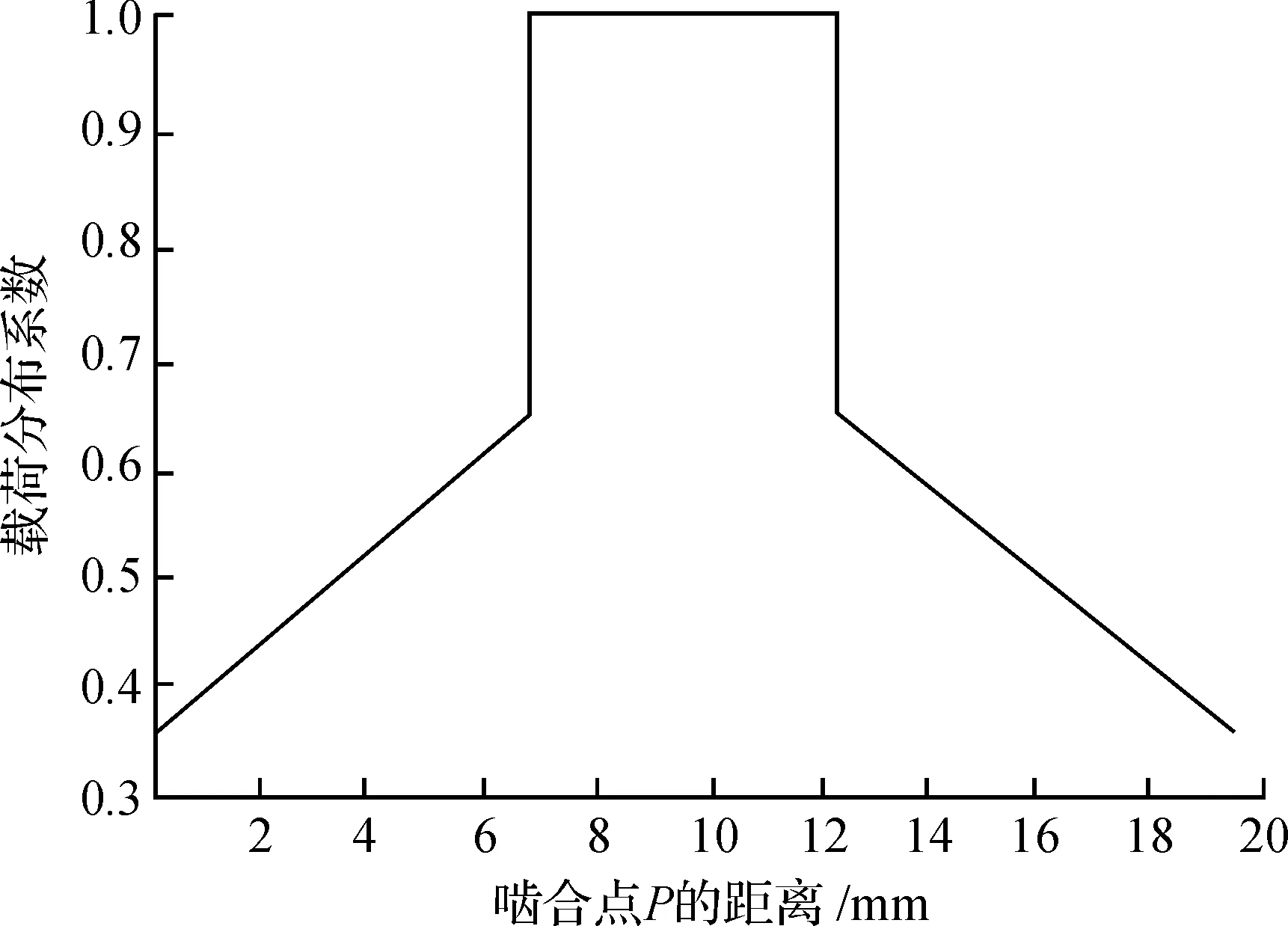
图5　载荷分配系数与啮合位置关系图Fig.5　A load distribution coefficient via meshing position

2.2　接触应力分析及结果

在Pro/E中建立实体模型，通过无缝接口将实体模型导入到ANSYS Workbench中，选择材料属性，划分网格，完成有限元模型的建立.采用ANSYS Workbench接触分析模块，由于齿轮接触时表面既有滚动又有滑动，因此接触类型设置为Frictional，摩擦系数为0.06[12]，计算时的接触算法控制方程设置为Augmented lagrange.增广拉格朗日法比罚函数法加大了接触力的计算，对接触刚度变得不敏感，减少了接触渗透量，但会导致非线性计算迭代次数增多，因此大变形Large deflection要设置为ON.设置弹性模量E=211 GPa，泊松比μ=0.277，接触刚度系数K=1.

从动轮内圈约束条件设置为固定约束Fixed support，主动轮约束条件为Cylindrical support并且保留Tangential方向上的自由度[13].在主动轮上施加T=165 000 N·mm的动力扭矩，则单齿啮合区段齿间法向载荷Fn=2T/d2=1 833.3 N.在两个双齿啮合区段上各取5个啮合点，在单啮合区段上取4个啮合点，利用ANSYS Workbench计算，并利用后处理查看齿面接触应力的变化云图，如图6所示.

图6　ρ=6.650啮合点接触应力Fig.6　Contact stresses of ρ=6.650

本次接触分析一共提取了啮合线上均匀分布的14个接触点作为研究对象，近似得到单个轮齿在一个啮合周期内的接触应力变化规律，结果如表1所示.啮合线上均匀分布的14个接触点作为研究对象，近似得到单个轮齿在一个啮合周期内的接触应力变化规律，结果如表1所示.

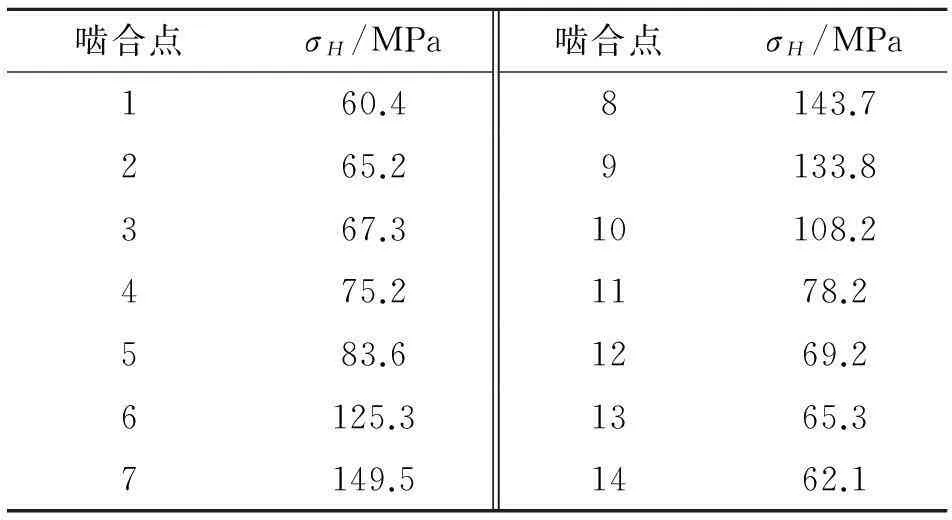
表1　齿轮各啮合点接触应力值

根据载荷分配系数XΓ分别求得14个啮合点处的法向载荷Fni(i=1,2，…,14)，如表2所示.

利用接触分析模块求解出特征曲面与平板对应接触点的接触应力，如图7所示.本次接触分析同样提取特征曲面上均匀分布的14个接触点，得到特征曲面上接触应力变化情况，如表3所示.

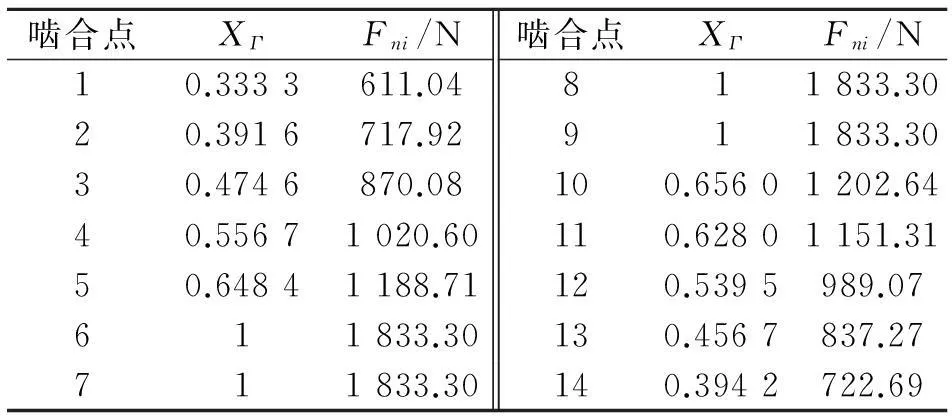
表2　啮合点法向载荷

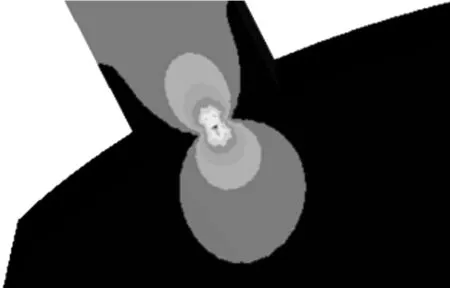
图7　特征曲面上ρ=6.650位置接触应力Fig.7　Characteristic surface stresses(ρ=6.650)

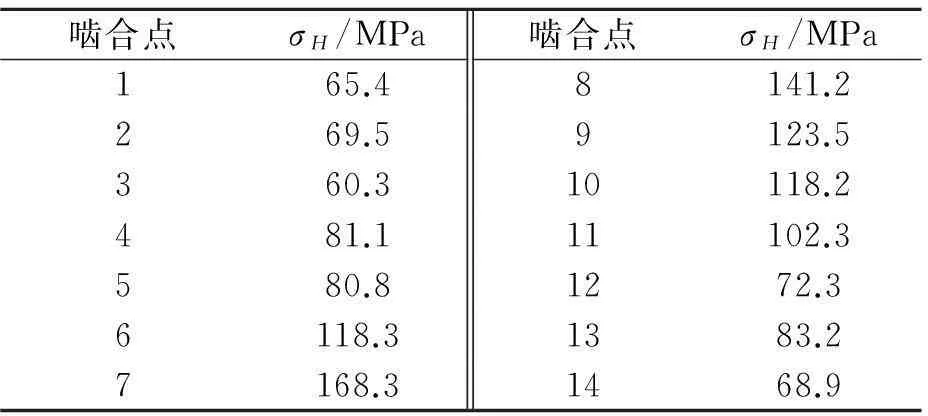
啮合点σH/MPa啮合点σH/MPa165.48141.2269.59123.5360.310118.2481.111102.3580.81272.36118.31383.27168.31468.9

2.3　结果对比

根据表1和表3所得数据，得到两种模型的接触应力变化趋势，如图8所示.随着齿轮开始进入双齿啮合区，载荷分布系数慢慢增大，两种模型1~5号接触点的接触应力都呈逐渐上升趋势；进入单齿啮合区段，两种模型的6~9号接触位置都出现了应力峰值；之后由于再次进入双啮合区段，10~14号接触点应力逐渐下降.

两种模型接触应力计算结果表明:在接触过程中经简化后的接触应力模型与齿轮接触模型在接触应力分布趋势上相似度比较高，说明笔者提出的简化模型在模拟齿轮啮合过程中接触应力方面具有一定的准确性和可行性.

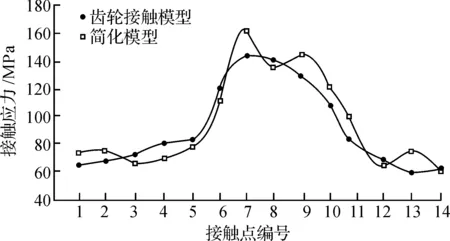
图8　接触应力Fig.8　A distribution of contact stresses

3结论

根据Hertz接触原理以及综合曲率半径的等效法将曲面之间的接触等效成曲面与平面之间的接触，并利用载荷分配系数提取了不同接触位置的动力载荷，利用有限元分别对两种模型进行接触应力分析.分布曲线表明：两种模型在接触应力分布趋势上相似度比较高，因此简化模型的方法具有一定的合理性.由于齿轮的啮合是一个连续的运动过程，可将简化模型(特征曲面与平板的接触)转变成特征曲面凸轮与平板接触的实验模型.通过主动件凸轮的旋转而达到不同综合曲率半径之间的接触，可以模拟齿轮接触过程的接触应力变化，本研究可为齿轮接触应力实验分析提供一定的理论依据.

参考文献：

[1]李碧波，李素有，吴立言，等．渐开线齿轮接触应力分布规律的研究[J]．机械与电子，2010(6):69-71.

[2]LI Shuting. Gear contact model and loaded tooth contact analysis of a three-dimensional, thin-rimmed gear[J].Journal of mechanical design, 2002,124(3):511-517．

[3]张永栋，谢小鹏，廖钱生，等．基于有限元方法的齿轮接触仿真分析[J]．滑与密封，2009，34(1)：49-51．

[4]李杰，孙青军，王乐勤．渐开线齿轮的接触分析[J].工程设计学报，2009，16(1)：27-31．

[5]杨凡，孙首群，于建华，等．齿轮啮合过程中接触力的精确分析[J]．机械传动，2010，34(7)：56-59．

[6]WECK M, KRUSE A, GOHRITZ A. Determination of surface fatigue of gears material by roller test[J]. Journal of mechanical design,1978(100):433-439．

[7]唐锐，张敬东，张祺．新型齿轮传动副建模及接触分析[J]．机械传动，2013，37(2)：76-79．

[8]冯剑军，谭援强．基于Hertz理论圆柱和平面之间的滑动接触分析[J]．摩擦学学报，2009(4):346-350.

[9]包家汉，张玉华，薛家国，等．齿轮啮合过程齿间载荷分配的有限元分析[J].机械传动，2004，28(5)：14-17．

[10]金寿松,徐泽侠,杨东坡，等.基于VB和AutoCAD的齿轮滚刀鉴定系统研究[J].浙江工业大学学报,2013,41(5):514-518.

[11]李庆远．渐开线圆柱齿轮的载荷分配系数与齿间载荷分布系数[J]．昆明理工大学学报(理工版)，1986(4)：22-26.

[12]高创宽，李群.齿面粗糙纹理方向对轮润滑的影响[J].工程设计报，2014(4)，393-397．

[13]金玉萍.QTZ63塔式起重机有限元分析[J].浙江工业大学学报，2010，38(3):242-245.

(责任编辑：刘岩)

Research of gear contact based on Hertz contact theory

HU Xiaxia, SONG Binbin, DAI Xiaoxia, LIU Xiaoman

(Key Laboratory of Special Purpose Equipment and Advanced Manufacturing Technology, Ministry of Education, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:The problems of uneven load distribution and impact are caused by a curvature radius variation and a single-double meshing area in the process of gear meshing. Contact models and contact stresses are studied based on the Hertz contact theory. Synthetical curvature radii in different meshing positions are obtained after analysis, and by using an envelope line a continuous curve is drawn, and a characteristic surface based on the curve is generated. A gear contact model and a curved surface-plane contact model are analyzed through Finite Element method. The results indicate that the stress distributions of the two contact models are similar, the simplified gear contact model may provide a reference basis for gear contact stress experiment analysis.

Keywords:Hertz contact theory; synthetical curvature radius; finite element method; contact stress

中图分类号：TH132.413

文献标志码：A

文章编号：1006-4303(2016)01-0019-04

作者简介：胡夏夏(1963—)，男，浙江湖州人，教授，主要从事机械结构和动力学方面的研究，E-mail：xxhu@zjut.edu.cn.

收稿日期：2015-09-14