比重瓶法处理水样瓶加澄清水重计算方法

吴彰松，张根广，梁宗祥，史志鹏(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

0 引 言

水体中的含沙量测验，是河流水文观测、河工模型试验、水质评价及工农业取水中必不可少的测验要素，对于上述课题研究领域具有举足轻重的作用。在实际含沙量测验中，通常采用比重瓶法[1]。比重瓶法也称为置换法，它是采用预先率定好的比重瓶灌装浑水水样，进行称重及水温测验，之后用浑水重减去同温度清水重，两者差值除以比重瓶体积，再乘以水沙置换系数即得到水体含沙量[2]。

在实验室，采用比重法进行含沙量测验时，通常用蒸馏水或去离子水进行比重瓶的检定，这对于含沙量较大水体而言，因水样中溶解质对含沙量的影响比较小，观测人员一般也不会考虑其对含沙量的影响；但当含沙量较小时，水样中溶解质对含沙量的影响就不可忽视，甚至它对含沙量的影响远远大于水体自身的含沙量[1]。所以为了确保含沙量测验的精度，在实际分析工作中，更多用到的是用澄清水进行比重瓶的检定[1,3]。为了提高含沙量测验工作效率，彭世想[4]根据《河流悬移质泥沙测验规范条文说明》[5]中置换法处理泥沙水样“差值法”检定比重瓶的基本原理推导出了一种直接计算得出瓶加清水重的方法，省去了制表、查表环节。但是在推导该方法的过程中，彭世想只考虑了比重瓶的体积膨胀对比重瓶检定的影响，没有考虑清水中存在的溶解质对比重瓶检定的重要影响，所以彭世想推导出来的计算公式只适用于计算比重瓶加蒸馏水或去离子水的情况，对于含有溶解质的澄清水的情况不再适用。为了单独考虑澄清水中的溶解质对比重瓶检定的影响，张海敏[3]通过三门峡站资料进行分析，利用同一温度澄清河水重与蒸馏水重比来确定澄清河水与蒸馏水密度之比与温度之间的关系，这样就避免了水样由于温度变化而引起的体积变化所产生的干扰。认为澄清河水与蒸馏水的密度之比与水温有近似的线性关系，并通过实验资料得出了澄清河水密度与蒸馏水密度之比与水温的相关线性方程，进而求出了澄清河水密度随水温变化的相关表达式。作者对张海敏的表达式进行了校验，发现该表达式与三门峡站实测资料相矛盾，为了探索澄清水中溶解质对水样密度的影响，作者对室温条件下(15～25 ℃)的比重瓶加模型澄清水与比重瓶加蒸馏水的重量分别进行了测验，通过绘制散点图得到模型澄清水密度与蒸馏水密度之比与水温呈现曲线函数关系。基于此，得到了比重瓶法处理水样瓶加澄清水重计算方法，具有较好的实用性。

1 澄清水密度随水温变化规律的探讨

利用清水检定比重瓶的关键问题是确定清水密度随水温变化的规律，当选用蒸馏水或去离子水检定比重瓶时，前人已经给出了较为精确的计算蒸馏水或去离子水密度的计算公式[3,4]。但在实际分析工作中，更多用到的是用澄清水进行比重瓶的检定[1,3]，由于澄清水中溶解质的影响，澄清水密度随温度的变化规律明显不同于蒸馏水或去离子水的密度随温度的变化规律。为了确定澄清水密度随温度的变化规律，张海敏[3]利用三门峡水文站的实验资料进行分析，认为澄清河水与蒸馏水的密度之比与水温有近似的线性关系，得出三门峡站澄清河水密度与蒸馏水密度的相关线性方程：

ρh=ρw(0.002 15T+1.021) (5 ℃≤T≤25 ℃)

(1)

式中：T为水的温度；ρh、ρw分别为相同水温条件下澄清河水和蒸馏水的密度。

为了便于分析计算，张海敏根据Tilton和Taylor提供的实验数据优选率定出了蒸馏水的密度随水温变化的相关方程：

ρw=0.999 995 976-7.313 215 885×10-6(T-4)2

(2)

(0 ℃≤T<8 ℃)

ρw=1.000 104 511-1.695 569 674×10-6T2.346 771 789

(3)

(8 ℃≤T<16 ℃)

ρw=1.000 270 892-4.938 525 939×10-6T2.010 695 513

(4)

(16 ℃≤T<28 ℃)

ρw=1.000 696 372-1.068 671 86×10-5T1.808 782 641

(5)

(28 ℃≤T<30 ℃)

(5)

根据式(1)、(2)、(3)、(4)计算出澄清河水在温度为5～25 ℃时的密度，见图1。可以看出，澄清河水密度计算值随着温度的升高而增大，说明式(1)是单调递增函数。

图1 澄清河水密度计算值随水温关系图Fig.1 Relationship between calculated river water density and temperature

对于物体的体积随温度的改变而引起的变化，通常用物体的体积膨胀系数εv来描述，它表示物体以0 ℃时的体积V0为准，当平均温度升高1 ℃时，单位体积的变化量。设比重瓶在0 ℃时的容积为V0，任一温度时对应的容积为VT，则比重瓶容积随温度变化的函数关系式为：

VT=V0+εvTV0

(6)

显然，式(6)是单调递增函数。则比重瓶内的澄清河水重Wh为：

Wh=ρhVT

(7)

由于ρh、VT均是关于温度变量T的单调递增函数，则比重瓶内澄清河水重Wh必定随着温度T的升高而呈现增大趋势，这与张海敏文中的三门峡站实测资料相矛盾，见图2。

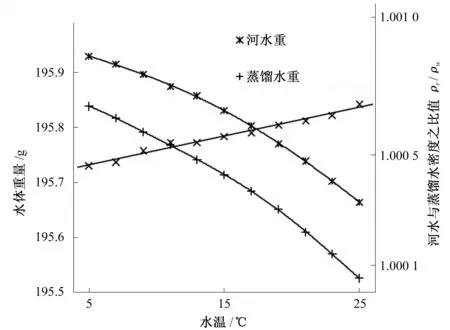
图2 蒸馏水与澄清河水密度之比与水温关系图(三门峡站资料)Fig.2 Relationship between density ratio of distilled water to river water and temperature

对于这种反常现象，对式(2)、(3)、(4)、(5)代入温度数值进行计算，并将计算得到的蒸馏水的密度值与彭世想论文中介绍的西德技术物理研究院蒸馏水密度计算公式[4]得到的蒸馏水密度值进行比较，发现二者吻合良好，说明张海敏率定出的蒸馏水的密度计算公式符合实际情况，因此认为出现上述反常现象是由于张海敏对澄清河水与蒸馏水的密度之比与水温之间近似的线性关系的错误估计造成的，那么澄清水与蒸馏水的密度之比与水温之间究竟存在什么样的关系呢？作者利用某一模型澄清水作了详细的探索。

本实验采用100 mL的比重瓶对模型澄清水和蒸馏水重随温度的变化关系进行了测验。在测验含沙量的过程中，为了避免温度偏离室温过大而引起的比重瓶容积偏离标称容积较大的情况，实际测验过程中一般将水温控制在室温温度上下，所以在本实验中，作者针对温度为15～25 ℃的比重瓶加澄清水与比重瓶加蒸馏水的重量进行了测验。根据规范[6]，本实验中测验比重瓶加水重时对应温度的示值为0.1 ℃。为了保证数据的精度，每一种温度下进行了至少3次以上重量的测验。测验得到的结果见图3，可以看出，模型澄清水与蒸馏水的密度之比随温度的变化并不满足线性关系，而是一种曲线的关系，得到的模型澄清水密度与蒸馏水密度之比随水温变化的拟合曲线方程为：

ρm/ρw=6×10-6T2-2.36×10-4T+1.002 618

(8)

式中：ρm为模型澄清水的密度；ρw为蒸馏水的密度。

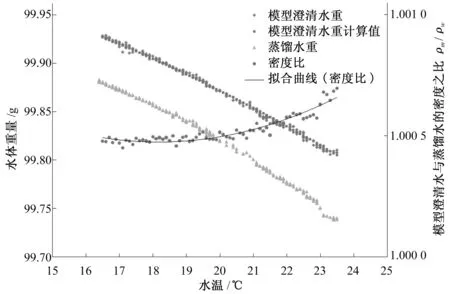
注：图中的模型澄清水计算值是根据后文中论述的比重瓶加澄清水重计算方法计算出来的。图3 蒸馏水与模型澄清水密度之比与水温关系图Fig.3 Relationship between density ratio of distilled water to model clear water and temperature

澄清水不同时，上式中温度变量前的系数也会发生变化，根据上式，任一种澄清水的密度与蒸馏水的密度之比随温度变化的关系为：

(9)

式中：ρcT为温度为T时任一种澄清水的密度。

在实际工作中，欲建立澄清水密度与蒸馏水密度的比值与水温的关系，只需另外称取在测验含沙量水样温度范围内最低温度、中值温度和最高温度3个温度条件下瓶加澄清水与瓶加蒸馏水的重量，代入(9)式即可求出3个常数A、B、C的值，从而建立起澄清水与蒸馏水密度的换算关系。

为了便于计算，选用彭世想[4]论文中介绍的西德技术物理研究院蒸馏水密度值ρw计算公式：

ρw=0.999 839 563 9+6.798 299 989×10-5T-

9.106 025 564×10-6T2+1.005 272 999×10-7T3-

1.126 713 526×10-9T4+6.591 795 606×10-12T5

(10)

根据式(9)、式(10)两式即可得到任一温度下澄清水密度值：

ρcT=ρw(AT2+BT+C)

(11)

2 瓶加澄清水重随温度变化关系式的推导

对于澄清水样的体积随温度的改变而引起的变化，可以用澄清水样的体积膨胀系数εv来描述。它表示澄清水样以零摄氏度时的体积V0为准，当平均温度升高1 ℃时，单位体积的变化量，其表达式可以写成：

(12)

根据式(12)

VT=V0(1+εvT)

(13)

式中：T为温度；VT为温度为T时的澄清水样体积。

当澄清水样温度由T1变化到T2时，其体积相应从VT1变化为VT2，根据式(13)，可将VT2与VT1的关系写成：

(14)

VT2=VT1(1+εvT2)(1-εvT1+ε2vT21-ε3vT31+ε4vT41)

(15)

由于εv值很小，而ε2v值更小，当忽略去ε2v以上高次项以后，得：

VT2=VT1[1+εv(T2-T1)]

(16)

因为

(17)

式中：WT为温度为T时比重瓶内澄清水重；ρcT为温度为T时澄清水的密度。

将它代入式(16)后，得到不同温度时比重瓶内澄清水重关系式：

(18)

式中：WT1、WT2分别为温度为T1、T2时比重瓶内澄清水重；ρcT1、ρcT2分别为温度为T1、T2时澄清水的密度。

若将20 ℃与某一温度T′代入上式，即可写出它们相应的澄清水重关系式为：

(19)

再将某一温度T′与任一温度T代入式(18)，即可写出它们相应的澄清水重关系式为：

(20)

式中：WT′为温度为T′时比重瓶内澄清水重；ρcT′为T′时澄清水的密度；W20为温度为20 ℃时比重瓶内澄清水重；ρc20为温度为20 ℃时澄清水的密度。

式(19)、式(20)相减可得任一温度T与某一温度T′时比重瓶内澄清水重的差值为：

(21)

根据彭世想[4]一文中，εv取为0.000 02；设比重瓶重Wb，上式可写成：

WT+Wb-(WT′+Wb)=

V20[1+0.000 2(T′-20)]{ρcT[1+0.000 02(T-T′)]-ρcT′}

(22)

WT+Wb为任一温度T的比重瓶加澄清水重，写作WbT，WT′+Wb为某一温度T′的比重瓶加澄清水重，写作WbT′。则上式可写成：

WbT=WbT′+V20[1+0.000 02(T′-

20)]{ρcT[1+0.000 02(T-T′)]-ρcT′}

(23)

在实际工作中只需称取在测验含沙量水样温度范围内最低温度、中值温度和最高温度3个温度条件下比重瓶加澄清水与比重瓶加蒸馏水的重量，再根据式(11)、式(23)即可求得任一温度T所对应的比重瓶加清水重WbT。利用此种计算方法计算出来的模型澄清水重随温度的变化规律见图3，可以看出计算的模型澄清水重与测验的模型澄清水重符合很好，说明了此种计算方法的合理性和有效性。

3 结 语

(1)通过对张海敏得到的澄清河水密度与蒸馏水密度之比随温度变化的相关线性方程的分析，发现张海敏公式与三门峡站实测资料相矛盾，进而利用比重瓶对室温情况下(15～25 ℃)模型澄清水和蒸馏水的重量进行了系统地测验，得到了澄清水密度与蒸馏水密度之比随着温度变化呈现曲线函数的关系。

(2)基于澄清水密度与蒸馏水密度之比随温度变化的规律，作者对彭世想推导出来的比重瓶加清水重计算公式进行了改进，以后在实际工作中只需称取在测验含沙量水样温度范围内最低温度、中值温度和最高温度三个温度条件下比重瓶加澄清水与比重瓶加蒸馏水的重量，再根据式(11)、式(23)即可求得任一温度T所对应的比重瓶加澄清水重WbT使得计算公式更方便地用于实际测验含沙量的工作中。

□

[1] 吴彰松，张根广，梁宗祥，等.比重瓶测验低含沙量误差分析[J].长江科学院院报，2016,33(3):5-8.

[2] 蔡守允，朱其俊，张晓红.模型试验含沙量测验仪器的分析研究[J].水资源与水工程学报，2007,18(5):83-85.

[3] 张海敏，李世明，和瑞丽.比重瓶检定方法实验研究[J].泥沙研究，1996,(3):86-91.

[4] 彭世想，沈庆文，李晓伟，等.置换法处理水样瓶加清水重直算法[C]∥中国水利学会第四届青年科技论坛论文集,2008:265-268.

[5] GB50159-92，河流悬移质泥沙测验规范条文说明[S].

[6] SL99-2012，河工模型试验规程[S].